新型黏滞-软钢阻尼器组合系统的概念设计与仿真验证

杨孟刚，胡尚韬，胡仁康，陈政清

(1.中南大学土木工程学院，湖南长沙，410075；2.湖南大学土木工程学院，湖南长沙，410082)

随着飘浮/半飘浮体系大跨度桥梁的不断建设和投入使用，桥梁纵向振动控制的重要性日益凸显。阻尼器作为一种有效的被动控制装置，也越来越多地被应用于大跨度桥梁结构中。目前，桥梁领域应用最广泛的主要有黏滞阻尼器、软钢阻尼器和磁流变阻尼器(MR阻尼器)。

黏滞阻尼器属于速度型阻尼器，在温度及主梁收缩徐变的作用下不会产生阻尼力，在动力荷载作用下能有效耗能，因此，非常适用于大跨度桥梁的纵向减振(震)控制[1]。目前，已有大量学者对黏滞阻尼器在列车、风和地震作用下的减震效果进行了研究[2-5]，结果表明，在大跨度桥梁中，黏滞阻尼器能显著降低结构的动力响应。

软钢阻尼器最初是作为一种被动振控装置提出的，主要应用于建筑领域[6]和梁桥的减震控制[7]，在大跨度桥梁的横向减震方面也有少量研究[8]。在大跨度桥梁纵向减震方面，仅有个别学者进行了仿真分析。WANG 等[9]和张玉平等[10]分别对1 座单塔悬索桥和1座三塔悬索桥进行了软钢阻尼器的减震分析，结果表明软钢阻尼器在抵抗大地震时效果显著。

MR阻尼器具有能耗少、响应速度快、阻尼力连续顺逆可调等优点，已在斜拉桥拉索减振、高层建筑振控等领域有所应用[11]。部分学者也在大跨度桥梁的纵向减振(震)方面对MR阻尼器进行了研究。杨孟刚等[12-13]以自锚式悬索桥为对象研究了MR 阻尼器在车辆制动力及地震作用下的减振(震)效果，发现MR阻尼器对结构振(震)动控制效果显著。秦顺全等[14]对MR阻尼器和黏滞阻尼器混合系统进行了研究，验证了MR阻尼器对列车制动力的控制效果。

但是，在大跨度桥梁纵向单独使用黏滞阻尼器、软钢阻尼器或MR阻尼器均存在一些不足。对于黏滞阻尼器，漏油和失效的情况在大质量阻尼器中时有发生[15-16]，且由于黏滞阻尼器给桥梁提供的附加阻尼比与阻尼器质量呈非线性关系[17]，抵御大地震需要更大的阻尼力和更大质量的阻尼器，这不经济。对于软钢阻尼器，由于其必须在大位移的情况下才能发挥强大的耗能能力，但在温度、风和制动力作用下会对结构产生不利的附加力。此外，为抵御大地震所设计的MR阻尼器具有与软钢阻尼器相似的特性，仍然难于满足温度作用下的需求。

综上所述，本文作者提出一种适用于大跨度桥梁纵向减振(震)的黏滞-软钢阻尼器组合系统，并进行仿真分析。该系统利用黏滞阻尼器抵抗温度、风、列车荷载及小地震作用，利用软钢阻尼器抵御大地震作用。以我国某特大铁路悬索桥设计方案为例，合理选取组合系统中黏滞阻尼器和软钢阻尼器的设计参数，并分别对两者的减振(震)效果进行仿真验证，最后探究组合系统的减振(震)效果以及锁定延时效应，旨在为黏滞-软钢阻尼器组合系统的开发与应用提供理论基础。

1 黏滞-软钢阻尼器组合系统机理

黏滞-软钢阻尼器组合系统的简化模型如图1所示。组合系统由黏滞阻尼器、外接机械锁定装置以及软钢阻尼器三者串联而成，可以根据不同的桥梁构造安装在主梁与承台或桥台之间。黏滞阻尼器一端与主梁铰接，另一端通过锁定装置与软钢阻尼器相连，而软钢阻尼器与桥台或者承台固结。组合系统的工作流程图如图2 所示。在温度、列车、风以及小地震的作用下，当黏滞阻尼器活塞杆出力Nv小于锁定力Nl时，锁定装置未锁定，黏滞阻尼器活塞杆可以自由运动，此时，黏滞阻尼器处于正常工作状态。而软钢阻尼器由于具有较大的初始刚度，在黏滞阻尼器阻尼力作用下并未屈服，可视为具有一定刚度的固定端。此阶段黏滞阻尼器工作，软钢阻尼器不工作。在大地震作用下，当黏滞阻尼器活塞杆出力Nv大于锁定力Nl时，锁定装置锁定，黏滞阻尼器活塞杆不再受力，因此退出工作，此时，整个黏滞阻尼器相当于一根刚性连杆，将软钢阻尼器直接与主梁相连，软钢阻尼器超过屈服位移，并开始滞回耗能。地震结束后，人工复原锁定装置即可，黏滞阻尼器和软钢阻尼器并未受到破坏。

图1 黏滞-软钢阻尼器组合系统的简化模型Fig.1 Simplified model of combined system of viscous and steel dampers

图2 黏滞-软钢阻尼器组合系统工作流程图Fig.2 Working procedure flowchart of combined system of viscous and steel dampers

在组合系统中，黏滞阻尼器和软钢阻尼器的参数需要具有良好的适配性，才能保证二者的协同工作性能。对于黏滞阻尼器，通过对不同参数组合的黏滞阻尼器在小地震作用下的减震效果进行时程分析，选出最优参数；对于软钢阻尼器，基于黏滞阻尼器参数，对其进行理论公式推导及有限元实体模型验证，并对该参数软钢阻尼器减震效果进行验证，从而确定软钢阻尼器的设计参数。最后，将黏滞阻尼器最大出力设置为锁定力，并将黏滞阻尼器和软钢阻尼器的参数进行组合，得到组合系统的参数。

2 工程背景与模型建立

采用我国某特大铁路悬索桥设计方案作为工程背景进行分析研究。该大桥为铁路钢桁架空间索面悬索桥，主缆跨度为(245+1060+270) m，主梁跨度为(90+1060+130)m，采用隧道锚结构，双线铁路桥，全桥总长1 292.5 m。主塔为钢筋混凝土结构，根据两岸地形，主塔采用高、低塔结构型式。高塔由上、下塔柱及上、下横梁4 部分组成，塔高255.8 m；矮塔由上塔柱及上横梁两部分组成，塔高145.8 m。主塔截面采用空心矩形截面。主梁采用上承式钢桁梁，华伦式桁架，桁高为12 m，节间为10 m，主桁中心距为30 m。主缆采用预制平行钢丝索股(PPWS)，吊索纵向标准间距10 m，横向间距48 m。桥塔基础采用分离式承台。总体结构体系为塔梁分离、塔墩固结形式，塔梁之间设置横向及竖向支座。悬索桥的桥型图如图3所示。

图3 悬索桥的桥型图Fig.3 Diagram of suspension bridge

采用有限元分析软件ANSYS 建立悬索桥模型。其中，主梁、主塔和承台采用BEAM4单元模拟，主缆和吊索采用LINK10单元模拟，基础桩土效应采用“m”法计算并通过MATRIX27单元输入模型中，竖向和横向支座分别采用COMBIN14 和COMBIN39 模拟。模型中，忽略主梁上的铁路纵梁和索鞍细部构造，桥台直接当作固结处理。桥梁模型如图4所示。

图4 悬索桥有限元模型Fig.4 Finite element model of suspension bridge

利用子空间迭代法对悬索桥模型进行模态分析，前10阶成桥状态动力特性如表1所示。由表1可知：该桥一阶频率为横弯，这是由于该悬索桥为双线铁路桥，主梁宽度较小，因此，横向刚度较小。在本文中，由于研究对象为大跨度桥梁的纵向减震，因此，更应该注意的是纵飘振型所对应的自振频率即二阶频率，为0.085 47 Hz。总体上，该悬索桥的动力特性符合一般悬索桥动力特性。

表1 悬索桥动力特性Table 1 Dynamic characteristics of suspension bridge

3 动力荷载及地震动输入

3.1 动力荷载

对于大跨度铁路桥梁纵向振动而言，需要考虑的动力荷载主要包括列车行车荷载、制动力及脉动风荷载。

图5 所示为动力荷载。列车行车荷载考虑HXD2型电力机车，轴重为250 kN，共16 节车厢，以最大速度120 km/h 在主梁上匀速行驶，考虑由车头上桥到车尾下桥的全过程。列车轴重如图5(a)所示。图5(b)所示为第1 节车厢的制动时程曲线，其他15节车厢的制动时程曲线与之基本重合。

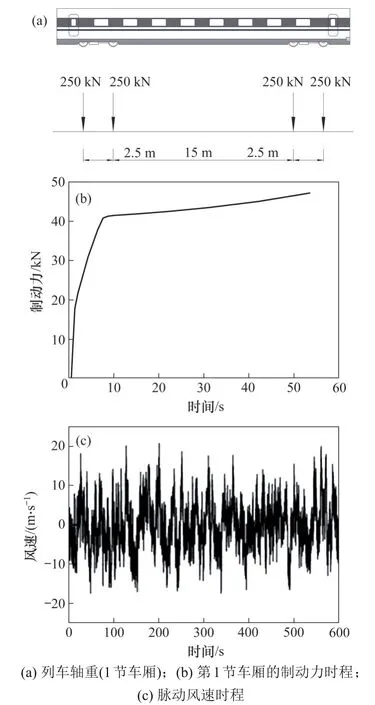
图5 动力荷载Fig.5 Dynamic loads

考虑列车制动力紧急制动情况下，由机车踏面制动提供的制动力作用，16 节车厢均提供制动力。考虑制动开始到列车停止的全过程，包括制动力消失后主梁的振荡效应。制动力时程如图5(b)所示。

脉动风采用Davenport 风速谱，利用谐波叠加法求解单点脉动风速，利用伯努利方程换算成风压后平均施加到主梁横截面节点上。脉动风速时程如图5(c)所示。

3.2 地震动输入

本文中悬索桥采用两水准抗震设计，根据相关工程场地地震安全性评价报告，具体计算采用：E1 地震作用(水准I)地表峰值加速度为0.28g(1g=9.806 65 m/s2)，特征周期为0.6 s；E2 地震作用(水准II)地表峰值加速度为0.56g，特征周期为0.7 s。根据峰值加速度及场地特征周期，获得两水准下的反应谱曲线，根据该反应谱，利用SeismoArtif软件模拟3条人工波，将这3条波均调幅至峰值加速度(PGA)为0.28g，时间取前40 s。地震波加速度时程如图6所示。

图6 人工地震波加速度时程Fig.6 Acceleration time history curves of artificial waves

4 组合系统参数确定

4.1 黏滞阻尼器参数确定与减振(震)分析

对于黏滞阻尼器而言，力与速度的关系为

式中：C为阻尼系数；v为活塞杆纵向速度；α为速度指数。对于实桥中所设置的黏滞阻尼器，还需要考虑黏滞阻尼器的数量以及安装位置。

采用参数组合穷举法来获得黏滞阻尼器最佳参数组合[18-20]。由于桥梁结构各阻尼器并联工作，在阻尼器数量不定，速度指数一定的前提下，定义桥梁黏滞阻尼器总阻尼系数Ctotal=nC(其中，n为数量)，则确定最佳总阻尼系数和速度指数组合后，可以进一步求出阻尼器数量和单个黏滞阻尼器阻尼系数。表2所示为部分实际工程和研究中所使用的黏滞阻尼器参数。从表2 可知：C通常为2～10 MN·(s/m)α，α通常为0.2～1.0。最终在穷举法中，取总阻尼系数Ctotal为24，36，48，60，72，96 和120 MN·(s/m)α，速度指数α为0.2，0.3，0.4，0.5，0.6，0.8 和1.0，共49 种组合。考虑到该悬索桥矮塔的构造为主梁直接架在承台上，缺少横梁以安装阻尼器，因此，将黏滞阻尼器安装在桥台上。

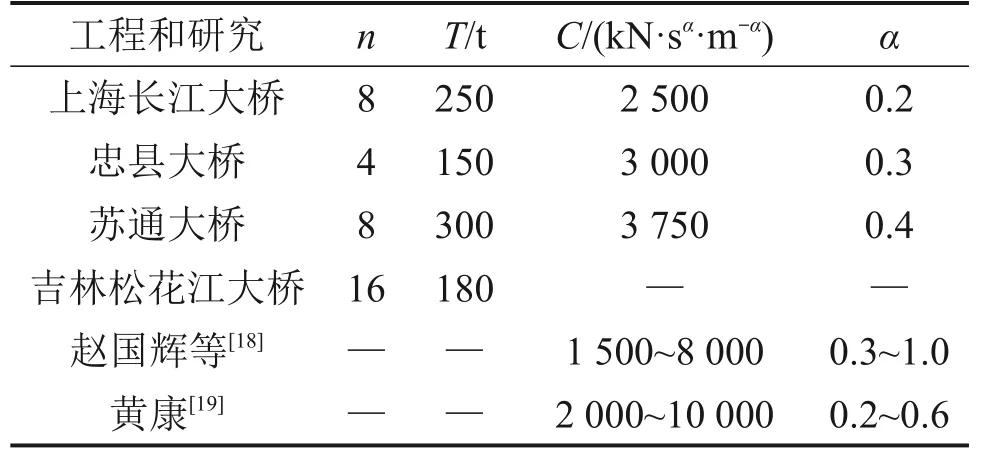
表2 实际工程和研究中使用的黏滞阻尼器参数Table 2 Parameters of viscous dampers applied in bridge projects and research

在全桥模型中，利用COMBIN 37 单元模拟黏滞阻尼器，对E1 地震(0.28g)作用下结构响应进行时程分析。图7所示为不同参数组合的黏滞阻尼器对结构响应的影响结果。由图7可知：随着阻尼系数增大和速度指数减小，梁端纵向位移显著减小，阻尼器出力显著增大，高塔和矮塔塔底内力逐渐增大，但总体上变化不大。考虑到本系统的目标是避免大质量阻尼器的使用，综合表2中实际工程所使用的的阻尼器参数，将黏滞阻尼器质量T限制在150 t 及以下，数量n限制在8～16 个。最终选取阻尼器的阻尼系数C=2 250 kN·(s/m)α，速度指数α=0.4，数量n为16个，黏滞阻尼器质量T为150 t。在此参数下，黏滞阻尼器减振(震)率见表3。从表3可以看出：安装黏滞阻尼器后，列车及风荷载作用下主梁位移减震率均超过80%；地震作用下主梁位移减小了64.0%，塔底弯矩最高减小了9.0%，塔底剪力最高减小了9.9%。计算结果表明黏滞阻尼器抵抗列车、风及小地震的效果良好。

表3 黏滞阻尼器减振(震)效果Table 3 Vibration reduction effect of viscous dampers

图7 黏滞阻尼器不同参数组合对结构响应的影响Fig.7 Effect of different viscous damper parameter combinations on structural maximum responses

4.2 软钢阻尼器参数确定与减震分析

目前桥梁用软钢阻尼器主要有3种形式：减震榫、E 形钢阻尼器和X 形(三角形)钢阻尼器。考虑到减震榫同时具备比较强的出力能力和位移能力[20]，因此，选取矩形减震榫作为软钢阻尼器参数设计的基础形式，多根减震榫并联组成软钢阻尼器。为简化减震榫的细部参数设计，取1根钢榫进行计算，其力学模型可以简化为一个变截面悬臂梁，如图8(a)和8(b)所示。其中，d1，d2和d3分别为减震榫顶部、中部过渡段和底部的宽度；h0为减震榫直线段高度；h为减震榫总高度；b0为减震榫厚度。

图8 减震榫模型Fig.8 Simplified model of damping tenon

当减震榫截面外缘应力达到材料屈服强度时，认为钢棒进入屈服。令材料屈服强度为[σ]，可得减震榫屈服力Fy为

根据力法和图乘法求得钢榫初始柔度δ为

根据屈服力和初始刚度可以得到屈服位移Δy为

根据4.1节得到的黏滞阻尼器参数，可以初步确定软钢阻尼器屈服力应略大于1 500 kN。考虑到E2地震PGA达到0.56g，地震作用下主梁纵向位移较大，初步确定软钢阻尼器极限位移为300 mm。基于此，可以得到单根减震榫尺寸参数见表4。本系统单个软钢阻尼器所用减震榫数为24根。

表4 单根减震榫设计参数Table 4 Design parameters of damping tenon

为了验证理论计算的准确性，利用ANSYS 建立单根减震榫实体模型，如图8(c)所示。对模型进行位移滞回加载，可以得到减震榫的滞回曲线。减震榫在位移为50，100，200和300 mm时的滞回曲线如图9所示。由图9可知：减震榫滞回曲线饱满，耗能能力强，极限位移大，适合于大跨度桥梁纵向减震。将减震榫参数理论计算结果与仿真结果进行对比，结果见表5。由表5 可知：减震榫参数理论计算与有限元实体模型所得参数相对误差均在10%以内，说明理论计算精度较高。最终可确定软钢阻尼器屈服力为1 626 kN，初始刚度为78 013 N/mm，屈服位移为20.85 mm，极限位移为300 mm。

表5 单根减震榫理论与仿真结果对比Table 5 Comparison of a single tenon’s mechanical parameters obtained by theoretical value and FE model

图9 单根减震榫滞回曲线Fig.9 Hysteresis curve of damping tenon

根据理论及仿真结果，对软钢阻尼器在全桥中的减震效果进行有限元时程分析。利用COMBIN 40 单元模拟软钢阻尼器力与位移曲线的双线性特性。由于本系统旨在利用软钢阻尼器在黏滞阻尼器锁定后迅速进入工作状态，需要软钢阻尼器在E1 以上各级别地震中都能屈服，并具有良好的减震效果，因此，分别对峰值加速度(PGA)为0.35g，0.42g，0.49g和0.56g的地震作用进行计算，结果如图10 所示。由图10(a)～(d)可知：软钢阻尼器对桥塔内力有一定的减弱效果，塔底弯矩减震率为3.7%～20.5%，塔底剪力减震率为0.3%～12.9%。由图10(e)可知：软钢阻尼器能够很好地控制结构在大地震作用下的位移，位移减震率为70.0%～77.6%。从图10(f)可以看出：软钢阻尼器在E2 地震下滞回曲线饱满，最大位移达到291 mm，充分发挥了其耗能能力。计算结果表明软钢阻尼器抵抗大地震的效果良好。

图10 软钢阻尼器减震效果Fig.10 Vibration reduction effect of steel dampers

5 组合系统减振(震)分析

5.1 组合系统单元的简化模拟

在组合系统中，工作流程可以简化为：在列车、风及小地震作用下，仅黏滞阻尼器工作，软钢阻尼器处于弹性状态，相当于黏滞阻尼器和线性弹簧串联，线性弹簧的刚度相当于软钢阻尼器初始刚度；在大地震作用下，仅软钢阻尼器工作。在ANSYS中，这种串联模式可以通过并联形式模拟，并通过改变单元的边界条件达到锁定的目的。即单元连接固定支座时视为处于工作状态，单元连接可动支座时视为退出工作状态。

单元模拟示意图如图11所示。其中，单元I为黏滞阻尼器单元，用COMBIN 37 单元模拟；单元II 为软钢阻尼器初始刚度单元，用COMBIN 14 单元模拟；单元III 为软钢阻尼器单元，用COMBIN 40 单元模拟。单元组中，单元I 和单元II 相串联，单元II 后接支座；单元III 后接支座和单元I、II 串联系统并联。在列车、风及小地震作用下，锁定装置未锁定，此时，单元II 后接固定支座，单元III后接纵向可动支座，相当于单元I和II串联系统正常工作，而单元III 不工作；在大地震作用下，锁定装置锁定，此时，单元II后接纵向可动支座，单元III后接固定支座，相当于单元I和II串联系统退出工作，而单元III 开始工作。通过改变并联系统中每个单元的边界条件，可以有效实现组合系统的既定功能。

图11 组合系统单元的简化模拟Fig.11 Simplified simulation of combined system

5.2 组合系统减振（震）分析

对组合系统在各种动力荷载作用下结构响应的控制效果进行分析。图12 所示为各种动力荷载作用下主梁位移时程曲线，表6 所示为0.28g和0.56g地震作用下组合系统对结构内力的控制效果。由图12 可知：在列车行车荷载、制动力以及风荷载作用下，组合系统减振率分别达到了84.8%，88.0%和69.6%；在不同PGA的地震作用下，主梁位移减震率最高可达73.9%，桥塔弯矩减震率最高可达11.3%，桥塔剪力减震率最高可达13.2%。由图12(d)可知：锁定装置在0.28g地震作用下未锁定，仅黏滞阻尼器起作用。由图12(g)和(h)可知：在大地震作用下，锁定装置在黏滞阻尼器第1次到达锁定速度时锁定，随后软钢阻尼器开始耗能。锁定时间tlock随着PGA 的增大而提前，这是因为PGA 越大，黏滞阻尼器出力越大，越早达到锁定力，从而被锁定。计算结果充分说明组合系统可以实现锁定，并有效抵御各种动力荷载引起的桥梁振(震)动。

表6 组合系统对结构内力减震效果Table 6 Reduction effect of combined system on structural internal forces

图12 组合系统对主梁位移减振(震)效果Fig.12 Reduction effect of combined system on girder’s displacement

5.3 锁定延时效应的影响

本文所提出的黏滞-软钢阻尼器组合系统使用外部机械装置实现锁定，由于实际加工和使用中装置各部分配合，在锁定过程中势必会产生延时现象，此时，黏滞阻尼器已经退出工作，而软钢阻尼器还未进入工作状态，桥梁相当于进入未保护状态。机械装置配合程度越低，延迟时间越长。而考虑到锁定时黏滞阻尼器已达到最大速度，意味着主梁也达到最大速度，因此，延时效应会对主梁位移会产生较大影响。为了考虑延时效应对黏滞-软钢阻尼器系统减震效果的影响，为阻尼器系统的良好协同工作性能提供理论保障，选取无延迟(延迟0 s)、延迟0.1 s、延迟0.2 s 和延迟0.3 s共4个工况进行计算。为了直观地看出延迟时间对主梁位移的影响，仅选取1 条人工波，即人工波1进行计算。为了研究不同等级地震下延时效应的影响，依旧选取PGA 为0.35g，0.42g，0.49g和0.56g进行时程分析，结果如图13所示。

从图13 可以看出：延迟时间对锁定后时程曲线形状变化不大，但是曲线整体发生偏移，偏移量即为锁定延迟期间主梁在不受限制情况下的位移。延时越长，偏移量越大。在PGA 为0.35g和0.42g的地震作用下，主梁最大位移发生在锁定前的黏滞阻尼器工作阶段，锁定延时造成的偏移没有对最大位移产生贡献。在PGA为0.49g的地震作用下，主梁最大位移发生在锁定后的软钢阻尼器工作阶段，锁定延时对最大位移造成较大影响，延时越长，偏移量越大。不考虑延时效应时，主梁最大位移为276 mm；延时0.3 s时，主梁最大位移为294 mm，偏移量为18 mm。在PGA 为0.56g的地震作用下，由于主梁最大位移发生的方向与锁定延时产生的偏移量的方向相反，锁定延时反而对总体减震产生有利效果。不考虑延时效应时，主梁最大位移为324 mm；延时0.3 s时，主梁最大位移为244 mm，偏移量为80 mm。本文为了突出比较效果，仅选用1条人工波进行计算。在实际工程中，由于地震波的随机性，锁定延时造成的偏移方向是无法预测的，总体来看，对确定结构的减震策略和减震效果不利。此外，对于外接机械锁定装置而言，锁定延时越长，对锁定装置的位移容许量也提出更高要求。因此，严格控制锁定装置的设计和加工精度，减小锁定延时，对保证黏滞-软钢阻尼器组合系统的整体稳定性和有效性很有必要。

图13 不同延时对主梁位移的影响Fig.13 Influence of different delay times on girder’s displacement

6 结论

1)黏滞-软钢阻尼器组合系统利用小质量黏滞阻尼器满足温度、风、列车制动力和行车荷载以及小地震作用下的需求，利用软钢阻尼器抵御大地震作用，不仅解决了单独使用大吨位黏滞阻尼器的有效性和经济性问题，而且克服了软钢阻尼器在温度、风、列车制动力等作用下的局限性，扩展了其应用范围。

2)黏滞阻尼器可以有效控制脉动风、列车制动力、列车行车荷载、小地震等作用下的结构响应，其中位移减振(震)率超过64%；软钢阻尼器可使大地震下的位移响应减小70%以上；组合系统较好地实现了由黏滞阻尼器工作状态至软钢阻尼器工作状态的锁定转换控制。

3)组合系统的锁定延时会使主梁位移产生一定量的偏移，延时越长，偏移量越大，对减震设计不利，因此，在实际设计时，应缩减锁定装置的延时时间，尽量避免或减小组合系统的锁定延时效应。