“x=5”是不是方程？

周佳泉

【编者按】 数学是严谨的科学。在大部分人的心目中，数学“一是一，二是二”。但在实际的教学中，我们常常遇到一些数学问题似乎难有定论。从本期开始，我们将开辟“牛角尖里的数学”专栏，选取一线教师们普遍关心的“有争议”的问题，为大家提供一个交流、借鉴的平台，以期对小学数学教学中“有争议”的问题达成一个比较清晰的共识，也欢迎大家提问共讨。

“x=5”是不是方程？这是一线教师们经常争论的一个问题。本人认为，对这个问题要进行分类讨论：

一、从方程的文字定义来说

根据现行人教版小学数学教材对方程的文字定义“含有未知数的等式，叫作方程”来说，“x=5”绝对算是一个方程。因为它符合方程定义的两个要素——首先它是等式，其次含有未知数“x”。

二、从方程的功能价值来说

如果基于“方程是在未知量与已知量之间建立等量关系，从而求得问题解决的一种思维工具”的功能价值来说，“x=5”算不上是一个真正的方程。原因有两个：一是这个方程没有任何实用价值（它不能解决任何实际問题）;二是未知数“x”的值已经确定（就是5），“x”已经不是真正的未知数了（这就好比甲问乙：“张老师，请问您贵姓？”）。

三、从解析几何的表达式来说

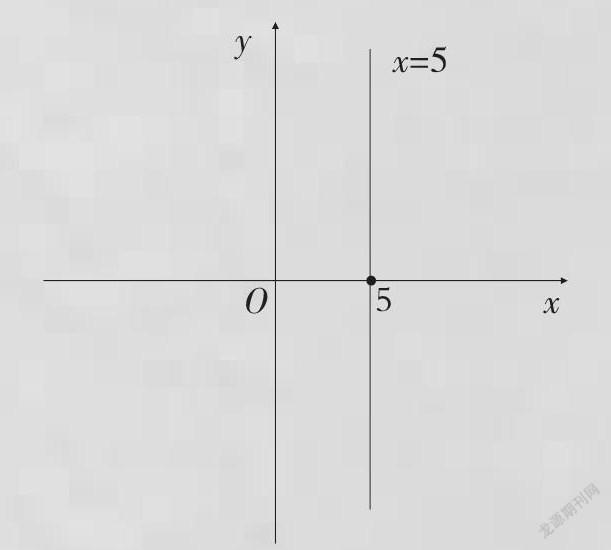
如果从解析几何的表达式来说，“x=5”确确实实是一个方程。它描述的是在平面直角坐标系中通过“x=5”这个点，并且平行于轴的直线（如下图）。

启示：

1.思考问题从目标切入才更有价值。比如我们讨论“‘x=5’是不是方程？”这个问题之前，恐怕我们更应该先反问自己：“判断‘x=5’是不是方程，我们的目的是什么？”

2.摒弃二元思维才能对问题达到全面理解。长期从事一线小学数学教学的工作，容易让人形成“严谨有余，变通不足”的思维定式，尤其容易落入“非此即彼，不对就错”的二元思维窠臼之中。“分类讨论”是消除二元思维局限性的良好思维方法，值得我们大家借鉴。