高速列车运行时隧道内漏缆卡具的气动效应

程 梦，曹从咏，龚 振，姚鑫苗

(南京理工大学 自动化学院，南京 210000)

高速列车在隧道半封闭环境内运行时，产生的列车风与隧道壁面相互耦合，造成隧道内流场剧烈扰动，会对漏缆卡具造成气动冲击作用，进而有可能使漏缆固定卡具损坏或脱落，导致漏缆无法固定，危及行车安全。因此，研究列车运行时对漏缆卡具的气动冲击有很重要的意义。

对于高速列车运行产生的气动效应，国内外不少学者对其展开了大量的研究。针对列车在隧道内行驶时的工况，Howea等[1]学者多年来致力于研究列车在通过隧道内产生的压缩波现象，其团队建立了用于计算车头进隧道时产生压缩波的分析模型，证明当车鼻驶入隧道时，喷出的大涡流对隧道压缩波的贡献很小，这一现象与人们先前的认知相悖。Rezvani等[2]通过数值模拟的方法研究高速列车在横风条件下的稳定性，并证明了湍流模型在研究列车气动问题上的可行性。Sakuma等[3-6]通过测量隧道内高速列车运行时的风速和压力波动，研究相干结构及其在列车横截面周长上的分布规律。Masahiro等[7]研究了列车在不同隧道结构行驶时的气动压力差异。Rabani等[8]对高速列车驶入隧道过程中的压缩波进行了研究。马东宝[9]利用湍流模型，研究了时速磁悬浮列车以500 km/h的速度通过隧道时绕流流场的压力波特性，得到隧道压力波中的压缩波使流场压力升高，膨胀波反之。梅元贵[10]对货运列车在隧道内运行时的压力波现象进行过深入研究，定量分析装载门的凹陷对于列车绕流流场压力波特性的影响。于淼等[11]通过数值模拟方法对列车车体和底部部件进行列车气动特性细化分析，并根据分析提出有效的气动优化方案；牛纪强[12]采用数值计算方法,对不同编组长度高速列车以不同速度通过隧道时产生的列车风进行研究。然而针对列车运行时隧道内设备的气动效应研究还不多，有待于深入展开研究。

以隧道内漏缆卡具为对象，采用CFD数值模拟方法研究隧道内列车风对卡具的气动冲击效应；建立高速列车绕流流动的数学模型，考虑到列车的运动的影响，采用动网格技术进行网格重构；数值模拟获得高速列车通过时隧道内漏缆卡具的气动冲击特性，为卡具疲劳分析及结构优化设计提供参考。

1 列车绕流流动数学模型

1.1 控制方程

在笛卡尔坐标系下，可用积分形式的三维可压缩雷诺平均Navier—Stokes方程来描述高速列车绕流流动[13]：

(1)

(2)

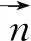
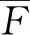
(3)

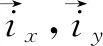
选取标准k-ε湍流模型[14]进行求解，其湍流动能k耗散率ε方程如下：

(4)

(5)

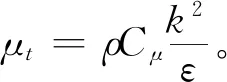
1.2 控制方程的离散

在建立好湍流模型之后，对求解区域进行离散化处理，常用的离散方法有:有限差分法、有限元法以及有限体积法等[15]。本文均采用有限体积法对高速列车流场的控制方程进行求解。

对任意的控制体积V，这里考虑任一标量φ的积分控制方程：

(6)

式中，ρ为密度，A为控制单元表面积，Γφ为φ的扩散效率，▽φ为φ的梯度，Sφ为单位体积内φ的生成。

在给定的网格上，采用FVM对式(6)进行离散后，方程变为：

(7)

式中，N为相邻网格面的数目，φf为通过面f的φ对流量，uf为通过面f的质量流速，Af为面f的面积，(▽φ)n为▽φ沿面f法线方向的大小，V为网格体积。

经离散后的方程可以写成如下通用公式：

apφ=∑nbanbφnb+b

(8)

其中，ap为离散方程φ的系数，anb为离散方程φnb的系数，b是离散方程的源项。下标nb表示相邻的网格。

对控制方程进行离散将微分方程转化成代数方程，简化求解方式，最后确定边界条件，按式(8)求解获得流场的分布。

2 几何模型与计算区域

为模拟列车在运行过程中列车风对卡具的影响，需分别建立列车组，隧道及漏缆卡具的几何模型。

2.1 高速列车的几何模型

以CRH380A型列车为研究对象，采用“头车+中间车+尾车”的三节编组形式[16]，如图1所示，头车和尾车长26.25 m(包括了12.00 m长的流线部分)；中间车长24.50 m；连接各节车厢的风挡长0.50 m；列车整体宽3.38 m，高3.70 m。

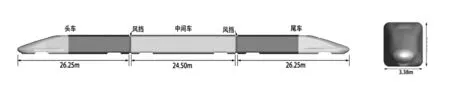
a:侧视图 b:正视图

2.2 隧道与漏缆卡具的几何模型

首先建立隧道的几何模型，参照《高速铁路设计规范》(TB10621-2014)[17]，进行一定程度的简化，忽略隧道内竖井、导流孔等结构，建立单洞双线隧道，隧道端口处截面如图2所示。同理，漏缆卡具尺寸相对于列车及隧道尺寸来说很小，因而对其进行一定程度简化，漏缆卡具模型如图3。

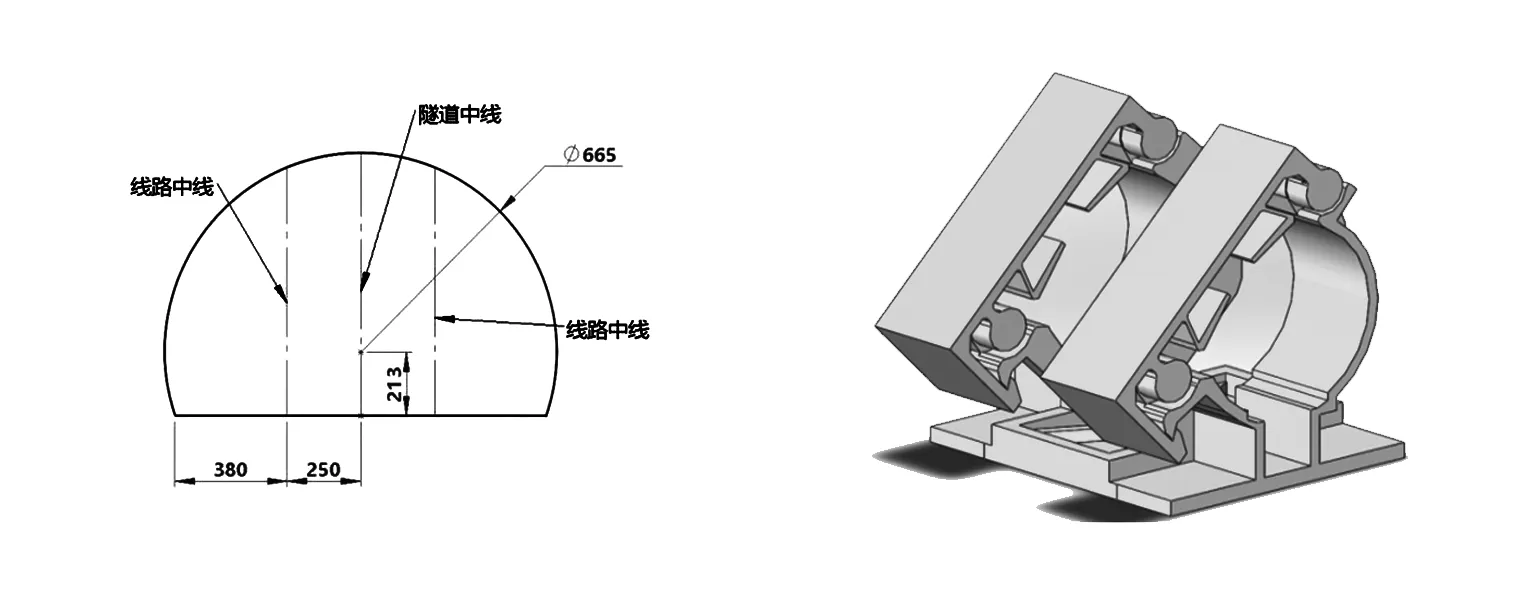
图2 隧道截面示意图 图3 卡具三维图

2.3 计算区域的划分

所计算的区域为600 m的隧道及隧道向两边延伸尺寸为200 m长半径为80 m半圆柱空气场区域，如图4所示；头车鼻尖所在位置为坐标原点，列车轴线为x轴。

a:整体计算区域示意图

考虑到隧道不同位置处流场差异性较大，为探究不同位置处卡具气动冲击特性的差异性，本文共考虑了3组卡具，如图5所示，每组卡具含两个距轨面高度分别为2.2 m和4.6 m的卡具；3组卡具放置在列车前进方向的右侧，第一组位于距离隧道入口1 m的位置，第二组位于隧道中间段，第三组位于距离隧道出口处1 m的位置。

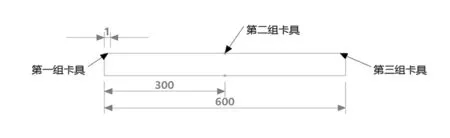
图5 漏缆卡具安放位置示意图(长度/m)

3 网格生成

在研究列车运行产生的气动效应时，需采用动网格技术[18]模拟列车的运动，通过对网格进行重构以保证迭代计算的进行。本文采用铺层法进行网格重构，该方法中需要将计算域分为动域和静域，两个区域之间建立滑移交界面完成数据传递；在运动边界上设置一个最佳网格高度，当结构体运动导致临近边界的网格高度与设置的最佳网格比例过大时，则插入一层网格，反之，则销毁一层网格。划分静域与动域后列车周围网格纵断面见图6。

图6 列车周围网格纵断面图

隧道区域的网格在划分了动域和静域后，对静域采用多层嵌套O型网格处理隧道壁面、计算域边界等圆弧界面处的网格扭曲，并且由轴线至母线网格逐渐稀疏，以节约网格数量缩短计算时间。隧道的外围流场生成的网格如图7所示。

在完成背景网格的划分后，对组件区域进行网格划分，漏缆卡具的网格划分结果如图8。

图8 漏缆卡具表面网格

4 边界条件处理

边界条件是指在求解区域的边界上所求解的变量或其一阶导数随时间、空间的变化规律，不当的边界条件常常会造成计算发散或者仿真结果不合理的现象。合理的边界条件才能保证计算过程的可行性，才能得到正确计算结果。因此，对高速列车绕流流场的模拟需要设定合理的边界条件。

由于采用动网格技术模拟列车通过隧道真实过程，计算域的边界条件较为复杂，结合图9，边界设置如表1所示。

表1 边界条件设置表

a:地面区域计算边界编号

隧道两端的半圆柱空气域边界为压力出口，回流压力为101 325 Pa；隧道壁面、地面、设置为静止的壁面类型[19]；轨道下方地面为运动壁面[20]。

对于模拟列车运动所采用的动网格技术，利用动态层法来更新列车运动导致的网格变形区的体网格。该方法主要是根据静止边界网格附近相邻网格尺寸变化添加或减少网格层，适用于单一方向上的边界运动。针对高速列车通过隧道时的绕流流场特性和列车方向性较强特性，选择动态层法解决高速列车运行产生的网格形变问题。

5 数值模拟

本文采用CFD数值模拟方法，研究不同列车运行速度下列车风对泄漏电缆及卡具施加的表面压力、横向力(X方向)、纵向力(Z方向)、升力(Y方向)特性。

5.1 计算工况

计算初始条件设置为：计算域内初始压力为一个标准大气压，初始温度为298 K。其计算工况见表2。

表2 计算工况

5.2 卡具表面压力特性

上文提及计算域内隧道壁面上布置3组卡具，从漏缆卡具气动力分析来看，3组卡具表面压力特性相似，且安装于中部的一组卡具所承受的表面压力值较大，更能反映列车不同运行速度下漏缆卡具表面压力变化规律，因此下文仅探讨该组卡具。在不同速度下，隧道中部卡具所受表面压力变化情况见图10。列车以500 km/h行驶时中部卡具的表面压力正峰值比350 km/h行驶时的列车早出现0.5 s左右；而负峰值则早出现0.75 s。

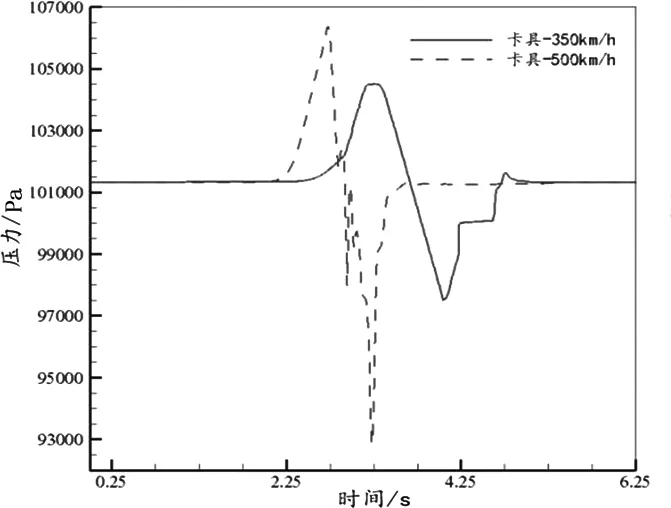
图10 不同速度下中部卡具所受表面压力

表3给出的是隧道中部漏缆卡具表面压力的正负峰值随列车速度改变的增加值。当列车车速从350 km/h提高到500 km/h时，卡具表面压力负峰值增量较大为4662 Pa，正峰值增量为1859 Pa。

总得来说，当列车不同速度通过隧道的中部漏缆卡具时，卡具所受表面压力的是随着列车速度的提高而有着明显的增加的；列车以500 km/h的速度通过隧道中部卡具时，漏缆卡具的峰值增量有明显的增加；当列车运行速度由300 km/h提升到500 km/h时，同一位置卡具所受压力波到达时间提前。

5.3 横向力

通过对漏缆卡具表面压力的数值模拟结果可知，列车以500 km/h的速度通过隧道时，为本文所研究的极端工况，为简化数值模拟工作量，下文仅对对极端工况2的结果进行分析。列车运行速度为500 km/h时，隧道内不同位置及不同高度的横向力变化曲线见图11。

a:高度2.2 m b:高度4.6 m

图11中数据显示：当列车通过隧道时，卡具的横向力曲线存在两个峰值，随着列车靠近，卡具一开始受到车头压缩波影响有靠近隧道壁面的运动趋势；列车经过时，卡具位于车身与隧道壁面形成的环状流场中，受列车风的影响受力曲线不断振荡；当列车经过后，卡具处于车尾负压区，再次有远离隧道壁面、被拔出的运动趋势，随着列车不断通过隧道，卡具横向受力不断变化，形成振荡。

由表4可知位于高度2.2 m、隧道中点处卡具横向力正、负峰值最大，仿真结果分别为10.05 N、-10.95 N。

表4 工况2卡具横向力峰值表 N

总体来说，高度为2.2 m的卡具横向力大于高度4.6 m的卡具，两者横向力曲线相似，但2.2 m处卡具正负峰值均大于4.6 m处卡具，这是因为2.2 m处卡具距离车头鼻尖位置更加接近，因此受到的横向力数值较大。位于隧道中点处的卡具横向力正、负峰值都较大，位于隧道出口处的卡具次之，分析原因在于，隧道中点处卡具绕流流场受限程度最高，流场压力变化最为剧烈。

5.4 升力

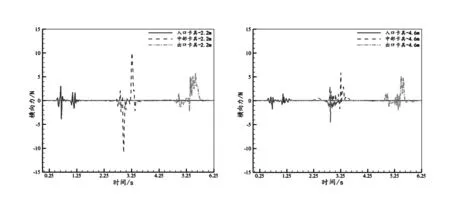
表5给出的是500 km/h的列车通过隧道时卡具的升力变化量。当列车车速从350 km/h提高到500 km/h时，中部卡具升力正负峰值最高，分别为8.1 N和-8.04 N。数值得到工况2不同位置处及不同高度卡具的升力曲线如图12所示。

表5 工况2卡具升力峰值表 N

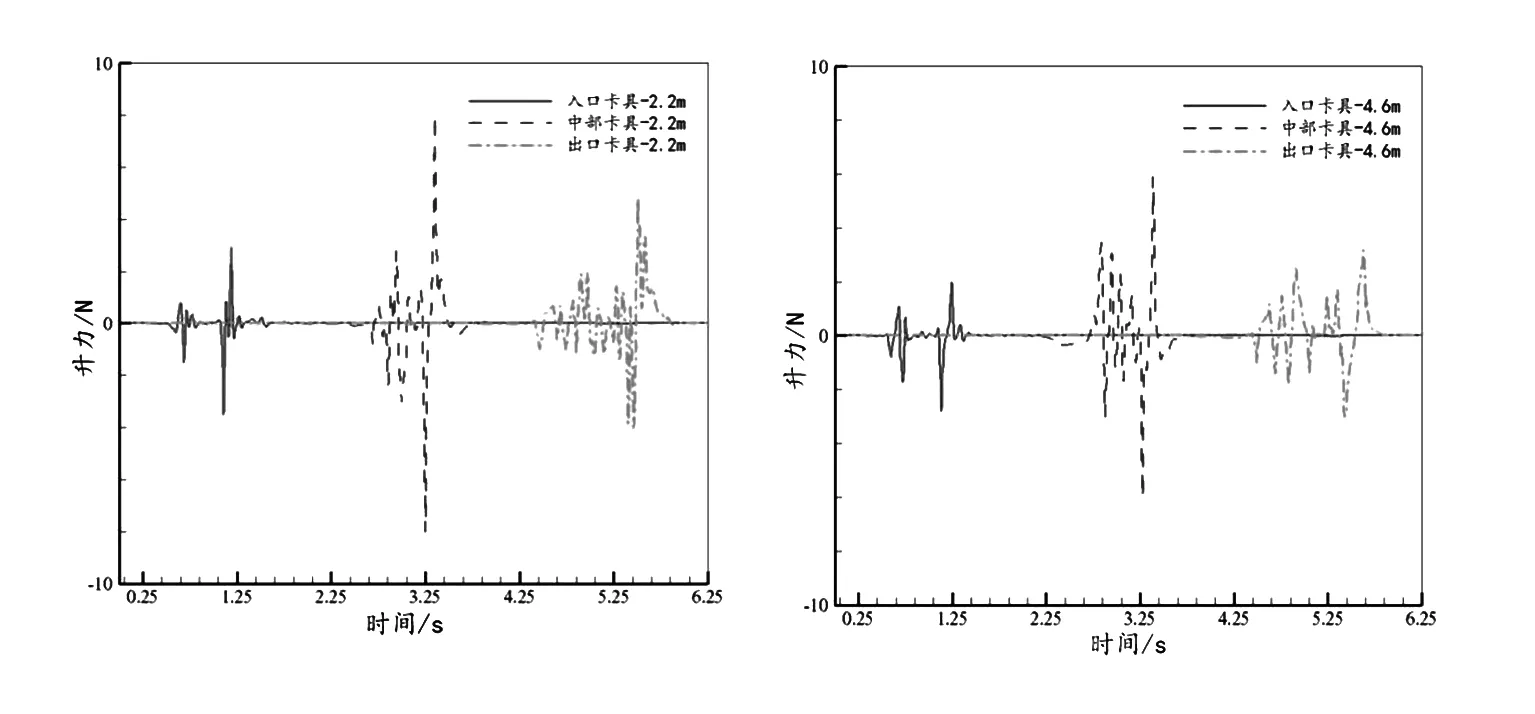
a:高度2.2 m b:高度4.6 m

由图12可知：与横向力相比卡具升力的数值都下降了一个量级，但曲线与横向力曲线相似，都存在两个峰值，说明当列车经过时卡具不断上下振动；随着头车的靠近，卡具升力首先向负波动，有下沉的趋势；当头车鼻尖到达卡具所在位置后，其升力正向波动后迅速下降达到负峰值，即有上浮再下沉的运动趋势；列车经过卡具的过程中，其升力不断正负波动；之后受列车尾流的影响，卡具升力在短时间内由负峰值达到正峰值，说明尾车经过时卡具上下振动比较为剧烈，其中位于隧道中部卡具所受振动与入口与出口两处卡具相比最为剧烈。高度值为2.2 m的3组卡具的升力正负波动普遍大于高度为4.6 m的3组卡具，与横向力分析结果相似，更接近车头鼻尖高度的卡具受力更大。

5.5 纵向力

表6给出的是500 km/h的列车通过隧道时卡具的纵向力变化量。当列车车速从350 km/h提高到500 km/h时，中部卡具纵向力正负峰值最高，分别为6.48 N和-8.63 N。工况2不同位置处卡具的纵向力曲线如图13所示。

表6 工况2卡具纵向力峰值表 N

相比于横向力和升力，卡具的纵向力曲线振幅减弱了许多。相似的，高2.2 m的卡具纵向力大于高4.6 m的卡具，而且位于隧道中部的卡具纵向力值最大；当头车接近卡具时，卡具在纵向上有向前的运动趋势；卡具在尾车经过前后是有先向前接着向后运动的趋势；随着尾车不断远离卡具时，卡具依然处于微弱的前后振动中。但由于卡具在隧道横截面上的投影面积较小，其纵向力数值总体较小。

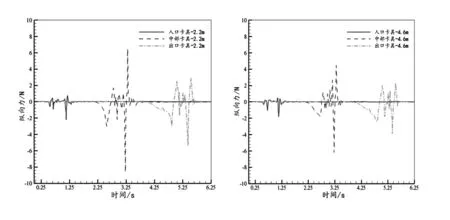
a:高度2.2 m b:高度4.6 m

6 结语

针对列车高速运行时复杂的气动效应，采用动网格技术，建立高速列车绕流流动的控制方程和湍流运输方程，以列车在隧道内运行的工况为例，以保障行车安全的重要设备——隧道用泄漏电缆固定卡具为对象，数值分析了不同运行速度下列车产生的列车风对泄漏电缆固定卡具气动载荷特性，对工况中的6个卡具所受的横向力、升力以及纵向力数值进行纵向对比，得出列车行驶速度为500 km/h时位于隧道中部高度为2.2 m的卡具所受3个方向上的力最大；随着列车速度的提高，漏缆卡具所受压力波到达的越早；更接近车头鼻尖高度的卡具受力更大；研究结果为泄漏电缆固定卡具的刚强度设计提供依据。