黏温效应和不同流动状态下的螺旋槽液膜密封性能
尹中亚,冉海风,俞宴明,张心奕,武余利
(安徽工程大学 机械工程学院,安徽 芜湖 241000)
关键字: 液态金属;螺旋槽;黏温效应;动态特性;湍流
液态金属一般采用镓铟或锡的合金,在常温中为液态。1993年Kezik等[1]探究了镓在不同温度下表现出的润滑性能,得到的结论是摩擦系数比较低,近乎与载荷和速度没有关系;2017年Li等[2]研究发现采用镓基液态金属润滑在极压高载条件下阻止滑动界面焊合。
非接触式机械密封利用动压原理,工作时将静环与动环分离,形成非接触式密封,降低了密封端面间的磨损,引来了国内外许多专家学者的关注,黄建平[3]采用数值模拟的方法,对比了螺旋槽机械密封和普通机械密封,发现在同样参数下普通机械密封各种性能均不如螺旋槽机械密封。张鹏高等[4]分别对内螺旋槽和外螺旋槽在不同液膜厚度和不同转速下的液膜特性作比较,分析了其压力分布、泄露量、液膜开启力、摩擦扭矩等相关参数。Balyakin等[5]提出计算机械密封流体力学特性的数值方法,揭示了间隙尺寸和维度、微型槽等对密封特性的影响规律;2012年Pascovici等[6]考虑了摩擦间隙中的温度,建立了温度场模型,得到了动静环的温度分布情况。温度对润滑介质的存在状态有很大的影响,陈汇龙等[7]以水为润滑介质,考虑了液膜汽化和黏温效应对密封液膜的影响,发现温度增加可以降低流场的动压效应。Lin等[8]分析了高速旋转下的水润滑轴承,发现考虑了空化效应的螺旋槽推力轴承刚度系数大于未考虑空化效应的,并且通过实验进行了验证。
本研究分析了螺旋槽止推轴承密封中液膜压力的形成机制以及结构参数对动态性能的影响。探究了不同流动状态下流场的特性;研究了温度对黏度的影响;研究了结构参数与工况参数对螺旋槽液膜密封性能的影响,确定了各参数的最优取值。
1 计算模型的建立
1.1 基本假设
通过数值模拟工具能够清楚地看到模型内部流体流动的细节以及流动的规律。但由于密封在实际运行中内部流场的复杂性,需要对计算模型进行简化,对密封端面液体润滑膜作出如下假设:
(1)润滑介质为牛顿流体,为不可压缩流体;
(2)由于液膜为微米级,忽略体积力和惯性力作用;如重力、磁力;
(3)润滑介质与密封表面吸附牢固,无相对滑移;
(4)密封为刚性端面。忽略密封环变形对流体流动的影响。
1.2 几何模型
图1示出了螺旋槽端面密封的工作环境,在高速旋转下,端面加工不同形状的凹槽将产生流体动压效应,不同的凹槽产生的油膜力大小也不同。常见的螺旋槽结构有阿基米德螺旋线、对数螺旋线。本文研究的螺旋槽线型采用对数螺旋线,极坐标下公式为:

图1 螺旋槽结构图
r=rg×eθtanα
(1)
式中,rg为螺旋槽的内半径,α为螺旋角,θ为转角。
选择表1中几何参数作为模型参数,若下文不做说明均以表1参数为准。由于螺旋槽推力轴承表面槽台数目较多,且其具有周期性分布的特点,为了便于进行研究,取1对槽台油膜模型为计算对象。用SolidWorks进行三维建模,模型如图2所示,由于非接触式机械密封中液膜X、Y轴方向为毫米级,厚度方向为微米级,为了直观展现,在Z轴方向也就是厚度方向放大 100倍显示。

表1 螺旋槽端面密封几何模型参数

图2 计算区域及边界条件设置 图3 剖分方案
1.3 控制方程的建立
密封端面是对称的,则机构端面间在圆柱坐标系下的流体流动雷诺方程[9]为 :
(2)
引入下列公式
(3)
改写公式(2)改为
(4)

求解该问题所需的边界条件为,在密封环的内径ri,压力等于被密封的介质压力pi;在密封环的外径r0处,压力等于被密封的介质压力p0即
p|r=r0=p0
p|r=ri=pi
(5)
周期性边界条件:
p(θ+2π/Ng)=p(θ)
本文所用的的黏温曲线方程[10]为:
lnv=-0.006050T-0.489469
(6)
轴承承载力计算公式:
(7)
液体泄漏量
液体通过密封端面的泄漏量可以用液体流过密封坝的体积流量[11]表示,其计算式为:
(8)
1.4 网格划分及边界条件设定
由于端面螺旋槽呈周期性均匀分布,建立了液膜的单周期模型。考虑到密封间隙流体膜的模型较特殊,Z轴方向为微米级,给网格划分带来许多不便,为了得到网格质量更高的网格单元,用了分区域划法。模型分块方案如图3所示,在XY平面里将槽区与坝区分隔开,方便后续的扫描划分;密封端面与源面选择互为平行面的关系,四边形为主,单元格及网格尺寸,节点的控制设定为统一的全局控制。

图4 网格效果图
边界条件设置:将周期分割面设置为旋转周期边界条件,密封环外径处设置为压力入口边界,值为0.5 MPa,密封环内径处设置为压力出口边界,大小为0.1 MPa,转子止推面为旋转固壁面,其它部分的壁面设置为绝热、无滑移边界。

表2 网格数量与压力峰值
当网格数量从28 185增加到66 388时,流场的压力峰值增幅为9.6%;当网格数量从66 388增加到233 162时,流场的压力峰值增幅为1.6%;当网格数量从233 162增加到445 668时,流场的压力峰值增幅为0.6%。因此,可以设置尺寸为0.1 mm的网格,确定网格单元数量为233 162。
2 结果与分析
2.1 模型验证
利用本文的计算方法对李宁等[9]研究中的螺旋槽机械密封(模型参数见表3。)进行验证,润滑介质采用水。

表3 模型参数
验证结果如图5所示,结果与李宁等研究中关于动环压力分布规律一致;并且提取了径向不同半径处的压力值,将验证的结果与文献数据分析,得到了沿半径的压力分布曲线图6。说明在槽根处存在高压区,端面开槽可以增大液膜的压力,实现动环与静环的非接触密封。两种模型计算趋势一致并且数据误差不超过12%,因此本文所建的模型和分析方法是可靠的。

图5 不同半径下的压力值

图6 沿半径压力分布曲线图
2.2 端面液膜的压力分布
采用表1的参数,由于流体膜厚只有几个微米,在建模时将其在膜厚方向上放大100倍,利用Fluent2020R2软件的缩放功能,解决这种尺寸跨度过大的问题。选择Simplec 压力速度耦合算法,其它控制参数保持默认。如图7所示,采用的物理模型是湍流,选择标准壁面函数,开启能量方程,考虑了内摩擦;得到了螺旋槽端面液膜的总压力和静压力云图。

图7 螺旋槽端面液膜的总压力和静压力云图
从图7可以看出,总压和静压分布规律基本相同,在径向方向液膜压力沿槽逐渐增加,在槽台交界处最大,然后沿台逐渐下降。在密封环的内外径出现了明显的低压,这是由于液态金属在螺旋槽内受到堰台的阻碍,导致液态金属聚集在槽根处,出现压力峰值,是液膜密封的承载区域。
2.3 层流与湍流的比较
层流与湍流的本质区别是:层流没有径向脉动,而湍流有径向脉动。湍流是自然界中常见的一种流动状态。本文比较分析了层流和湍流状态下液态金属在螺旋槽中的流场特性。将2.2中的模型换成层流,得到图8所示的液膜的总压力和静压力云图。从图8中可知层流和湍流两种流场都能产生泵压效应,压力分布规律基本相同,都是在槽根处出现压力峰值。从压力峰值可以发现,湍流状态下具有明显的泵压效应,止推轴承承压能力将更好。从图9中可以看出在不同转速下湍流的压力峰值均高于层流,同时轴向承载力也是湍流高于层流,刚度也是湍流优于层流状态。因而下文均用湍流模型进行研究。
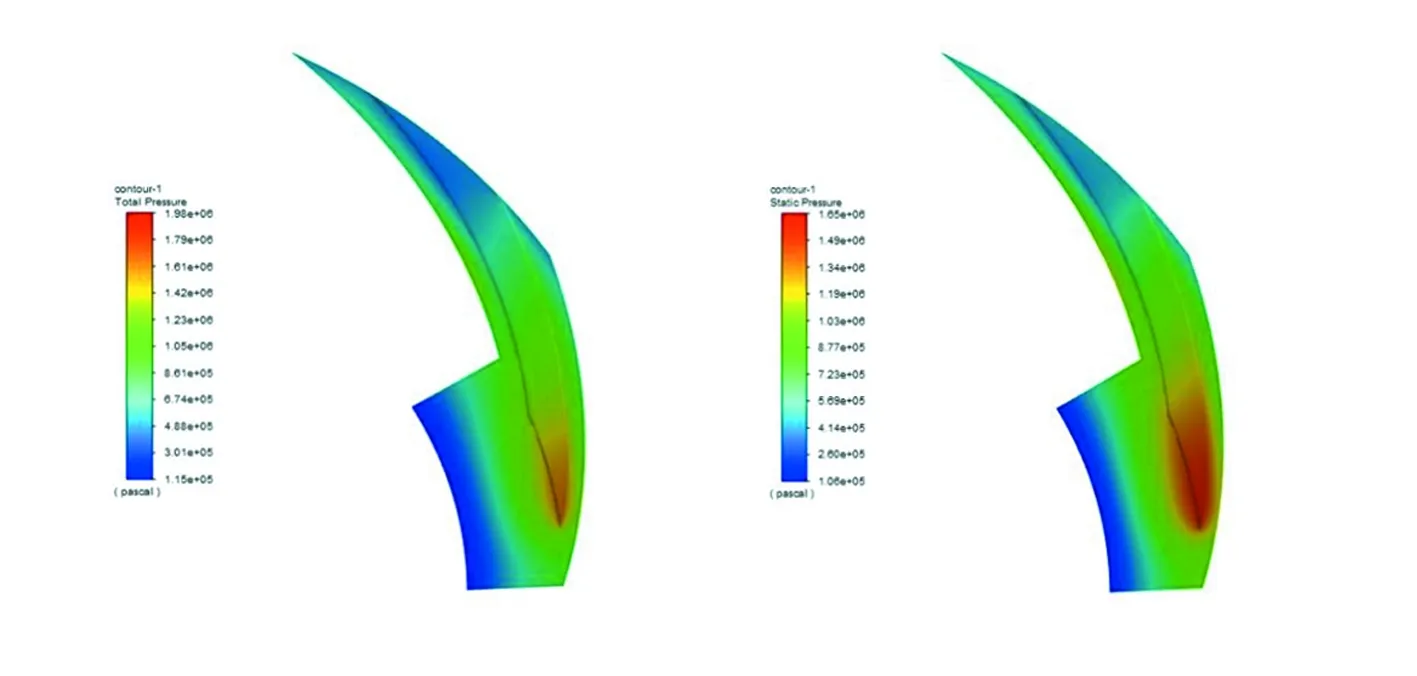
图8 液膜的总压力和静压力云图

图9 不同转速下湍流和层流的压力峰值与承载力
2.4 黏温对螺旋槽液膜的影响
温度升高,液体的黏度减小。在仿真计算中,如果考虑复杂工况下的模型,往往会出现计算结果不收敛的情况,如果不考虑这些因素,又将导致实验数据与计算结果有较大差别。因此,探究黏温效应下流场的特性十分有必要。将液态金属的黏温方程用UDF(user defined function)形式加载到Fluent2020R2进行计算。黏温方程如公式(6)所示,从图10可以发现,温度越高,液态金属的黏度越低,流场在高速旋转下黏性生热,产生的热对流场中的黏度起作用。从图11曲线可以得出黏温作用下螺旋槽动压效应降低,承载力也同步下降。
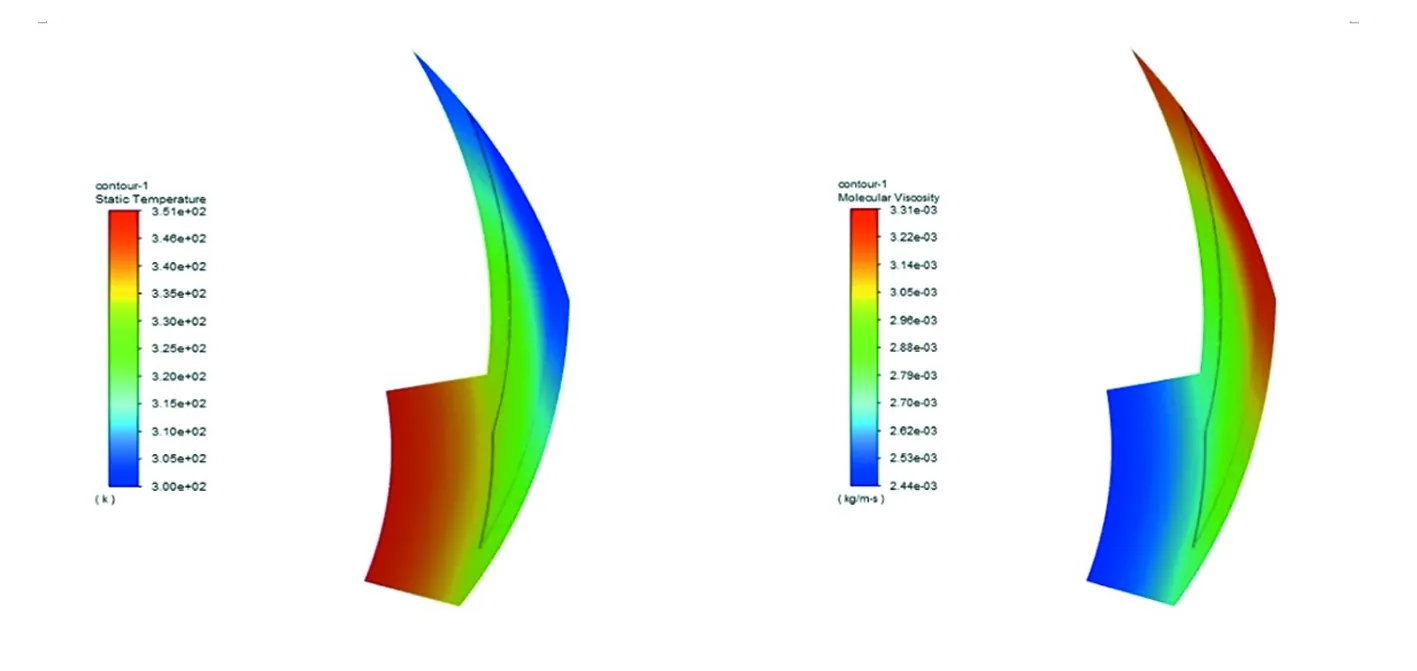
图10 温度分布与黏度分布云图

图11 不同转速定黏度与黏温效应下的压力峰值和承载力变化
从图11表现出当考虑到黏温效应时,压力峰值和承载力都有大幅度的下降,可以得到润滑液的温度对液膜的密封性能有较大的影响,要给予考虑。
2.5 结构参数对螺旋槽液膜的影响
螺旋角α是螺旋槽设计的一个重要结构参数,随着液体进入螺旋槽后将沿槽线不断升压,产生动压效应。本文研究了螺旋角从15°~19°的密封性能,由图12发现,随着α的增大,螺旋槽的承载力整体呈现上升后又迅速下降,出现这个现象的原因是不同的螺旋角产生的动压能力不同。当使用极限的思想时,螺旋角为0°或者90°,动压阶梯效应会迅速降低,承载力几乎完全消失。因此螺旋槽止推轴承的螺旋角可以取18°。图12可以看出螺旋槽在改变螺旋角和增加转速对泄露量的影响。转速增大,泄露量也会跟着增大,当螺旋角从15°增大到19°时,泄露量也是不断增加的,在15°~18°增长较为缓慢。螺旋角的增大使得内径侧槽根处的低压区域有所缩减,削弱了低压回吸能力,导致泄露量增大。
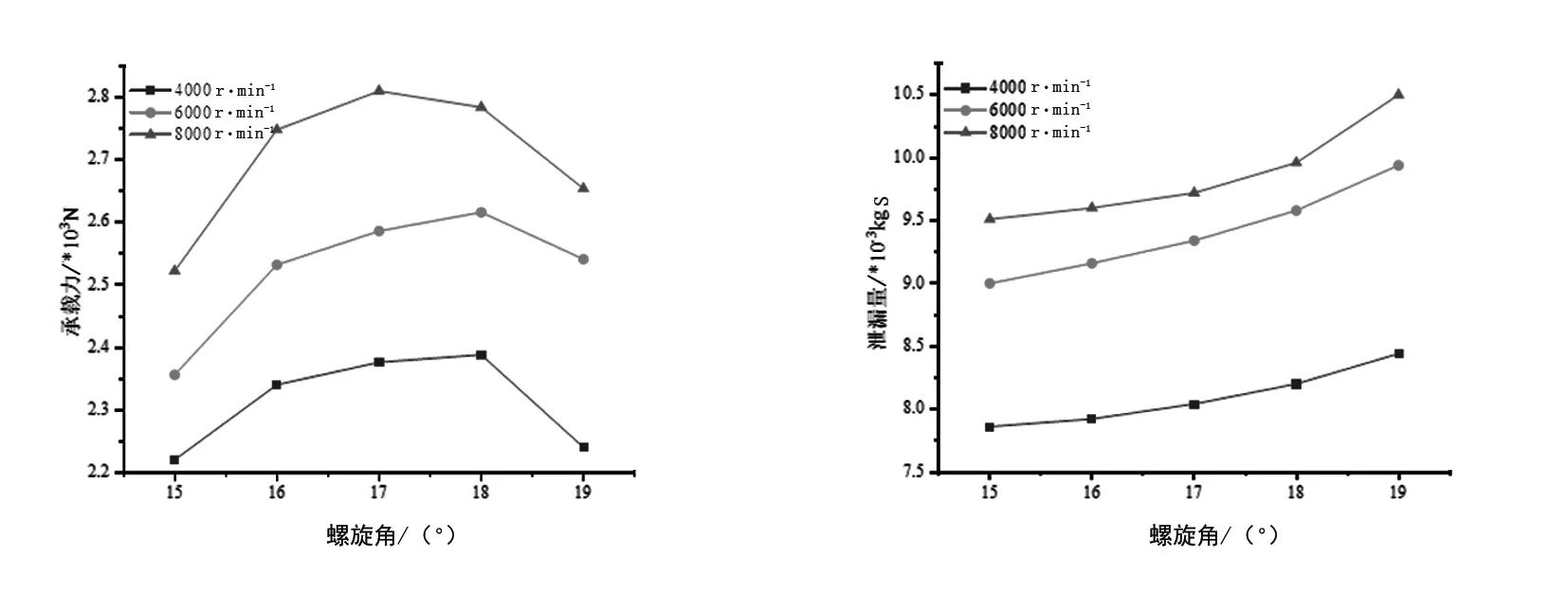
图12 不同螺旋角和不同转速对应的承载力与泄漏量
从图13可看出,螺旋槽的承载力在不同转速下,随着槽数的增加而增大,当槽数超过18个之后承载力趋于稳定,泄露量随着槽数增多而增大。这是因为槽数低时,轴承的阶梯动压效应不足;当槽数增加时,轴承的动压效应明显增强,随之承载力得到提高;当槽数增加到一定时,动压效应却不会无限增大。槽数的不断增多使得靠近内径侧的低压区域有所增加,这样会让螺旋槽内的回流能力加强,同样增多的螺旋槽数又会让整体的泵送能力加强,所以能很好地降低泄露量;同样转速下槽数越多对泄露量的控制越好。不难发现增加槽数和提高转速有利于控制螺旋槽的泄露量。但是槽数的不断增加会提高加工的难度和增大成本,因此需要合理控制槽数。

图13 螺旋槽不同转速和槽数对应的承载力与泄漏量
3 结论
本研究首先比较分析了层流和湍流状态下液态金属在螺旋槽中的流场特性,得到了总压力和静压力云图,从图中看出层流和湍流都能产出泵压效应,但从槽根处的压力峰值可以看出,湍流产生明显的泵压效应。随后,分析了黏温特性对螺旋槽液膜的影响,通过仿真计算得出温度越高,液态金属黏度越低,符合实际理论。且通过数据比较得出黏温效应对螺旋槽承载力和压力峰值影响较大,所以现实中不能忽略其对密封性能的影响。最后,分析了螺旋槽在不同转速、不同螺旋角、不同槽数时承载力和泄露量变化。结果表明,在提高转速增加槽数及增大螺旋角,螺旋槽的承载力和泄漏量都表现得更佳。不同参数的改变都会不同程度影响着机械密封的综合性能,因此在设计取值时要综合权衡工作环境、指标要求等因素。

