基于补偿GNSS滞后的实时外推时间配准方法
吴 涛,朱建良,周 维
(南京理工大学 自动化学院,南京 210094)
随着科技的不断发展,当代生活对导航装置的定位精度提出了更高的要求。目前在导航定位领域,GNSS/INS组合导航系统是不可或缺的一环。由于GNSS信号存在较大解算和传输时滞,该滞后会产生较大的观测误差,从而导致融合效果不理想,降低了导航精度。通过时间配准,可以较好解决异步异质传感器带来的时间误差问题。
导航系统中由于存在各个传感采用不同的时间基准、采样频率和开机时刻不一致以及存在通信时延等问题,所以在数据融合前应先对不同的导航数据进行时间配准,将其统一在相同的时间坐标下,确保GNSS,INS输出的导航数据都是基于统一的有效时间。如果导航数据没有经过时间配准而直接进行融合,滤波过程中会错误估计系统状态,导致融合效果不理想,降低导航精度。
在GNSS/INS组合导航系统中,由于卫星信号数据量较大,故其解算和传输将产生较大时滞[1]。目前,针对GNSS/INS组合导航系统,许多学者提出了不同的时间配准方案。杨涛等[2]通过检测GNSS的1PPS脉冲对A/D转换器进行同步采样,实现了MIMU和GNSS数据在更新时刻的同步采集,但是此方案忽略了因GNSS数据量较大、传输速率有限造成的传输时滞,这将造成较大的导航误差。游文虎等[3]通过中断计时的方式获取SINS更新时刻与GNSS的秒脉冲到来时刻的时间差,选取GNSS数据传输完成时刻作为配准时刻,并利用在此时刻采集到的IMU数据外推GNSS数据至配准时刻,在配准时刻IMU数据也是未知的,还需要对IMU数据进行外推,会产生较大的计算时滞,增加处理器负担。李倩等[4]选取秒脉冲时刻为配准时刻,并采用数据缓存法,当卫星信号传输完毕后,在缓存区找出对应的惯导解算数据,但该方法实时性较差。
在GNSS/INS组合导航系统中,考虑到(1)两种传感器的采样频率可能不是整数倍;(2)GNSS信号存在解算时延;(3)时间配准的实时性等情况,提出一种基于补偿GNSS解算滞后的实时外推时间配准方法,使不同的导航信息都处于相同的时间坐标下,旨在提高GNSS/INS组合导航的定位精度。
1 时间误差的来源与影响
1.1 误差来源
GNSS/INS组合导航系统实质上是一个导航信息的融合优化系统,GNSS与IMU相互辅助,提供误差观测量进行数据融合滤波,以此提高导航精度[5]。数据融合首先要面临就是各导航数据时间不同步问题,其产生的原因主要有以下几点[6]:
(1)GNSS和IMU的时间基准不一致;
(2)GNSS和IMU的采样频率和采样起始时刻不一致;
(3)GNSS和IMU在各自解算输出时,存在计算及通信时延;
(4)IMU存在时钟漂移,导致GNSS与IMU存在时标差。
在GNSS/INS组合导航系统中,GNSS的导航信息是以1PPS信号的上升沿时刻(即整秒时刻)作为时间戳,目前GNSS/INS组合导航系统大多以GNSS信息到达时刻作为融合时刻。实际上,由于解算和通信的时延,GNSS和IMU数据的采集时刻与解算输出的时刻存在时间不同步现象,其中卫星信号到达GNSS接收机后,GNSS处理模块需要先进行一系列的解算,再将结果传输至融合单元。其中解算时长大约为10~20 ms,当传输波特率为115 200时,传输时间约为10 ms,故GNSS具有较大的解算输出滞后,通过示波器实际量测,结果如图1所示:

图1 GNSS信号传输完毕时刻
由图1可知,GNSS的导航信息传输完成时刻与1PPS信号大约滞后47 ms。相对于GNSS,IMU的滞后约为1 ms,故IMU的滞后可忽略不计,下面都只考虑GNSS信号的滞后问题。
以上情况会导致滤波过程中错误估计系统状态,导致融合效果不理想,降低导航精度。
1.2 误差影响
为了分析上述时间误差会造成的影响,分别讨论时间误差与速度、位置之间的关系。
1.2.1时间误差对速度估计的影响
针对GNSS/SINS导航系统,设时间误差为△t,选取速度误差为观测量,建立两维速度观测方程[7]:
(1)
其中vEINS,vNINS分别是惯导解算出的载体东向速度和北向速度,vEGPS,vNGPS分别是卫星测得的载体东向速度和北向速度,△t为卫星与惯导之间的时间误差,vE(t),vN(t)为载体在配准时刻的速度真值,δvE,δvN为惯导解算的速度误差,vE(t-△t),vN(t-△t)是GNSS测得的载体运动速度真值,v'E,v'N是GNSS测量的速度误差。
由式(1)可知,速度误差与时间误差△t有以下关系:


1.2.2时间误差对位置估计的影响
在GNSS/SINS组合导航中,GNSS与SINS的时间误差为△t,选取位置为观测量[8]:
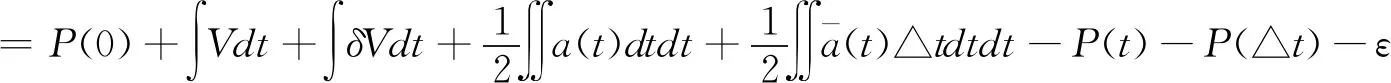
(2)

目前卫星导航系统常采用实时差分定位技术(RTK),该技术可实现厘米级定位。若行车速度为80 km/h,GNSS信号的时滞将会导致约0.8 m的导航误差。
综上所述,GNSS/SINS导航系统中时间误差△t会对导航状态估计产生影响,从而使导航精度下降,所以通过时间配准方法来消除时间误差。
2 时间配准
时间配准就是将系统中的各量测信息都统一到相同的时间坐标系中,为之后的数据融合做准备[9]。在上述分析的误差来源中,针对时间基准和时钟漂移的情况,可将GNSS中的1PPS信号作为统一的时间基准[10],由1PPS信号分频得到高频的脉冲信号,以此触发IMU进行数据采集输出。针对GNSS/INS采样频率不一致和存在计算时延的情况,可采用实时外推时间配准法,实时估计拟合出配准时刻的GNSS和IMU观测值[11]。
2.1 时间基准
在GNSS/INS组合导航系统中,GNSS的采样频率相对于IMU较低,一般GNSS的采样频率为1~10 Hz,而IMU的采样频率一般可设置为50~1000 Hz。其中IMU存在时钟漂移,即使GNSS和IMU同时启动,两者之间依旧会产生时标差[12]。
针对时间基准不一致和IMU存在时钟漂移的情况,可将GNSS中的1PPS信号作为统一的时间基准,由1PPS信号触发1~100 Hz的可调脉冲(见图2),IMU以高精度的可调脉冲信号作为参考时标进行数据采集,当1PPS信号再次到来时,对之前触发的可调脉冲进行校正,这样就可以消除时间基准和时钟漂移带来的累计误差[13]。
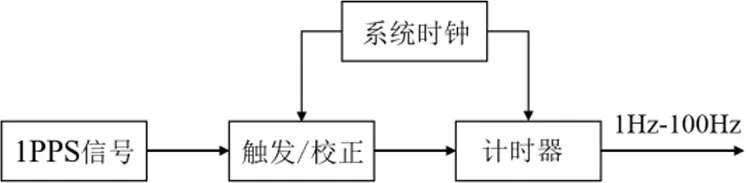
图2 1PPS触发可调脉冲
若设定IMU的采样频率为100 Hz,即1PPS信号需触发100 Hz的脉冲序列,通过实验多次测量,试验结果见表1。

表1 PPS 与其触发产生的 100 Hz 时钟的同步误差 ns
由表1可得,1PPS与其触发脉冲时钟沿误差最大为 965.0 ns,如图3所示,最小为32.9 ns,满足导航系统的精度要求。将1PPS信号分频作为IMU的参考时标,可以较大程度上消除时间基准和时钟漂移带来的累计误差。

图3 1PPS与其触发脉冲最大时钟沿误差
2.2 时间配准方法
消除时间基准和时钟漂移的误差影响后,针对GNSS信号的时间滞后问题,首先应选择一个合适的配准时刻,再利用实时外推时间配准算法将两种导航信息统一至相同的时间坐标系下。
2.2.1配准时刻的选择
时间配准首先需要选择合适的配准时刻,使各传感器在同一时刻进行量测信息的时间对齐。
GNSS信号由于存在上述的滞后问题,如图4所示,从而导致IMU与GNSS之间存在时间差dti(i=1,2,3,…)。

图4 GNSS时间戳与导航信息时间不匹配
目前配准时刻的选取主要有两种方案:
(1)选取秒脉冲时刻为配准时刻:当卫星信号传输完毕后,在数据缓存区中找出对应时刻的IMU数据,两者进行数据融合,但此时载体已经运动了一个滞后周期,故此方案实时性较差。
(2)选取卫星信号传输完毕时刻为配准时刻:利用保持器将卫星信号由秒脉冲处合理外推至配准时刻,但IMU在配准时刻也可能没有更新,此时还需要对IMU进行外推,该方案计算量较大,程序执行也会产生较大时滞,故实时性、可行性较差。
针对该情况且考虑到实时性,选取GNSS导航信息传输完成后的第一个IMU数据更新时刻为配准时刻。该方案仅需外推GNSS信息,且弥补了方案(1)中实时性较差的缺陷。利用实时外推时间配准方法,可以得到在配准时刻的GNSS/INS量测值,为之后的数据融合做准备。
2.2.2实时外推时间配准方法
针对GNSS/INS组合导航系统,时间配准就是在配准时刻得到GNSS和IMU对应的量测值。针对GNSS存在滞后的情况,采用实时外推时间配准方法进行时间同步,具体方法如下:
(1)获取IMU数据:当GNSS的1PPS信号来临时(记为t1),由1PPS信号触发单片机的外部中断,使IMU进行惯导数据采集并开始进行GNSS导航数据解算,采用1PPS信号进行触发还可以校正IMU与GNSS的时标偏差,使IMU的整秒时刻与GNSS的1PPS秒脉冲时刻对齐;当导航数据传输完成时,获取下一个时刻(记为t2)的IMU惯导数据,其中的时间差为△t=t2-t1;
(2)计算△SINS:GNSS的滞后时长虽然有几十毫秒,但IMU在短时间内精度较高,所以可根据(1)中获取的2次惯导解算数据和两者之间的时间差来计算GNSS在滞后时间内的状态变化量;
△SINS=XSINS(TPPS+△t)-XSINS(TPPS)
(3)
其中:△SINS是在时间差△t内SINS增量,XSINS(TPPS+△t)是SINS在配准时刻的导航信息,XSINS(TPPS)是SINS在秒脉冲到达时刻(即1PPS时刻)的导航信息。
(3)得到配准时刻的量测数据:其中配准时刻的惯导数据已知,1PPS处的GNSS数据加上(2)的△SINS,即可得到配准时刻的GNSS数据。
XGPS(TPPS+△t)=XGPS(TPPS)+△SINS
(4)
其中:XGPS(TPPS)分别是GNSS在配准时刻的导航信息,XGPS(TPPS)分别是GNSS在秒脉冲到达时刻(即1PPS时刻)的导航信息。
(4)数据融合:通过步骤(1)~(3),即可得到配准时刻GNSS/INS的量测数据,两者是对应同一时刻的载体运动状态,故可以在配准时刻进行数据融合。
综上所述,该方法在配准时刻,仅需对惯导解算的位置、速度信息进行简单处理,便可使两种导航数据在配准时刻对齐,其中程序运行时耗远远低于GNSS几十毫秒的滞后,故该方案实时性得以较好的保证。
3 试验验证
为验证上述时间配准方法在GNSS/INS组合导航系统中实际应用时的性能,设计车载实验方案,分别记录时间配准前后的实验数据,分析所提时间配准方案的可行性。
3.1 试验方案
利用定制铝板搭建车载试验平台,包括捷联惯组、北斗高精度定位系统(包括基准站和移动站)、两个同型号天线、24 V电源、融合解算单元(见图5)。整个跑车试验,将该试验平台固定于车顶。试验前先对惯组进行10 min预热并对RTK进行配置。跑车的初始位置是(32。,118。,46m),初始速度为(0,0,0)m/s,前进方向与北向夹角90°,其中SINS的基本参数为:陀螺漂移约3°/h,加速度计零偏约为20 μg,其中IMU的输出频率为100 Hz。

图5 试验平台结构
3.2 结果与分析
3.2.1配准结果
基于实际跑车数据进行数据插值,将配准时刻实时外推得到的GNSS数据和插值拟合的GNSS数据进行离线分析,时间区间为[60 s,100 s],东向速度配准结果如图6所示。

图6 速度配准结果
由图6可以看出,基于实时外推的时间配准方法能较好地反映跟踪真实的GNSS数据,均方根误差为0.127,具有良好的可行性和稳定性,为之后的数据融合做准备。
3.2.2融合结果
采用卡尔曼(Kalman)滤波算法进行数据融合,状态量为姿态角误差[φxφyφz]T、速度误差[δVxδVyδVz]T、位置误差[δLδλδh]T、陀螺仪零偏误差[εxεyεz]T,加速度计零偏误差[xyz]T,共计15维,具体可表示为:X=[φxφyφzδVxδVyδVzδLδλδhεx
εyεzxyz]T,选取观测量为位置与速度误差,建立观测方程。
由图7和图8可知,未经过时间配准处理得到的二维位置与真实轨迹存在较大的偏差,而经过时间配准处理后得到的位置信息与真实轨迹吻合度有了较大的提高。
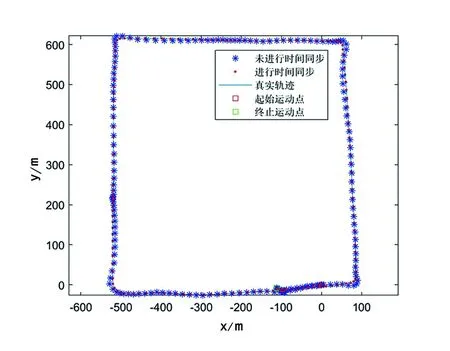
图7 运动轨迹
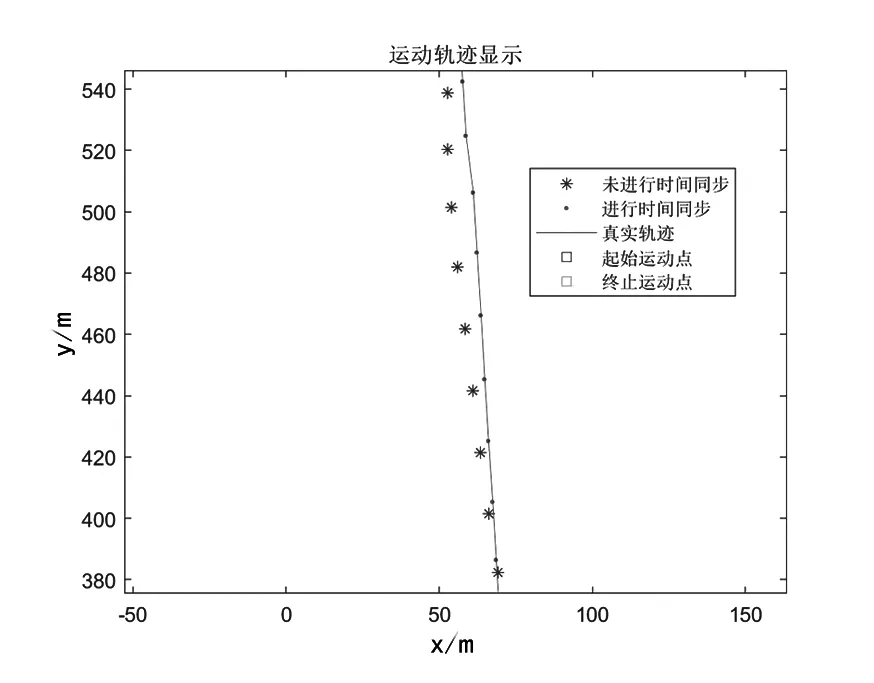
图8 运动轨迹局部
为了直观地比较时间配准前后的导航效果,列出了时间配准前后的导航参数误差(见表2),误差由均方根误差(RMSE)表示。结果表明所提出的时间配准方法有较好的可行性,提高了导航定位精度,提高了约40%。
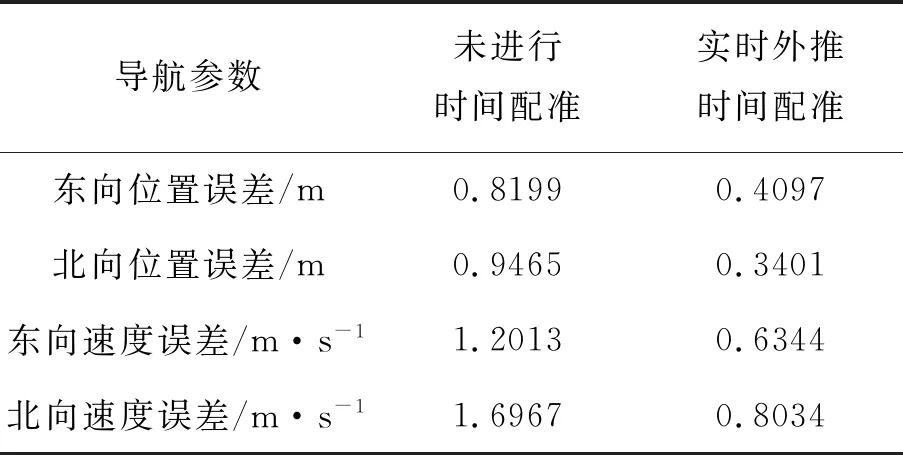
表2 导航参数对比
4 结论
针对GNSS/INS组合导航中时间不同步问题,本文利用1PPS信号作为时间基准源,将其分频作为IMU的参考时标,消除了IMU时钟漂移带来的累计误差,此外考虑到GNSS信号存在滞后问题,采用实时外推时间配准方法,将GNSS/INS统一到相同的时间坐标下,实现了GNSS/INS数据的实时同步输出。经试验验证,该方法软硬件实现较为简单,能有效提高定位精度,但目前仅为车载验证,由于道路速度限制,属于低速运动,缺乏普遍性,之后会将该时间配准方法应用到不同的复杂环境中,以此验证其在更广泛速度、地理范围的可行性。

