采用偏序集层次聚类的多准则决策方法

朱旭光，沈玉志

（1.辽宁工程技术大学 创新实践学院，辽宁 阜新 123000；2.辽宁工程技术大学 教务处，辽宁 阜新 123000）

0 引言

决策通常指从多种可能中做出选择和决定，多准则决策是指在多维度空间中，将可能具有冲突、不可共度的方案集中做出选择的过程. 传统方法过于依赖指标权重数值，且不能展示解集的层次结构，当权重未知时传统方法显得力不从心，基于此，采用偏序集理论，融入偏好信息，将聚类分析应用于多准则决策，能较好的解决以上问题.

传统决策方法往往关注最优解或满意解，但有时决策结果并非单解，所以有些学者尝试将多准则决策方法与聚类方法相结合，进而突出决策领域的优势，如文献[1].文献[2]提出一个决策模型，与聚类算法相结合，利用学习平台上可用的不同数据集，根据学习者的行为和专业知识对学习者进行分类.提出了一种多智能体方法，该方法使用智能代理来表示参与者，实现多准则决策模型进而优化学习过程.类似研究还有文献[3]～文献[7]等，分别针对不同应用，优化了决策模型，利用不同决策方法或评价方法，对目标样本进行考察.

聚类分析的决策方法没能解决解集分层问题，决策过程只注重方法和求解原则的选择，而忽略了解的性质.决策过程的解往往不是单独的，而是一个集合，这个集合可能是非完全序的，也可能是偏序的.已有研究没有将层次聚类分析应用于多准则决策领域，没有对决策结果进行分层[8-18].基于此，尝试采用偏序集理论，融入偏好信息，利用层次聚类分析优化传统多准则决策方法，并验证方法的有效性.

1 基于偏序集层次聚类决策方法

1.1 层次聚类

层次聚类分析法中的层次关系，并不是类之间的上下级层次，而是在聚类过程中的范围层次，即一种演绎-归纳层次，并没有体现类与类之间的等级层次，即上下级层次关系.层次聚类的层，并没有绝对的邻接关系，可能从这几个样本开始聚类，得到某种层次关系，类似地球土层.从其他样本开始聚类，又得到其他层次关系，总之，层次关系不固定，体现不出类别间的上下级关系以及相邻层关系.

已有聚类算法并不适用如何解释密度分散情况.此n1个样本密度为d1，n2个样本密度为d2，依次类推.d1，d2，……无法比较谁更密.利用偏序集理论进行层次聚类可解决，同类基本都在相邻层次，有的层宽，有的层窄，分散点、离群点通常位于最顶层或最底层.

20世纪50年代，学者们已利用层次结构进行数据描述，典型的就是树状结构.对树状图中包含的信息的解释通常是以下类型：集合包含关系、对象集合的分区和有效集群划分.在这种情况下，树状图提供了一个精确的潜在展示模型.

通过在树状图上进行查找，相当于在拓扑空间以最佳逼近的方式找到聚类簇.这种方法是一种拓扑方法（基于集合及其属性），是使用更广泛的优化或统计方法.总之，一个树状图聚集了许多接近性或同分类关系的数据体，可以通过树状图提供相应的聚类结果.而利用偏序矩阵计算出哈斯矩阵，其对应的哈斯图，与这种层次结构是非常契合的.

1.2 基于偏序集层次聚类

传统层次聚类是从任意样本开始，计算任意样本距离，将距离近的算作一类，再计算类间距离.从计算任意两样本距离再到类间距离测算，耗费大量运算时间.基于此，利用偏序集理论改写层次聚类方法.

定义1设R是集合A上的一个二元关系，若R满足

（1）自反性：对任意xA∈ ，有xRx.

（2）反对称性：对任意,xyA∈ ，若xRy且yRx，则xy= .

（3）传递性：对任意 ,,xyzA∈ ，若xRy且yRz，则xRz.

则称R为A上的偏序关系[19].

传统二阶聚类[20]首先构建聚类特征树.把某样本作为树的根节点，依据距离计算公式，计算样本间的亲疏程度，可以标定一个临界值，把其他样本放到最近的样本中；如果某样本没落在临界值里，即没有找到与它足够近的节点，就让它成为一个新的节点.而采用偏序集方法生成的哈斯图，可以通过相邻层次查看亲疏程度，即在矩阵里完全体现，所以更能提高聚类效率.

每一个样本有多个指标，这些指标重要性可能相等，也可能有主次之分.如果各指标同等重要，即所有指标都是等权重的，则采用传统偏序集计算方法.若这些指标是非等权重的，那么，得到指标的权重顺序即可，采用岳立柱[21]等人提出的偏序集计算方法进行比较运算.算法步骤如下.

步骤1对于有多个指标（准则）的待分类数据，取某一重要指标或某一变化范围大的指标，将该指标下的值进行排序，根据具体问题也可不排序.

步骤2依据数据规模进行划分，可等分成n份或随机分割.

步骤3根据步骤2所得出的指标数值范围，取各个划分下的所有样本.

步骤4从步骤3中任选1个样本，同时，在其所在划分中将其删除.

步骤5计算步骤4中那例样本与各个划分中所有样本对应指标之差，并求出平方，也可开方取正值，对差值进行多准则聚类分层分析，共计n个哈斯图.根据各个哈斯图高度数值，即层次数值，算出每层平均节点个数Ti（i=1，2，…，n）.

步骤6计算步骤5中每个哈斯图超过本图Ti的层次个数Mi（i=1，2，…，n）.

步骤7计算步骤6中层次个数的总数即

步骤8得出种类数P=SUM/n，如此确定类别数.

步骤9取最高层次所有样本，如果所有哈斯图最高层都只有一个节点，可以将其定为噪声，否则，取出所有最高层对应的样本，作为一类.

步骤10循环步骤6，将取出了高层的各划分剩余样本与步骤4中样本各个指标做差，并求出平方，也可开方取正值，再进行聚类分层，即再求出n个哈斯图，仍然取最高层所有样本作为一类，并归并入步骤6所得到的类中，如果某划分所求出来的哈斯图最高层只有一个节点，说明此划分对应此类已经聚类完毕，下次不用再计算.

步骤11循环步骤6、步骤7，直到所有划分求出哈斯图后，得出最高层只有一个节点时，此类聚类完毕.

步骤12从剩余各划分中，任意选出一个样本，同时，在其所在划分中，将此样本删除，重复步骤5～步骤8，直至聚类结束.

步骤9中，如果多数划分中最高层只有几个节点，根据BIC准则，可以认定此判别样本为噪声，可以舍弃.否则，针对各划分的数据比例，将高层节点作为一类.再从第二层中任取一个节点，进行本划分层次聚类，如步骤5.判断节点是否基本为其同层或以下顺序层，如果基本符合，说明聚类正确，否则，重新选取样本进行聚类.

定义2设偏序集S为偏序关系R上的一个子集，如果都有最小上界和最大下界，则称S关于偏序关系R为一个格[22].

一个格是指其任意非空有限子集都有一个上确界和一个下确界的偏序集合.一个形式背景上概念格就是一个偏序集簇[23].格论是抽象代数的分支，研究格的性质有助于研究偏序集元素之间的分类和聚类.

根据格的理论，可以定义一个上确界和下确界，之后，根据此界限，确定聚类到第几层，每个划分都根据此上确界进行最高层提取，超过了就不再提取，认为聚类完毕，进行下一轮聚类，直到所确定的种类全部聚类完毕.其中，上确界及下确界的确定可以依据数据规模，也可根据专家经验，也可根据轮廓线理论找到，虽然哪种方式都存在一定主观性，但对于融合了人的信息即偏好序的数据恰恰是很适用的.

定义3令Pi为每一轮迭代随机抽取的样本，经赋权指标加权比较后，得到各层的子集.最高层各节点为U1，第二层各节点为U2，第三层及以后以此类推，可知 ∩Ui=∅.

定义4在一个总体数量为N的样本集中，将N合理划分成n个不相交子集，每个子集生成一个哈斯图，根据各个哈斯图高度数值，即层次数值，算出每层平均节点个数Ti（i=1，2，…，n）.计算出每个哈斯图超过本图Ti的层次个数Mi（i=1，2，…，n），求出层次个数的总数SUM，则聚类簇数为P=SUM/n.

定义5在一个总体为n的样本集中，若各样本到某点距离相等，则称该点为类别中心点，即质心点，简称为质心[9].

定理1由定义5有聚类簇数为P=SUM/n，当P/n⇒ 1时为最佳分类簇数.

证明P/n=(SUM/n) /n=SUM/n2，若P/n⇒1，则有SUM/n2⇒1，则，n≈SUM

（1）当n=1时，若SUM≤1，则说明所有样本都是一类，此划分已是最佳划分，得证.若SUM＞1，因为每个类别中都是相对质心向外发散，肯定会有最密的位置，根据哈斯图原理，若有超过每层平均数的层，则该层就是一类质心附近的点，所以，则最佳分类就是SUM.在数据样本少时，可以如此确定聚类簇数，当样本空间无限增大，此方法不稳定.所以，此种情形下，当n=1时，划分不合理.

（2）当n＞1时，若，则划分太细，各划分内的样本差异性不大，易造成误判，在样本空间数量较小时，尤其严重；若，说明样本划分过于粗糙，各划分内部没有突出类别特点，使各个子图层次结构复杂，又显混乱，在样本空间较大时，尤为明显.

定义6在定义5基础上，每个划分中，第一个超出各层平均节点个数Ti（i=1，2，…，n）的层命名为质心首层.

定理2离Pi越远，层级越低，若与Pi不属于同一类，则，根据定义6，节点必在质心首层之下.

证明采用反证法，设某节点平行于或高于质心首层，那么，此节点距离Pi较近，距离近，说明两者属于同一类，与条件矛盾，所以该节点与Pi不属于同一类.

定理3最高层与Pi必属于同一类.

证明采用反证法，假设最高层属于多个类，令U11，…，U1n1，为一类，U1n1+1，…，U1n2为一类，U1n2+1，…，U1n3为一类…，那么，说明Pi与多个类都相近，若从数值上考究，说明Pi处于所有类别的交汇点，即Pi属于公共点，而在定义中，不涉及公共点问题，即只能说明Pi为噪声点，噪声点应该被剔除，除此以外，别无其他可能，所以，最高层当属同一类，否则与定义不符.证毕.

1.3 算法复杂度分析

算法复杂度主要包括时间复杂度及空间复杂度，对于N个样本，d个指标的数据集，时间复杂度计算如下.

1.2 节中步骤1至步骤4，基本为线性运算，所以，时间复杂度为O(d◦N)，步骤5中，算法复杂度为O(d◦N2)，步骤6至步骤11，时间复杂度为O(d◦N)，步骤12重复之前的过程，根据划分情况，可估算出其重复次数不超过 logd(N)，所以，算法总复杂度为

空间复杂度计算过程主要采用矩阵运算，矩阵阶数就是样本数，因为主要是进行样本比较运算，若划分为P类，则空间复杂度为

2 算例分析

2.1 多准则汇总及聚类

经过与对多名业务主管的交流，得知目前银行贷款类业务主要在如下几方面进行考核，考察准则如下.

（1）抵借比为欠款额与抵押物估值之比，值越大越不好.权重为ω1.

（2）抵押物价格波动比例系数为价格波动率的倒数，如果升值，价格波动率大于1，如果贬值，价格波动率小于1.可根据需要，每月统计1次，值越大越不好.权重为ω2.

（3）担保方代偿能力为还款额与担保方月收入之比，值越大越不好.权重为ω3.

（4）还款能力为还款额与贷款方月收入之比，值越大越不好.权重为ω4.

（5）发生不可抗力情况损失率为损失额与资产总额之比，值越大越不好，比如各类灾害等.权重为ω5.

（6）贷款比率为贷款总额与现贷款之比，即（现贷款与其他贷款之和比现贷款，如果没有其他贷款，此指标值为1，否则大于1，比值越大越不好.权重为ω6.

（7）资产负债率由专业评估机构核实并给出，数值越大越不好.权重为ω7.

（8）企业效益增长比率为上一个月收入与当前月收入之比，此指标反映企业经营状况，因为企业经营情况跟季节等因素有关，所以这项指标可信度最低.权重为ω8.

将各类贷款人汇总到一起，采用8项指标.根据以上指标，某商业银行提供的数据见表1、表2.

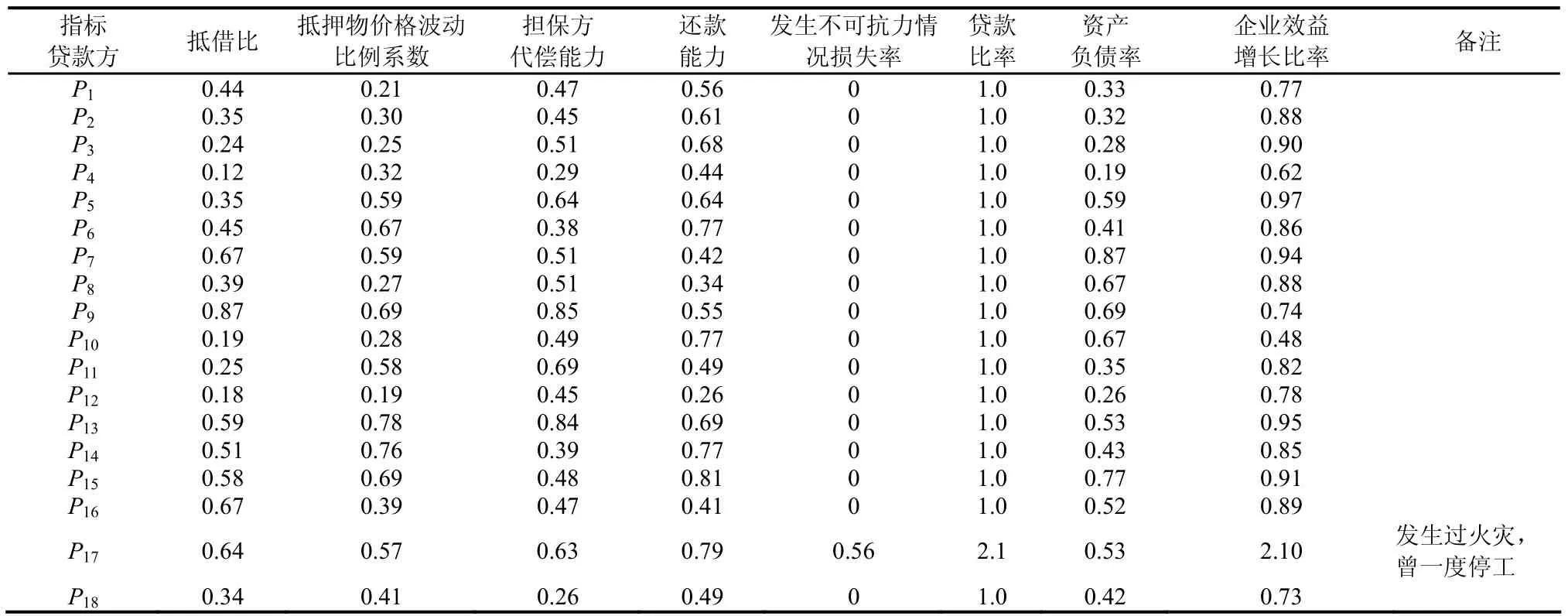
表1 某商业银行2018年7月贷款方考核数据（部分数据） Tab.1 creditor assessment data of a commercial bank in July 2018 (partial data)

表2 某商业银行2018年8月贷款方考核数据（部分数据） Tab.2 creditor assessment data of a commercial bank in August 2018 (partial data)

依据此权重顺序进行偏序集层次聚类.

步骤1指标权重最大的是第4项，贷款人还款能力，依据该指标对表1进行排序.

步骤2将步骤1结果等分成2份，即两个划分.分别为（P12，P8，P16，P7，P4，P11，P18，P9，P1）和（P2，P5，P3，P13，P6，P10，P14，P17，P15）.

步骤3任选一个样本，以P12为例，在其所在划分中将其删除.

步骤4计算P12与各个划分中所有样本对应指标之差，并求出平方，进而绘制哈斯图，如图1、图2.

图1 哈斯图1 Fig.1 Hasse graph 1

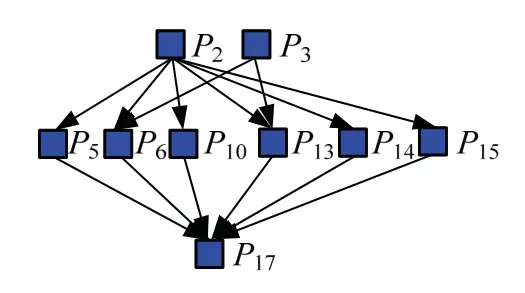
图2 哈斯图2 Fig.2 Hasse graph 2

步骤5计算步骤4中，每个哈斯图各层平均节点个数Ti，求出超过Ti的层次个数SUM，即SUM=3

步骤6计算最佳划分数，， 所以n=2为最佳划分，即这些数据应该聚为2类.

步骤7逐层聚类.

步骤8通过哈斯图节点合并，得到P1、P2、P3、P4、P8、P12、P16为一类，P5、P6、P7、P10、P11、P13、P14、P15、P18为一类，P17属于异常点，与实际相符.

由以上实例可知，利用偏序集实现层次聚类，效果较好.

2.2 呆账风险识别

通过哈斯图可展现各类借款（贷款）人聚类状态，依据层次信息，对债务人进行考察.根据数据业务规模，可以通过单个或多个哈斯图展现.文中算例数据规模较小，所以，所有节点都汇聚在一个哈斯图中.

根据表1，汇总出哈斯图3.根据表2，汇总出哈斯图4.从图4中可以看出，P1节点层次发生了变化，虽然其仍按时还款，但根据图4，可以评估其还款能力发生了变化，经过调研发现某债务人因病住院导致公司业绩受损.所以，当节点层次发生变化时，金融部门工作人员应该引起警觉，如果连续数月对应节点所在层次仍然不能回落到初始状态层次，则其欠款很可能会退变为呆账.后来此债务人公司倒闭，抵押物变卖用于治疗疾病，这导致了呆账形成.通过此例，可以总结出利用偏序集进行层次聚类，能够应用于风险识别.

图3 基于偏序集的2018年7月贷款方考核数据聚类哈斯图 Fig.3 clustering Hasse graph of creditor assessment data based on partial order set in July 2018

图4 基于偏序集的2018年8月贷款方考核数据聚类哈斯图 Fig.4 clustering Hasse graph of creditor assessment data based on partial order set in August 2018

3 结论

（1）构建了基于层次聚类算法的多准则决策模型.通过划分格，可得到最佳分类数，根据分类数，将决策结果划分层次，由层次信息，可得到最优解集.对关系矩阵运算，生成哈斯矩阵，可得出类与类之间的层级关系，也可得出样本间的层级关系.通过偏序集，可以快速准确实现层次聚类，较传统聚类方法方便快捷，计算量少.

（2）传统聚类过程中，利用不同的距离公式得到不同的聚类结果，距离计算会增加时间复杂度.而利用偏序集原理实现的聚类，可以仅通过比较关系得到种类归属，时间复杂度及空间复杂度大为降低，通过层次关系找到种类归属.今后，拟利用偏序集原理实现更多聚类算法.