流动性视角下波动率指数期货定价：基于HAR模型的直接定价法

苏乐怡， 乔高秀， 蒋龚月

（西南交通大学数学学院，成都 611756）

流动性是金融市场中的重要指标，是市场微观结构的重要变量.尽管市场流动性与波动率属于不同的维度，但它与波动率之间仍然存在信息交互，有着密切的联系.近年来，已经有大量文献研究了含有流动性因素的资产定价，均得到了实证结果的支持［1-3］.因此，无论从理论分析还是实证结果来看，流动性都是资产定价的一个非常重要的影响因素.然而现有研究主要是基于股票市场，相比之下，研究流动性对金融衍生品价格影响的文献较少.Chou 等［4］使用隐含波动率衡量期权价格结构，研究了流动性对期权价格的影响.Zhang等［5］提出了一种新的衍生品定价模型，并发现在对石油和黄金的定价方面加入流动性的模型比基准模型更加准确.

1993 年，CBOE 开始编制VIX 指数，经过十几年的发展，VIX 指数逐渐得到了金融市场的认同.2004 年3月26日，CBOE基于VIX指数推出了VIX期货合约，这一全新的金融产品成交量不断地攀升，交易品种也越来越丰富.Zhang和Zhu［6］最早基于连续时间模型研究了VIX期货定价.Kanniainen等［7］将股票收益率和风险中性信息加入到了估计参数的似然函数中，实证表明在目标函数中包含风险中性信息可以提高参数估计的精度，获得更好的定价性能.Wang 等［8］基于离散时间模型HN-GARCH 推导出了VIX 期货的定价公式.VIX期货定价逐渐得到研究者们的广泛关注［9-11］.

近年来，已实现波动模型的使用频率越来越高，其中最有代表性的模型是异质自回归（HAR）模型.已有研究表明HAR类模型可以很好地匹配期权价格的隐含波动信息［12-13］，他们对HAR模型进行了拓展（分别为HARG 和LHARG），后者还推导出了期权定价公式.最近，Huang 等［14］使用Majewski 等［13］提出的拓展模型（LHARG）推导出了不同期限结构下的VIX期货封闭定价公式.与上述通过对最底层标的资产股票价格指数建模来研究VIX期货定价的“间接定价法”研究不同，Yin等［15］使用HAR模型对波动率指数直接建模并推导出VIX期货定价公式.这种建模方法简单易于估计，且具有很高的预测精度，称为“直接定价法”.通过引入其他外生信息对该模型进行扩展，继续深入研究这种“直接定价法”下的VIX期货定价具有重要的理论与应用价值.实际上，流动性是影响衍生品价格的一个不可缺少的维度，然而尚无文献探讨流动性对波动率衍生品价格的影响，本文将从这一角度对已有研究进行补充.

本文主要探讨代表市场微观结构的流动性对VIX期货价格的影响机制.在定价方法上，基于异质自回归模型（HAR模型）提出波动率指数（VIX）期货的直接定价法，假设在风险中性测度下对数VIX遵循HAR模型，滞后一天的对数流动性作为外生变量加入HAR模型中.由于流动性自身的自相关性也很强，本文假设流动性也服从HAR模型的设定形式.另外，又采用了间接定价法中受到广泛使用的HN-GARCH模型来比较两种不同方法下的预测性能.本文的建模方式不仅充分考虑了市场微观结构信息流动性的影响，同时与间接定价法对最底层标的资产建模相比也有效地简化了定价过程.本文研究为我国衍生品市场保持高效运行与正常的功能发挥提供有效信息，也为深入研究“金融化”市场下期货定价和运行机制带来一些经验.

1 模型

1.1 流动性测度

流动性对投资者极为重要，然而它具有不可观测性，因此有很多学者从不同角度提出了各种流动性的度量指标.Amihud［16］在研究美国证券市场时开发出了一种非流动性指标，将其定义为每日日间的绝对收益与当日交易量之间的比率.本文将采用这种方法计算非流动性，定义如下：

其中：ILLIQt表示S&P 500 指数在第t天的非流动性；Rt表示S&P 500 指数第t天的对数收益率；Vt表示S&P 500指数第t天的交易量.

1.2 基于HN-GARCH模型的VIX期货定价

HN-GARCH模型是由Heston和Nandi［17］提出的.在物理测度P下，假定S&P 500指数日收益表示为：

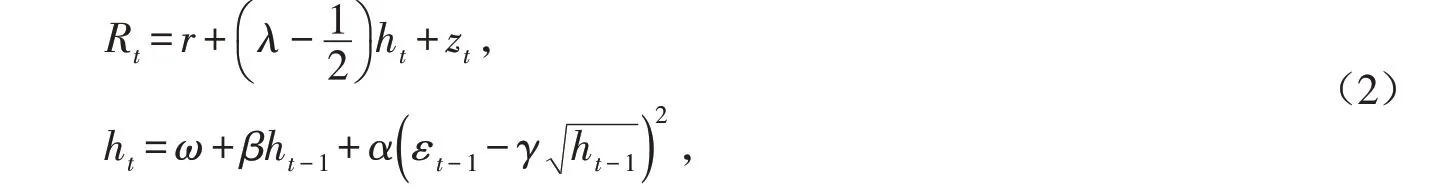
其中：Rt代表日收益率；r代表无风险利率；λ是与条件方差ht相关的股权风险溢价，λ>0；zt=ht εt，εt∼iid N( )0,1 ；ω，β，α与γ均为自回归参数，满足条件：ω>0，α，β≥0，γ>-0.5.

风险中性测度Q下，模型表示为：

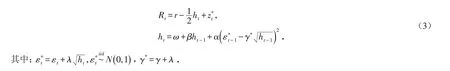
风险中性测度Q下条件方差满足：

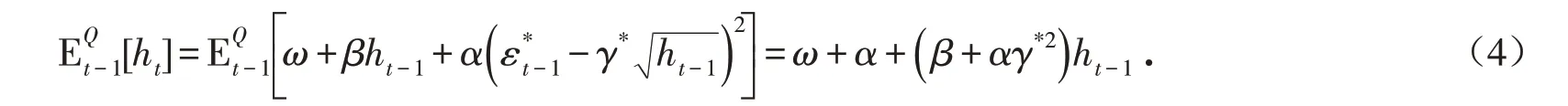
令Ω*=ω+α>0，Γ*=β+αγ*2，其中Γ*表示风险中性下条件方差的持久性且满足Γ∗<1，风险中性的长期

Hao和Zhang［18］证明了该模型隐含的VIX是HN-GARCH模型下条件方差的线性函数，其线性关系满足

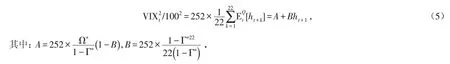
Wang等［8］提出了基于HN-GARCH模型的VIX期货定价公式，第t天到期时间为T的期货价格为

可以推导出

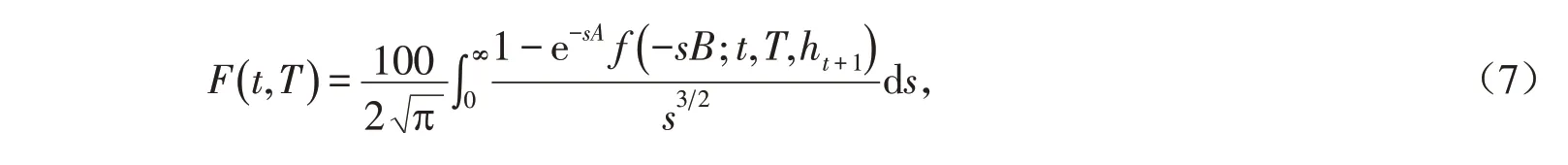
其中f( )ϕ;t,T,ht+1是条件方差ht+1的矩母函数，表示为

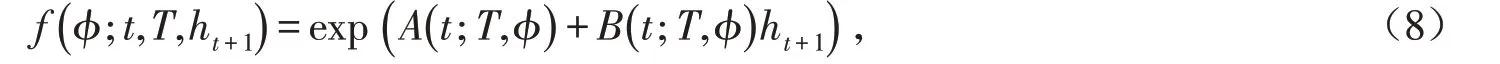
简记为：At=A(t;T,ϕ)，Bt=B(t;T,ϕ).其迭代关系满足：

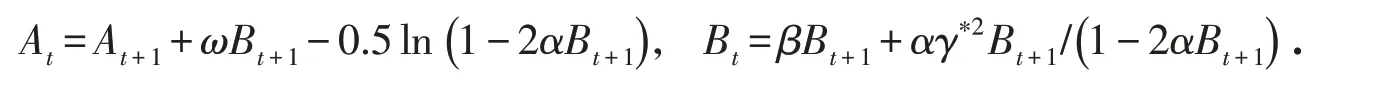
终值条件为：AT=0，BT=ϕ.证明过程见Wang等［8］.

1.3 基于HAR模型的直接定价法

HAR模型通过波动率自回归过程描述了不同时段的异质交易行为.假设对数VIX遵循HAR框架.由于VIX指数本身代表了风险中性的波动率，则对VIX指数建模意味着直接在风险中性测量下的建模.在风险中性测度下，HAR模型表示为

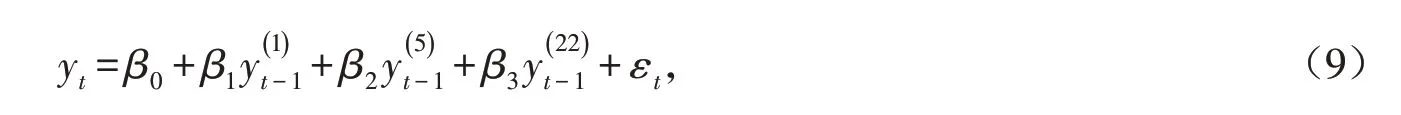
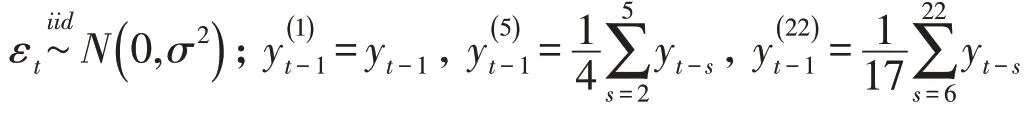
根据Carr和Wu［19］的研究，期货价格表达式如下：

可以证明，在HAR模型下VIX期货满足以下形式：

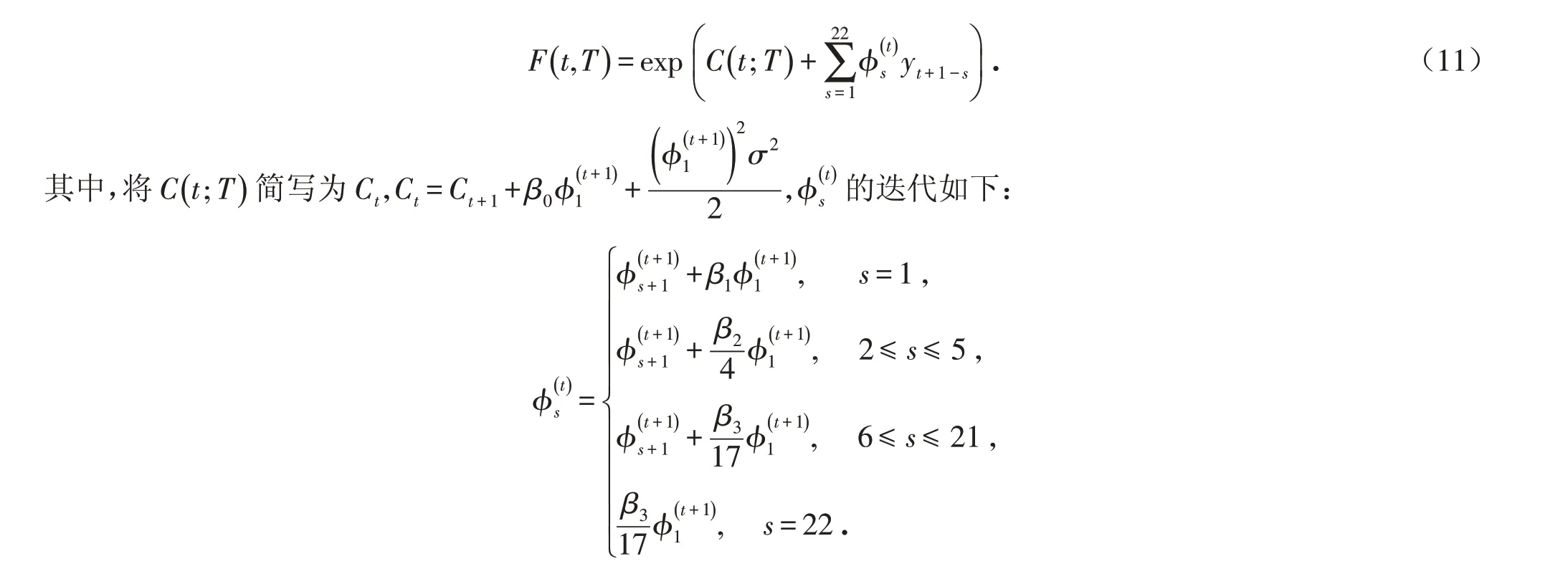
终值条件满足：CT=0，ϕ=1，当s>1时，ϕ=0.证明过程如下：

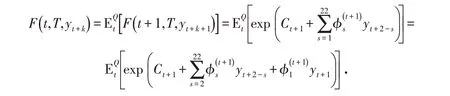
所以有：

因此，

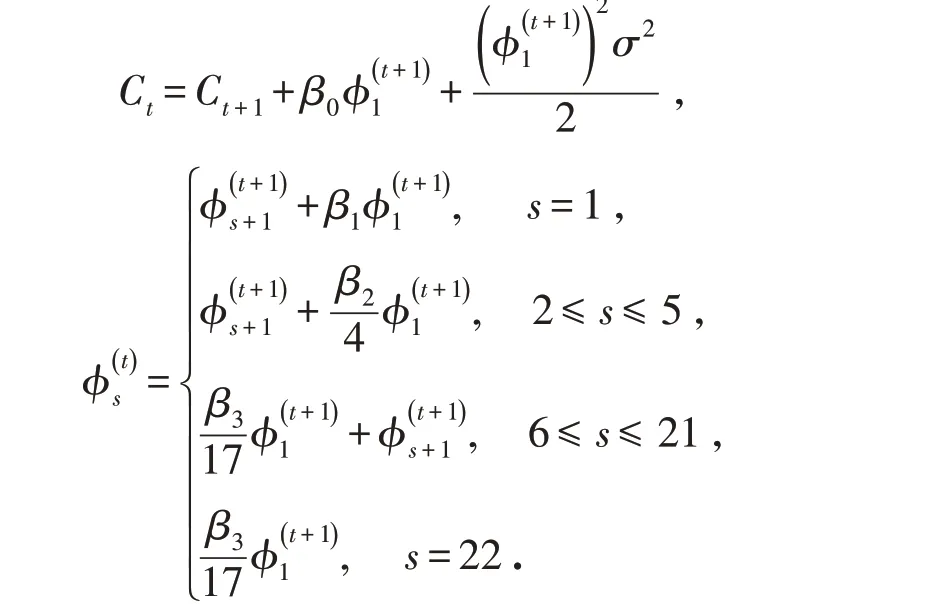
1.4 流动性视角下基于HAR模型的直接定价法

本节将流动性作为外生变量加入模型中：假设流动性在风险中性测度下也服从HAR模型的设定形式，并将滞后一天的流动性加入方程（9）中，记为HAR-LIQ模型，表示如下：

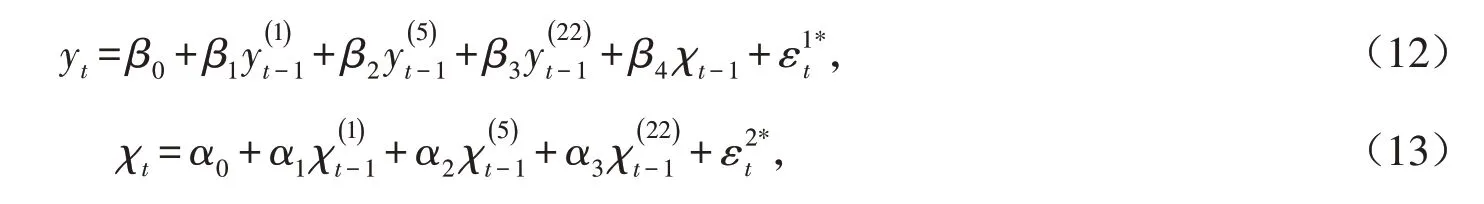
根据Carr和Wu［19］的研究，期货价格表达式如下：

可以证明，在HAR-LIQ模型下VIX期货满足以下形式：

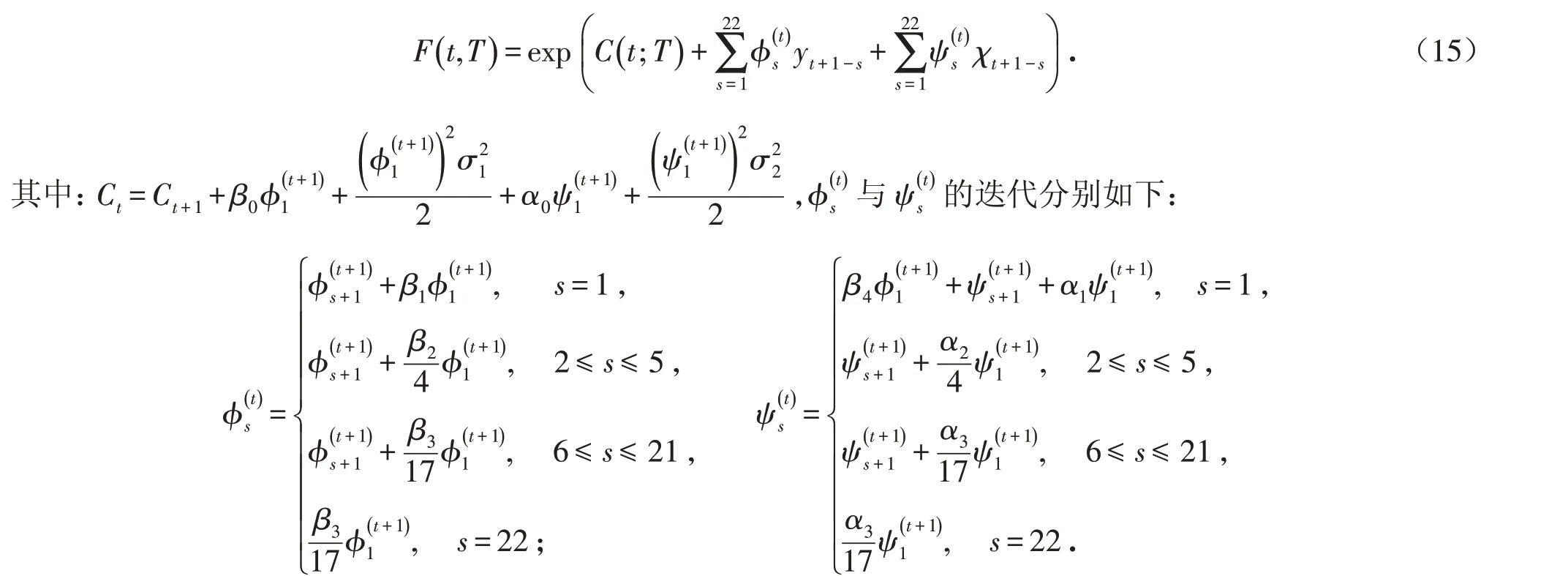
终止条件满足CT=0，ϕ=1，当s>1时，ϕ=0，ψ=0.证明过程如下：

所以有：

因此，

2 研究方法

2.1 估计方法

本文用仅含VIX 期货信息的极大似然函数对参数进行估计，并将这种估计方法称为仅“VIX 期货”法.似然函数如下：

2.2 估计误差

为了衡量模型的预测能力，本文采用了四种损失函数：MAE、RMSE、MAPE和QLIKE.计算如下：

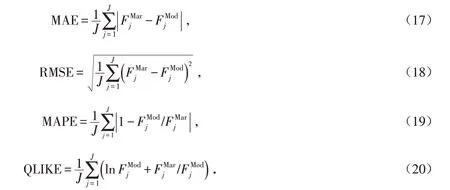
其中：F表示VIX期货的真实值；F表示VIX期货的预测值；J为预测样本的长度.

3 实证结果

3.1 数据

本文收集了S&P 500 指数来计算非流动性指标，数据来源于雅虎财经.VIX 指数数据以及VIX 期货数据来源于CBOE网站.样本期从2004年3月31日至2019年12月31日，删除所有到期时间超过2019年12月31 日的期货合约，最终样本共27 561个价格.根据之前的研究［8-9］，VIX期货价格采用了多个过滤器.首先计算每个交易日期货合约的到期日，并删除所有到期日小于5 d的合约，为了避免流动性偏差，删除未平仓量小于200的合约价格，并用日结算价作为期货价格的表示.为了检验模型的预测能力是否与到期时间长短有关，本文将VIX 期货分为三组，分别为：T≤60，60120，它们分别代表短期、中期和长期的VIX期货合约；由于VIX期货价格通常也反映了VIX指数未来的市场预期，所以按照VIX指数水平将VIX期货分为三组，分别为：VIX ≤15，1520.

表1为所有数据的描述性统计，分别采用格兰杰因果关系检验法与皮尔逊相关系数来检验VIX指数与Amihud非流动性之间的因果关系以及相关性.Amihud非流动性、VIX指数和VIX期货的峰度分别为18.984 1、10.267 9和4.187 0，均偏高.VIX期货随着到期时间的增加，均值有所增加，方差和偏度峰度都有所降低，最大值降低而最小值增加；VIX期货随着VIX指数的增大，除了峰度以外的其他描述统计量均随着增加.值得注意的是，在1%显著性水平下，Amihud非流动性构成VIX指数的Granger成因，而VIX指数不构成Amihud非流动性的Granger成因.此外，VIX指数与Amihud非流动性的皮尔逊相关系数为0.344 4，呈正向弱相关.

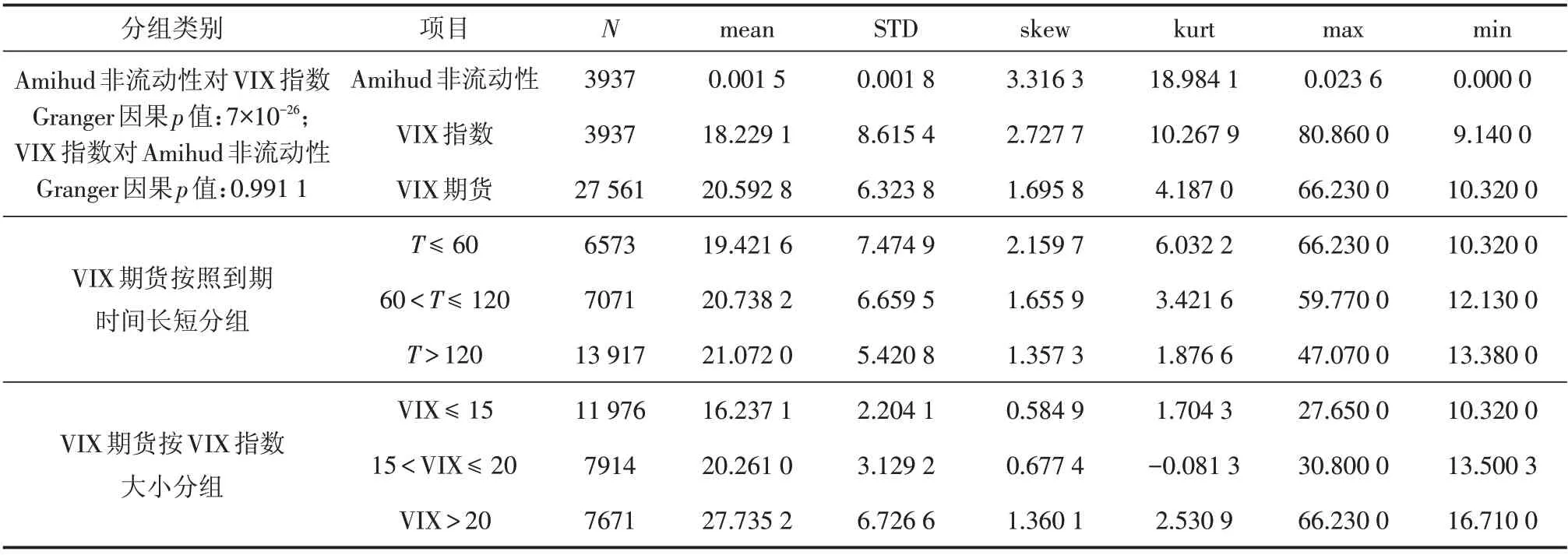
表1 描述性统计Tab.1 Descriptive statistics

由于样本量较大，包含了2008—2009年金融危机期，所以本文的研究将全体样本分为两组，2004年3月31日至2011年12月31日为第1组，2012年1月1日至2019年12月31日为第2组.

图1 和图2 分别展示了VIX 指数和Amihud 非流动性随时间的演变.可以看出，在2008 年金融危机期间，随着波动率的大幅度提高，流动性水平也出现了极高的波动，它们在经历了这段不稳定的时期之后均处于相对较低的水平.

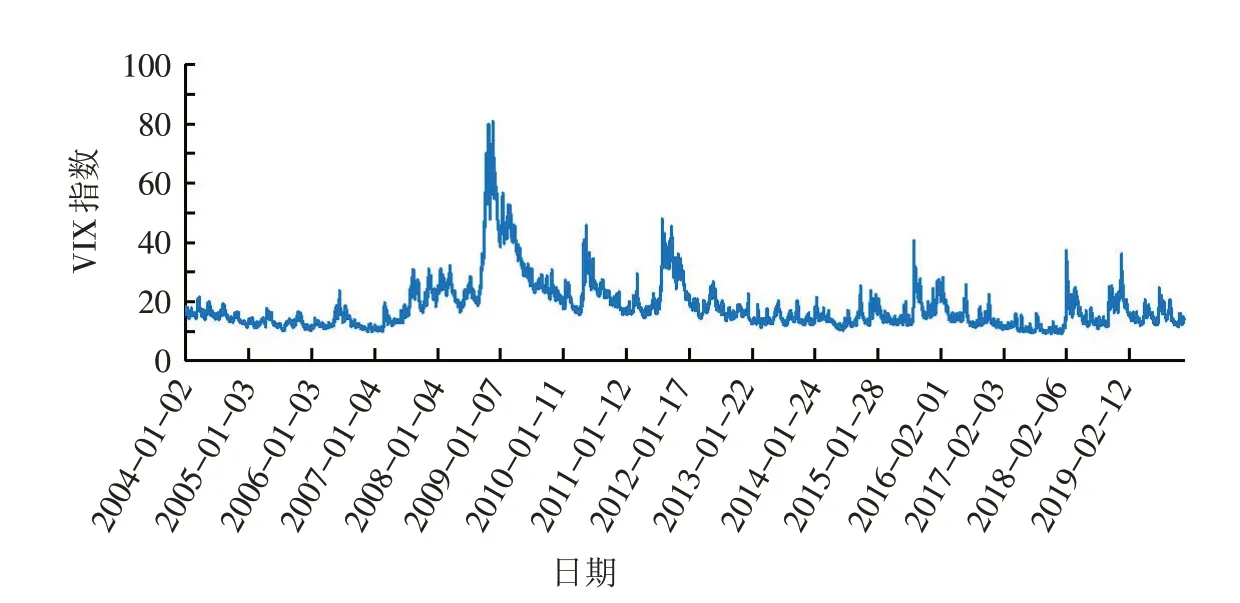
图1 VIX指数Fig.1 VIX Index

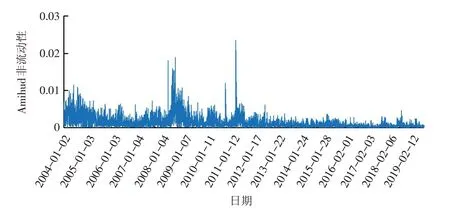
图2 Amihud非流动性Fig.2 Amihud illiquidity

表2展示了Amihud非流动性的回归分析结果.α2和α3均在1%显著性水平下显著，说明滞后的非流动性对当前非流动性起到了预测作用.基于此，本文将滞后一天、一周和一月的流动性保留在流动性的回归模型中.

表2 Amihud非流动性的回归分析结果Tab.2 Regression analysis results of Amihud illiquidity

3.2 参数估计

本节将使用极大似然法拟合本文中的回归模型来估计参数，表3、表4报告了HN-GARCH模型、HAR 模型以及HAR-LIQ 模型的样本内参数估计结果.

从表3 中可以看到，HN-GARCH 模型在两个子样本估计下的β值都接近1，持久性Γ*也都接近1，表明风险中性动态导致了更高的持久性.

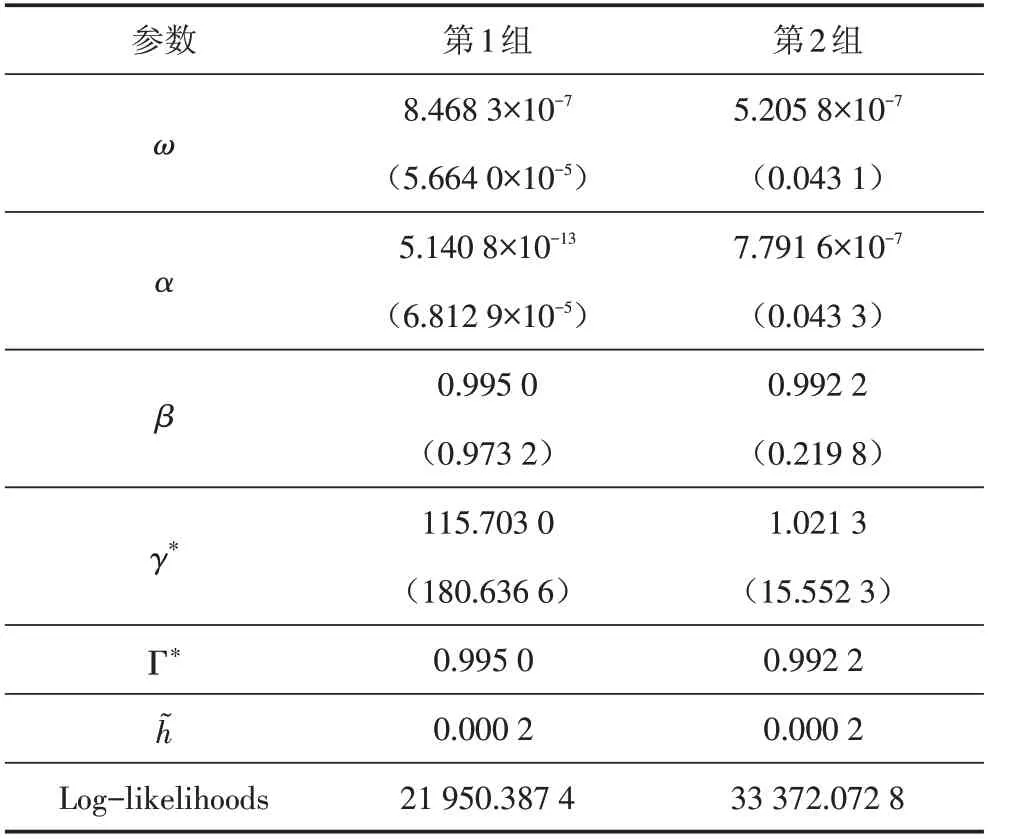
表3 HN-GARCH模型样本内参数估计结果Tab.3 In-sample parameter estimation results of HN-GARCH model

从表4中可以看到，HAR和HAR-LIQ两模型的回归系数均为正，其中滞后一天的回归系数β1最大，对VIX指数的预测发挥了最大的作用；滞后一周与滞后一月的回归系数较小，在一些样本的估计中趋于零，且滞后一月系数β3均大于滞后一周系数β2，表明滞后一月的VIX指数比滞后一周的发挥了更大的作用.其中第1组的系数β1小于第2组的β1，而第2组滞后多阶的系数更小，表明第2组VIX期货预测更依赖于近期的VIX指数.另外，HAR-LIQ模型的似然函数均大于HAR模型的.

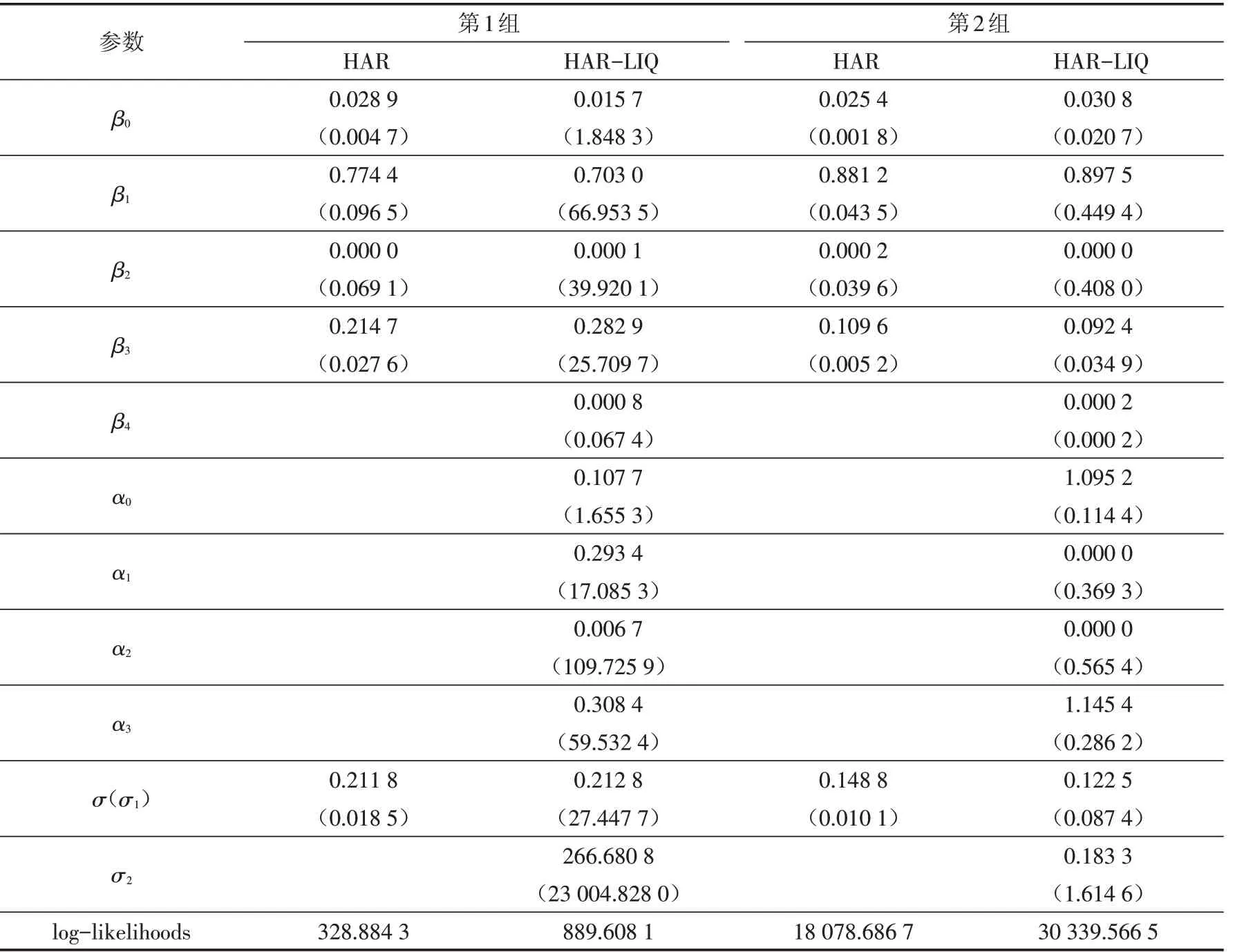
表4 HAR和HAR-LIQ模型样本内参数估计结果Tab.4 In-sample parameter estimation results of HAR model and HAR-LIQ model

3.3 样本内外定价误差

本节报告了两个子样本的样本内外定价误差分析.表5为三个模型的总样本预测结果，从表中可以看出，在第1 组样本内外，HAR 模型和HAR-LIQ 模型的预测结果均优于HN-GARCH 模型；在第2 组样本期，HAR 模型和HAR-LIQ 模型在样本内定价效果更好，而HN-GARCH 模型在样本外的定价效果更好.对于HAR模型，在四种不同误差评估标准下，流动性的加入在两个子样本内外均降低了对VIX期货的定价误差.

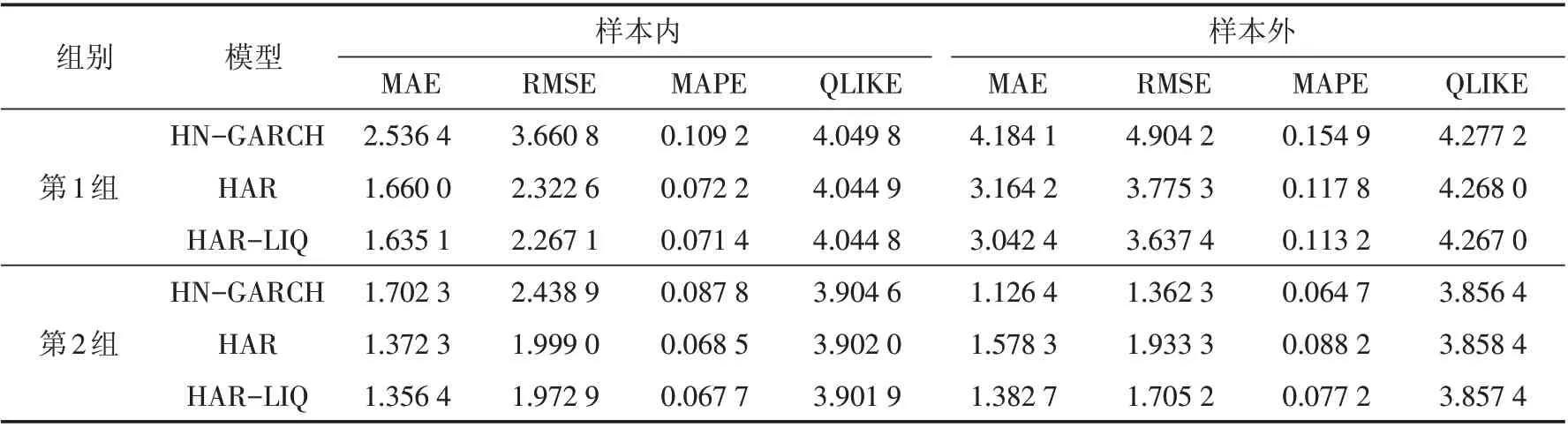
表5 VIX期货样本内和样本外定价误差Tab.5 In-sample and out-of-sample pricing errors of VIX futures

表6和表7分别报告了三个模型按照到期时间和VIX指数大小分组的定价误差.从样本内表现来看，在两个子样本中，不同到期时间以及VIX指数水平下，HN-GARCH模型的定价误差均大于HAR和HAR-LIQ模型，这一结果与表5 中总定价误差一致.进一步分析可以发现，在第1 组中，HAR-LIQ 模型对长期期货（T>120）的定价误差低于HAR模型，对于中短期期货（T≤120）的预测只有RMSE函数低于HAR模型.但对于不同VIX 指数水平，HAR-LIQ 模型的四种误差函数均低于HAR 模型；在第2组中，HAR-LIQ 模型在不同长度的到期时间下定价误差均低于HAR模型，且除了对VIX ≤15 的情况外，其他两个VIX指数水平分组下HAR-LIQ模型定价误差也均小于HAR模型.

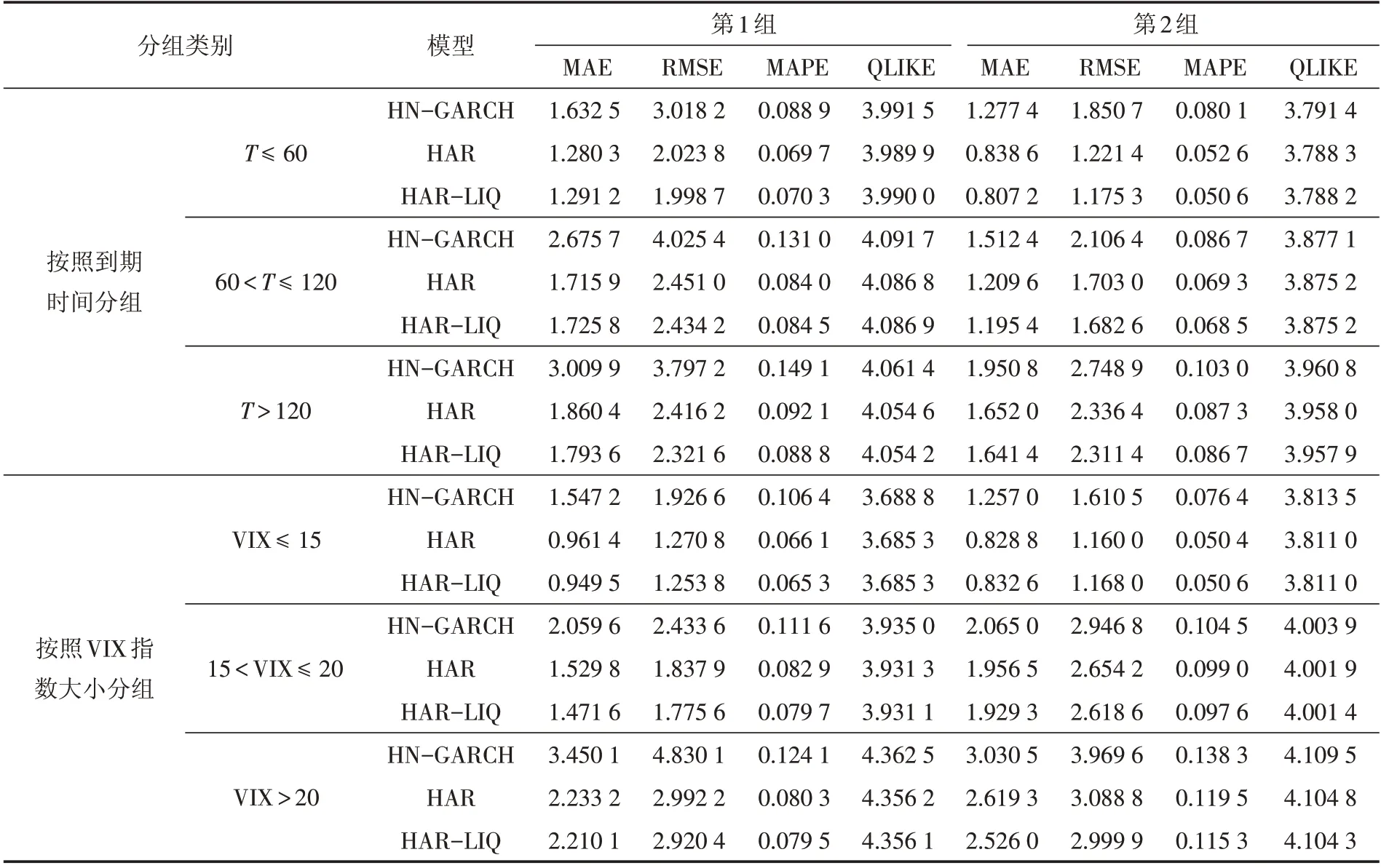
表6 VIX期货样本内定价误差分组结果Tab.6 Grouping results of in-sample pricing errors of VIX futures

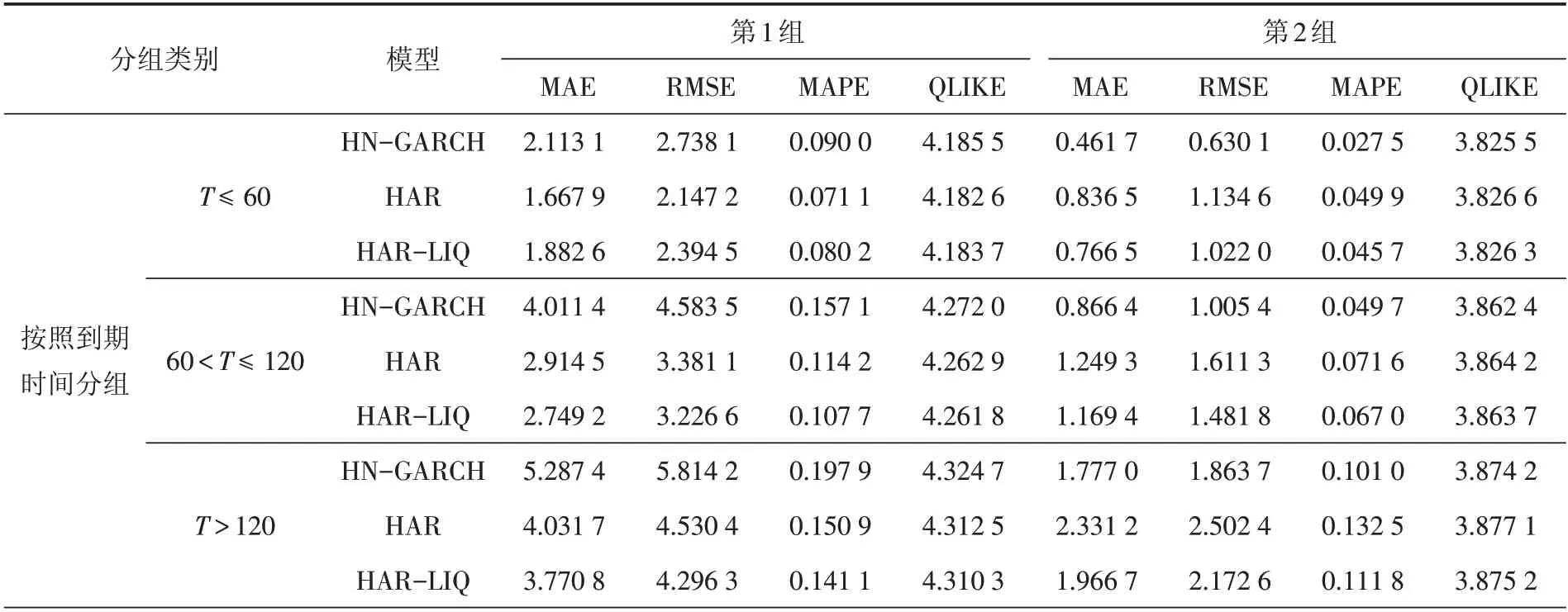
表7 VIX期货样本外定价误差分组结果Tab.7 Grouping results of out-of-samples pricing errors of VIX futures

续表

从样本外的表现可以发现，第1组样本外中，不同到期时间以及VIX指数水平下，HAR模型和HAR-LIQ模型的定价误差更小，而第2组样本外中，只有在VIX ≤15 的样本中HAR模型和HAR-LIQ模型定价误差小于HN-GARCH模型，其余分组中HN-GARCH模型的定价误差更小.进一步分析可以发现，第1组对于短期VIX期货（T≤60）的预测中，HAR-LIQ模型定价误差大于HAR模型，然而对其他任意到期时间以及VIX指数水平来说，HAR-LIQ模型的定价误差均小于HAR模型的，相对于HAR模型有效降低了定价误差.总体来看，流动性的加入稳定地提高了HAR模型对VIX期货的样本外预测能力.

为了进一步探究HAR 模型和HAR-LIQ 模型的定价误差与到期时间和VIX指数水平的关系，本节画出了第2 组样本外中，两模型在三组不同VIX 指数水平下期货定价误差函数（RMSE）随着期货到期时间的变化，如图3所示.

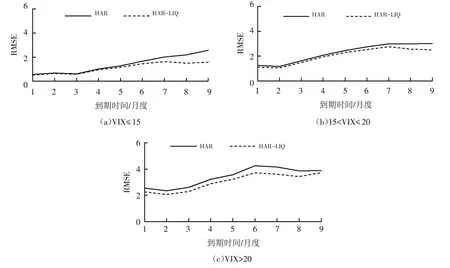
图3 不同波动率下VIX期货样本外定价误差（RMSE）Fig.3 Out-of-sample pricing errors（RMSE）of VIX futures under different volatility levels

可以看到，两模型变化规律相似，呈现出明显的变化趋势：随着到期时间的增加定价误差函数RMSE也增大，且随着VIX指数的增加定价误差函数RMSE也明显增大.HAR-LIQ模型的定价误差函数RMSE总是小于HAR模型的误差，在VIX ≤15 和1520 下的定价误差随着到期时间的增加变化平均，表现出了比较明显的优势.

4 结论

本文基于异质自回归模型（HAR模型），将市场微观结构重要指标——流动性加入模型中，采用直接定价法研究模型定价性能，并与采用间接定价法的HN-GARCH模型进行了比较.相比之下，本文提出的新模型在充分引入有效金融市场信息的同时大大简化了定价过程.更重要的是，流动性的这种建模方式非常有效，对VIX期货的定价起着重要作用，具体表现为：无论样本内外，在四种误差评估标准下，HAR-LIQ模型的VIX期货定价表现均优于HAR模型.这为我国研究衍生品定价和衍生品市场运行机制带来了有效的经验.同时实证结果也表明，HAR模型和HAR-LIQ模型与HN-GARCH模型在不同样本期对VIX期货定价表现有差异，这需要后期对两类的适用情形进行更深入的探讨.