粗糙裂缝压裂暂堵剂运移规律数值模拟

郑 臣，汪道兵，秦 浩，董永存，宇 波

(1.北京石油化工学院 机械工程学院，北京 102617； 2.中国石油化工股份有限公司 济南分公司，山东 济南 250101)

0 引言

水力压裂技术是油气开采过程中的一项重要技术[1]，常规水力压裂存在形成缝网结构单一、开采效率不高等问题。为精准开采更多油气资源，张涛等[1]提出一种向人工裂隙内加入暂堵剂、提高缝网复杂程度的暂堵转向压裂技术。暂堵转向压裂过程中，暂堵剂在裂隙内的运移过程对暂堵转向压裂施工效果起决定性作用[2]。因此，需要对暂堵剂在裂隙内的运移过程有精准的认识。

暂堵剂在裂隙内运移过程的研究方法主要有实验研究和数值模拟研究。暂堵剂在裂隙内运移过程的研究较少，人们将暂堵剂分成颗粒、纤维、冻胶和可膨胀型4类，通过实验研究刻画部分暂堵剂缝内封堵演化规律[3-4]。相关研究对于暂堵剂形成封堵前的运移规律分析较少，由于暂堵剂缝内运移物理过程与支撑剂在裂隙内运移过程相似，可以借鉴部分支撑剂在裂隙内运移过程的研究成果。影响支撑剂在裂隙内运移过程的主要参数包括支撑剂入口位置、支撑剂颗粒直径和注入速度等[5]。将岩石裂缝简化为光滑平行板模型，分析各参数对支撑剂缝内运移过程的影响，认为支撑剂颗粒直径最佳尺寸为100目，颗粒直径增大导致支撑剂沉降速度加快、支撑剂砂堤平衡高度增大；当水平裂缝位置低于入口位置时，支撑剂容易被堵在交叉点，导致支撑剂无法在水平裂缝内形成砂堤[6-9]。

数值模拟研究[10]表明，支撑剂携带液黏度、支撑剂注入速率、支撑剂直径[11-13]、裂隙宽度、主裂隙与二次裂隙之间的夹角和裂隙分支的复杂程度[14-16]是影响支撑剂在裂缝内运移过程的主要参数；支撑剂沉降过程中水平方向初始速度较快，且靠近壁面处的支撑剂颗粒运移速度明显低于裂缝中部的[17]；同时，减小支撑剂的密度能够在一定程度上使输送距离增加，但增加幅度未能达到预期[18]。

笔者构建具有长度相等的阶梯粗糙裂缝物理模型和CT扫描真实粗糙裂缝模型，分析颗粒直径、颗粒体积分数、颗粒速度和暂堵剂携带液黏度等因素对暂堵剂在粗糙裂缝内运移过程的影响，为分析暂堵转向压裂施工过程中暂堵剂在粗糙裂缝内的运移规律提供指导。

1 数值模型

1.1 物理模型

1.1.1 光滑裂缝模型

暂堵剂在暂堵转向压裂工程中的运移过程主要分为两个阶段：第一阶段为暂堵剂在裂缝内运移阶段；第二阶段为暂堵剂封堵裂缝阶段。由于暂堵剂在裂缝内形成封堵前的运移过程与支撑剂在裂缝内运移过程相似，参考支撑剂输送实验，将岩石裂缝等效为光滑平行板模型，作为粗糙裂缝模型进行对比研究(见图1)[18]。建立模型的长度为400 mm，宽度为6 mm，高度为200 mm，左侧为裂缝入口面，右侧为裂缝出口面，其余部分为裂缝壁面，流动方向从左到右。

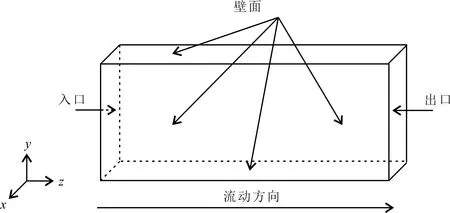
图1 光滑裂缝几何模型示意

1.1.2 粗糙裂缝模型

为符合实际生产情况，在光滑裂缝模型的基础上添加阶梯(表示粗糙裂缝)，阶梯粗糙裂缝物理模型较为简单，可以直观显示裂缝粗糙度对暂堵剂运移规律的影响。单一阶梯粗糙裂缝物理模型的宏观粗糙特征与真实粗糙裂缝存在较大差距，为保证阶梯粗糙裂缝几何模型构建的合理性，通过膨胀致裂实验获得真实粗糙裂缝，利用HandySCAN 3D扫描仪对真实粗糙裂缝表面进行扫描，扫描仪光栅精度为0.025 mm，对扫描数据进行处理获得真实粗糙裂缝物理模型(见图2(a-b))。真实粗糙裂缝中部有明显凸起段，靠近入口和出口位置分布凹陷段，裂缝粗糙特征分布较为规律。因此，预制3个粗糙阶梯，均匀分布在裂缝入口附近、裂缝中部和靠近裂缝出口位置，并且阶梯凸起分布方向相反、高度相同，保证阶梯粗糙裂缝特征分布与真实粗糙裂缝特征分布相似，采取与光滑裂缝模型相同的几何尺寸和网格数量，监测相同的数据进行对比分析，说明粗糙裂缝对球形颗粒暂堵剂在裂缝内运移过程的影响。阶梯粗糙裂缝几何模型见图2(c)，所有转折处的裂缝宽度与光滑裂缝模型的相同。

图2 粗糙裂缝几何模型示意

1.2 离散相模型(DPM)

多相流数值模拟方法有欧拉—拉格朗日和欧拉—欧拉两种。离散相模型(DPM)采用欧拉—拉格朗日方法，将流体处理成连续介质，在基于欧拉思想的网格下求解Navier-Stokes方程，完成对连续相的描述；将颗粒相处理成离散单元，在基于拉格朗日思想的网格下，通过牛顿第二运动定律求解每个颗粒的速度、受力和位置等信息，完成对颗粒相的描述。连续相和离散相采取双向耦合的方式进行耦合计算，过程：(1)设置连续相和离散相相关参数；(2)进行连续相的计算，得到连续场；(3)再考虑连续场对离散相影响的基础上，计算离散相，得到单向耦合场；(4)将单向耦合场的影响作用到连续相，进行连续相计算，得到双向耦合场；(5)交替计算连续相和离散相方程，得到收敛的耦合解。基于DPM多相流模型的CFD双向耦合流程见图3。

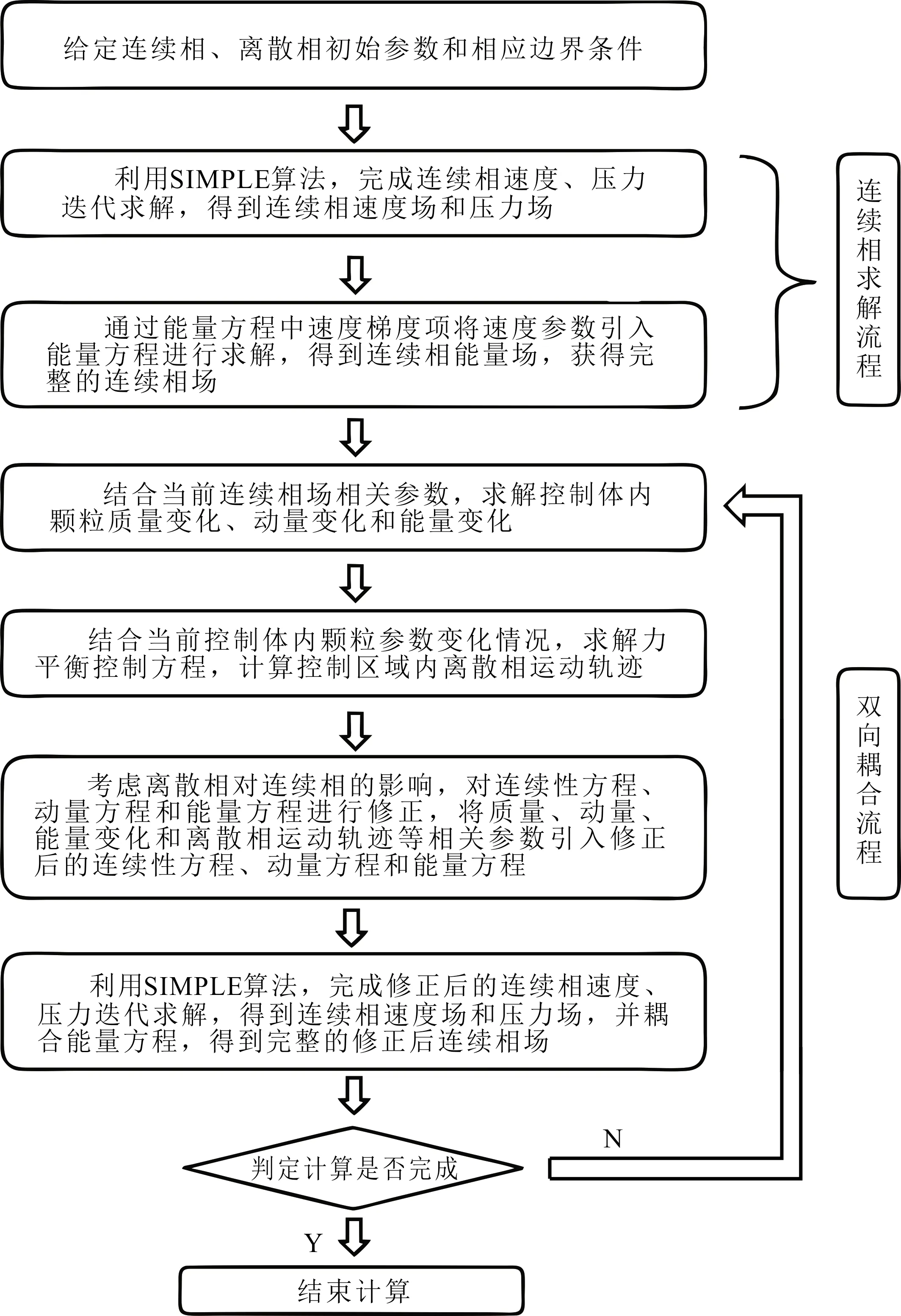
图3 基于DPM多相流模型的CFD双向耦合流程

1.3 数学模型

计算数学模型包括3个部分，分别为连续相数学模型、离散相数学模型和交叉耦合方程。

1.3.1 连续相数学模型

在DPM方法中，流体运动在欧拉坐标上求解，采用质量守恒方程和动量守恒方程，质量守恒方程为

(1)

式中：Sm为源项，表示离散相添加到连续相中的质量，或其他任何需要考虑到连续相中的相；ρ为流体密度；t为时间；为拉普拉斯算子；v为流体速度。

动量守恒方程为

(2)

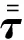
(3)

式中：μ为流体黏度。

1.3.2 离散相数学模型

利用牛顿第二定律对离散相进行力平衡积分，计算暂堵剂的运动轨迹，表达式为

(4)

(5)

(6)

式(4-6)中：mp为暂堵剂质量；vp为暂堵剂速度；ρp为暂堵剂密度；dp为暂堵剂直径；τr为暂堵剂弛豫时间；Re为雷诺数；Cd为常数，取0.5。

质点旋转是质点运动的自然组成部分，对质点在流体中的运动轨迹有显著影响。如果在模拟研究中忽略粒子的旋转，得到的粒子轨迹与实际粒子轨迹有很大的不同。为考虑质点旋转，求解质点角动量的附加常微分方程为

(7)

(8)

(9)

式(7-9)中：T为力矩；ω为流体与暂堵剂之间的相对角速度；Ip为惯性矩；ωp为暂堵剂角速度；Cω为旋转阻力因数。

1.3.3 交叉耦合方程

流体与暂堵剂之间存在相互作用，考虑流体对暂堵剂的影响，质量交换表示为

(10)

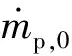
动量交换表示为

(11)

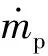
考虑暂堵剂对流体的影响，改写连续性方程、动量方程[10]，添加暂堵剂相关信息，刻画暂堵剂对流体影响过程，暂堵剂对流体的影响通过修正的连续性方程、动量方程进行求解。

连续性方程改写为

(12)

式中：αp为暂堵剂体积分数；mlp为流体到暂堵剂的质量传递；mpl为暂堵剂到流体的质量传递。

动量方程改写为

(13)

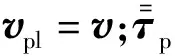
(14)

2 网格无关性及算例验证

2.1 网格无关性验证

物理模型几何结构较为规则，为提高计算速度，采用六面体网格单元进行计算，网格单元长度为1 mm。验证光滑模型和粗糙模型网格无关性，证明计算结果没有受到网格数的影响，一般工程应用认为两次验证结果相对误差应在5 %以内[19-21]。对网格进行均匀加密，在入口面和出口面中间位置各绘制一条直线，监测压力变化，计算结束取平均值代表该面的压力，并将入口面和出口面的平均压力相减，得到压力差。模型较为简单，40×104网格数为较大网格密度，压力差为相对精确解。网格数需倍数增加，分别计算5×104、10×104和20×104网格数的压力差，分别与40×104网格数的压力差作比较，其表达式为

(15)

式中：ΔpE为不同网格数的压力差与40×104网格数的压差之间的相对误差，Δp为不同网格数的压力差，Δp0为40×104网格数的压力差。

网格误差变化曲线见图4。由图4可以看出，随网格数的增加，计算误差逐渐减小。网格加密方式较为均匀，呈现较好的计算效果，误差小于1.0 %。对于光滑模型，当网格数较少时，计算误差较大，接近10.0%，在网格数达到10×104时，计算误差小于5.0%，达到工程应用要求。当网格数量再次增加时，计算误差变化不大。因此，选择光滑模型和粗糙模型网格数为10×104进行对比。

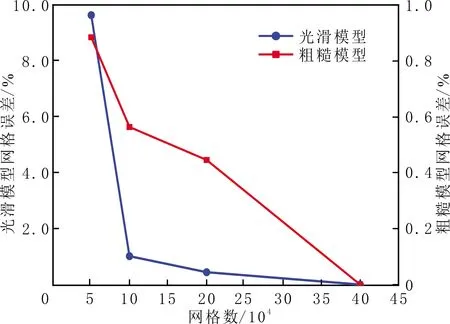
图4 两种模型网格误差变化曲线

2.2 算例验证

为确保数值模拟正确性，需要排除网格数对计算结果的影响，并对算例进行验证。将文献[22]的模拟结果进行复现。基于PM2.5/PM10浓度检测系统，检测池中形成的流体系统为气—液—固多相流系统，属于小尺度模型，模拟精度要求较高且含固体颗粒的体积率较小，在不考虑气泡因素影响的情况下，利用DPM多相流模型对固—液两相流中的微颗粒运动特性进行数值模拟[22]。选择单独颗粒运动轨迹作为对比，数值模拟数据与文献[22]轨迹对比见图5。由图5可以看出，蓝色轨迹线和红色轨迹线基本重合，最大误差小于4.2%，验证算例结果基本正确。

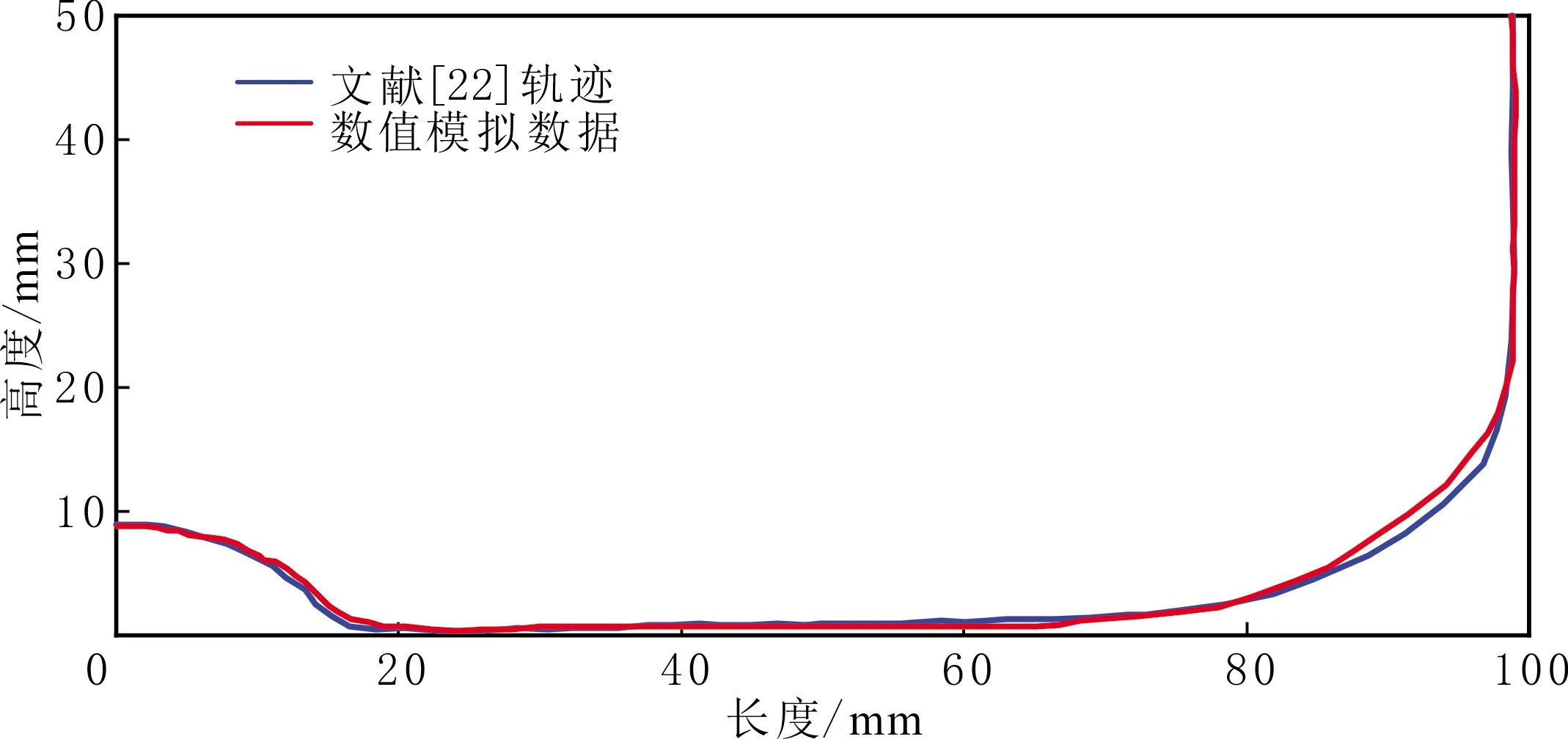
图5 数值模拟和文献颗粒轨迹

3 数值模拟方案

将划分的计算网格读入ANSYS FLUENT软件进行计算，利用DPM多相流模型进行球形颗粒暂堵剂在裂缝内的运移过程的数值模拟。该模型可以考虑颗粒之间相互碰撞的影响，入口边界条件为速度型入口，出口边界条件为压力型出口，设置壁面边界条件光滑且无滑移，当颗粒与壁面接触时对颗粒进行反射，采用矩形阶梯状凸起表示粗糙壁面。计算参数见表1-2。

表1 计算参数

表2 边界条件

利用控制变量法，分析暂堵剂缝内运移过程参数敏感性，自变量为颗粒直径、颗粒体积分数、颗粒速度及暂堵剂携带液黏度。模型裂缝宽度为6 mm，为保证计算过程颗粒占据流体单元空间，选择颗粒直径分别为1、2、3、4和5 mm，颗粒体积分数分别为4%、5%、6%、7%和8%，颗粒速度分别为0.5、1.0、1.5、2.0和2.5 m/s，暂堵剂携带液黏度分别为1、30、60、90和120 mPa·s进行模拟。同时，绘制粗糙裂缝模型，采用与光滑裂缝模型相同的尺寸、网格数、算例参数及监测数据，进行数值模拟及对比分析，揭示粗糙壁面对球形颗粒暂堵剂在裂缝内运移过程的影响。因变量为颗粒平均速度(速度)及颗粒受平均作用力。

4 数值模拟结果

颗粒直径、颗粒体积分数、颗粒速度和暂堵剂携带液黏度对暂堵剂缝内运移过程具有不同程度的影响[11-13],分别在光滑壁面和粗糙壁面的条件下对比影响因素的参数敏感性，分析暂堵剂颗粒在光滑裂缝和粗糙裂缝内的运移过程。

4.1 颗粒直径对暂堵剂缝内运移过程的影响

光滑裂缝和粗糙裂缝内暂堵剂颗粒直径对颗粒受力的影响见图6。由图6可以看出，随暂堵剂颗粒直径的增大，粗糙裂缝模型颗粒受平均作用力逐渐减小，与光滑裂缝模型的相同，但受力增量不同，相差近40.0倍。粗糙裂缝内暂堵剂颗粒之间相互作用力的影响处于次要地位，颗粒受力主要由颗粒在不同速度与粗糙壁面的阶梯部分碰撞产生。当颗粒直径较小时，颗粒数量较多，颗粒之间相互作用力较大，表现为暂堵剂颗粒受平均作用力大于光滑裂缝模型的。

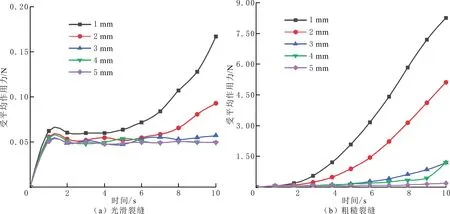
图6 两种模型颗粒受平均作用力随颗粒直径变化关系

光滑裂缝和粗糙裂缝内暂堵剂颗粒直径对颗粒速度的影响见图7。由图7可以看出，随暂堵剂颗粒直径的增大，粗糙裂缝模型颗粒速度逐渐减小，与光滑裂缝模型的相反；整体上，颗粒速度受颗粒直径影响显著，颗粒直径从1 mm增加到5 mm，颗粒速度降低55.6%；随颗粒直径的增加，相邻颗粒直径之间的颗粒速度差逐渐减小，当颗粒直径接近裂缝宽度时，对颗粒速度的影响基本保持不变。

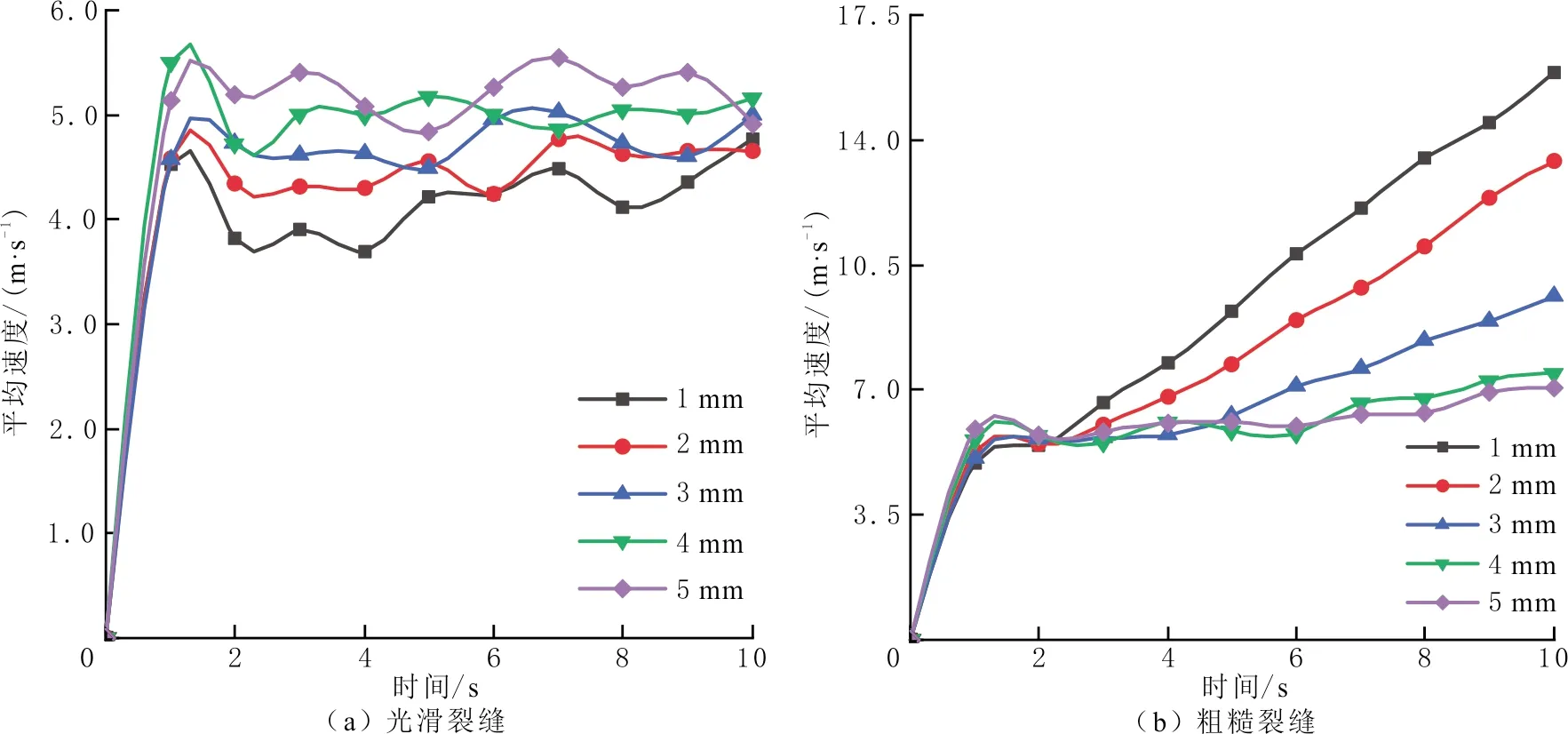
图7 两种模型颗粒速度随颗粒直径变化关系

4.2 颗粒体积分数对暂堵剂缝内运移过程的影响

光滑裂缝和粗糙裂缝内暂堵剂颗粒体积分数对颗粒受力的影响见图8。由图8可以看出，随暂堵剂颗粒体积分数的增大，粗糙裂缝模型颗粒受平均作用力逐渐增大，与光滑裂缝模型的相同，但受力增量不同，粗糙裂缝颗粒受平均作用力是光滑裂缝的25.8倍；粗糙裂缝内暂堵剂颗粒受平均作用力在注入时间4 s后产生较为明显的上升，在6 s后逐渐表现颗粒体积分数不同带来的影响，由于颗粒受平均作用力受裂缝表面粗糙度和颗粒之间相互作用力的共同影响，在计算区域的形状和大小不变时，颗粒体积分数过高导致颗粒数增加，影响颗粒活跃度，使每个单独颗粒活动空间减小，受力降低。

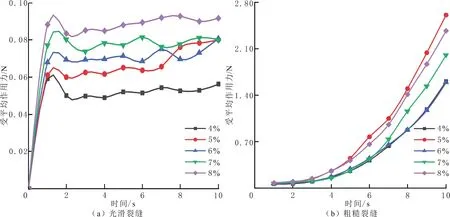
图8 两种模型颗粒受平均作用力随颗粒体积分数变化关系

光滑裂缝和粗糙裂缝内暂堵剂颗粒体积分数对颗粒速度的影响见图9。由图9可以看出，随暂堵剂颗粒体积分数逐渐增大，粗糙裂缝模型颗粒速度逐渐减小，与光滑裂缝模型的相反；当注入时间为0～5 s时，颗粒速度受颗粒体积分数影响不明显，注入时间6 s时，颗粒速度基本相同，注入时间6 s后，颗粒速度出现较大差距，颗粒体积分数为4%的颗粒速度比颗粒体积分数为8%的减小23.7%；与光滑裂缝模型的相反，粗糙裂缝模型颗粒体积分数对运移的影响显著，相邻颗粒体积分数之间颗粒速度的变化逐渐增大(见图9(b))。

图9 两种模型颗粒速度随颗粒体积分数变化关系

4.3 颗粒速度对暂堵剂缝内运移过程的影响

粗糙裂缝模型内垂直于y轴方向上裂缝剖面压力云图见图10。由图10可以看出，裂缝入口段为高压段，随颗粒速度逐渐增加，高压区域逐渐扩大，当流动区域逐渐被暂堵剂充满时，压力稳定在高压范围，压力波动区域逐渐被覆盖。

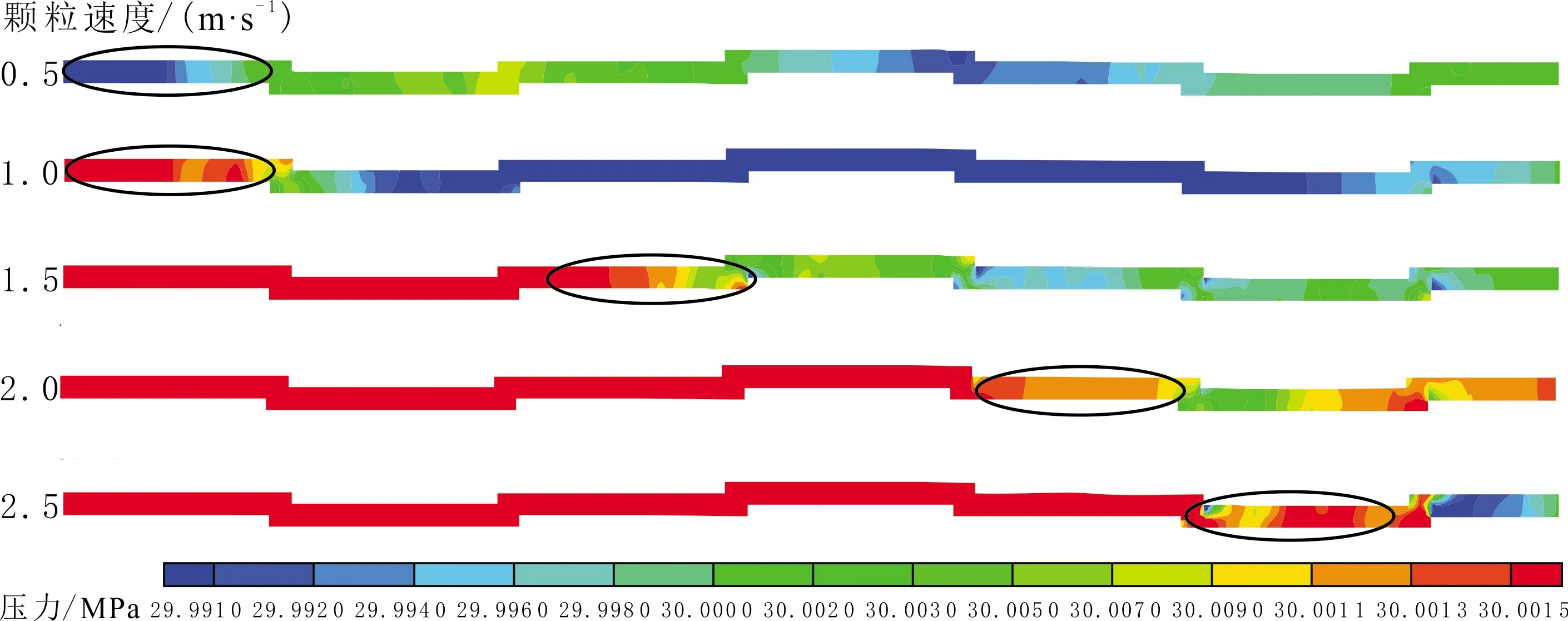
图10 粗糙裂缝模型剖面压力云图

光滑裂缝和粗糙裂缝内暂堵剂颗粒速度对颗粒受力的影响见图11。由图11可以看出，随暂堵剂颗粒速度的增大，粗糙裂缝模型颗粒受平均作用力逐渐增大，与光滑裂缝模型的相同，但受力增量不同，粗糙裂缝内颗粒受平均作用力是光滑裂缝的16.4倍；注入时间为4～10 s时，粗糙裂缝暂堵剂颗粒受平均作用力明显上升，注入时间为10 s时，颗粒受平均作用力是注入时间为4 s时的24.6倍，但颗粒速度为1.5 m/s的颗粒受平均作用力比颗粒速度为0.5 m/s时的增加8.1%；与光滑裂缝模型相反，颗粒受平均作用力对速度变量不敏感，裂缝粗糙表面是影响颗粒受力的主要因素。

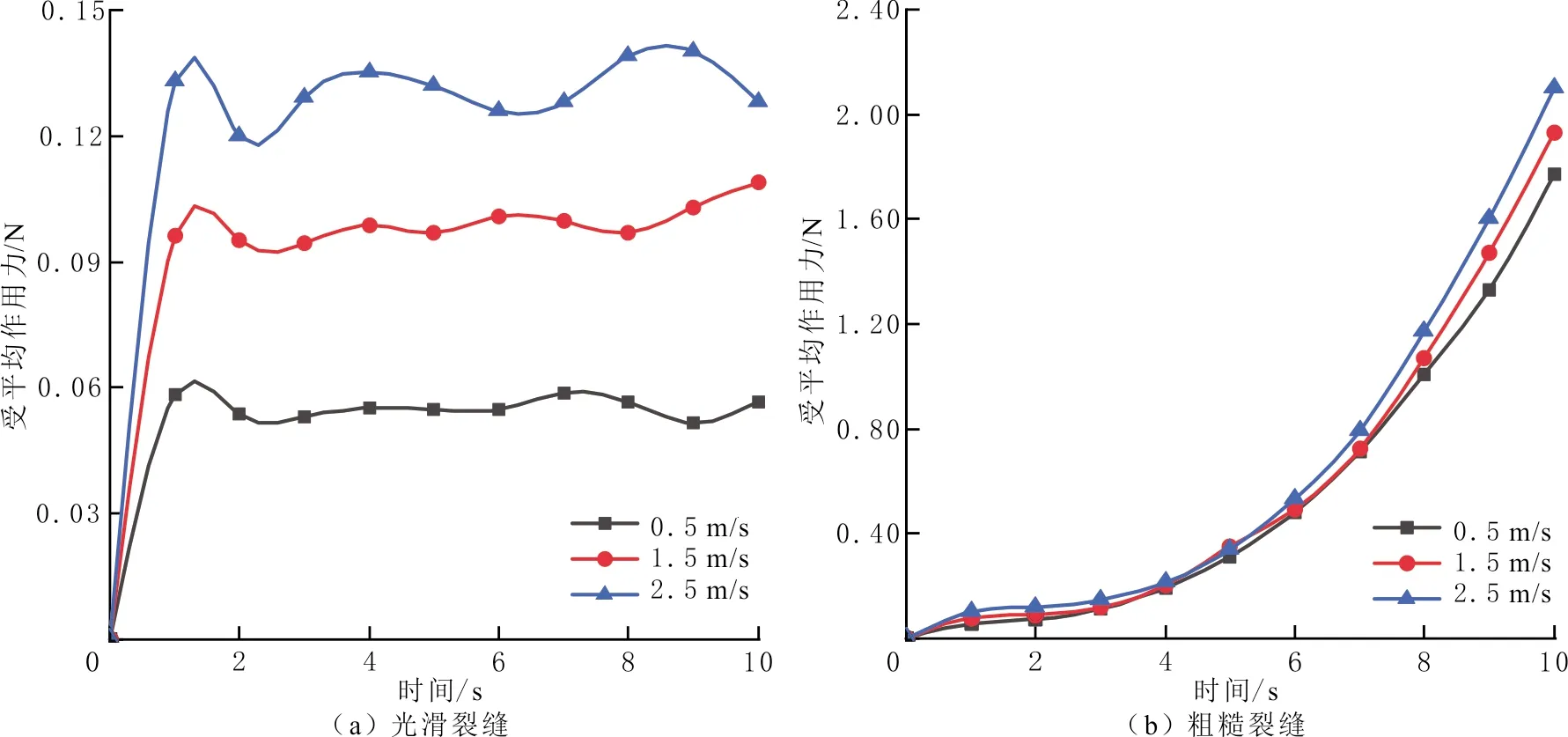
图11 两种模型颗粒受平均作用力随颗粒速度变化关系

4.4 暂堵剂携带液黏度对暂堵剂缝内运移过程的影响

光滑裂缝和粗糙裂缝内暂堵剂携带液黏度对颗粒受力的影响见图12。由图12可以看出，随暂堵剂携带液黏度的增大，粗糙裂缝模型颗粒受平均作用力逐渐增大，与光滑裂缝模型的相反，粗糙裂缝内颗粒受平均作用力是光滑裂缝的45倍；当注入时间为0～4 s时，颗粒受平均作用力增加不显著，当注入时间达到4 s时，受平均作用力迅速增加，当暂堵剂携带液流体黏度由60 mPa·s提升至120 mPa·s时，暂堵剂颗粒在缝内受平均作用力增加超过43.5%。高黏度流体对颗粒的运动产生阻碍作用，导致相同时刻停留在计算区域的颗粒数增加，提升颗粒之间相互碰撞的概率，碰撞力增加，总体受平均作用力随之增大。因此，流体的黏度越大，颗粒之间碰撞产生的平均作用力越强。

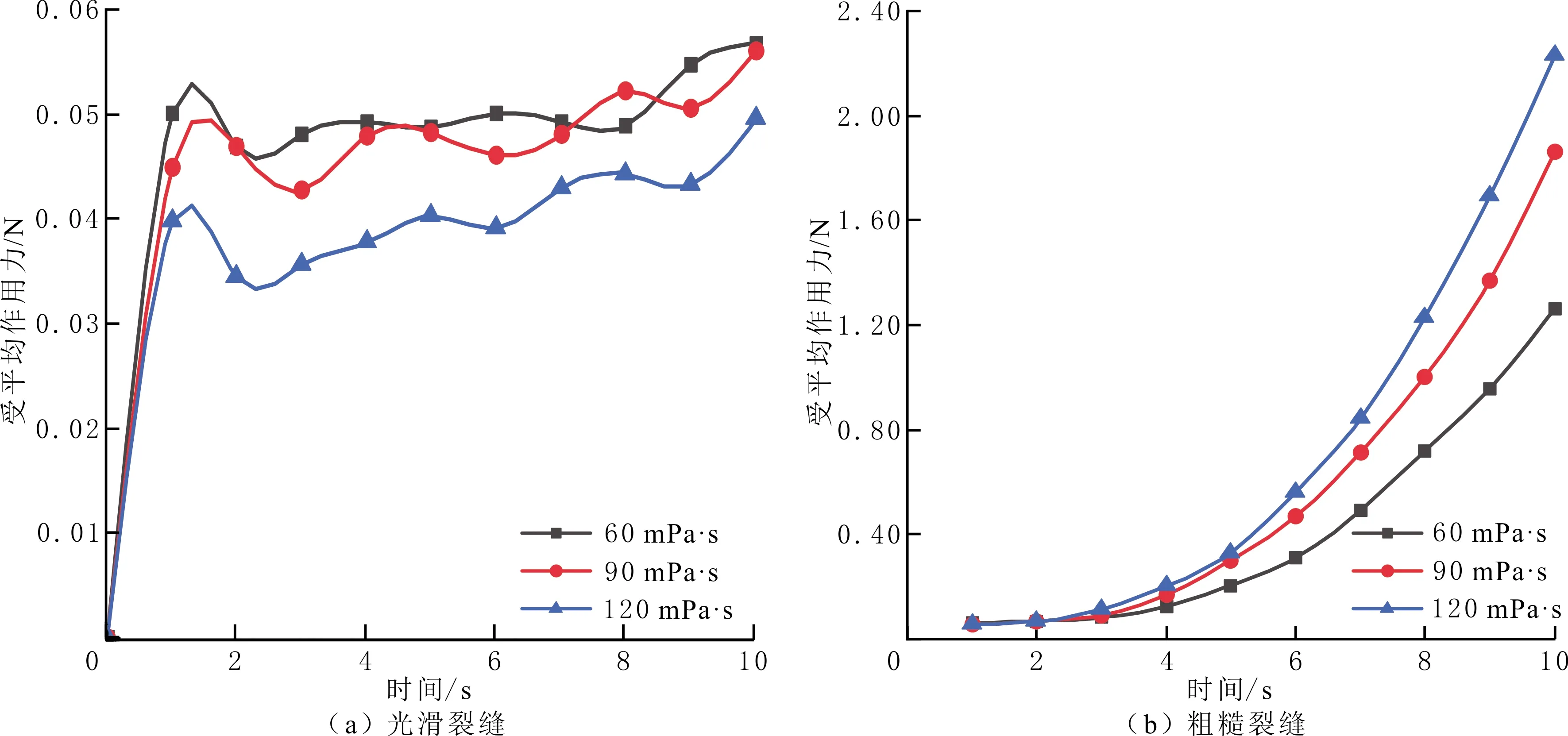
图12 两种模型颗粒受平均作用力随暂堵剂携带液黏度变化关系

光滑裂缝和粗糙裂缝内暂堵剂携带液黏度对颗粒速度的影响见图13。由图13可以看出，随暂堵剂携带液黏度的增大，粗糙裂缝模型颗粒速度逐渐增大，与光滑裂缝模型的相反；光滑裂缝模型暂堵剂经历进入裂缝初期颗粒速度迅速增加阶段后，颗粒速度逐渐稳定；粗糙裂缝模型由7个阶梯状的平行板模型组成，可以视为始终处于光滑裂缝初期，颗粒速度处于上升状态，粗糙裂缝内颗粒速度是光滑裂缝的2.4倍。

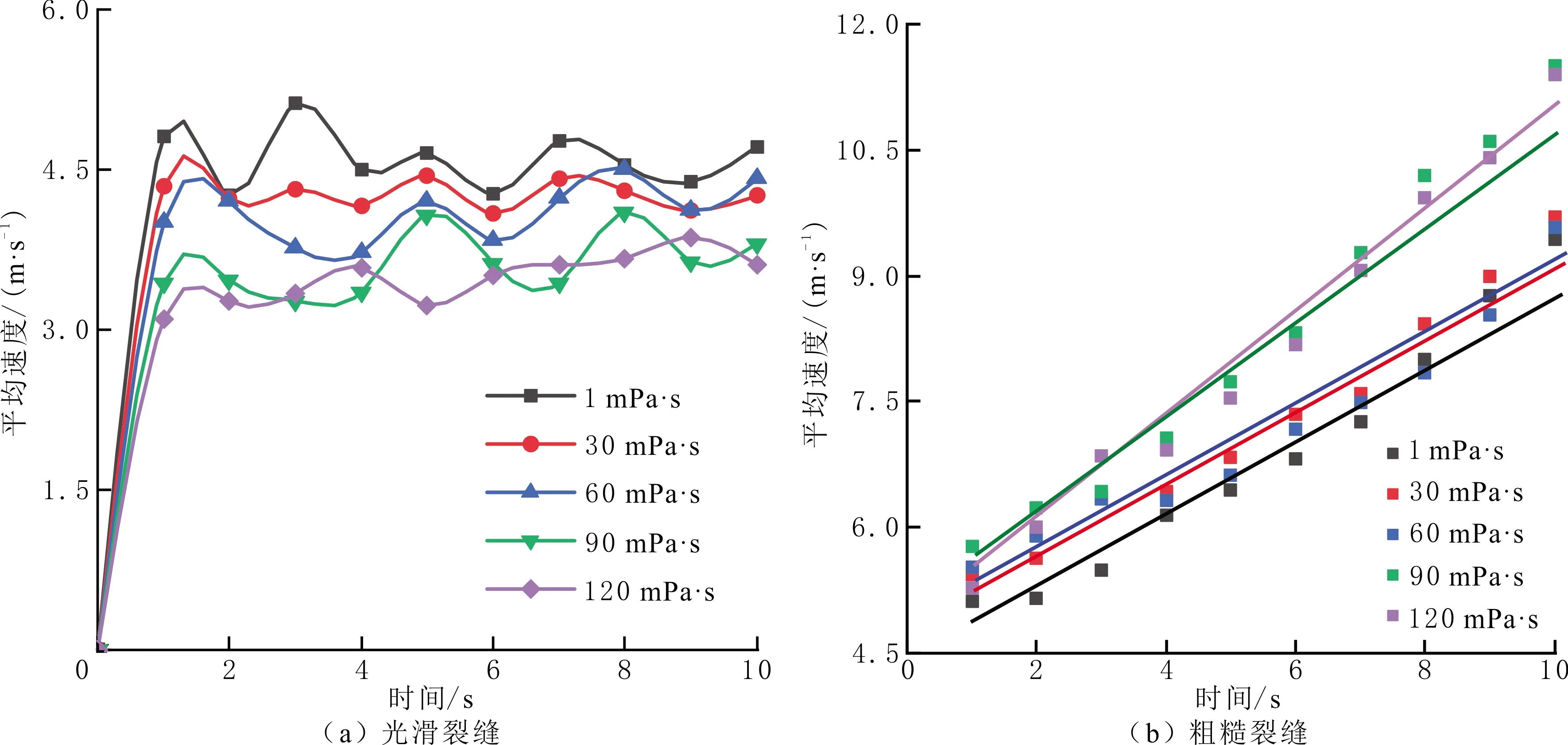
图13 两种模型颗粒速度随暂堵剂携带液黏度变化关系

不同暂堵剂携带液黏度粗糙裂缝剖面速度云图见图14。由图14可以看出，随暂堵剂携带液黏度的增加，缝内流体在近壁处的速度逐渐降低，携带液黏度越大，颗粒速度越低，从0.97 m/s逐渐降低到0.64 m/s。

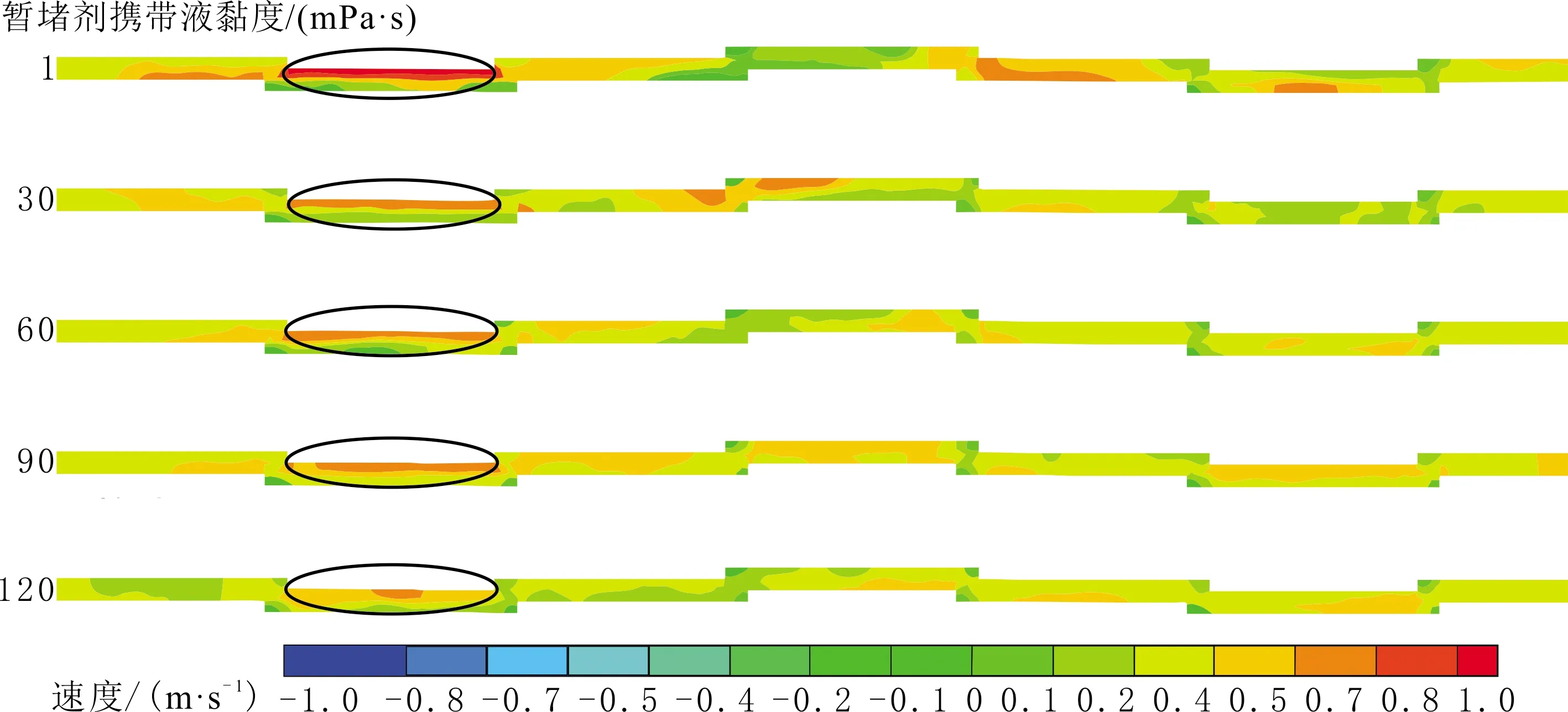
图14 粗糙裂缝剖面速度云图

暂堵剂携带液黏度从1 mPa·s增加到120 mPa·s时，流体形成湍流的能力逐渐减弱，湍流对暂堵剂运移的影响逐渐减小(见图15红色圈区域)；颗粒速度从50.19 m/s降低至25.29 m/s。

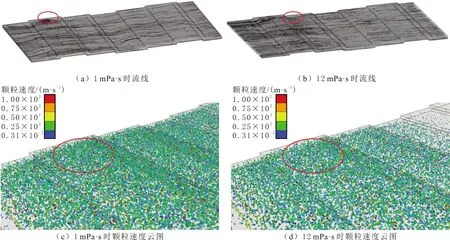
图15 注入时间0.5 s时不同黏度流动区域流线和颗粒速度云图

4.5 粗糙壁面与光滑壁面

不同裂缝粗糙特征对颗粒速度的影响见图16。由图16可以看出，当注入时间为0～2 s时，暂堵剂处于初始注入阶段，主要集中在裂缝入口附近，光滑裂缝与阶梯粗糙裂缝入口处几何特征相同，颗粒速度变化基本相同。随注入时间的增加，光滑裂缝内颗粒不受粗糙凸起的阻碍作用，颗粒运动规律不变，颗粒速度波动平稳。阶梯粗糙裂缝和真实粗糙裂缝颗粒与宏观粗糙凸起发生碰撞，导致颗粒混乱程度增加，颗粒速度随之增大。颗粒速度的变化规律整体表现为粗糙裂缝内颗粒速度大于光滑裂缝的，阶梯粗糙裂缝内颗粒速度为光滑裂缝的1.6倍，真实粗糙裂缝的颗粒速度约为光滑裂缝的1.3倍，阶梯粗糙裂缝与真实粗糙裂缝颗粒速度在整体变化趋势上相似，数值上相差21.0%，说明阶梯粗糙裂缝物理模型的正确性和必要性。

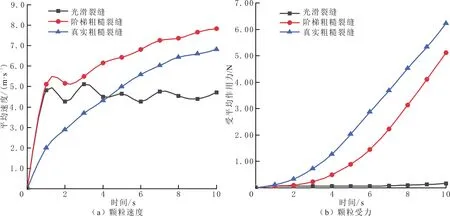
图16 两种模型颗粒速度及受平均作用力随裂缝粗糙特征变化关系

不同裂缝内的颗粒受平均作用力整体呈上升的趋势(见图16(b))。在初始注入阶段，3种不同裂缝颗粒受平均作用力变化不明显，当注入时间为0～1 s时，颗粒受平均作用力近乎重合。当注入时间为1～2 s时，光滑裂缝颗粒受平均作用力稳定在10-2数量级，阶梯粗糙裂缝颗粒受平均作用力略有提升，真实粗糙裂缝颗粒受平均作用力产生较大变化，说明光滑裂缝和阶梯粗糙裂缝颗粒主要受颗粒之间相互作用的影响，颗粒尚未与阶梯发生碰撞。对于真实粗糙裂缝，由于裂缝表面存在大量细小的粗糙凸起，与颗粒发生小规模的碰撞，导致颗粒受平均作用力大于其他裂缝的。当注入时间为2～10 s时，光滑裂缝颗粒受平均作用力始终保持稳定波动，阶梯粗糙裂缝与真实粗糙裂缝的宏观粗糙分布特征具有相似性，颗粒受平均作用力趋势也基本相同，阶梯粗糙裂缝与真实粗糙裂缝受平均作用力相差约为17.8%，光滑裂缝颗粒受平均作用力与阶梯粗糙裂缝和真实粗糙裂缝的相差30.7～37.2倍。

4.6 颗粒流态

通过对数值模拟结果的可视化处理得到不同时刻颗粒云图(见图17)。由图17可以看出，裂缝左侧为入口面，右侧为出口面。颗粒在裂缝内的运移过程可以分成3个阶段，分别为注入阶段、运移阶段和逃逸阶段。颗粒可以根据预设的形态规则泵入裂缝，注入阶段的颗粒相对比较密集；随注入颗粒数的增加，前期注入裂缝的颗粒逐渐向出口面运动，同时受颗粒和壁面、颗粒和颗粒、颗粒和流体的相互作用影响而逐渐分散，流态较为紊乱；当颗粒数继续增加时，后注入裂缝的颗粒推动先注入裂缝的颗粒向前运动，裂缝逐渐被颗粒填满，部分颗粒沿出口面逃出计算区域。

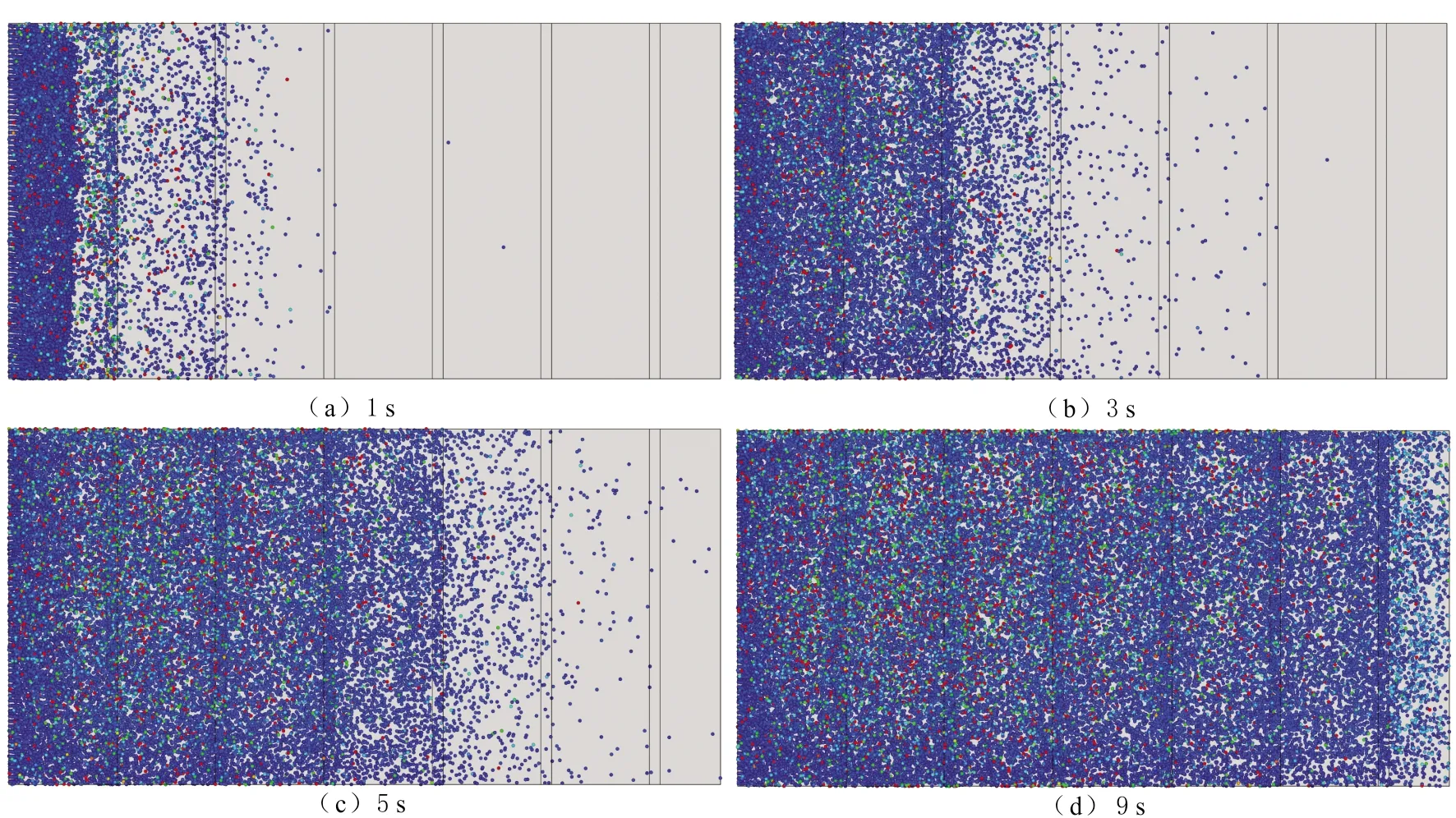
图17 不同注入时间粗糙裂缝模型颗粒运移过程

颗粒运移分为颗粒在光滑裂缝、阶梯粗糙裂缝和真实粗糙裂缝的注入阶段、运移阶段和逃逸阶段。当颗粒处于注入阶段时，颗粒在入口面附近产生一定程度的堆积，裂缝表面是否粗糙对颗粒运移没有显著影响(见图18)。

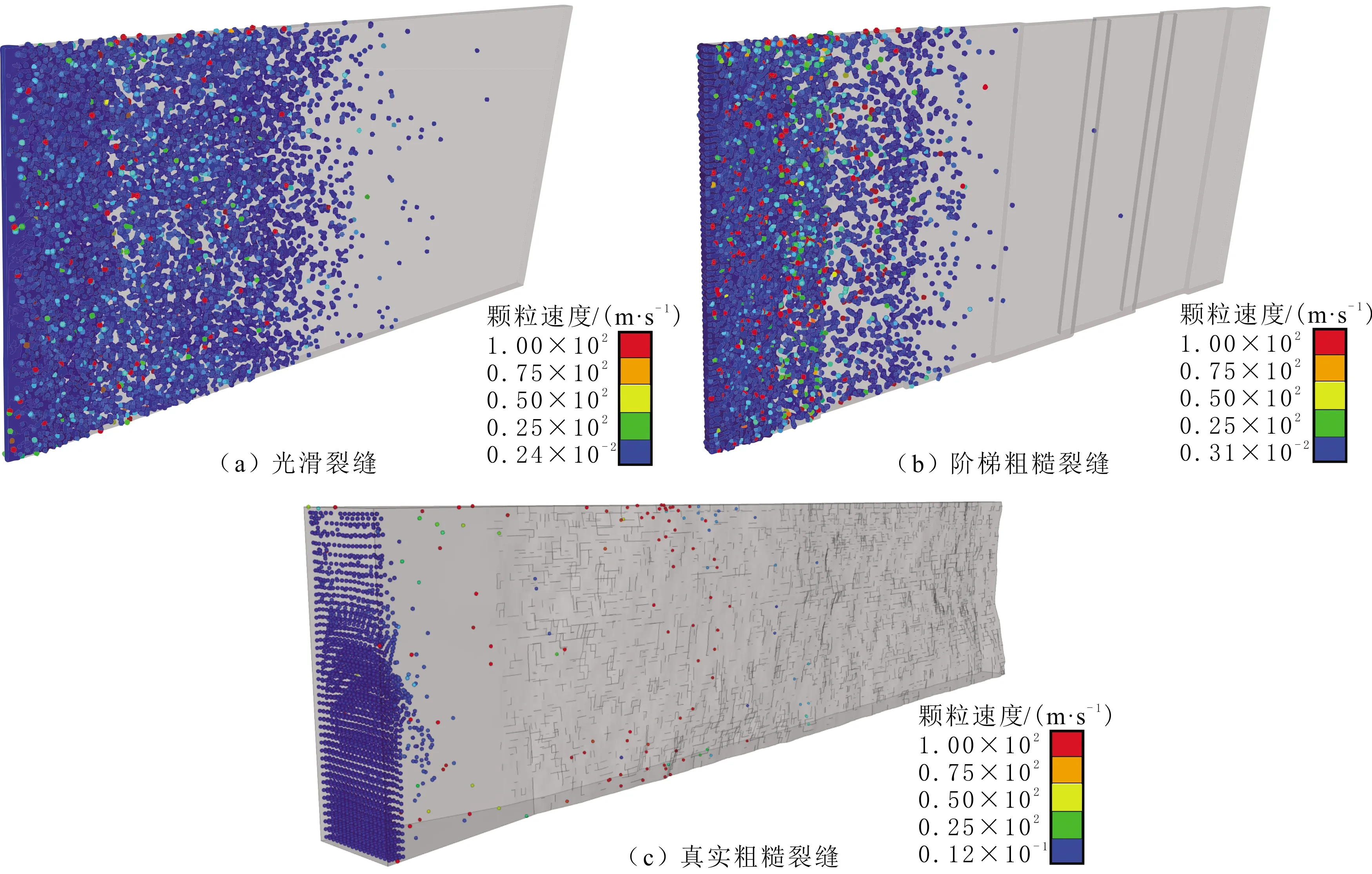
图18 光滑裂缝和粗糙裂缝模型颗粒注入阶段

当颗粒处于运移阶段时，裂缝粗糙表面对颗粒运移状态影响较大，光滑裂缝颗粒分散度差，大部分颗粒聚集在一起，同步向出口面方向移动；阶梯粗糙裂缝颗粒分散度优于光滑裂缝的，受阶梯粗糙凸起阻碍作用影响，颗粒与之发生碰撞，导致颗粒团被打散，颗粒混乱程度增加，随颗粒不断注入裂缝，混乱程度逐渐减小；真实粗糙裂缝颗粒分散度最优，真实裂缝不仅有宏观分布的粗糙特征，还有密集分布在裂缝表面的细小粗糙凸起，颗粒注入裂缝不断与之发生碰撞，不易产生颗粒聚集，颗粒始终处于较大的混乱状态(见图19)。

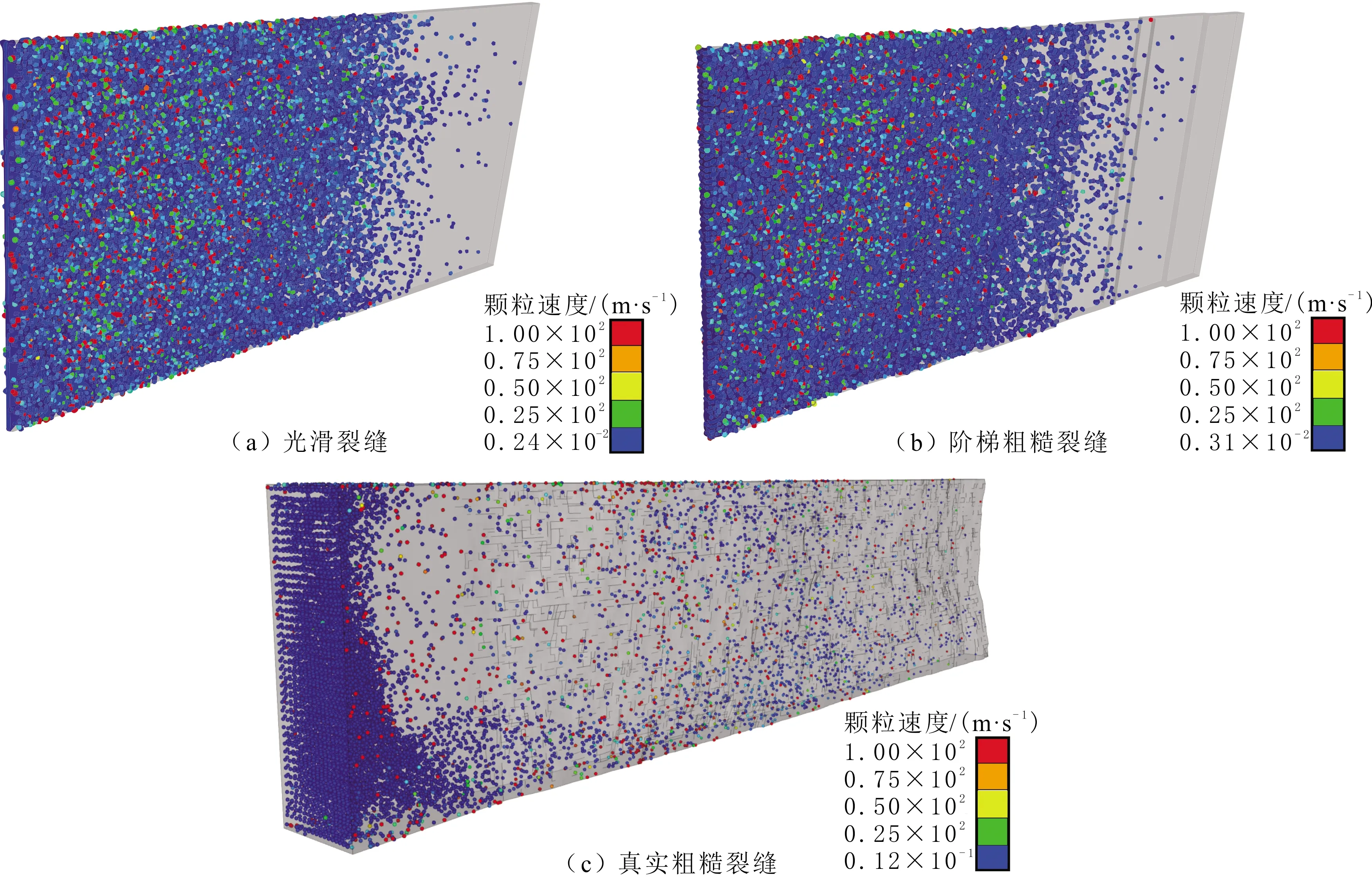
图19 光滑裂缝和粗糙裂缝模型颗粒运移阶段

当颗粒处于逃逸阶段时，光滑裂缝颗粒顺利通过裂缝，难以产生桥接；阶梯粗糙裂缝颗粒在靠近出口面的阶梯处产生一定程度的颗粒堆积，受物理模型的限制，堆积现象并不显著；真实粗糙裂缝表面大量细小粗糙凸起起到限制颗粒通过的作用，颗粒在凹陷位置停止运移，与壁面粗糙凸起产生桥接现象，进而导致小凸起逐渐演化为大凸起，产生较为明显的颗粒堆积现象(见图20)。

图20 光滑裂缝和粗糙裂缝模型颗粒逃逸阶段

4.7 讨论

粗糙裂缝颗粒受平均作用力受裂缝表面粗糙度和颗粒之间相互作用力共同影响，暂堵剂颗粒之间相互作用力的影响处于次要地位，颗粒受平均作用力主要由颗粒在不同速度与粗糙壁面的阶梯部分碰撞产生，当颗粒直径较小时，颗粒数较多，颗粒之间相互作用力较大。计算区域的形状和大小不变时，颗粒体积分数过高导致颗粒数增加，从而限制颗粒活跃度，导致每个单独颗粒活动空间减小，受平均作用力降低。与光滑模型颗粒受平均作用力情况相反，颗粒受平均作用力对速度变量不敏感，裂缝粗糙表面是影响颗粒受平均作用力的主要因素。同时，暂堵剂携带液黏度越大，颗粒之间碰撞产生的力越强，说明高黏度的流体对颗粒的运动产生阻碍作用，使相同时刻停留在计算区域颗粒数增加，从而间接增加颗粒体积分数，提升颗粒间相互碰撞的概率，碰撞力增加，总体受平均作用力随之增大。

支撑剂浓度、支撑剂颗粒直径和支撑剂携带液黏度等参数对支撑剂缝内运移及沉降过程产生影响[23-25]。当支撑剂颗粒体积分数较低时，颗粒仅在裂缝中心线附近流动，随颗粒直径与裂缝宽度比的增大，沉降速度下降得更快，当颗粒直径与裂缝平均宽度比为0.7～0.8时，沉降速度值为零。另外，壁面粗糙度和岩石非均质性等性质对颗粒沉降速度有显著影响，较大的表面粗糙度导致平均沉降速度快速降低[26-30]。裂缝储层的起裂、扩展和导流能力对支撑剂缝内运移过程产生较大影响[31-36]。

5 结论

(1)构建具有长度相等阶梯粗糙裂缝物理模型和CT扫描真实粗糙裂缝模型，分析参数敏感性，颗粒速度不是影响暂堵剂裂缝内运移过程的主要因素，而颗粒直径、颗粒体积分数和携带液黏度对球形颗粒暂堵剂在光滑裂缝和粗糙裂缝内运移过程有较大影响。

(2)改变颗粒直径可以在一定程度上控制颗粒在裂缝内的运移速度；颗粒体积分数过高导致颗粒受平均作用力降低；裂缝粗糙表面是影响颗粒受平均作用力的主要因素；高黏度的流体导致颗粒受平均作用力增大；粗糙裂缝内颗粒速度及受平均作用力高于光滑裂缝的。

(3)基于欧拉—拉格朗日方法的离散相数值模型可以用于模拟暂堵剂缝内运移过程，分析不同影响因素的作用规律，对暂堵转向压裂的经济性开发具有指导意义。