基于压裂液返排数据的页岩油气藏裂缝参数反演方法

张凤远，邹林君，崔 维，芮振华，李捷涵，潘 杨，张 伟，杨金智

(1.中国石油大学(北京)石油工程学院，北京 102249； 2.中国石油长庆油田分公司，陕西 西安 710018； 3.中国石油大学(北京)非常规油气科学技术研究院，北京 102249； 4.中海油研究总院有限责任公司，北京 100028； 5.The Pennsylvania State University, State College, USA 16801)

0 引言

中国常规油气藏普遍进入开发中后期，页岩油气藏勘探[1-2]和开发技术受到重视[3-4]，页岩油气藏开发进入快速发展时期[5]。水平井多段压裂是实现页岩油气经济开采的核心技术[6-9]，压裂效果评价和裂缝参数反演是页岩油气开发的重点和难点[10]。可以采用蕴含大量裂缝信息且十分经济的压裂液返排数据评价压裂效果，美国Eagle Ford和Marcellus等页岩油气藏证明压裂液返排数据在页岩油气开发中的重要作用。

人们建立多种非常规油气藏渗流数学模型并反演裂缝参数。ABBASI M等采用单相水模型分析返排数据、反演裂缝存储系数[11]。按照流体向裂缝窜流时间，CLARKSON C R等将致密油藏多段压裂水平井压裂液返排过程分为两个阶段，通过整合生产动态分析与历史拟合方法反演裂缝半长和导流能力[12]。为表征压裂液返排过程中的油水两相流动，CLARKSON C R等建立半解析返排模型，提出分析两相压裂液返排数据的流动物质平衡方法和典型曲线方法[12]。文献[13-14]将早期压裂液返排看作油水两相在封闭改造区域内的泄流过程，提出反演裂缝孔隙体积和渗透率的数学模型。KURTOGLU B等引入总流度和总产量概念，建立考虑油、气、水三相压裂液返排渗流模型[15]。这些模型与方法只考虑压裂液返排初期，忽略储层流体向裂缝窜流过程。

考虑压裂液返排后期油藏中的油气和滤失到储层中的压裂液向裂缝供给过程，CLARKSON C R等将试井分析中的动态动用区域(DDA)概念引入压裂液返排动态分析过程，建立致密储层半解析数学模型，同时考虑油水两相在裂缝和基质内的复合流动，对压裂液返排数据进行拟合，反演裂缝和储层参数[16]。CLARKSON C R等将压裂过程中的裂缝扩展模型与DDA模型相结合，对单孔介质[17]和双孔介质[18]油藏分别建立改进的压裂液返排数学模型，既可以分析压裂液返排数据，还能计算压裂液返排开始时裂缝和储层中的压力和饱和度分布，为压裂液返排模型的初始化提供重要依据。随体积压裂技术的推广，人们认识到两翼缝压裂液返排模型的局限性。CHEN Zhiming等[19]和JIA Pin 等[20]建立考虑复杂缝网的页岩油藏压裂液返排模型，实现油水两相在不规则裂缝网络内的流动模拟。ZHANG Fengyuan等对页岩气藏[21]和页岩油藏[22]提出反演裂缝参数的压裂液返排动态分析模型。这些压裂液返排后期渗流数学模型大多用在给定的储层和裂缝参数下进行正向模拟，不能反演裂缝参数，且缺少兼顾两相流动和页岩油气藏复杂渗流机理的系统性裂缝参数反演方法。

以不稳定渗流理论为基础，笔者建立一种适用于页岩油藏和气藏的压裂液返排渗流数学模型。该模型不仅考虑裂缝—基质间油水或气水两相复合流动，而且考虑两相流体在页岩储层内的复杂赋存和运移机理。引入拟压力、拟时间函数，结合物质平衡方程和Duhamel原理，对模型进行半解析求解，提出分析压裂液返排数据、反演裂缝初始孔隙体积和渗透率的直线分析法。

1 压裂液返排物理模型

为模拟多段压裂水平井压裂液返排过程，建立裂缝内两相流动与基质内两相流相耦合的渗流物理模型(见图1)。其中，km为基质渗透率；kf为压力相关裂缝渗透率；xf为裂缝半长；wf为缝宽；ym为半缝间距；Rom为有机孔半径；Rim为无机孔半径；δw,im为无机孔内近壁区域的水层厚度；vnw为无机孔内近壁区域水相的流动速度；vbh为无机孔内体相区域烃类流体流动速度；vsh为体相区域和近壁区域交界面处的烃类流体滑脱速度。压裂裂缝内充满压裂液(水相)及少量压裂过程中残留的油或气，返排过程中裂缝和基质内为气水或油水两相流动。在压裂液返排初期，压裂液为井的主要产出流体，大部分产出水来自裂缝，少部分产出水来自压裂过程中侵入到地层的压裂液。随返排进行，裂缝和基质之间压差增大，产出流体主要来源于基质内油或气向裂缝的窜流。

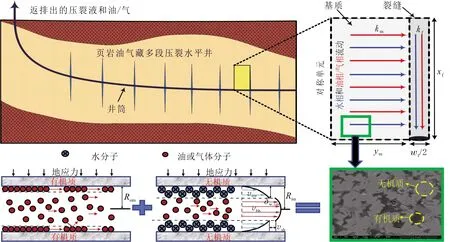
图1 页岩油气藏二维两相压裂液返排渗流物理模型

页岩储层具有源储一体的特点，储层孔隙结构、岩石物性、流体赋存方式及运移机理与常规油藏的有明显差别。为表征流体在页岩基质内的复杂渗流机理，根据扫描电镜图像[23]将基质系统分为带有纳米级孔隙的有机质和无机质。不同流体在不同类型孔隙内部具有独特的赋存和运移规律。

2 压裂液返排渗流数学模型

根据压裂液返排物理模型，裂缝—基质系统内流体的流动方式由近及远为：裂缝内压裂液和少量残余油或气向井筒流动、储层基质内流体受基质和裂缝之间压差作用通过裂缝面进行供给、基质内流体向垂直裂缝面方向流动。压裂液返排渗流模型可分为裂缝流动和基质流动，分别对两种流动过程进行建模，在裂缝面进行压力和流量耦合，建立压裂液返排不稳定流动渗流数学模型。

基本假设条件：

(1)储层均质等厚，流体在裂缝内流动遵循达西定律，忽略重力、毛细管力、井筒存储效应和表皮效应。

(2)各条裂缝的几何形态和裂缝参数相同，纵向穿透储层，忽略裂缝端面以外的流体供给。

(3)裂缝和基质微可压缩，油和水为微可压缩流体，具有恒定的压缩系数。气体满足真实气体状态方程。油、气、水的黏度和体积因数随压力变化。

(4)有机孔和无机孔为平行排列的圆形微纳米管，彼此之间没有流体传输。有机孔和无机孔具有相同的孔隙压力和应力敏感性。

(5)无机质具有亲水性，压裂液主要侵入基质的无机孔，无机孔内的水分子主要分布于近壁附近[24]。孔壁具有亲水性，可以忽略液—固界面处的滑脱效应。油或气赋存于无机孔的体相区域，油气分子与水膜之间具有滑脱效应。

(6)有机质具有疏水性，可以忽略储层改造过程中侵入到有机孔的压裂液，有机孔内为单相气或单相油。

(7)油相在有机孔内的赋存和流动状态遵循页岩油藏模型假设[25]，即在连续流基础上考虑滑脱效应和流体物性在孔壁区域和体相区域的不均匀分布特性。

(8)气相在有机孔内的赋存和流动状态遵循页岩气藏模型假设[21]，即在连续流基础上考虑滑脱效应、努森扩散、表面扩散和Langmuir单层吸附解吸规律。

2.1 裂缝流动

首先建立定产量生产条件下裂缝流动模型，然后利用Duhamel原理获得变产量生产条件下的模型解析解。基于页岩气藏[21]和页岩油藏[22]压裂液返排模型，建立适用于页岩油气藏的裂缝流动控制方程、初始条件和内外边界条件：

(1)

pf(x,0)=pfi,

(2)

(3)

式中：下角标j为w时表示水相方程，j为o时表示油相方程，j为g时表示气相方程；下角标i表示参数在初始条件下取值；x为沿裂缝方向的坐标；kf=kfiexp(-γf(pfi-pf))，γf为裂缝渗透率应力敏感模量；krj,f为裂缝中流体的相对渗透率；pf为裂缝压力；φf为压力相关的裂缝孔隙度，φf=φfiexp(-Cf(pfi-pf)),Cf为裂缝压缩系数；μj,f为裂缝内流体黏度；Bj,f为裂缝内流体体积因数；t为时间；qj为从裂缝流入井筒的流体流量；Cej,f为裂缝有效压缩系数，表达式为

(4)

式中：Sj,f为裂缝内流体饱和度；qsj为基质向裂缝的窜流量；Cj,f为裂缝内流体压缩系数；h为缝高。

裂缝流动控制方程通过式(4)耦合基质流动过程，将基质向裂缝的窜流等效为裂缝有效压缩系数的变化。式(1-3)中压力相关的裂缝和流体物性参数使控制方程具有很强的非线性，通过引入拟压力和拟时间函数(见表1)，可将裂缝流动控制方程线性化，利用分离变量法得到解析解：

表1 裂缝和基质的拟压力和拟时间定义

(5)

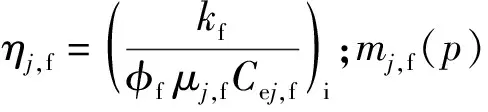
考虑式(5)的解析解过于复杂，无法直接用于参数反演，引入产量规整化拟压力RNPj=(mj,f(pfi)-mj,f(pwf))/qj，其中pwf为井底流压。利用文献[26]的方法对式(5)进行简化，得到定产量生产条件下的早期近似解和晚期近似解：

(6)

(7)

式中：Vfi为裂缝初始孔隙体积，Vfi=2xfwfhφfi；ε、α、β分别为单位转换因数，ε=1.932，α=1，β=0.977。

实际返排过程中，井通常以变产量的方式进行生产，定义两种形式的叠加拟时间tspj,1、tspj,2：

(8)

(9)

利用叠加原理，可以得到变产量生产条件下的早期近似解和晚期近似解：

(10)

(11)

2.2 基质流动

2.2.1 渗流基本模型

类似于裂缝流动控制方程，基质流动控制方程为

(12)

根据裂缝面压力连续性条件，将基质模型内边界处的压力设为平均裂缝压力，耦合裂缝流动和基质流动模型。初始条件和边界条件分别为

pm(y,0)=pmi,

(13)

(14)

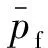
(15)

式中：Sj,m为基质内流体饱和度；Cj,m为基质内流体压缩系数；Cd为气体解吸附贡献的压缩系数，对于液体，Cd=0。

式(12-14)中与压力相关的基质和流体物性参数使得基质流动控制方程具有很强的非线性，引入拟压力和拟时间函数(见表1)，可将基质流动控制方程线性化。线性化的基质流动模型具有非齐次的内边界条件，即裂缝平均压力随时间变化。利用分离变量法和Duhamel原理[21]，得到基质方程的解析解为

(16)

(17)

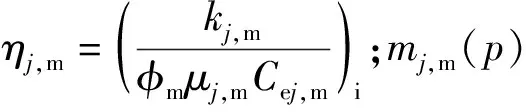
2.2.2 微观流动模型

2.2.2.1 有机孔单管

基于假设条件，有机孔壁具有疏水特性，孔内流体为单相气或单相油。结合页岩气藏微观流动模型[21]，气体在单根有机微纳米管内的总质量流量Jg,om表示为

(18)

式中：Kn,om为有机质的努森系数；Jsl,om为气体滑脱效应导致的质量流量；Jk,om为努森扩散导致的质量流量；Jsf,om为表面扩散导致的质量流量[21]。

若储层为页岩油藏，在连续流基础上，考虑应力敏感、滑脱效应和流体物性在孔壁区域和体相区域的不均匀分布特性等，结合页岩油藏微观流动模型[25]，油在单根有机微纳米管内的总质量流量Jo,om表示为

(19)

式中：Rom=Rom,iexp[0.5(Cm-γm)(pmi-pm)]；ρo,m和ρo,om分别为体相区域和近壁区域的油相密度；δo,om为有机孔内充满油相时的近壁区域厚度；μo,m和μo,om分别为体相区域和近壁区域的油相黏度；λo,om为油相在有机孔壁的滑脱长度。

为与渗流基本模型结合，利用达西定律将油相或气相的质量流量转化为页岩有机质的表观渗透率kh,om：

(20)

式中：φom为有机质孔隙度；τom为迂曲度。

2.2.2.2 无机孔单管

基于假设条件，无机孔内既包含烃类流体又包含水。由于无机孔壁具有亲水性，烃类流体占据体相区域，水相分布于近壁区域[27]。根据Hagen-Poiseulle方程，建立考虑滑脱效应的流动方程：

(21)

(22)

式(21-22)中：Rim=Rim,iexp[0.5(Cm-γm)(pmi-pm)]；μh,m和μw,im分别为体相区域烃类流体和近壁区域水相流体的黏度；δw,im为近壁区域的水层厚度；c1和c2为待定系数。

考虑烃类流体和水在体相区域和近壁区域交界面处的滑脱效应，同时忽略水在孔壁液—固界面上的滑脱效应，流动方程的内外边界条件为

(23)

vbh|r=Rim-δw,im=vnw|r=Rim-δw,im+vsh,

(24)

vnw|r=Rim=0。

(25)

当烃类流体为油时滑脱速度为vso，当烃类流体为气时滑脱速度为vsg，分别用油或气在固体界面上的滑脱速度[27]近似表示为

(26)

(27)

式(26-27)中：δv为切向动量调节因数，对于漫反射通常取为1；λg为气体平均自由程；λo为油在体相区域和近壁区域交界面处的滑移长度，λo=10-9×[0.387exp(-2×109Rim/32.47)+0.74]；vbg、vbo分别为无机孔内体相区域气体和油的流动速度。

将式(21-22)代入式(23-25)，可以得到无机孔内烃类流体和水在体相区域和近壁区域的流速剖面分别为

(28)

(29)

对体相区速度剖面从0到Rim-δw,im进行积分，对近壁区速度剖面从Rim-δw,im到Rim进行积分，可以得到烃类流体和水的体积流量，将质量流量表示为

(30)

(31)

式中：Jbh,im为烃类流体在无机孔内的质量流量；Jnw,im为水在无机孔内的质量流量；ρh,m和ρw,im分别为无机孔内体相区的烃类流体和近壁区域水的密度。

为与渗流基本模型结合，可以利用达西定律将油或气的质量流量转化为页岩无机质的表观渗透率kh,im：

(32)

式中：φim为无机质孔隙度；τim为无机质内孔隙的迂曲度。

基于有机孔和无机孔平行排列、无传质的假设，基质内烃类流体的综合表观渗透率为

kh,m=ψkh,om+(1-ψ)kh,im,

(33)

式中：ψ为基质内的有机质体积分数。

基质内水相只存在于无机孔，水相的综合表观渗透率为无机质内的水相表观渗透率：

(34)

式中表观渗透率计算过程中涉及到的近壁区域水层厚度δw,im与基质含水饱和度相关。

2.3 参数反演方法

2.3.1 平均压力和饱和度

基于文中的裂缝模型和基质模型，提出考虑页岩油气藏复杂渗流机理的裂缝参数反演方法——直线分析法：利用式(10-11)构建划分流动段的诊断曲线和求取裂缝参数的特征曲线，通过提取特征曲线上的斜率和截距计算裂缝初始孔隙体积和初始渗透率。在直线分析过程中，需要用到裂缝和基质的平均压力、饱和度等参数。

为计算拟压力和拟时间，需要计算裂缝和基质内平均压力、平均饱和度随时间的变化关系。分别对裂缝和基质建立物质平衡方程：

(35)

(36)

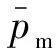
Vj,mi=yjxfhφmi,

(37)

(38)

式(37-38)中：yj为流体在基质内的调查距离。

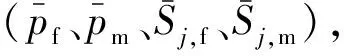
2.3.2 直线分析法

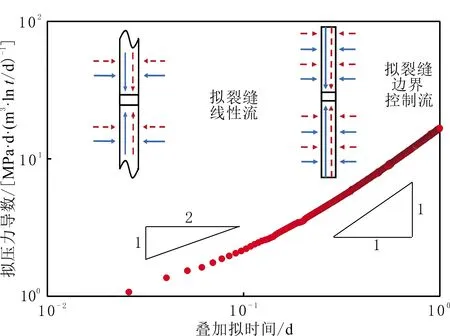
图2 二维两相流动诊断曲线

(39)

由式(11)可知，压裂液返排晚期RNPj和tspj,2呈线性关系，绘制在dRNPj/dlntspj与tspj的双对数曲线(诊断曲线)上呈斜率为1的直线(见图2[22])，与试井分析中的边界控制流类似[28]。由于这一阶段反映的是压裂液返排后期裂缝内的压力扰动传播到裂缝边界之后的流动状态，称为拟裂缝边界控制流。若已知裂缝的其他基本参数，则可以利用解释拟裂缝边界控制流阶段压裂液返排晚期数据的直线分析法，获得裂缝初始孔隙体积和渗透率，具体步骤：(1)将压裂液返排晚期数据绘制在诊断曲线上，提取斜率为1直线对应的数据时间段；(2)将返排数据以tspj,2为横坐标、RNPj为纵坐标绘制在直角坐标系上(拟裂缝边界控制流特征曲线)，提取特征曲线上对应步骤(1)中时间段的直线斜率(m2)和截距(b)；(3)计算裂缝初始孔隙体积Vfi,j和渗透率kfi,j,2：

(40)

(41)

为了进行直线分析，需要将Vfi作为输入参数代入物质平衡方程，求解平均压力和平均饱和度，绘制诊断曲线和特征曲线。Vfi作为待求解的变量之一，需要采用迭代求取裂缝参数：

(1)根据现场经验，给定一个裂缝初始孔隙体积Vfi作为迭代初始值。

(3)根据平均压力和平均饱和度，计算拟压力和拟时间(见表1)。

(4)绘制每一相流体对应的诊断曲线(见图2[22])，提取斜率为1/2和1的直线段对应的数据时间段。

(5)绘制拟裂缝线性流和拟裂缝边界控制流的特征曲线，对两个不同的流动段提取直线段的斜率和截距，代入式(39-41)求取Vfi和kfi。

(6)将解释的Vfi与迭代初始值进行对比。若相对误差大于设定公差，则将新求出的Vfi作为迭代初始值代入步骤(2)。若相对误差小于设定公差，则迭代收敛，输出计算的Vfi和kfi作为解释结果。

3 模型验证

利用裂缝和基质控制方程的解析解实现对裂缝参数的反演，由于平均压力和饱和度的计算过程涉及物质平衡方程的迭代求解，压裂液返排渗流模型为半解析模型，利用数值模拟对渗流模型进行验证。目前的数值模拟软件无法考虑基质内存在两相流条件下的微观渗流机理，无法对烃类流体和水相赋不同的表观渗透率函数。为验证渗流模型准确性，利用只考虑基质内烃类流体流动(假定基质内水相不流动)的数值模型对采取相应处理的半解析模型进行验证。

图3 直线分析辅助数据和曲线

基于式(10-11)，分别模拟水相和油相压裂液返排数据，绘制不同流动阶段下的直线分析法特征曲线(见图4)。提取直线段的斜率和截距，得到拟裂缝线性流阶段水相和油相数据解释的kfi,1分别为3.212、3.274 μm2，拟裂缝边界控制流阶段水相和油相数据解释的Vfi分别为15.404×103、15.546×103m3，水相数据解释的kfi,2为3.287 μm2。解释结果与模型的输入数据3.000 μm2和14.158×103m3相比误差不超过10%，满足工程上对参数反演的精度需求。拟裂缝边界控制流阶段油相数据解释的kfi,2为4.255 μm2，与输入数据误差较大，原因是基质窜流使得油相方程具有强非线性。参数反演过程中，以水相数据解释的kfi结果为准。

图4 早期和晚期流动阶段直线分析特征曲线

4 应用实例

以美国Marcellus页岩气藏一口多段压裂水平井为例，利用文中半解析模型和裂缝参数反演方法对该井的压裂液返排数据进行分析，评价压裂效果。该井分为22段压裂，每段5簇。压裂后进行24 d的返排，随后连续生产8个月。排采阶段的井底流压、产量历史及参数反演基本输入参数由ZHANG Fengyuan等[21]给出。ZHANG Fengyuan等[21,29]采用基质—裂缝两相复合流动模型和裂缝两相—基质单相模型，对该井压裂液返排数据进行分析，前者忽略流体在储层基质内的复杂运移和赋存机理；后者虽然考虑页岩气复杂渗流机理，但假设基质内为单相气体流动，忽略侵入储层中的压裂液对裂缝的供给过程。

首先给定一个Vfi作为迭代初始值，按照分析步骤求取新的Vfi对初始值进行更新。Vfi收敛后，得到裂缝平均压力和平均含水饱和度曲线(见图5(a))，以及基质内气相和水相向裂缝窜流量曲线(见图5(b))。初期产量以裂缝内流体为主，后期产量以基质供给为主。考虑复杂运移和赋存机理条件下气相和水相表观渗透率随压力的变化关系曲线(见图5(c))，气相表观渗透率随压力降低而逐渐升高，与基于单相气体假设得到的规律[21]一致。水相表观渗透率随压力降低而逐渐减小，与现场认识吻合，即压裂液返排后期侵入地层的压裂液越来越难产出。对于水相和气相返排数据，分别绘制不同流动阶段下的特征曲线(见图5(d-f))。由图5(d-f)可以看出，拟裂缝线性流阶段水相和气相数据计算的裂缝初始渗透率分别为1.027和1.079 μm2；拟裂缝边界控制流阶段水相和气相数据计算的裂缝初始渗透率分别为1.011和1.456 μm2，裂缝初始孔隙体积分别为4.69×103和5.31×103m3。不同相态、不同流动阶段数据解释的裂缝参数较为吻合且在合理的范围内，证明该方法现场应用的可靠性。

图5 文中模型Marcellus页岩气井现场应用结果

5 结论

(1)建立一种普遍适用于多段压裂水平井油藏和气藏的压裂液返排半解析渗流数学模型，不仅考虑裂缝—基质间油水或气水两相复合流动，而且考虑两相流体在页岩储层内的复杂渗流机理。

(2)提出一种划分两相流动阶段的诊断曲线和反演裂缝参数的直线分析法，能够对裂缝初始孔隙体积和裂缝初始渗透率进行准确反演。压裂液返排过程可分为拟裂缝线性流和拟裂缝边界控制流，在诊断曲线上分别呈斜率为和1的直线。

(3)受流体在储层中的复杂渗流机理影响，气相和水相表观渗透率随压力降低呈不同的变化趋势。受现场数据测量精度影响，拟裂缝边界控制流的直线段持续时间更长且更明显，该阶段的数据更适宜进行裂缝参数反演。