考虑非达西效应的边水气藏水平井见水时间预测模型

石军太，张龙龙，羊新州，洪舒娜，李星浩，李文斌，鲁家国

(1.中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249； 2.中国石油大学(北京)煤层气研究中心，北京 102249； 3.中海石油(中国)有限公司 深圳分公司，广东 深圳 518067)

0 引言

边水气藏开发过程中容易发生水体侵入，气井见水后气体流速过低不能将液体携带出去，导致气井不断积液而形成恶性循环，直至气井发生水淹，造成气井产能和气藏采收率下降，影响气藏的开发效果[1-6]。准确预测气井的见水时间对于气藏开发方案的制定具有重要作用。目前，预测水驱气藏见水时间的方法通常有三种：第一种为数值模拟方法，参数多且操作复杂，不便于现场实际操作；第二种为体积平衡的方法，需要的水体参数如形状、孔隙度等在实际中难以准确获取，误差较大；第三种为基于多孔介质流体质点渗流理论的方法。

结合理论分析与实践验证，人们对气藏见水时间开展研究。对于底水气藏见水时间预测，有较丰富的研究成果[7-11]。基于多孔介质流体质点渗流理论，ZHU Weiyao等[12]考虑气水流度比、束缚水饱和度、残余气饱和度等因素，对底水均质气藏水平井见水时间进行研究，并推导见水时间计算公式。黄全华等[13]应用半球形渗流模型，考虑气相非达西效应，计算带隔板的底水气藏见水时间。胡平等[14]利用镜像反映及势的叠加原理，建立带隔板的底水油藏水脊模型，见水时间误差较小。基于渗流理论，明瑞卿等[15]考虑多种因素的影响，建立凝析气藏见水时间预测模型，在实际应用中具有指导意义。对于边水气藏水平井见水时间的预测，主要考虑高速非达西效应、储层倾角[16]及水平井长度等因素的影响。吴克柳等[17]考虑反凝析因素与近似直线供给边界，建立边水凝析气藏的见水时间预测模型。根据物质平衡理论，李志军等[18]建立圆环形边水气藏的见水时间预测模型。基于多孔介质流体质点渗流理论和硫沉淀模型，GUO Xiao等[19]考虑束缚水饱和度、残余气饱和度、气井与边水距离、气相非达西效应等因素，建立边水高硫气藏见水时间预测模型，并验证模型的有效性。基于气液两相流渗流理论，明瑞卿等[20]考虑储层倾角、水平井长度的影响，建立倾斜地层水平井边水气藏见水时间预测模型；同时考虑气相非达西效应与反凝析因素，推导边水气藏的见水时间计算公式[21]。基于多孔介质流体质点渗流理论，黄全华等[3]考虑水平井长度、高速非达西效应及近似直线供给边界，应用椭球形水平井渗流模型，预测边水气藏水平井的见水时间。基于椭球形水平井渗流模型，HUANG Quanhua等[22]将边水推进分为两个过程，建立边水凝析气藏见水时间预测模型。

已有的见水时间预测模型考虑的影响因素较单一，仅研究水质点的舌进过程。当储层倾角与气水边界较大而气井产量较小时，基于气液运动方程，气水边界的水质点驱动力可能小于重力分量，水质点将没有舌进速度，已有的见水时间预测模型不再适用。对于气井见水时间的计算，既要考虑水质点舌进，又要考虑水侵速度的影响。笔者考虑水侵速度、气相非达西效应、储层倾角、水平井长度等因素的影响，建立边水气藏水平井见水时间预测模型，以P边水气藏W井为例，验证模型的合理性，并对影响因素进行敏感性分析。

1 模型建立

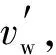
假设边水气藏的气水边界附近有一口水平井，气水边界为直线，边水距离为a，水平井长度为L，储层倾角为θ，水驱最前缘点与水平井距离为r，储层厚度为h。根据渗流力学理论，水平井渗流物理模型为椭球形[23]，边水气藏水质点舌进示意见图1。水舌的最前缘点M最先到达水平井的中点N，气井开始见水，水质点M的舌进速度最大。

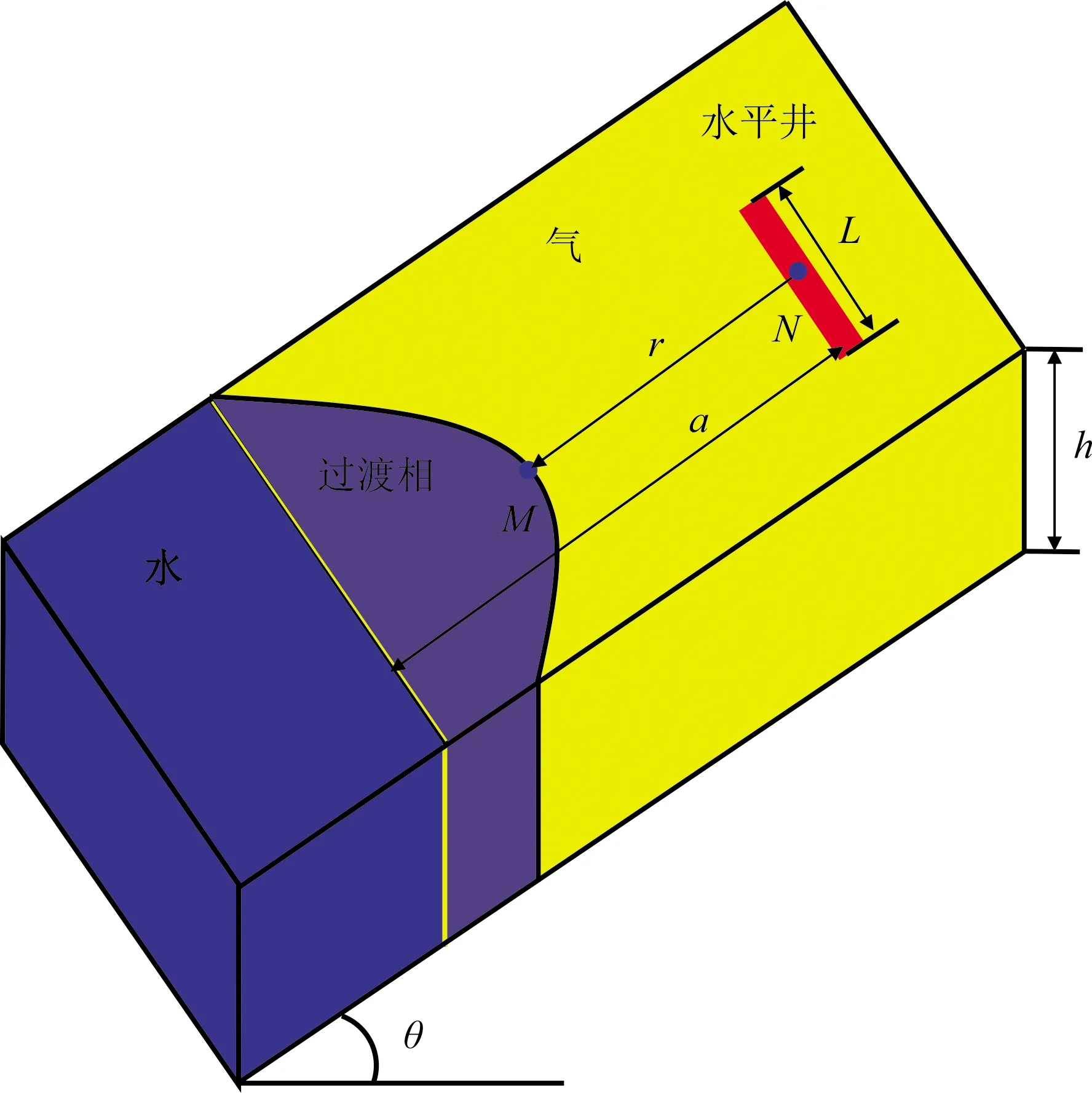
图1 边水气藏水质点舌进示意

1.1 舌进速度

模型假设条件：(1)整个储层均质等厚，水运移过程为活塞式水驱气过程；(2)忽略毛管力的影响；(3)水相满足达西定律，气相满足非达西渗流定律；(4)气水黏度与密度保持不变。

根据气水两相渗流规律，考虑重力的影响及气相非达西效应的气、水运动方程[24]，气相、水相压力pg和pw的微分方程分别为

(1)

(2)

式(1-2)中：vg为气相渗流速度；Kg和Kw分别为气相和水相渗透率；μg和μw分别为气相和水相黏度；ρg和ρw分别为气相和水相密度；g为重力加速度；β为描述孔隙介质紊流影响的系数[25-26]。

忽略毛管力的影响，则有

(3)

联立式(1-3)，并将各物理量的单位转换为矿场单位，水相渗流速度只有舌进速度，即

(4)

(5)

(6)

式中：Mrgw为气水流度比；Krg为气相相对渗透率；Krw为水相相对渗透率。

令

(7)

(8)

则式(4)变形为

(9)

假设水平井的等势面为近似椭圆环面(见图2)，气水界面的最前缘点M在环面上，则气体渗流速度[23,27]为

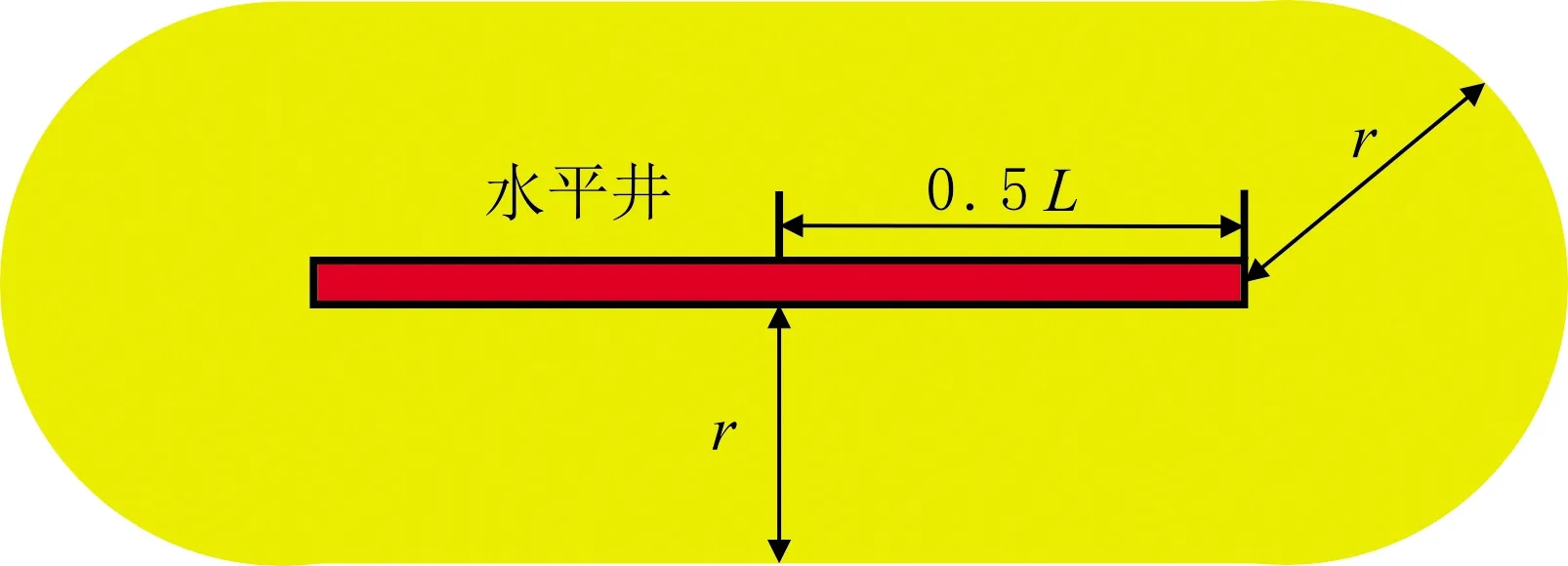
图2 水平井近似椭圆等势面

(10)

式中：qg为气井产量；Bg为气体体积因数。

(11)

当驱动力小于重力分量时，水质点没有舌进速度，即vw=0 m/s时，M点所在边界为临界边界，记为rc，化简得到临界边界的表达式为

(12)

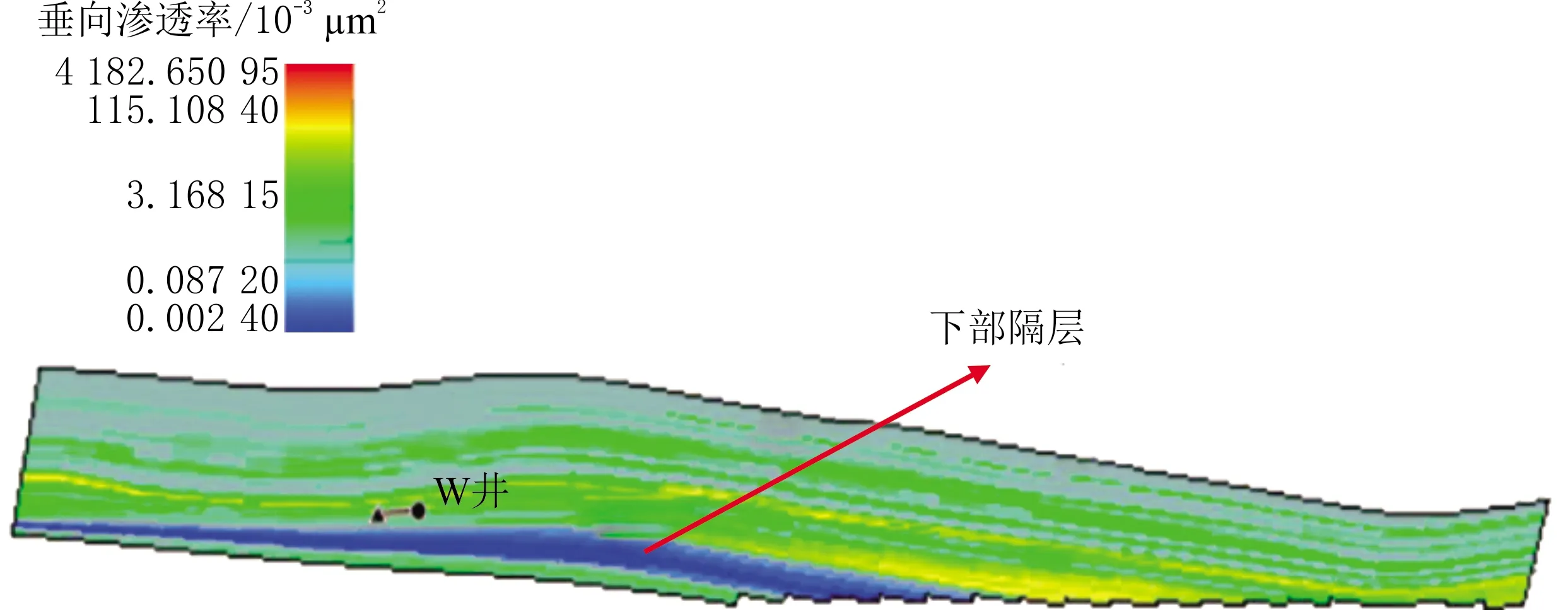
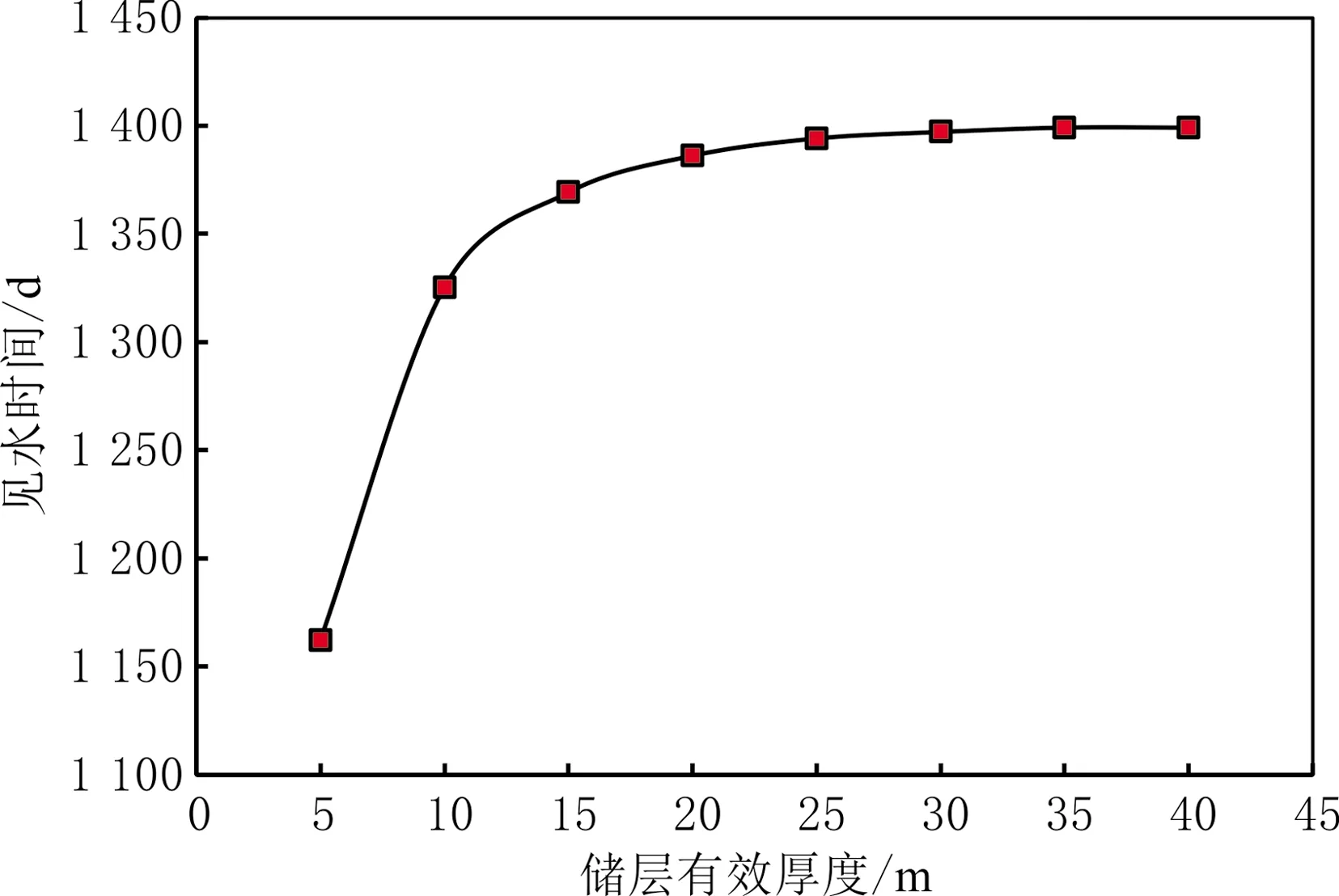
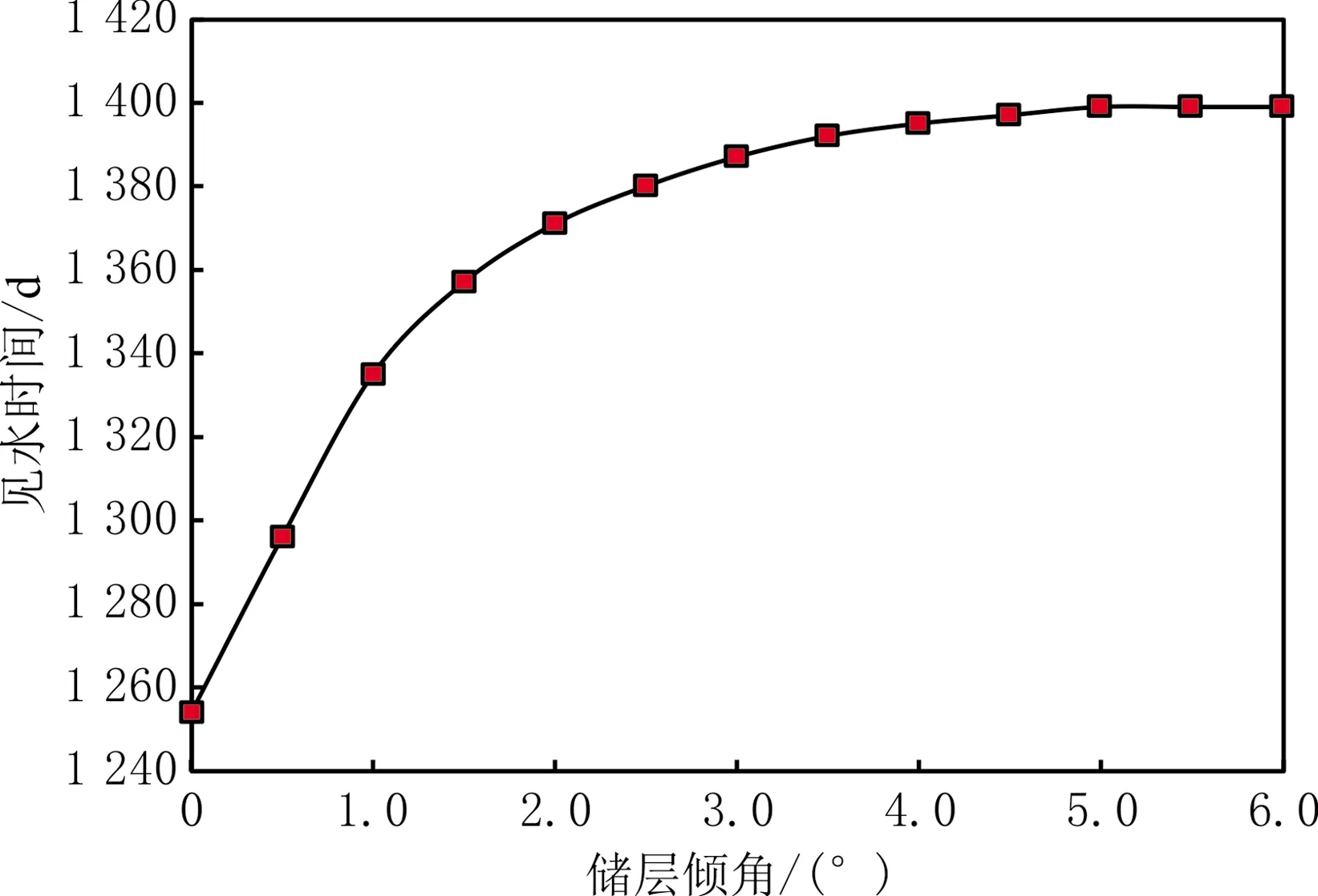
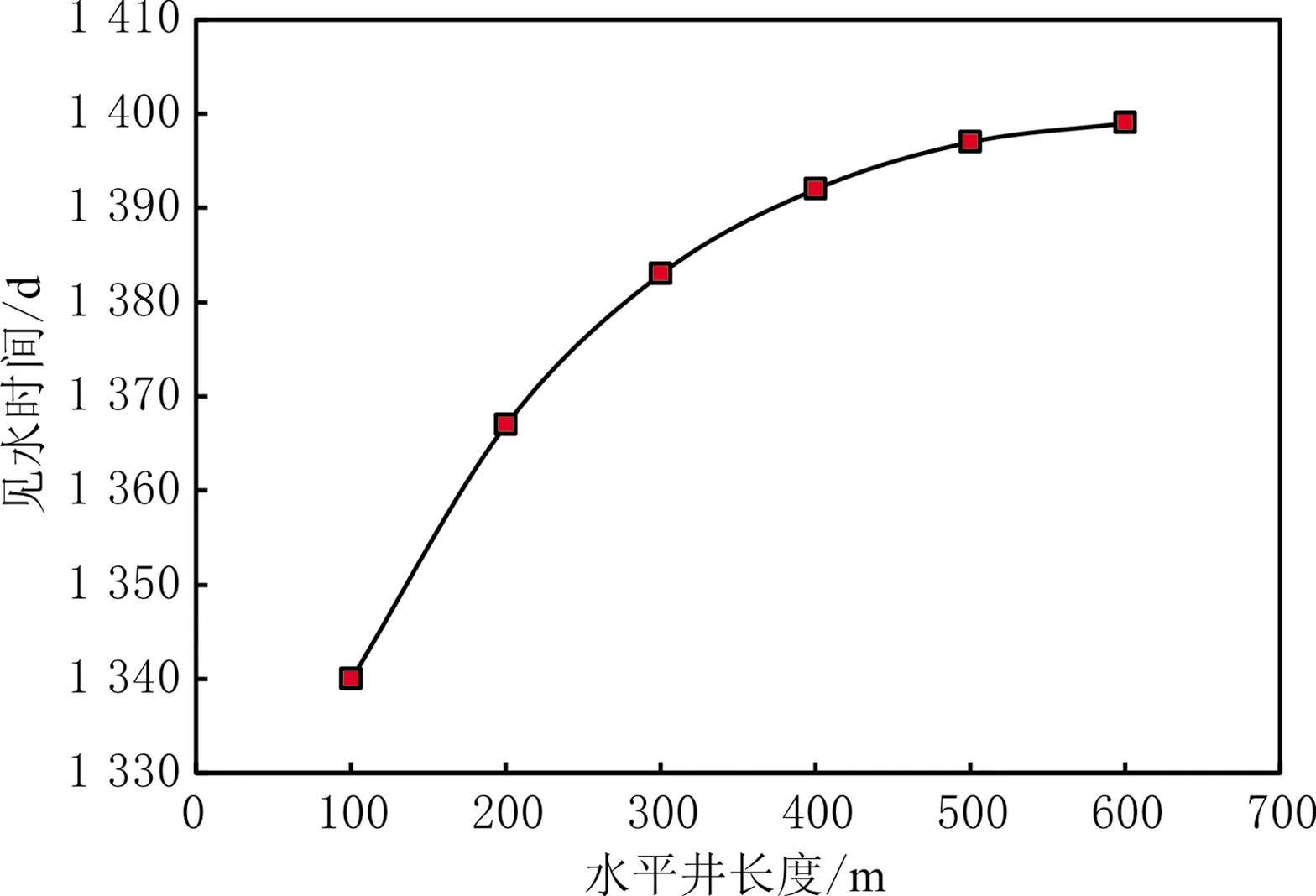
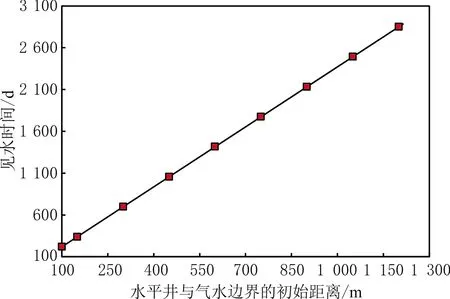
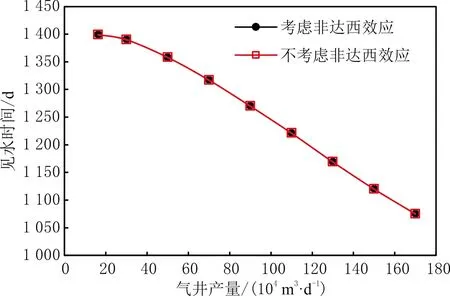
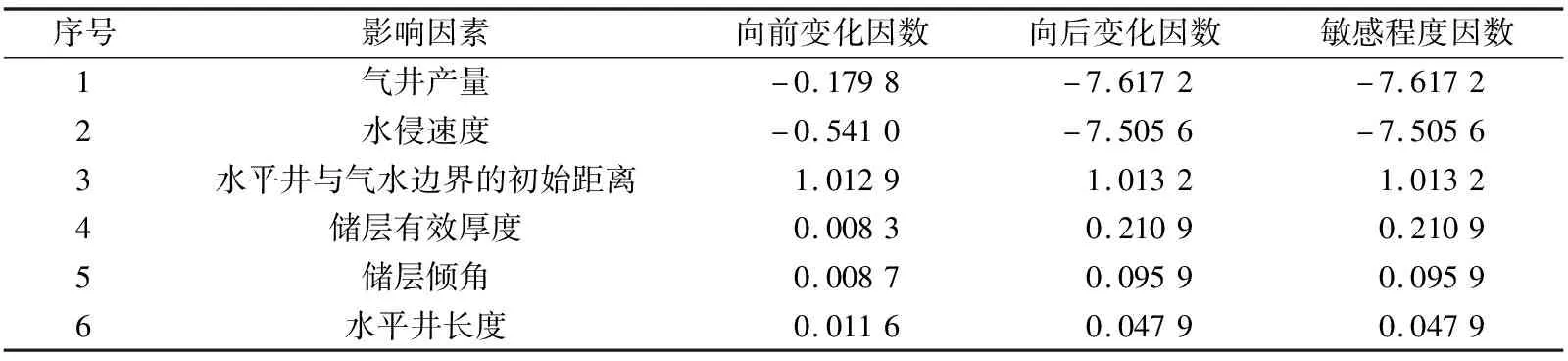
整个水质点的运移过程可以分为两个阶段：当r≥rc时，水质点只有水侵速度；当r

1.2 水侵速度

随气藏的开采，边水逐渐侵入储层，关于水侵量计算模型的研究较充分，其中包括Schilthuis稳态模型、Van Everdingen-Hurst非稳态模型、Carter-Tracy非稳态模型、Fetkovich拟稳态模型[28]及物质平衡模型[29]。采用物质平衡模型计算水侵量，即

(13)

式中：Gp为累计产气量；n′为等效水体倍数；G为原始地质储量；Bgi为原始条件下天然气体积因数；Swi为原始含水饱和度；Cw为水的等温压缩系数；Cp为孔隙压缩系数；b为水体波及体积修正因子。当b=0时，水体波及速度极快，不考虑水体波及动态过程；当b=1时，水体波及体积与累计产气量呈正相关关系。

假设水侵过程是一个稳定的过程，根据水侵量、储层有效厚度及气水边界长度，计算水侵速度为

(14)

式中：ΔWe为时间间隔Δt的水侵量之差；c为气水边界长度。

1.3 见水时间

在多孔介质中，水质点真实渗流速度表达式为

(15)

式中：v为达西渗流速度；φ为孔隙度。

考虑残余气及束缚水的影响，式(15)可写作

(16)

式中：Sgr为残余气饱和度。

考虑非达西效应、水侵速度及储层倾角的影响，根据气水边界与水平井的距离a与rc的关系，可分两种情况计算气井见水时间：

(1)a≥rc。水质点向井底运移的过程分为两个阶段：第一阶段为从气水界面到临界边界，水质点只有水侵速度；第二阶段为从临界边界到水平井的中心点，水质点既有水侵速度，又有舌进速度。式(16)可变形为

(17)

式中：tbt为见水时间。

根据式(17)积分可得气井见水时间为

(18)

(19)

(20)

式中：Krgwi为束缚水影响下的气相相对渗透率；Krwgr为残余气影响下的水相相对渗透率。

(2)a

(21)

根据式(21)积分可得气井见水时间为

(22)

对式(18)和式(22)积分求出的解析解表达式较复杂，可以用数值方法计算满足精度的数值解。

当不考虑气相非达西效应、仅考虑水侵速度及倾角的影响时，A=0，代入式(11)求得临界边界rc为

(23)

当a≥rc时，可推导气井见水时间为

(24)

当a

(25)

当地层水平且不考虑非达西效应时，A=0，B=0，由于没有重力的影响，不存在临界边界，整个水质点运移过程中同时存在水侵速度与舌进速度，气井见水时间为

(26)

当不考虑水侵速度、储层倾角及气相非达西效应时，整个水质点运移过程只有水质点的舌进过程，气井见水时间为

(27)

2 模型验证

P边水气藏W井于2010年1月投产、2014年6月见水，实际见水时间约为1 478 d(见图3)，气井储层基本物性参数见表1，储层的隔层分布及附近水体分布见图4。

图3 W井水气比分布

表1 W井储层基本物性参数

图4 W井储层的隔层分布及附近水体分布

W井主要受南部边底水影响，由于垂向渗透率较低且射孔段下部存在明显隔层，主要为边水侵入。采用考虑水侵速度、气相非达西效应及储层倾角的见水时间预测模型，计算满足精度的数值解，利用Python数值积分库Scipy进行求解，W井见水时间为1 391 d，与实际见水时间较接近，相对误差为-5.9%。当不考虑水侵速度、储层倾角及气相非达西效应的影响时，即仅考虑水质点舌进过程，见水时间为37 854 d。因此，气井见水时间计算必须综合考虑水质点的舌进过程与水侵过程，建立的见水时间预测模型可靠性高，可以有效指导边水气藏的合理高效开采。

3 敏感性分析

以W井的相关物性参数为基础数据，采用见水时间预测模型对储层有效厚度、储层倾角、水平井长度、水平井与气水边界的初始距离、水侵速度、气井产量及气相非达西效应等影响因素进行敏感性分析。

3.1 储层有效厚度

储层有效厚度对见水时间的影响见图5。由图5可知，见水时间随储层有效厚度的增大而增大，当储层有效厚度较小时，见水时间变化很大；当有效厚度增大到一定值后，见水时间的增大程度逐渐减缓。这是由于随储层有效厚度增大，气体渗流速度逐渐减小，使水质点舌进速度减小，同时临界边界减小，水质点舌进距离减小，导致见水时间增大。当储层有效厚度继续增大、临界边界减小到0 m时，水质点运移过程只有水侵过程，没有舌进过程，只受水侵速度的影响，见水时间保持不变。

图5 W井储层有效厚度对见水时间的影响

3.2 储层倾角

储层倾角对见水时间的影响见图6。由图6可知，见水时间随储层倾角的增大而增大，当储层倾角较小时，见水时间变化较大；当倾角增大到一定值后，见水时间保持不变。这是由于初始增大储层倾角，水质点舌进速度减小，临界边界减小，舌进距离也减小，导致见水时间增大。当储层倾角增大到一定值后，驱动力小于重力分量，水质点没有舌进速度，只受水侵速度的影响，见水时间保持不变。

图6 W井储层倾角对见水时间的影响

3.3 水平井长度

水平井长度对见水时间的影响见图7。由图7可知，随水平井长度的增加，见水时间逐渐增大，但增长程度逐渐减小。这是由于随水平井长度增加，泄气区逐渐增大，气体渗流速度逐渐减小，使水质点舌进速度减小，临界边界减小，导致水质点的舌进距离减小，见水时间增大。当水平井长度继续增加、临界边界减小到0 m时，整个水质点运移过程只有水侵过程，见水时间保持不变。

图7 W井水平井长度对见水时间的影响

3.4 水平井与气水边界的初始距离

水平井与气水边界的初始距离对见水时间的影响见图8。由图8可知，见水时间随初始距离增大而增大的趋势明显，近似直线关系。这是由于气水边界与水平井间的初始距离增大，水质点运移的路程增大，见水时间增大。

图8 W井水平井与气水边界的初始距离对见水时间的影响

3.5 水侵速度

水侵速度对见水时间的影响见图9。由图9可知，见水时间随水侵速度的增大而减小，当水侵速度较小时，对见水时间的影响更敏感；当水侵速度增大到一定值后，见水时间减小程度变小。这是由于初始增大水侵速度时，水侵速度与舌进速度相当，见水时间迅速减小；当水侵速度增大到一定值后，水侵速度成为主导因素，见水时间减小程度相对变缓。

图9 W井水侵速度对见水时间的影响

3.6 气井产量与气相非达西效应

气井产量、气相非达西效应对见水时间的影响见图10。由图10可知，随气井产量增大，见水时间逐渐减小，气井产量较小时，见水时间减小较慢；当气井产量增大到一定值后，见水时间迅速减小；非达西效应对见水时间几乎没有影响。这是由于初始气井产量较小时，水质点的驱动力小于重力分量，没有舌进速度，见水时间仅与水侵速度有关；随气井产量增大，水侵速度也增大，见水时间减小；随气井产量的继续增大，气体渗流速度增大，使水质点产生舌进速度并逐渐增大，同时临界边界增大，水质点舌进距离增大，使见水时间减小。由于水平井的泄气区较大，导致气体渗流速度不够大，气相非达西效应表现不明显，对见水时间的影响较小。

图10 W井气井产量、气相非达西效应对见水时间的影响

3.7 敏感程度

对重要影响因素进行无因次分析，定义向前、向后变化因数表示某种影响因素对见水时间的敏感程度。影响因素的取值范围为实际生产过程中的常用数值，取平均值作为变化基准值，将见水时间与影响因素变化程度的比值定义为变化因数，计算某种影响因素的向前、向后变化因数。取绝对值最大的变化因数作为该种影响因素的敏感程度因数，对所有影响因素进行强弱排序，结果见表2。由表2可知，影响水平井见水时间的主要因素由强到弱依次为气井产量、水侵速度、水平井与气水边界的初始距离、储层有效厚度、储层倾角和水平井长度。

表2 影响因素敏感程度分析

4 结论

(1)边水气藏水侵过程中，水质点既有水侵速度，又有舌进速度，计算见水时间时应考虑两种速度的迭加，存在一个临界边界将整个水侵过程分为纯水侵阶段和水侵迭加舌进阶段。

(2)考虑水侵速度、储层倾角及气相非达西效应，建立边水气藏水平井见水时间预测模型，计算结果的相对误差为-5.9%，验证模型可靠性。

(3)应用见水时间预测模型对重要影响因素进行敏感性分析，对气井见水时间产生正向影响的因素为储层有效厚度、储层倾角、水平井长度、水平井与气水边界的初始距离；产生负向影响的因素为水侵速度及气井产量；气相非达西效应对见水时间几乎没有影响。影响因素对水平井见水时间的影响程度由强到弱依次为气井产量、水侵速度、水平井与气水边界的初始距离、储层有效厚度、储层倾角和水平井长度。