事件触发机制下离散分布时滞Markov跳变网络化系统故障检测

李艳辉, 冀广超, 张国旭

(1.东北石油大学 环渤海能源研究院，河北 秦皇岛 066004; 2.东北石油大学 电气信息工程学院，黑龙江 大庆 163318)

0 引言

Markov跳变系统利用马尔可夫链的动态建模特性，描述系统受环境影响或其他外部因素引起的结构或参数的突变。Markov跳变系统可以模拟多个实际系统，如化工反应过程、太阳能发电系统、飞行控制系统和网络控制等[1]。因此，Markov跳变系统受到广泛关注[2-4]。DE SOUZA C E[5]研究具有Markov参数跳变的离散不确定线性系统的鲁棒稳定性问题。对于通信链路不可靠的非线性Markov跳变系统，ZHANG M等[6]研究模糊控制问题，并将设计的模糊控制器应用到机械臂中，获得优异的控制效果。

随网络化控制系统在工业生产过程中广泛应用，网络信息传输过程出现时延及数据包随机丢失等情况，降低系统的性能，甚至导致系统故障[7]。在实际的生产过程中，及时发现故障信息非常重要。DONG H L等[8]研究具有未知转移概率、随机非线性和传感器饱和的离散Markov跳变网络化系统的故障检测问题。对于在网络环境下具有执行器故障的Markov跳变系统，LONG Y等[9]研究有限频域异步故障检测和隔离策略。LI X J等[10]研究随机系统下的故障检测问题。在这些研究成果中，大部分考虑时变时滞，而分布时滞在离散时间域中正确定义，以及进行相应的数学分析等复杂性问题被忽视。分布时滞更能准确反映事物本质上的特点[11]，广泛应用于压力进料系统、反应堆燃烧过程等[12]。

由于网络通信带宽限制，通讯资源有限。传统的时间触发机制选取的采样周期很小，导致频繁进行数据传输和更新，以及通信资源被很多不需要传输的数据浪费。事件触发机制只在控制系统需要更新数据调整控制律时，传感器才对系统的输出进行采样和传输并更新控制信号，有效减少对有限通讯资源的占用，提高信息传输的效率[13-14]。考虑非线性反馈控制系统，DOLK V S等[15]提出一种新的事件触发控制策略，以保证有限的Lp增益和事件时间的严格正下界。PREMARATNE U等[16]提出一种事件触发的自适应差分调制方法，将事件触发的带宽缩减策略和语音编码技术相结合。基于H∞控制和事件触发通信协同设计问题，PENG C等[17]提出一种事件触发通信方案和采样状态误差依赖模型。事件触发方案应用于网络故障检测的相关问题研究受到越来越多的关注[18-19]。对于离散线性NCSs的故障检测问题，ZHANG Z H等[20]提出一种基于事件触发机制的区间观测器方法，通过考虑扰动和事件误差的影响而产生上下误差。为减轻有限网络带宽的使用，GU Y等[21]研究具有有限频率规格的离散利普希茨非线性系统的事件触发故障检测滤波器设计问题。面对越来越多网络化系统中更加复杂的被控对象，采用事件触发机制提高信息在网络信道中的传输效率需要进一步研究。

网络控制系统中存在的带宽限制增加网络数据计算量，系统故障问题影响控制系统的性能。对于具有离散分布时滞的Markov跳变网络化系统，笔者设计事件触发条件选择在不同的跳转模态下要传输的输出信号，采用阈值逻辑法对系统出现的故障信号进行检测判别，构造加权故障检测滤波器提高检测精度。在事件触发机制下，通过Lyapunov稳定性理论和随机理论得出故障检测系统随机稳定且满足H∞性能的准则，采用LMI技术和凸优化求解算法，结合数值仿真，验证设计故障检测方案能达到故障检测性能水平且有效减少带宽占用，提高信息传输效率。

1 问题描述

考虑具有时变时滞的离散Markov跳变网络化系统[22]：

(1)

设计故障检测滤波器得到Markov跳变网络化系统的残差信号，检测系统的故障为

(2)

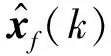
为有效利用网络资源,采用事件触发条件为

(3)

式中：ε为设定事件触发阈值；W为权值矩阵。对于所有的{kl}l=0,1,2,…网络传输时刻，当k∈[kl,kl+1)满足ey(k)=y(kl)-y(k)。

(4)

(5)

设计故障加权模型增强故障检测系统的检测性能，f(z)=W(z)f(z)表示加权模型，W(z)为加权矩阵。

(6)

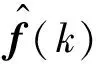
(7)

引理1[24]设M∈Rn为矩阵，xi∈Rn和常数ai≥0(i=1,2,3,…)，满足不等式

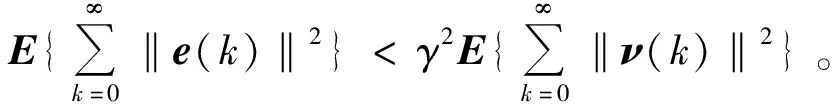
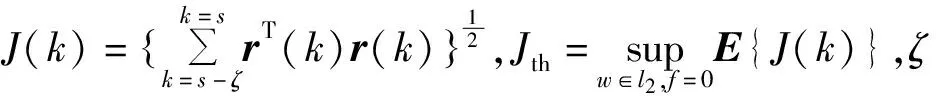
注1在实际的网络系统中，测量信号往往因为信道带宽限制、瞬间震荡、网络阻塞、缓存区溢出或传感器间歇失效等情况发生数据丢包现象，系统的故障检测滤波器的实际输入与控制系统的测量输出产生偏差，且在事件触发策略下没有满足触发条件的数据被丢弃。因此，故障检测滤波器的实际输入用式(4)表示。

2 故障检测系统的鲁棒H∞性能分析

建立故障检测系统式(8)在事件触发机制下的随机稳定且具有给定H∞性能指标γ的充分条件，为后续故障检测滤波器的设计提供理论依据。

定理1根据离散网络系统式(1)，给定标量γ>0，εi>0，α∈(0,1)和τM>τm>0，若有实矩阵Pi>0，Z>0，Wi>0使下列不等式成立：

(8)

(9)

此故障检测系统式(7)满足给定H∞性能指标γ且是随机稳定的。

证明选取Lyapunov 函数为

为处理系统中的时滞项，V2、V3、V4的选取与时滞相关。当k∈[kl,kl+1)，ϑ(k)=i且ϑ(k+1)=j时, 沿系统状态求差分，可得当ϑ(k)=i,i∈ϖ时，并对E{ΔV4(k,η(k))}应用引理1, 有

E{ΔV1(k,η(k))}=E{V1(k+1,η(k+1))-V1(k,η(k))}=

E{ΔV(k,η(k))}+E{‖e(k)‖2}-γ2‖ν(k)‖≤E{ΔV(k,η(k))}+

(10)

其中Ω同式(8)，从而可得E{ΔV(k,η(k))}<0。考虑当ν(k)=0时，故障检测动态系统式(7)，可得

E{Vk+1(η(k+1),ϑk+1)|(η(k),ϑk=i)}-Vk(η(k),ϑk=i)≤-λmin(Γi)ηT(k)η(k)≤-ληT(k)η(k),

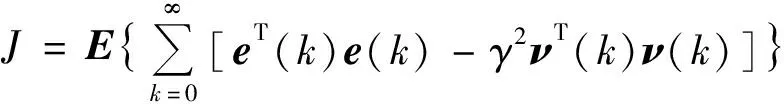
注2根据设计的Markov跳变网络化系统选取时滞依赖的Lyapunov-Krasovskii泛函，且将离散时变时滞的下界取为τm，相对于时滞下界为0的情况，降低系统的保守性。

3 故障检测系统的鲁棒H∞滤波器设计

采用等效变量替换法得出基于定理1的故障检测滤波器和事件触发权值矩阵参数求解算法。

定理2针对离散网络系统(1)，给定常数ε>0和α∈(0,1)，如果有正定对称矩阵Si>0、U1i>0、U2i>0、R11>0、R12>0、R22>0、R13>0、R23>0、R33>0、Z11>0、Z12>0、Z13>0、Z22>0、Z23>0、R33>0、W>0和矩阵AF、BF、CF、DF，以及常数γ>0存在，保证矩阵不等式成立：

(11)

则事件触发机制下的故障检测系统(8)随机稳定且满足H∞性能准则。

注3在事件触发机制下的故障检测问题可以转化为凸优化问题，得满足H∞性能指标的最优解:

minγsubject

(11)

4 仿真实例

考虑具有分布时滞的离散Markov跳变网络化系统(1)，系统两种模态ϖ={1,2}，模态切换马尔可夫过程转移概率为

系统的其他参数见模态1和模态2。

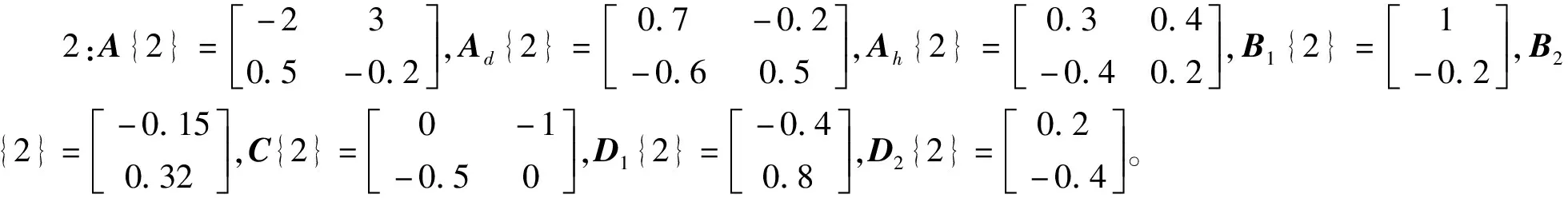
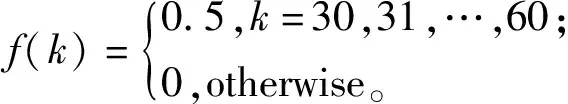
表1 当时，事件触发阈值ε和H∞性能等级γ之间的关系

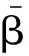
表2 当ε=0.2时，网络丢包参数和数据传输率re之间的关系

100个采样时刻下，仿真实例Markov模态的跳变过程见图1，其中‘1.0’为第一个子系统，‘2.0’为第二个子系统。仿真实例残差信号见图2，其中红色虚线表示无故障时的残差函数，蓝色实线表示有故障的残差函数。由图2可以看出，k=30时刻点发生故障,残差函数发生明显变化,100个采样时刻残差评价函数和阈值见图3。由图3可知，事件触发机制下故障检测系统的检测阈值为Jth=0.325 7，当系统中故障发生时J(30)=0.335 2>Jth，残差评价函数在k=30时刻有明显变化，表示故障信号发生并被检出，从而实现故障检测的目标。100个采样时刻事件触发机制网络数据传输数据与传统时间触发机制对比见图4。由图4可以看出，数值仿真模拟传输时间为100个采样时刻，传统的时间触发采样需要100个采样时刻系统测量数据，而事件触发机制下有82个有效数据被传输到故障检测滤波器，利用82个测量数据达到故障检测的目的。为与文献[10]中未引入事件触发机制的故障检测方案进行对比，将数值仿真模拟传输时间定为200个采样时刻，其结果分别见图5和图6。由图6可知，本设计仅需160个测量数据传输到网络中便可实现故障检测的目的，而文献[10]需要将全部200个测量数据输送到网络中。图4和图6的对比结果见表3。

图1 模态跳变过程

图2 仿真实例残差信号

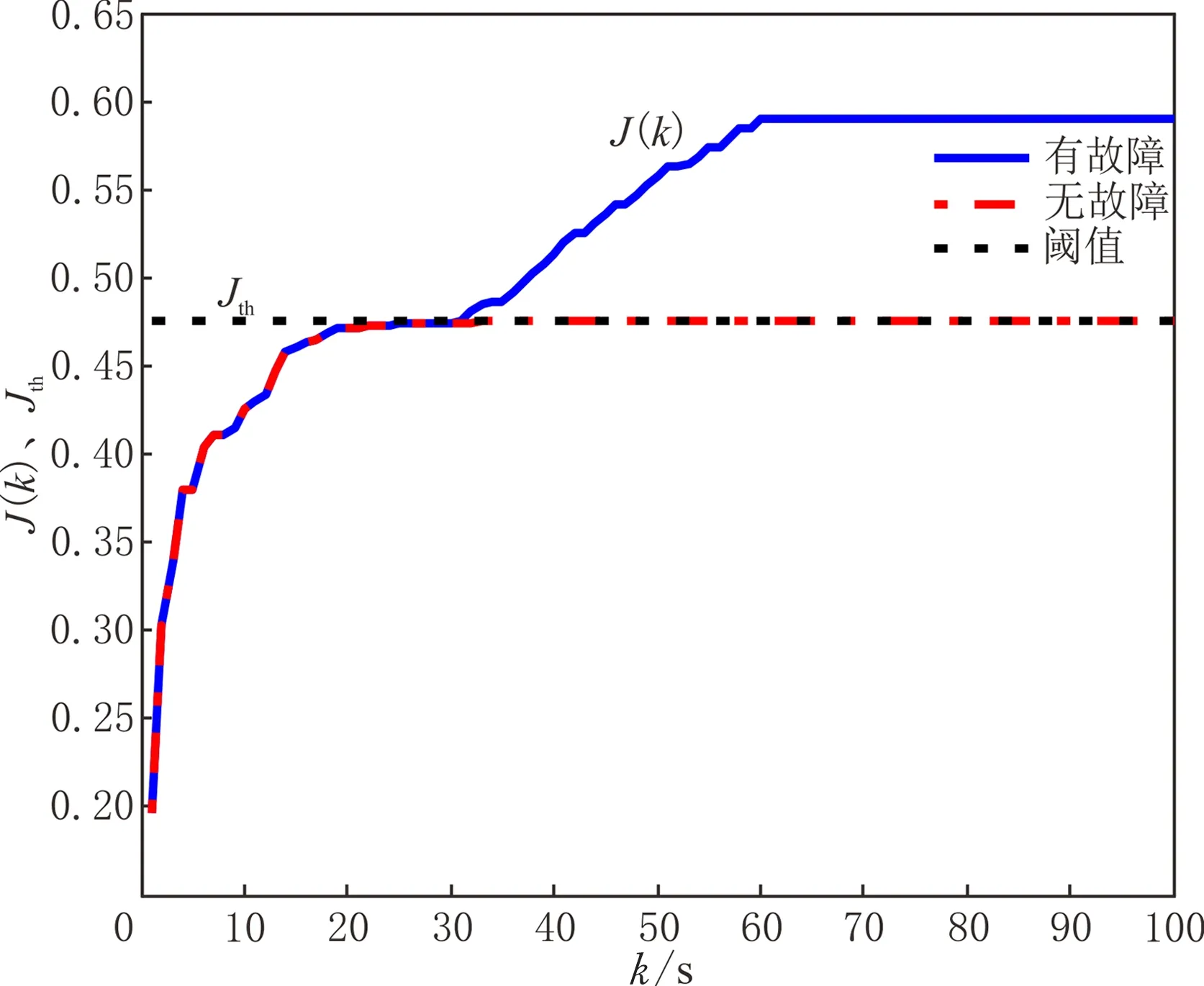
图3 100个采样时刻残差评价函数和阈值

图4 情况1(100个采样时刻)事件触发与时间触发时刻和间隔

图5 200个采样时刻残差评价函数和阈值

图6 情况2(200个采样时刻)事件触发与时间触发的时刻和间隔

表3 事件触发与时间触发网络数据包传输量对比

因此，采用事件触发机制提高网络信道中信息传输的效率，节省有限的网络带宽，保证故障检测系统有良好的故障检测性能。

5 结论

(1)对于具有分布时滞的离散Markov跳变网络化系统，设计一种事件触发故障检测方案在系统不同的跳转模态下选择要传输的输出信号，有效节省通信资源，减少数据传输网络的带宽占用。

(2)利用阈值逻辑法，设计事件触发机制下的加权故障检测滤波器保证故障检测系统更加快速地检测识别故障信号，考虑系统中出现的数据随机丢包及传输时延问题，选取时滞依赖Lyapunov函数，推导故障检测系统随机稳定的充分条件，利用凸优化求解算法得出故障检测滤波器参数，降低系统保守性。