基于扰动补偿的多源受扰系统反步控制设计

姜福喜,周兰,高东旭,潘昌忠,熊培银

(湖南科技大学信息与电气工程学院,湖南湘潭 411201)

1 引言

在控制工程中,欠驱动机器人[1]、电液伺服系统[2]、小型无人直升机[3]等实际控制系统中不可避免地存在未建模动态、参数摄动、外部扰动以及测量噪声等多类型、多来源的干扰,这些干扰的存在严重影响系统的控制性能.受目前加工技术水平和生产制造成本的限制,通过改变机械结构的方式来提高系统在复杂环境下的控制精度往往收效甚微.因此,研究设计先进控制算法对系统中的扰动进行抑制或补偿以提高系统的控制性能具有重要的科学意义.

根据扰动在系统中的分布情况,通常可将扰动分为匹配扰动与非匹配扰动,所谓匹配扰动是指扰动与控制输入在同一通道,反之,则为非匹配扰动.目前针对匹配扰动的抑制方法已有大量的研究,例如自抗扰控制中利用扩张状态观测器(extended state observer,ESO)在线估计和补偿控制输入通道中的总扰动,以实现对系统内、外干扰的主动抑制[4–6].此外,滑模变结构控制[7–8]、不确定干扰估计器[9–10]等控制方法也常用于解决此类匹配扰动的抑制问题.文献[11]针对非匹配扰动抑制问题,提出了基于广义扩张状态观测器(generalized extended state observer,GESO)的扰动估计方法,通过设计合适的扰动补偿增益,有效消除了非匹配扰动对系统输出的影响.但是对于具有多个扰动源的实际控制系统,通常既含有匹配扰动又含有非匹配扰动,以上处理单一匹配扰动或非匹配扰动的方法不再适用.

反步控制是一种常用的非线性控制方法,其核心思想是将非线性系统分解为多个低阶子系统,并为每个子系统设计Lyapunov函数与虚拟控制输入,保证各个子系统的镇定,通过多步递推计算完成系统实际控制规律的设计[12–13].传统反步控制对系统模型的准确性要求比较高,控制精度易受参数不确定性和未知外扰的影响.基于此,有研究将反步法与主动扰动抑制方法相结合,以提高反步控制系统的鲁棒性.特别是当扰动不满足匹配条件时,结合了主动抗干扰机制的复合反步控制方法具有明显的优越性[14].

文献[15]针对存在多源扰动的电液伺服系统,设计线性ESO估计系统不可测状态和匹配扰动,对于非匹配扰动则由非线性扰动观测器进行在线估计.文献[16]将积分反步控制和多个扰动观测器结合使用,实现了对多通道干扰的实时估计与有效补偿.文献[17]利用反步控制思想,将一类具有下三角结构的高阶系统划分为多个一阶子系统,然后分别针对每个子系统设计降阶扩张状态观测器(reduced-order extended state observer,RESO),实时估计各个子系统中的总扰动并加以补偿,增强了系统的抗扰能力.进一步地,文献[18]将该方法应用于自动导航车辆,实现了对未知摩擦和车轮打滑等不确定性的有效补偿.然而,上述几种处理多通道扰动的控制方法需要设计多个观测器来估计各个通道中的扰动,增加了系统结构的复杂度与参数调节难度,并且繁重的计算量很容易导致控制执行器延迟.

针对以上问题,本文提出基于降阶广义扩张状态观测器(reduced-order generalized extended state observer,ROGESO)的多源受扰系统反步控制设计方法.通过构造ROGESO对多源扰动进行同步实时估计,利用扰动估计值设计基于扰动主动补偿的复合反步控制律,有效抑制扰动对系统输出的影响,从而实现系统输出对参考输入信号的高精度跟踪.本文的主要创新点如下:1)充分利用系统信息,设计一个ROGESO在线估计各个通道的扰动,有效降低一般主动扰动抑制方法中使用全维状态观测器引起的相位滞后;2)设计基于扰动补偿的指令滤波(command filter,CF)反步控制律,同时消除匹配和非匹配扰动对系统输出的影响,保证系统具有满意的过渡过程性能、稳态性能和鲁棒性.

2 问题描述

考虑如下n阶多源受扰系统:

其中:ai,i+10,i=1,2,···,n −1,b为已知非零常数,In表示n阶单位矩阵.设系统参考输入为r(t),假定r(t)和光滑,有界并且已知.

系统(1)可以描述实际工程中常见的多源受扰系统,例如电液伺服系统[15],双轴伺服系统[20]等,其中fi(t)(i=1,2,···,n −1)与u(t)不在同一通道,为非匹配扰动,fn(t)为匹配扰动.

假设1系统(1)中各通道总扰动fi(t)及其一阶导数有界,即满足

其中Ψi和Φi为未知正数.

本文的控制目标为:针对多源受扰系统(1),设计基于ROGESO的指令滤波反步控制规律,通过对各通道的总扰动进行实时估计与动态补偿,使系统稳定,并保证输出对参考输入信号的高精度跟踪.

3 基于ROGESO的指令滤波反步控制系统设计

本节将给出ROGESO的结构和指令滤波反步控制器的设计步骤.基于ROGESO的指令滤波反步控制系统结构如图1所示.

图1 基于ROGESO的指令滤波反步控制系统结构Fig.1 Configuration of the ROGESO-based command filtered backstepping control system

3.1 构造ROGESO

引入扩张状态变量

建立系统(1)的增广模型

由于系统(1)的状态xp(t)可测,本文仅需设计观测器对各个通道的扰动进行估计.将增广系统(3)中的可测变量与不可测变量分离得到

联立式(2)(5),建立降阶增广系统状态空间模型

针对系统(6),设计如下状态观测器:

3.2 基于多通道扰动主动补偿的复合反步控制律

本小节采用反步法递归设计虚拟控制律,并将ROGESO(9)得到的各通道扰动估计值引入到对应子系统的虚拟控制律中进行反向补偿,实现各级子系统的镇定,并保证系统输出对参考输入信号的高精度跟踪.

步骤1设x1d(t)=r(t)为被控系统的期望输出,针对系统(1)的x1–子系统,分别选取状态跟踪误差

和Lyapunov函数

对V1(t)求导,并引入虚拟控制输入α1(t)得到

将α1(t)设计为

其中k1∈R+为待选取的反步控制增益.将式(13)代入式(12)得到

其中:zi(0)=αi(0),zi+1(0)=0,zi(t)和zi+1(t)为滤波器状态,x(i+1)d(t)为滤波器输出,0<ζ≤1,ωn>0分别为滤波器的阻尼比和自然频率.

由式(15)得x(i+1)d(t)与αi(t)的传递函数为

注1由式(15)和图2可知虚拟控制输入αi(t)的一阶导数估计值可由积分过程得到,从而避免了传统反步控制对虚拟控制输入直接求导而放大噪声.此外,当被控系统的阶数较高时,传统反步控制存在反复求导引起的计算膨胀问题,采用于基于二阶指令滤波器的反步控制可大大减少计算量.

图2 二阶指令滤波器结构图Fig.2 Structure block diagram of the second-order command filter

注2本文采用指令滤波器逼近各子系统的虚拟控制输入及其一阶导数,参考输入信号r(t)及其一阶导数满足光滑有界条件即可,放宽了传统反步控制系统对参考输入信号n阶连续可导的要求[19].因此,与传统反步控制相比,本文设计的指令滤波反步控制方法应用范围更广.

步骤m(m=2,3,···,n−1) 针对系统(1)中的xm–子系统,分别选取状态跟踪误差

和Lyapunov函数

其中:ki∈R+为待选取的反步控制增益,εi(t)=x(i+1)d(t)−αi(t),表示第i次滤波产生的滤波误差.

将αm(t)设计为

其中km∈R+为待选取的反步控制增益.将式(20)代入式(19)得到

步骤n针对系统(1)的xn–子系统,分别选取状态跟踪误差

和Lyapunov函数

对Vn(t)求导可得

其中kn∈R+为待选取的反步控制增益.

4 系统稳定性分析

本节将给出本文所提控制方法的稳定性证明,说明系统(1)在第3.2节的反步控制律作用下有界稳定.

定理1在满足假设1的条件下,通过选取合适的观测器增益矩阵L,使得矩阵−为Hurwitz矩阵,则可保证扰动估计误差动态系统(8)渐近稳定,并且扰动估计误差ef(t)指数收敛至球界.

成立.设λmin(K)为矩阵K的最小特征值,Φmax为所有通道扰动一阶导数的最大上界.

选取Lyapunov函数

对V0(t)求导

注3由以上分析可知,当扰动的一阶导数为零即Φmax=0时,ROGESO可实现对各通道扰动的稳态无偏差估计.

引理1考虑二阶指令滤波器(15),若假设1成立,则对于给定任意小的正实数χ,存在充分大的滤波器自然频率ωn,使得滤波误差|zi(t)−αi(t)|≤χ对于任意t≥0恒成立[12].

5 仿真研究

考虑如下具有参数不确定性和外部负载干扰的S60BL-430型无刷直流电机伺服系统[22]:

其中:ω(t)为电机转子的角速度,i(t)和u(t)分别为电枢电流和控制输入电压,Mc(t)表示外负载转矩,其他参数定义及标称值列于表1.

表1 无刷直流电机参数Table 1 Parameters of the brushless DC motor(33)

电机在运行过程中受摩擦、涡流等因素的影响,其内部温度会发生变化,由此导致电枢绕组的相电阻R和相电感Ls产生参数摄动.另一方面,外部负载的变化会引起转子转动惯量J的摄动.设上述参数不确定性满足关系式

其中:R0,L0,J0分别是相电阻、相电感和转动惯量的标称值,R0∆R,L0∆L,J0∆J分别是相电阻、相电感和转动惯量的摄动量.

选取状态变量xp(t)和控制输出yp(t)分别为

建立系统(1)形式的无刷直流电机伺服系统状态空间模型,相应的系数矩阵和各通道扰动为

5.1 观测器估计性能对比分析

由前面的分析可知,多通道干扰的估计精度将直接影响系统的扰动补偿效果和跟踪精度.本小节针对系统(33),从频域的角度分析ROGESO的扰动估计性能,并与文献[11]中的全阶GESO对比.

设ROGESO(9)中的观测器增益矩阵L为

设全阶GESO[11]的观测器增益矩阵Γ为

类似地,由全阶GESO的估计误差动态方程得到各通道扰动估计值与实际扰动fi(t)(i=1,2)的传递函数分别为

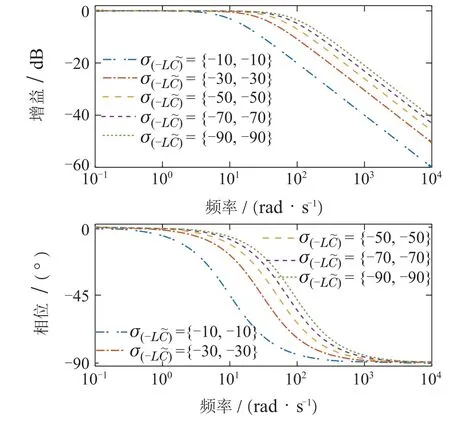
图3 不同极点条件下GROGESO(f1)(37)的伯德图Fig.3 Bode diagram of GROGESO(f1)(37)with different poles

图4 ROGESO和GESO的扰动估计传递函数伯德图Fig.4 The Bode diagram of the disturbance estimation transfer function for ROGESO and GESO

5.2 仿真结果对比分析

设式(34)中的参数不确定性具有如下形式:

外负载转矩和参考输入信号分别为Mc(t)=0.1sin(0.5πt)+0.25sin(πt)+arctan(0.2t),r(t)=(100sin(πt)+80sin(0.5πt))(1−exp(−t)).

选取反步控制器增益k1=50,k2=1.2;二阶指令滤波器(15)中ζ=0.1,ωn=200;ROGESO(9)的极点={−45,−45},得到观测器增益矩阵

图5为ROGESO对各通道扰动的估计以及相应的估计误差曲线.可见,本文设计的ROGESO可以准确估计各通道扰动,其中f1(t)的最大稳态估计误差约为其实际值的1.2485%,f2(t)的最大稳态估计误差约为其实际值的8.8911%.图6为指令滤波器(15)对虚拟控制输入α1(t)(13)的估计曲线,最大稳态估计误差为0.0031,因此,该滤波器具有较好的估计性能.

图5 ROGESO(9)对f1(t)和f2(t)的估计Fig.5 Estimation curves of f1(t)and f2(t)

图6 指令滤波器(15)对虚拟控制输入α1(t)的估计Fig.6 Estimation curve of the command filter (15) for the virtual control input α1(t)

图7为本文设计的基于ROGESO的指令滤波反步控制系统的输出响应曲线,其中系统最大稳态跟踪误差约为1.2459×10−4.具体性能指标列于表2,其中tp为上升时间,ess为最大稳态跟踪误差,最大PTP表示稳态跟踪误差的最大峰值与谷值之差,uss表示最大稳态控制输入电压.结合表2可知,该伺服系统可以准确估计并有效补偿各通道扰动,保证电机的输出转速高精度跟踪参考输入信号r(t).

图7 基于ROGESO的无刷直流电机反步控制系统输出响应Fig.7 Output response of the ROGESO–backsteppingbased brushless DC motor servo system

表2 性能指标对比Table 2 Performance indicators

图8为相同控制器参数下本文所提方法与基于全阶GESO的反步控制(GESO–backstepping)系统扰动估计误差和系统跟踪误差对比.结合前面的频域分析可知,相比于全阶GESO,ROGESO引起的相位滞后更小,扰动估计和补偿效果更好.由表2可知,本文所提方法下的伺服系统最大稳态跟踪误差约为GESO–backstepping系统的46.5079%,因此,本文方法下的系统跟踪性能与抗扰性能更佳.

图8 本文方法与基于GESO的反步控制对比Fig.8 Comparisons between the proposed method and the GESO-based backstepping control system

图9为本文所提控制方法与文献[17–18]提出的基于RESO的反步控制(RESO–backstepping)及常规反步控制系统跟踪误差对比.结合表2可知:1)与常规反步控制系统相比,引入主动抗干扰机制的RESO–backstepping系统和本文设计的系统扰动抑制性能更强,跟踪误差更小;2)本文控制方法下的系统过渡过程性能、稳态性能以及鲁棒性均明显优于其他两种方法.

图9 本文方法与常规反步控制以及基于RESO的反步控制[17–18]跟踪误差对比Fig.9 Comparisons of tracking performance of the proposed method,conventional backstepping control and RESO-based backstepping control[17–18]

6 结论

本文针对存在多通道状态相关不确定性和外部干扰的多源受扰系统,提出了基于ROGESO的反步控制设计方法,证明了闭环系统的有界稳定性.仿真结果表明,所设计的控制系统可实现对各通道扰动的在线估计与动态补偿,保证系统对参考输入信号的高精度跟踪.通过时域和频域的仿真分析比较发现,所提方法的系统过渡过程性能、稳态跟踪性能和扰动抑制性能优于基于全阶GESO的反步控制、基于RESO的反步控制、以及常规反步控制方法.