基于凸空间收缩滤波的噪声不确定时滞系统状态估计

王子赟 李南江 王艳 纪志成

(1.江南大学轻工过程先进控制教育部重点实验室,江苏无锡 214122;2.江南大学物联网技术应用教育部工程研究中心,江苏无锡 214122)

1 引言

在复杂的工艺系统和一些信号处理系统中,由于外界因素多变、系统工况复杂等原因,这些系统往往存在时滞问题,例如输入信号时滞、传感器传输时滞、信号网络传输时滞等[1–4],从而带来系统震荡、功能退化甚至失去其稳定性等不良影响.现有的系统状态估计研究成果主要针对线性离散系统,相较而言对含时滞的系统研究较少.近年来,针对时滞现象的系统状态估计问题也逐渐受到学者们的关注[5–7].

针对含时滞的系统状态估计问题,当前的研究主要是利用状态扩维方法,将系统转化为不含时滞的增广系统[8].这类方法虽然简便,但是会不可避免地增加系统的维数,从而导致算法的计算复杂度增加.刘飞等[9]针对含状态时滞的线性离散时变系统,提出了一类无偏有限脉冲响应滤波算法.通过构造含有时滞状态的增广系统模型,对原系统进行无时滞转换.此外,H∞滤波也是求解时滞系统状态估计的一类常用方法.肖会敏等[10]针对一类具有外部扰动的不确定广义时滞系统,设计了H∞状态估计器进行状态估计;齐迹等[11]针对含有随机时变时滞的网络化切换控制系统,采用满足Bernoulli分布的随机序列描述时变时滞现象,基于李雅普诺夫方法给出了H∞性能指标的充分条件.

以卡尔曼滤波[12–13]为代表的基于噪声信号概率分析方法,是解决系统状态估计问题最主流的研究路径.这些方法都需要预先假设噪声为满足某一分布规律,或者已知噪声的部分或全部特性.然而,实际工业系统受到的噪声是无法采用某一先验分布规律精确描述的,因此,传统的基于噪声信号概率分析的状态估计方法在解决这类不确定系统状态估计问题时,效果往往不好.集员方法是通过采用规则化空间结构,对系统状态进行包裹,求解状态估计问题过程中仅需要已知噪声或干扰的上下界,不需要预设噪声信号的先验分布规律,适用性更广,因此在状态估计、故障诊断、电子系统等许多领域都得到了广泛运用.例如,文献[14]研究了零初始状态下的系统状态估计问题.Li等[15]将可行集估计的目标定义为在零初始条件下确定包含系统所有状态可行集合的有界椭球,这个定义忽略了初始状态值不同所带来的影响,仅仅在稳态情况下可行.近些年来也有一些学者研究非零初始状态下时滞系统的可行集估计,并将其用于反馈控制器设计,比如Nam等[16]将可行集估计应用于输出反馈控制器设计.集员方法的一个关键之处在于针对可行集的形状描述如何更加准确,目前来描述可行集的方法主要有椭球[17–19]、正多胞体[20]、区间[21]、全对称多胞体[22–23]等.沈艳霞等[24]提出一种基于凸多面体的集员滤波方法,利用包含所有参数可能存在的凸多面体,结合Fourier-Motzkin消去法实现了对系统的状态估计.文献[25]提出了一种基于最优定界椭球的状态估计方法,借鉴了标准化椭球形状结构包裹零初始条件下的时滞系统真实状态,然而该方法带来的椭球空间冗余度高,难以得到紧致的时滞系统状态估计集合.

本文针对噪声不确定时滞系统,提出一种基于凸空间收缩滤波状态估计方法,通过构造包裹时滞系统当前状态的凸空间结构,实现凸空间包裹下的状态预测和量测更新.本文所提方法与文献[25]提出的最优定界椭球算法相比,省略了部分约束条件,空间结构描述形式更简单且不失保守性.同时,本文所采用的凸空间体相比于传统椭球结构而言,降低了计算复杂度的同时,能够更加紧密贴合实际的系统状态可行集.

2 问题描述

首先定义本文所用的一些符号.|X|∞表示向量X的无穷范数,|x|表示元素x的绝对值;a∈A表示a属于集合A,或者称a是集合A中的元素;A⊆B表示集合A是集合B的真子集;A−1表示可逆矩阵A的逆,AT表示向量或矩阵A的转置,Ai表示矩阵A的i次幂;I表示单位矩阵,A:=B表示用矩阵A指代或定义矩阵B.

考虑如下的噪声不确定时滞系统:

其中:x(k)∈Rn,y(k)∈Rm,u(k)∈Rr分别是k时刻系统的状态量、输出量和输入量;A∈Rn×n,Ah∈Rn×n,B∈Rn×r,D∈Rn×q,C∈Rm×n均为已知矩阵;w(k)∈Rq,v(k)∈Rn分别为k时刻系统受到的干扰和测量噪声,h表示时滞时间长度.同时,定义下列中间变量:

假设1对于给定的噪声不确定时滞系统(1)和式(3),矩阵A,Ah和E均满秩.

假设2系统的干扰和噪声分别满足如下的未知但有界约束:

定义1定义包裹k时刻系统真实状态x(k)的凸空间体Set(Mk,αk):

其中:X(k)表示包含k时刻系统真实状态x(k)的状态可行集,Mk和αk表示k时刻凸空间体的形状矩阵和外界约束矩阵.

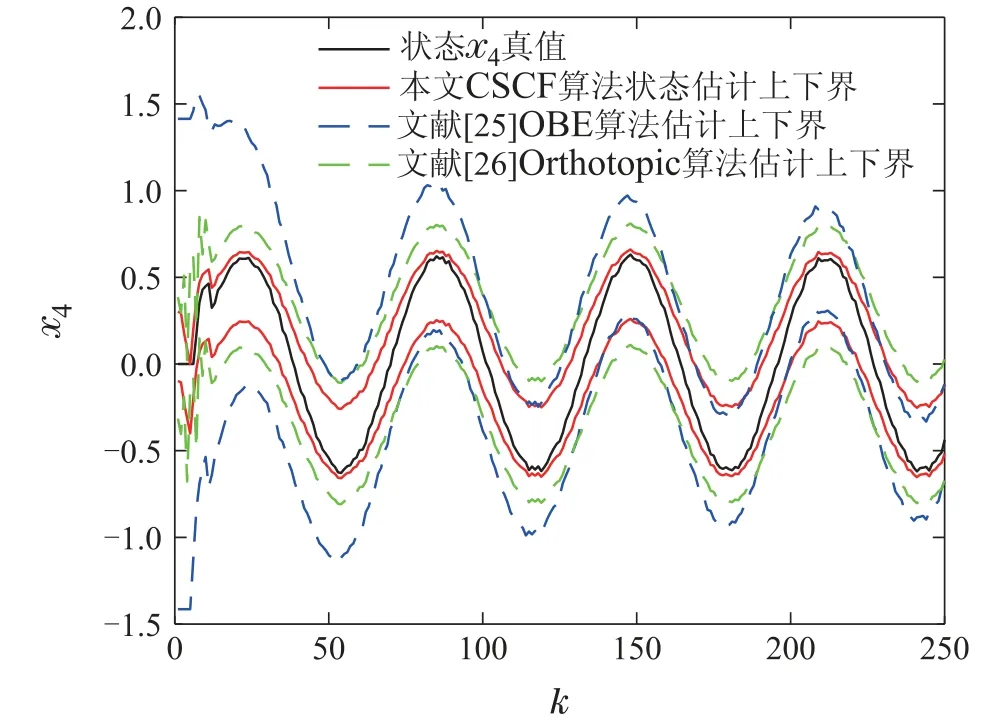
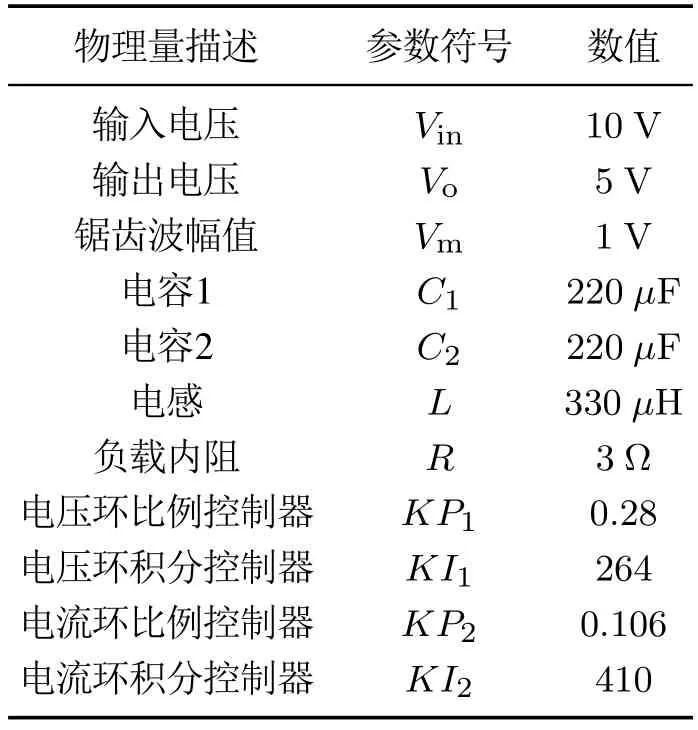
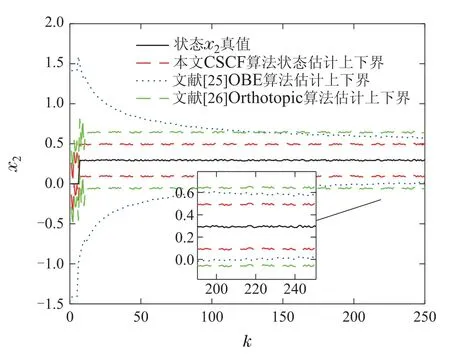
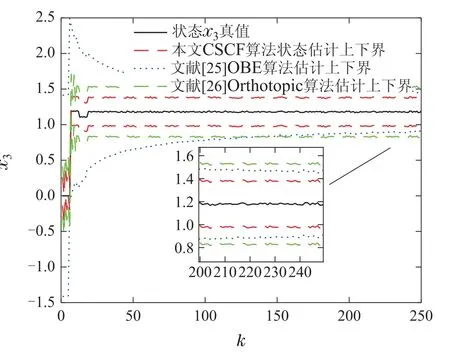
注1对于0

本文旨在针对噪声不确定时滞系统,考虑不确定噪声w(k)、不确定干扰v(k)和时滞信号的影响,从空间几何学角度,通过设计并求解规则且紧致的凸空间结构,进而包裹不规则的系统状态可行集,实现噪声不确定性时滞系统状态估计,降低状态估计可行集的冗余度.

3 主要结论

3.1 状态预测

本节的目的在于求解能够包裹k+1时刻的状态预测值的凸空间体.在k≥h时,对于噪声不确定时滞系统(1)而言,k+1时刻的状态预测值属于集合+1),即

下面给出包裹k+1时刻系统状态可行集的凸空间体存在性证明,推导该凸空间体的表示方法.

证对于系统(1),其k+1、k和k −h时刻的系统状态预测值可分别表示为

将式(12)–(13)代入式(11),可得

将式(3)–(6)定义的各矩阵变量代入式(14),那么k+1时刻的系统状态预测量可表示为

考虑到k −2h至k −h时刻之间的系统状态预测值均满足

且根据假设1,A,Ah,E均可逆,可定义

证毕.

3.2 量测更新

在前述对k+1时刻的系统状态预测基础上,下面从凸空间收缩角度,实现k+1时刻的状态量测更新.

定义k+1时刻包裹真实状态的带空间Sk+1为

考虑到包裹k+1时刻系统真实状态x(k+1)的可行集X(k+1),包含于式(18)所述带空间Sk+1和预测状态可行集之间的交集

由k+1时刻的系统预测状态可行集

可知

定理2对于噪声不确定时滞系统(1),k+1时刻包裹真实状态可行集X(k+1)的凸空间体Set(Mk+1,αk+1)为

其中:

证考虑到k+1时刻系统输出采样受到的扰动v(k+1)满足

将式(2)中k+1时刻系统输出量代入上式,可得

将式(26)–(27)代入式(24)–(25),整理后可得

依据定义1中给出的凸空间体结构,可知包含k+1时刻系统状态真值的凸空间体Set(Mk+1,αk+1)的形状矩阵为

其中:

证毕.

最后,利用MATLAB软件自带优化工具箱内的线性规划函数,求解式(29)所示的线性不等式组,通过不断迭代预测步和更新步的线性不等式,从而得到包裹各时刻系统状态真值的凸空间体及其上下界.

综上,本文针对噪声不确定时滞系统提出的基于凸空间收缩滤波状态估计算法运行步骤如下:

步骤1定义状态估计步数L和时滞量h,定义包裹初始状态的凸空间体Set(M0,α0),0 ≤k

步骤2根据输入量u(k)和已知状态矩阵,求解状态预测凸空间体约束(16)和(17),得到k+1时刻状态预测凸空间体

步骤3根据输出数据y(k)和已知观测矩阵,构造k+1时刻用于量测更新的凸空间体(26)–(27);

步骤4利用线性规划函数求解不等式组(29),得到k+1时刻包含系统真实状态的凸空间体上下界;

步骤5置k=k+1,判断k是否等于L.若k=L,算法结束,输出包裹系统状态的凸空间体Set(Mk,αk);否则,返回步骤2.

4 实例仿真

为了验证本文提出的基于凸空间收缩滤波状态估计方法的有效性,采用两个示例进行仿真验证.

例1考虑如下不确定时滞系统:

相关系统矩阵分别为

给定输入u(k)=1.5 sin(0.1k),h=5,其余初始状态与不确定扰动同样满足约束.将本文提出的CSCF算法与文献[25]以及文献[26]进行对比,仿真结果如图1–6所示.

如图1所示,在k=0∼50 范围内间隔10步分别获取凸空间和椭圆空间,黑色记号“×”表示当前时刻状态真实值,红色凸空间所包裹区域表示本文所提出的CSCF算法带来的状态可行集,蓝色椭圆形包裹区域表示利用文献[25]的OBE算法得到的状态可行集,绿色矩形包裹区域表示利用文献[26]的Orthotopic算法得到的状态可行集.由图1可以看出,随时间增加,3种算法均能够时刻跟随状态量变化而变化,相比而言,利用本文所提出的CSCF算法得到的区域更小,意味着保守性更好.

图1 状态估计递归演化对比Fig.1 Comparison of recursive evolution

由图2–5可以看出,3种方法的可行集上下界均能够实时包裹状态真实值,放大对比后可以发现,初始情况下,本文提出的CSCF算法收敛更快,OBE算法最终误差也和本文算法相似,而文献[26]的Orthotopic算法初始比OBE算法误差更小,最后则是误差更大,总之CSCF算法估计效果在不失精准的前提下收敛效果较好.

图2 状态x1估计曲线对比Fig.2 Comparison of state estimates on x1

图3 状态x2估计曲线对比Fig.3 Comparison of state estimates on x2

图4 状态x3估计曲线对比Fig.4 Comparison of state estimates on x3

图5 状态x4估计曲线对比Fig.5 Comparison of state estimates on x4

图6展示了在k=50,100,150,200等标志性时刻的凸空间和椭圆、正多胞体空间位置,以二维平面视角更加直观的展示仿真结果.黑色记号“×”表示当前时刻状态真实值,红色矩形所包裹区域表示凸空间体算法得到的可行集,蓝色椭圆所包裹区域表示文献[25]OBE算法得到的可行集,绿色四边形所包裹区域表示文献[26]Orthotopic算法得到的可行集.从图6中可以直观看出凸空间结构包裹区域相较于对比算法而言更小,体现了本文所提出的算法保守性更小.

图6 状态可行集对比Fig.6 Comparison of feasibility state sets

例2在动力电池化成工艺中,充放电恒流恒压以及间隔期间切换时,信号传输过程中的延时无法避免.下面针对图7所示的不确定干扰下带有时滞的双向DC-DC变换器系统,进一步验证本文提出的基于凸空间收缩滤波状态估计方法的有效性.

图7 含时滞的双向DC-DC变换器系统Fig.7 Bidirectional DC-DC converter system with time delay

化成充放电过程中的间隔和切换过程离散化后,可采用状态空间方程描述为

其中:x(k)=[icha(k)idis(k)vc(k)]T,icha(k)为充电时流经电感的电流,idis(k)为放电时流经电感的电流,vc(k)为变换器系统的输出电压.系统输入u(k)=[d1(k)d2(k) 0]T,其中:d1(k)为开关管Q1开关信号的占空比,d2(k)为开关管Q2开关信号的占空比.w(k)与v(k)为系统过程噪声,化成充放电过程状态空间方程中的已知矩阵为

系统具体参数如表1所示.

表1 双向DC-DC变换器参数Table 1 Parameters of bidirectional DC-DC converter

将表1中的变换器各参数代入化成充放电状态空间,可以得到该模型的已知矩阵如下:

同时设定B=[0.2 0.3 0.8]T,C=I3,D=[0.1 0.10.1]T,时滞步长h=5,开关管Q1和Q2的开关信号的占空比分别为0.1和0.2.针对电池化成充放电过程,本文采用所提出的CSCF算法和文献[25]的OBE算法以及文献[26]的Orthotopic 算法,得到的仿真结果如图8–12所示.

图8所示为在k=0∼50范围内间隔10步分别获取的凸空间和椭圆空间.黑色记号“×”表示当前时刻状态真实值,红色凸空间所包裹区域表示本文所提出的CSCF算法带来的状态可行集,蓝色椭圆形包裹区域表示利用文献[25]的OBE算法得到的状态可行集.绿色矩形包裹区域表示利用文献[26]的Orthotopic算法得到的状态可行集.

图8 电感充放电电流状态估计递归演化对比Fig.8 Comparison of recursive evolution of inductor charging and discharge current state estimation

由图9–11可以看出,3种方法带来的空间结构均能够实时包裹状态真实值,但无论是从电感充放电流估计递归演化情况,还是从电感充电、放电以及输出电压状态估计曲线,均能看出本文提出的CSCF算法带来的凸空间体包裹电流和电压状态上下界更小,保守性更低.

图9 电感充电电流状态估计对比Fig.9 Comparison of inductance charging current estimates

图12展示了在k=50,100,150,200等标志性时刻的凸空间和椭圆、正多胞体位置.黑色记号“×”表示当前时刻状态真实值,红色矩形所包裹区域表示凸空间体算法得到的可行集,蓝色椭圆所包裹区域表示文献[25]OBE算法得到的可行集,绿色四边形所包裹区域表示文献[26]Orthotopic算法得到的可行集.可以看出本文所提出的CSCF算法带来的凸空间能够更紧致的包裹电感充电和放电电流真实状态,空间冗余度更低.

图10 电感放电电流状态估计对比Fig.10 Comparison of inductance discharge current estimates

图11 输出电压状态估计对比Fig.11 Comparison of output voltage estimates

图12 电感充放电状态可行集对比Fig.12 Comparison of feasible state sets on inductance charge and discharge current

5 结论

本文针对不确定时滞系统的状态估计问题,提出了基于凸空间收缩滤波方法,利用未知但有界的噪声和干扰条件,将带时滞的系统模型展开后得到状态预测后的凸空间体,随后利用当前时刻的噪声构造有界带空间,依据同时满足预测步和更新步约束的线性不等式组,求解预测凸空间体和带空间的交集,利用线性规划得到时滞系统真实状态的上下界,最后采用数值仿真和电池化成工艺案例进行仿真验证,验证了方法的有效性.本文所提的基于凸空间收缩的滤波算法,需假定系统的部分矩阵满足可逆条件,如何进一步拓宽基于凸空间收缩的状态估计算法的适用领域还有待进一步研究.本文的研究成果可以结合凸优化、区间观测器设计等方法,推广至解决不确定噪声扰动下的时滞非线性系统状态估计[27]、故障诊断[28]及其控制器设计问题[29].