K近邻和加权相似性的密度峰值聚类算法

赵嘉 ,陈磊 ,吴润秀 ,张波 ,韩龙哲

(1.南昌工程学院信息工程学院,江西南昌 330099;2.全球能源互联网研究院有限公司,江苏南京 210003)

1 引言

聚类是数据挖掘和模式识别领域的热门话题,它是一种无监督学习,能够将数据按照一定规则划分为类簇,使得同一类簇样本是相似的,且与其他类簇的样本不相似.目前,聚类分析已在不同的学科领域得到广泛应用,如模式识别[1]、图像分析[2]、网络安全[3]和生物信息[4]等.近年来,人们从不同角度提出了许多聚类算法,主要包括基于划分的聚类算法、基于模型的聚类算法、基于层次的聚类算法和基于密度的聚类算法等.

基于划分的聚类算法将给定的数据集划分为多个类簇,建立基于划分规则的目标函数,并迭代寻优.虽然该方法简单有效,但它的聚类结果受噪声点的影响,且在非球形数据集上的聚类效果不佳.K-means算法[5]是最常用的基于划分的聚类算法.基于模型的聚类算法假设一个聚类的实例最可能来自于一个特别的概率模型,一般采用固定数量的模型来近似物体的分布.然而,这类算法在聚类之前,通常很难了解模型或描述数据分布.EM(expectation-maximization)算法[6]是这类算法的典型代表.基于层次的聚类算法通过自下而上或自上而下的方式递归地对数据进行分类来构建类簇,可以用树状图来表示.然而,层次聚类方法的聚类复杂度高、鲁棒性差,数据集小的改变就会导致层次树状图结构的较大变化.Chameleon算法[7]是一种典型的基于层次的聚类算法.基于密度的聚类算法旨在识别由较低密度区域分隔出的稠密区域,这些方法可以在特征空间中识别任意形状的非球形类簇.DBSCAN(density based spatial clustering of applications with noise)[8]和OPTICS(ordering points to identify the clustering structure)[9]是两个著名的基于密度的聚类算法.这些方法可以在特征空间识别出任意形状的非球形类簇,不需要对数据的分布做任何假设就可以估计类簇的密度.但是,它们对参数非常敏感,参数值的很小变化,会产生完全不同的聚类结果.

本文研究的是一种基于密度的聚类算法,即快速搜索和寻找密度峰值聚类算法[10],简称密度峰值聚类(density peaks clustering,DPC)算法.DPC算法由Rod-riguez和Laio于2014年在Science上提出,它通过样本的局部密度和相对距离确定类簇中心,然后将剩余样本分配给密度比它高且距离它最近的类簇.

流形数据通常由一些包含条状和环状类簇的数据组成,密度分布不均数据由类簇间疏密程度不一的数据组成.流形及密度分布不均数据广泛存在于人们的生产活动中,如图像分割、手写数字识别和web分析等[11].DPC算法利用样本的局部密度以及相对距离快速确定密度峰值,可以聚出任意形状类簇[12],但DPC算法仍然存在以下不足:1)在聚类密度分布不均数据时,算法的局部密度未考虑类簇间的样本疏密程度差异,易在密集类簇中寻找到多个密度峰值,而稀疏类簇中无密度峰值;2)DPC算法的分配策略依据欧氏距离通过密度峰值进行链式分配,而流形数据通常有较多样本距离其密度峰值较远,导致大量本应属于同一个类簇的样本被错误分配给其他类簇,致使聚类精度不高.

为解决DPC算法存在的上述问题,许多学者对其进行了改进.针对局部密度定义的缺陷,Xu等人[13]提出了一种具有密度敏感相似性的稳健密度峰值聚类算法.该算法引入密度敏感相似性代替欧氏距离,提高了流形数据的聚类效果,并消除了截断距离参数的选取对聚类结果的影响.陈俊芬等人[14]提出了一种复杂高维数据的密度峰值快速搜索聚类算法.该算法采用流行距离高斯核函数值的累加重新定义样本的局部密度,使潜在密度峰值成为最大值点,提高了同一类簇样本间的紧密性和不同类簇样本间的分离性.该算法在处理复杂高维数据时具有较好的鲁棒性.Xie等人[15]提出了一种基于模糊加权K近邻检测密度峰值并分配剩余点的聚类算法.该局部密度计算方式将范围从所有样本缩减为样本的K个近邻,更能体现样本的局部信息.以上算法均对DPC算法的局部密度进行了改进,提高了聚类效果,但对疏密程度相差较大的数据集,它们仍然难以准确找到密度峰值,致使聚类效果不佳.

针对分配策略设计的不足,赵嘉等人[16]提出了一种基于相互邻近度的密度峰值聚类算法,该算法定义了一种新的样本相互邻近度的度量准则,能够准确分配剩余样本,对密集程度不一数据具有较好的聚类效果.丁志成等人[17]提出了一种优化分配策略的密度峰值聚类算法.该算法参考万有引力公式,使用基于相似度的局部连通性对样本进行分配,提高了流形数据集上样本分配的准确度.胡恩祥等人[18]提出了一种基于密度峰值剪枝后的最短路径聚类算法.针对剩余点的分配,该算法从不同的密度峰值出发选择到达该点距离的最短路径,由此确定剩余点所归属的密度峰值.该方法有效提升了算法执行效率和聚类精度.然而,以上的DPC改进算法分配剩余样本时使用的样本相似度只考虑了样本间的距离,忽略了样本实际分布,仍然会导致某些样本被错误分配.

根据上述分析,本文提出了一种K近邻和加权相似性的密度峰值聚类算法(density peaks clustering algorithm with K-nearest neighbors and weighted similarity,DPC–KWS).DPC–KWS算法的主要创新包括:1)使用样本的K近邻信息重新定义局部密度,它计算的局部密度为样本局部范围内的相对密度,能够调节不同分布类簇中样本的局部密度大小,使得稀疏类簇样本的局部密度升高,密集类簇样本的局部密度降低.新的局部密度定义方式能准确找到疏密程度相差较大数据集中的密度峰值;2) 使用样本的共享最近邻及自然最近邻信息定义样本间的相似性,摒弃了欧氏距离对分配策略的影响,以此确定的样本相似性更符合样本的实际分布,利用该相似性矩阵分配剩余样本,避免了样本分配策略产生的分配错误连带效应,提高了流形数据集的聚类效果.实验表明,本文算法对密度分布不均和流形数据集均能获得满意的聚类结果.

2 DPC算法

DPC算法的基本思想如下:1)密度峰值的局部密度较大,并且被密度均不超过它的邻居包围;2)各密度峰值间的距离相对较远[19].因此,DPC算法提出了局部密度ρi和到最近更高局部密度样本的相对距离δi两个概念.截断核的局部密度计算公式为

其中:dij为样本i与j之间的欧氏距离,dc为截断距离.

当数据集规模较小时,局部密度采用高斯核函数计算,计算公式为

样本i到较高局部密度样本的最近距离由δi表示,δi的计算公式如下:

从式(3)可以看出,如果样本i具有最大的局部密度,则其对应的相对距离也是最大的.

DPC算法将ρi和δi均较大的样本作为密度峰值.为发现密度峰值,DPC算法绘制以ρi为横坐标,δi为纵坐标的决策图来选择密度峰值.为更好地表示密度峰值,DPC算法定义了一个决策值参数γi,即

DPC算法认为局部密度大且距离远的样本为密度峰值,即选择γi值大的点作为密度峰值.找到密度峰值后,剩余的样本被分配给比其密度高的最近样本所在类簇.

3 DPC–KWS算法

由前文的分析得知,DPC算法在局部密度定义和分配策略设计方面存在不足.针对上述不足,DPC–KWS算法从局部密度定义和分配策略设计两方面对DPC算法进行改进.

3.1 K近邻的局部密度

DPC算法的高斯核和截断核的局部密度定义方式均与截断距离相关,且不同数据集的最佳截断距离取值存在较大差异[20];此外,DPC算法的局部密度主要由截断距离范围内的样本决定,截断距离范围外的样本对局部密度的贡献非常低,导致局部密度大的区域内会有更大概率出现密度峰值,对密度分布不均数据而言,就会使类簇中心集中在稠密区域,稀疏区域没有类簇中心.经过分析可知,一个样本与其K个近邻点的相对密度能更真实反映该样本是否为密度峰值.

定义1K近邻的局部密度定义为

这样设计局部密度的优势在于,它使样本的局部密度仅与其K个近邻点有关,排除了远处无关点的干扰,而且它计算的局部密度为该点与其K个近邻点的相对密度,能够调节不同分布类簇中样本的局部密度大小,使得稀疏类簇样本的局部密度升高,密集类簇样本的局部密度降低,更有利于找到稀疏类簇中的密度峰值,从而提高对疏密程度相差较大数据集的聚类效果.

为验证本算法的局部密度定义方式能准确找到疏密程度相差较大数据集的聚类中心.对Jain数据集进行实验,图1为采用高斯核函数计算局部密度得到的类簇中心,图2为采用截断核函数计算局部密度得到的类簇中心,图3为采用K近邻的局部密度得到的类簇中心,图中用“六角星”表示类簇中心.

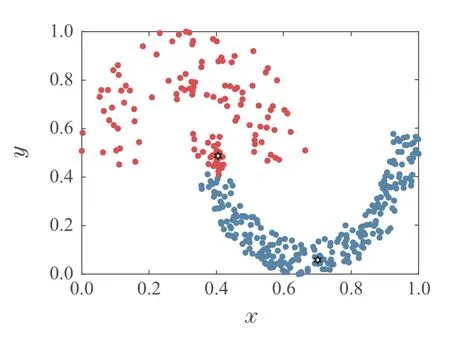
图1 高斯核的局部密度获得的密度峰值Fig.1 The density peaks obtained by the local density of the Gaussian nucleus

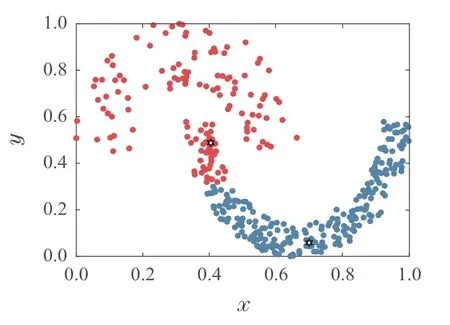
图2 截断核的局部密度获得的密度峰值Fig.2 The density peaks obtained by the local density of the cutoff kernel

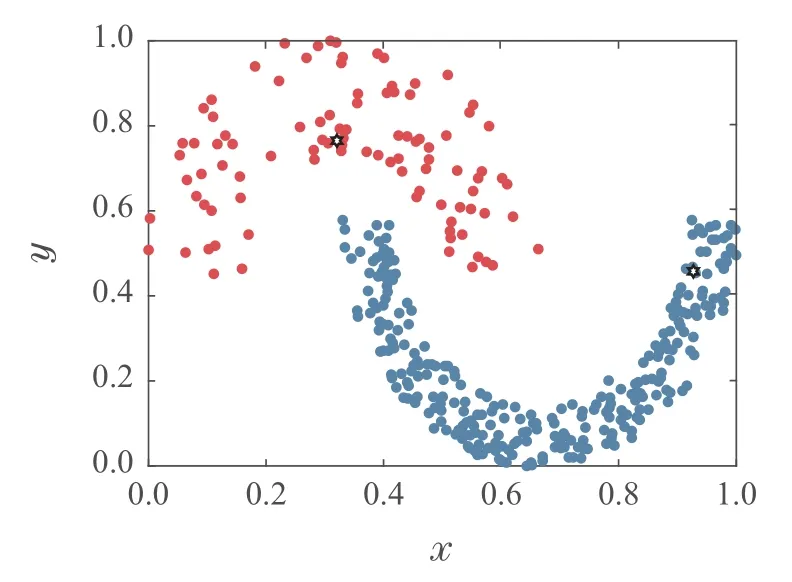
图3 K近邻的局部密度获得的密度峰值Fig.3 The density peaks obtained by the local density of the K-nearest neighbors

从图1和图2可以看出,DPC算法的两种局部密度定义方式没有考虑两类簇的样本疏密程度差异,使得密度峰值均落在密集类簇中,稀疏类簇中没有密度峰值.图3中,K近邻的局部密度定义方法可以准确找到密集和稀疏类簇中的密度峰值.由此可见,K近邻的局部密度定义方式可以增强疏密程度相差较大数据集的密度峰值识别度.

3.2 加权相似性的分配策略

在分配剩余样本时,DPC算法只考虑了样本间密度与距离之间的关系,使得DPC算法虽然能在一些简单的数据集上获得较好的聚类结果,但对于流形数据集,易出现本应属于同一个类簇的样本被错误分配给其他类簇,导致发生分配错误连带效应,致使聚类精度不高.本文采用样本的共享最近邻及自然最近邻信息,重新定义了样本间相似性,该相似性充分考虑了样本所处的局部环境,使样本相似性更符合样本的实际分布,进而避免样本分配错误连带效应.

定义2共享最近邻(shared nearest neighbors,SNN).样本i的K个最近邻样本和样本j的K个最近邻样本的交集称为样本i和j的共享最近邻集合.用公式表示为

定义3自然最近邻(natural nearest neighbors,NNN).如果样本i的K个最近邻样本包含样本j,且样本j的K个最近邻样本包含样本i,则称样本i和j为自然最近邻,取值为1,否则不为自然最近邻,取值为0.用公式表示为

为将剩余样本正确分配,本文设计了一种加权相似性的分配策略:首先依式(8)计算样本i与样本j的相似性ω(i,j),若两点距离越近,则其相似性越高.

其中ω(i,j)为仅从欧氏距离方面度量样本i和j之间的相似性.

仅通过欧氏距离考虑样本间的相似性会忽略样本的周围环境,不能准确反映样本的实际分布,而更准确定义样本间的相似度需考虑样本的共享最近邻和自然最近邻,所以同时使用共享最近邻与自然最近邻对其进行加权处理,这样得到的样本相似性充分考虑了样本所处的环境,避免了样本分配错误连带效应.

Sim(i,j)为考虑样本所处环境时,样本i和j之间的相似性.Sim(i,j)的计算公式如下:

为验证本算法分配策略的优势,采用Pathbased数据集进行实验.图4–5为采用高斯核局部密度定义方式,不同的分配策略得到的聚类结果.图4为采用DPC算法的分配策略获得的聚类结果,图5为采用加权相似性的分配策略得到的聚类结果.

图4 DPC算法的分配策略获得的聚类结果Fig.4 The clustering results obtained by the allocation strategy of DPC algorithm

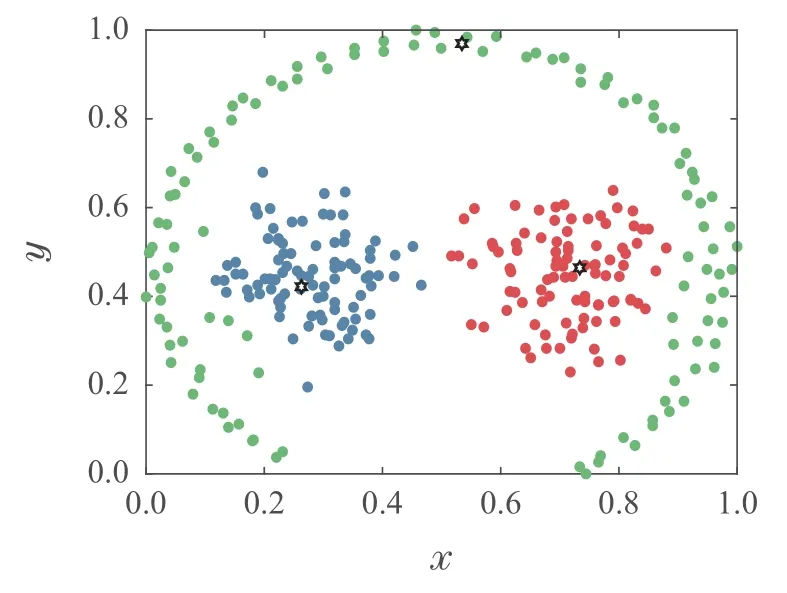
图5 加权相似性的分配策略获得的聚类结果Fig.5 The clustering results obtained by the weighted similarity allocation strategy

从图4可以看出,DPC算法能够准确找到3个密度峰值,但是由于中间两类簇与外围流形类簇中部分样本距离较近,导致分配剩余点产生连带错误,把流形类簇部分样本分配给了中间两类簇.图5中,加权相似性的分配策略能够显著提升外围流形类簇样本的分配准确度,证明了本算法分配策略的有效性.

新的样本分配策略执行流程如下:如式(9)计算样本的加权相似性Sim(i,j);通过样本相似性矩阵寻找与已分配样本相似性最高的未分配样本,并将未分配样本分配给已分配样本所在类簇;循环该操作直至所有剩余样本分配完毕.

3.3 算法步骤

DPC–KWS算法的聚类过程如下:

输入:数据集X={x1,x2,···,xn},样本近邻数K.

输出:聚类结果C={c1,c2,···,cm},m为类簇个数.

步骤1数据预处理,对数据进行归一化处理;

步骤2计算样本间的欧氏距离;

步骤3根据式(5)计算样本的局部密度;

步骤4根据式(3)计算样本的相对距离,根据式(4)计算样本的决策值γi并画出决策图,选取类簇中心集合;

步骤5根据式(8)–(9)计算样本的加权相似性Sim(i,j);

步骤6对所有已分配的样本寻找相似性最高的未分配样本,将未分配样本分配给已分配样本所在类簇,循环该操作直至所有样本分配完毕.

4 实验结果与分析

4.1 实验设置

本实验采用的数据集如表1–2所示.Jain,Pathbased,Lineblob和S2是密度分布不均数据集,其中Jain,Pathbased和Lineblob也是流形数据集;Spiral,Twomoons,Flame和Sticks是流形数据集.它们的样本数量和分布各不相同,用于测试本算法对疏密程度相差较大和流形数据集的聚类效果.8个UCI数据集的样本数量、密度峰值个数和数据维数差异较大,对其进行实验,可测试各算法对问题的普适性.实验部分将DPC–KWS算法与DPC[10],FKNN–DPC[15],DPCSA[21],DPC–DBFN[22]以及IDPC–FA[23]进行比较.所有聚类算法的实验环境均为Intel(R)Core(TM)i5–7300 CPU@2.50 GHz 2.50 GHz,8 GB内存,Windows 10 64bit操作系统和MATLAB 2019b编程环境.

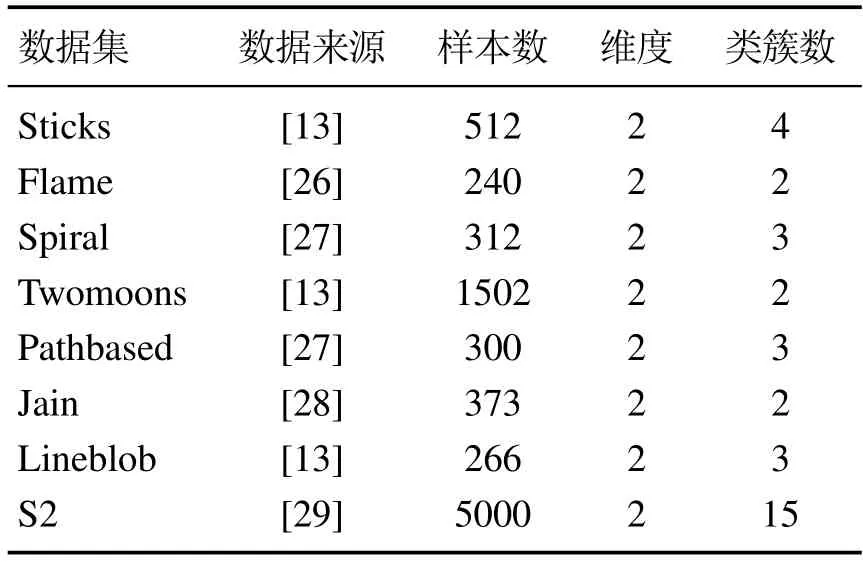
表1 流形及密度分布不均数据集Table 1 Manifold and uneven density datasets

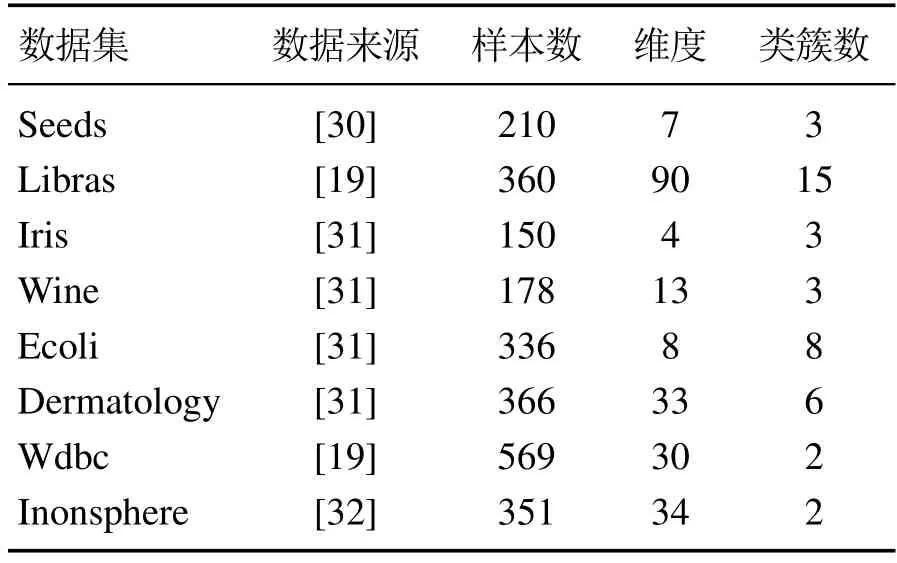
表2 UCI数据集Table 2 UCI datasets

本文选择3个独立于标签绝对值的评价指标评价聚类性能.这些评价指标包括:调整互信息(adjusted mutual information,AMI)[24]、调整兰德系数(adjusted rand index,ARI)[24]和Fowlkes–Mallows指数(Fowlkes–Mallows index,FMI)[25].这3个指标的上限均为1,该值越接近1表示聚类效果越好.本文对比的5种算法中,DPCSA,IDPC–FA,DPC–DBFN和DPC算法代码由原作者提供,FKNN–DPC 算法为参考原文献编程实现.为准确体现各算法性能,本实验对各算法进行参数调优,DPC–KWS,FKNN–DPC和DPC–DB-FN算法需要定义近邻数K,该值在1∼100 之间选取;DPC算法需要设定截断距离,该值在0.01%∼5%之间选取;IDPC–FA和DPCSA 算法无需参数调优,所有实验参数均为对各算法调优后的最优结果.

4.2 流形及密度分布不均数据实验结果分析

表3展示了表1中列出的所有流形及密度分布不均数据在6种算法上的AMI,ARI和FMI指标的聚类结果.表3中的每种算法最好的聚类结果加粗加黑表示,各聚类算法的最优参数用Arg-表示,“–”表示没有对应值.

从表3中可以看出,DPC–KWS算法对8个流形及密度分布不均数据集在每个评价指标上的取值都在0.93以上,表明DPC–KWS算法在流形及密度分布不均数据上均能取得较好的聚类结果.其他对比的聚类算法,均存在对一些数据集的聚类效果不佳.如DPC–DBFN 算法在Spiral 数据集上的效果非常不理想;F-KNN–DPC算法在处理Jain数据集时效果较差;DPC-SA和DPC算法对Jain和Pathbased数据集的聚类效果不理想.

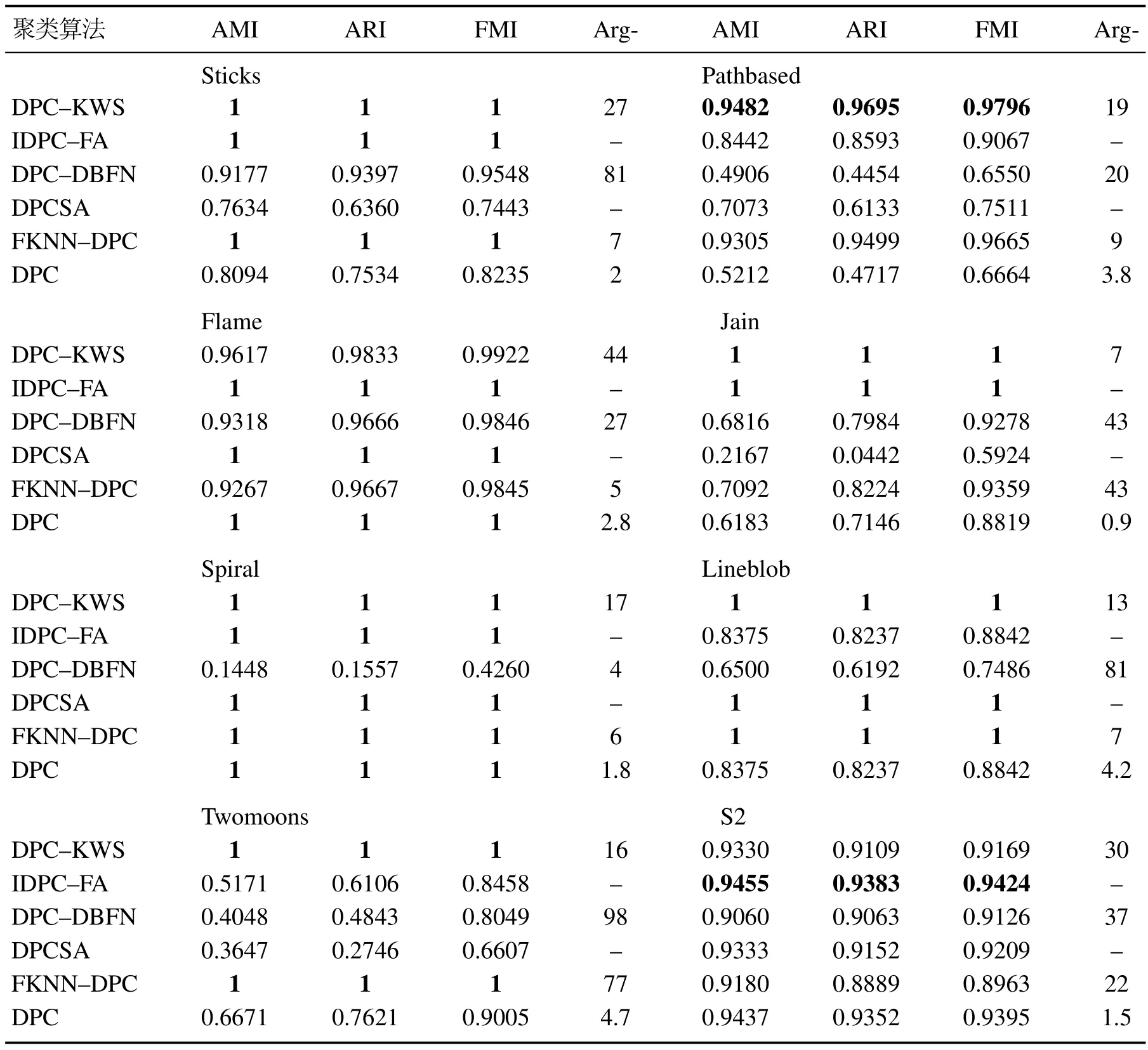
表3 6种聚类算法在8个流形及密度分布不均数据上的聚类性能Table 3 Clustering performance of the six algorithms on eight manifold and uneven density datasets

受论文篇幅所限,图6–7仅展示各聚类算法对Pathbased和Jain数据集的聚类结果.图中不同颜色的点代表不同的类簇,“六角星”表示密度峰值.

图6为6种算法对Path-based数据集的聚类结果.Pathbased数据集一共有300个样本,包含两个团状类簇和一个流形类簇,其中流形类簇包围了两个团状类簇,由于3个类簇之间联系紧密,样本的分配很容易发生连带错误.对该数据集,DPC–KWS和FKNN–DPC算法聚类效果明显优于其余算法,仅个别边缘样本被分配错误.其余算法均能正确找到密度峰值,但是由于团状类簇与流形类簇中部分样本距离较近,致使分配剩余点产生连带错误,所以聚类效果不理想.

图6 6种聚类算法对Pathbased数据集的聚类结果Fig.6 Clustering results of six algorithms on Pathbased dataset

图7为6种算法对Jain数据集的聚类结果.该数据集由两个月牙状类簇组成,上面的类簇较为稀疏,下面的类簇较为密集,是典型的疏密程度不一的流形数据集.对该数据集,6种算法中IDPC–FA和DPC–KWS算法能够准确聚类,DPC和DPCSA算法没有准确找到密度峰值,两个密度峰值均在密集类簇中,使得分配剩余点发生连带错误.其余算法虽然能够准确找到密度峰值,但错误地把密集类簇中较多的样本分配给稀疏类簇,使得聚类效果较差.

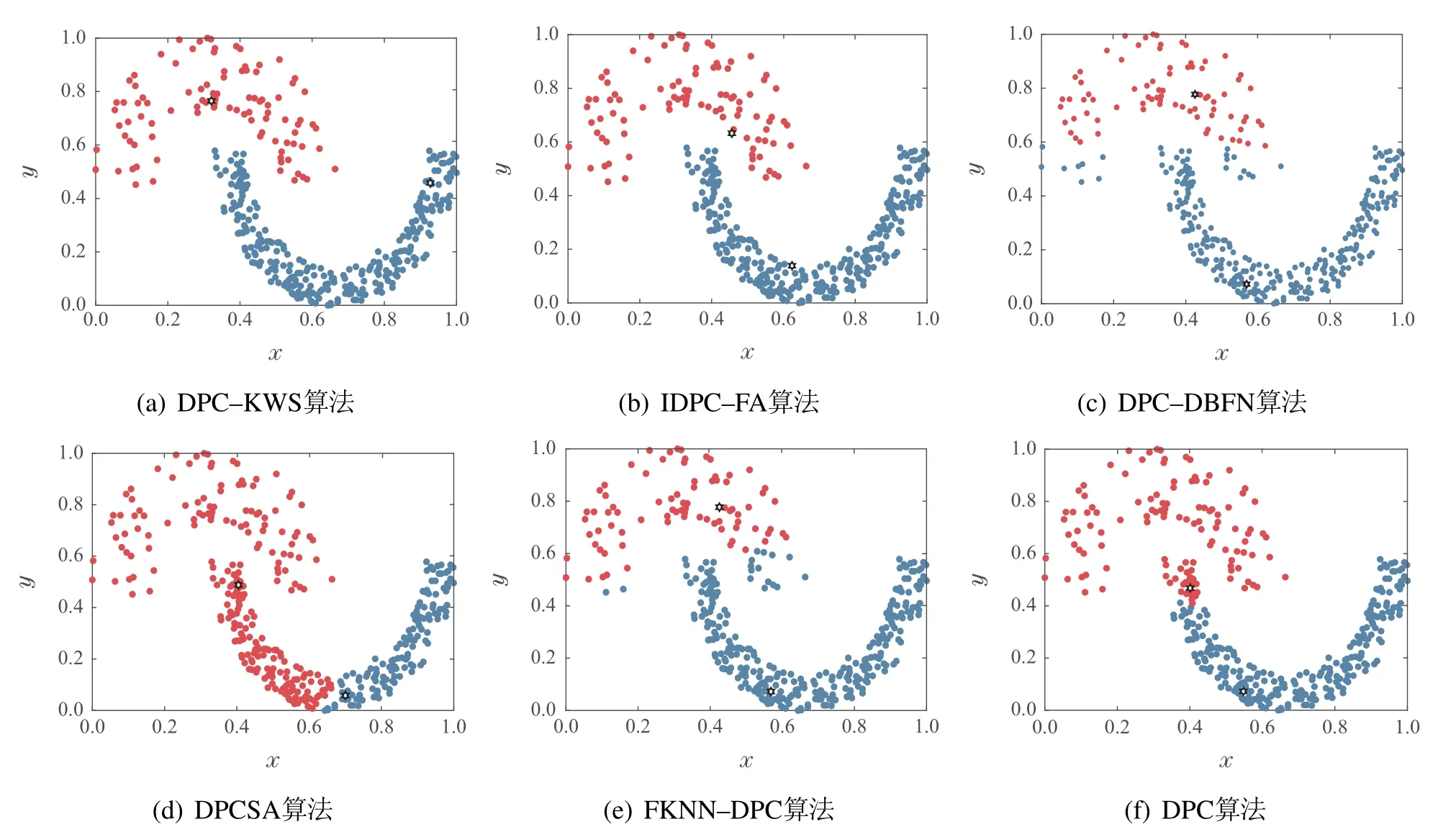
图7 6种聚类算法对Jain数据集的聚类结果Fig.7 Clustering results of six algorithms on Jain dataset

4.3 真实数据集实验结果分析

为进一步验证DPC–KWS算法的有效性,将6种聚类算法在8个真实数据集上进行实验.表4给出了8个真实数据集在AMI,ARI和FMI指标的聚类结果.从表4可以看出,DPC–KWS算法整体性能最优,在Seeds数据集上,DPC–KWS算法的聚类效果不如FKNN–DPC算法;在Dermatology数据集上,DPC–KWS算法的聚类效果不如IDPC–FA算法;在Iris数据集上DPC–KWS聚类效果与FKNN–DPC和DPC-SA聚类效果相同;剩余的Ecoli,Libras,Wdbc,Wine 和Inonsphere数据集上,聚类性能最好的算法均为DPC–KWS算法.

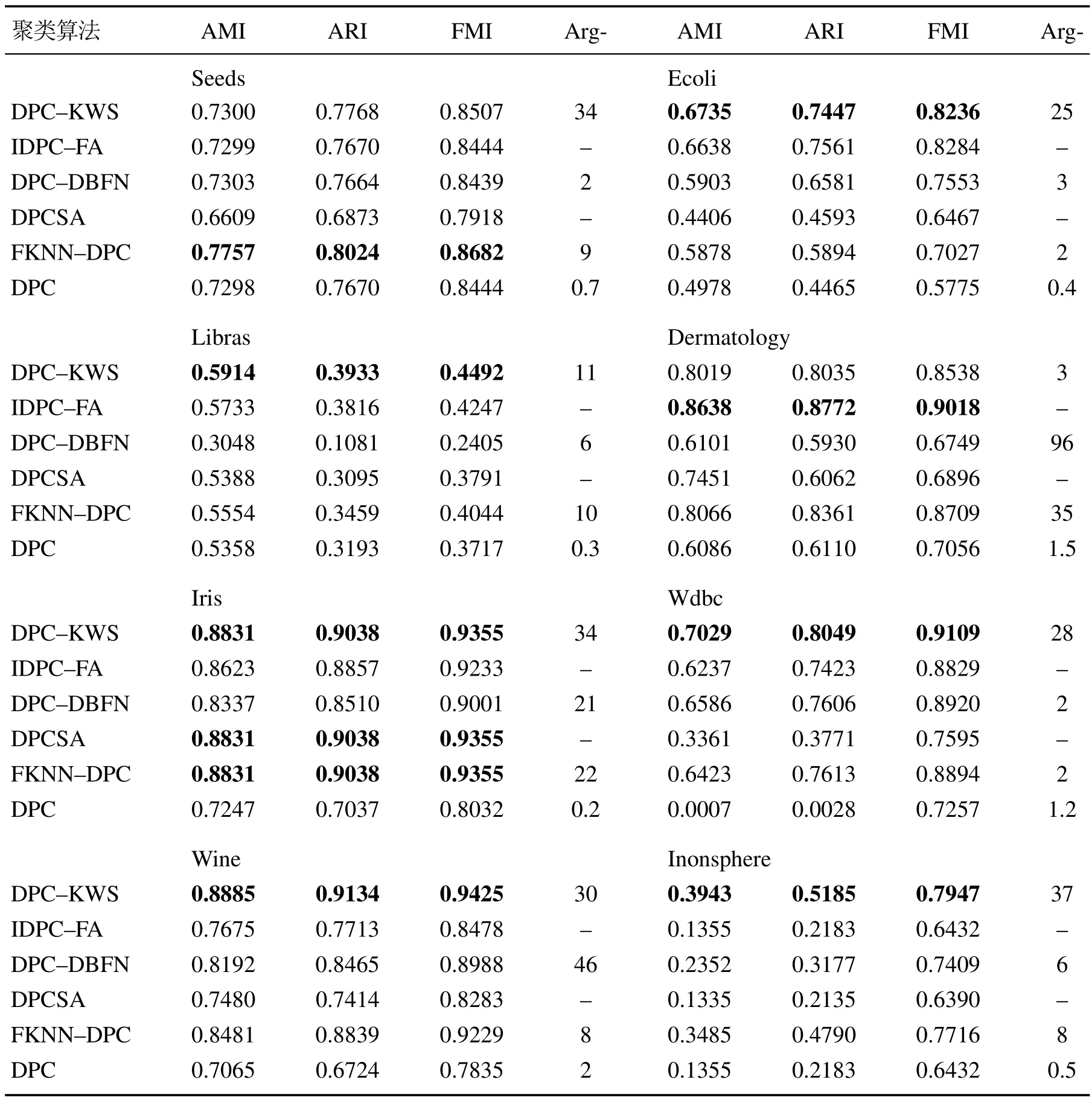
表4 6种聚类算法在8个UCI数据集上的聚类性能Table 4 Clustering performance of the six algorithms on eight UCI datasets

5 总结

针对DPC算法聚类密度分布不均数据集易误选类簇中心和流形数据集易错误分配样本的问题,本文提出了一种K近邻和加权相似性的密度峰值聚类算法.DPC–KWS算法使用样本的K近邻信息重新定义了样本的局部密度,新的局部密度为样本局部范围内的相对密度,能准确找到密度分布不均数据中的密度峰值;使用共享最近邻及自然最近邻定义样本间的相似性,摒弃了欧氏距离对分配策略的影响,新的样本相似性更加符合样本的实际分布,利用该相似性矩阵分配剩余样本,避免了样本分配策略产生的错误连带效应,提高了流形数据的聚类效果.实验结果表明,本文算法对密度分布不均和流形数据集均能得到满意的聚类结果.如何自动确定算法的最佳参数K与提高算法在高维数据集上的聚类效果将是下一步的研究重点.