EEG信号识别中可调优化Q因子小波变换的多特征融合算法

刘 朕,朱炳宇,张景祥

(江南大学理学院,江苏无锡 214122)

1 引言

在脑部疾病诊断中,脑–机接口(brain-computer interface,BCI)利用外部设备采集脑电信号(electroencephalogram,EEG),实现了脑电信号与外界的交互[1].运动想象脑电信号是大脑受到外界运动想象刺激生成,当大脑受到单侧肢体的运动想象的刺激时,其对侧运动感知区则处于激活状态,与其对应节律的幅值会降低,这种现象称为事件相关去同步(event-related desynchronization,ERD).大脑同侧的感知区则处于抑制状态,对应节律的幅值则会升高,这种现象称为事件相关同步(event-related synchronization,ERS).利用运动想象特定频段中存在的ERD/ERS现象,可以实现对运动想象脑电信号的有效识别[2].考虑到ERD/ERS的特定频域特征空间下的信息可能有助于运动想象信号识别,本文对ERD/ERS对应的频域区间信号提取特征.

EEG信号随时间变化具有非线性、非平稳特征,且不具备各态历经性[2].现有的EEG信号识别方法大致分为3类:时域分析法、频域分析法和时频分析法.时域分析方法是将EEG信号作为时序数据,分析信号内部的时域特征.时域分析方法代表性的工作有:Ghosh-Dastidar等人[3]利用主成分分析(principle component analysis,PCA)提取EEG信号的时域特征,度量不同EEG信号类别之间的时域差异性.Ozcan等[4]对EEG信号提取谱宽度,统计矩以及Hjorth等统计特征,结合深度学习实现癫痫EEG信号的自动诊断.频域分析方法则将信号映射到频域中,分析不同频率子空间上信号存在的差异.频域分析方法代表性的工作有:Zhang等人[5]利用稀疏化贝叶斯学习算法,分析EEG的不同频率区间,结合稀疏化贝叶斯学习选择重要的特征,完成运动想象信号的识别.Mehla等人[6]使用了傅里叶分解的方法,将EEG信号分解成傅里叶本征带函数进行特征提取,提高了癫痫信号的识别率.时频分析方法结合时域和频域对EEG信号处理.时频分析方法代表性的工作有:王洪涛等[7]选择不同的时间窗和频带,通过多个共空滤波器提取时频特征,结合相关向量机实现运动想象信号识别.Acharya等人[8]利用样本熵,相位熵和近似熵分别对EEG信号进行处理,多尺度的分析了信号的时频信息,对信号中的癫痫特征进行检测.Fu等人[9]提出稀疏化共空间模式的正则判别分析算法,对运动想象EEG信号进行识别.孟明等[10]将通道间的差异性与共空间模式结合,根据时频信息的Fisher比划分块的分类能力,提出块选择共空间模式算法识别运动想象信号.陈万忠等[11]针对运动想象EEG信号模式精度以及互信息不高的问题,结合多尺度特征提出基于可调Q因子小波变换的EEG信号识别算法.Al Ghayab等[12]将运动想象EEG信号进行TQWT分解,分别提取不同小波子带的统计学特征,结合机器学习算法完成识别.

上述方法在运动想象EEG信号识别上虽然取得一定的效果,但仍存在一些不足之处:

1)时域和频域的方法仅分析了信号在各自域的特征,其他维度信息缺失,导致识别精度较差;

2)时频分析中,在可调Q因子小波变换方法的应用中,存在小波变换参数难以确定的问题,且特征存在冗余.

针对上述问题,本文基于可调Q因子小波变换(tunableQ-factor wavelet transform,TQWT)以及特征选择的理论,提出一种基于可调优化Q因子小波变换的多特征融合的EEG信号识别算法(adaptive-tunableQfactor wavelet transform multi-feature,Ad-TQWT MF).Ad-TQWT MF算法利用能量香农熵比的指标,确定TQWT中最优的Q因子,并结合EEG信号的时域,频域和非线性多维特征,自适应特征选择,对特征提取后的数据进行稀疏化处理,减少冗余特征,降低数据维度以及计算复杂度,减少模型训练的时间.本文将能量香农熵比(energy-shannon entropy ratio,ESER)作为TQWT中Q因子的优化评价标准,选择合适的Q因子,提高TQWT对EEG中运动想象的识别能力,并结合样本熵,LP系数,小波能量以及分形维数,多维度提取EEG中运动想象信息,最后自适应特征选择确定最优特征子空间进行EEG信号识别.本文方法的特色之处在于:

1)对不同Q因子下TQWT分解后得到的子带,分别计算其子带能量和香农熵,能量与香农熵的比值作为评价该小波分解的优劣指标,使小波匹配EEG运动想象的震荡特性;

2)在小波子带的特征提取中,嵌入样本熵,LP系数等时域特征,以及小波能量,分形维数等频域非线性特征,充分提取了EEG不同维度下的信息;

3)针对多维特征存在的冗余问题,利用自适应特征选择确定最优特征子空间,降低了模型复杂度,提高了EEG信号识别精度.

2 可调优化Q因子小波的多特征融合(Ad-TQWT MF)

由于EEG信号的非线性和非平稳性存在难以识别的波段,合适的小波可提取EEG的特殊频段[2].利用小波基函数将信号分解为不同频率的子带,传统的小波基有Haar,Db_4等.但这些小波均为恒定Q因子小波,无法与EEG信号中震荡成分相匹配.TQWT可调节不同的Q因子,适应信号非平稳的特性,充分地保留原信号震荡信息.但TQWT在Q因子的选择上依赖数据先验信息或特定实验,在理论上缺乏评判指标[10–11].针对这个问题,本文根据信号分解的最大化能量以及最小化香农熵准则,提出了Ad-TQWT MF算法.能量香农熵比优化TQWT的Q因子,使小波更准确提取信号中存在的ERD/ERS特征,并融合多维度特征,选择最佳特征子空间,通过分类器完成对EEG信号的识别.Ad-TQWT MF算法的总体流程如图1所示.

图1 Ad-TQWT MF算法流程图Fig.1 Flow chart of Ad-TQWT MF

2.1 可调Q因子小波变换(TQWT)

TQWT与普通小波变换处理信号的过程类似[13],该分解中小波的Q因子影响其对信号信息的提取能力,不同Q因子的小波能分解出对应频率成分,TQWT通过调节Q因子使得小波与原信号中震荡成分相匹配,提取信号中的震荡信息.

信号X(n)的TQWT分解中,利用两个滤波器组H0(ω)和H1(ω)进行滤波后,再进行尺度缩放,实现低频与高频信号的分离.H0(ω)和H1(ω)称为低通和高通滤波器,其具体形式如式(1)–(2):

其中α,β分别为低通和高通缩放尺度参数,它们的大小决定了滤波器组H0(ω)和H1(ω)保留信号X(n)的区间大小,影响TQWT对信号波动的分解提取能力.根据文献[13]中指出小波变换应满足对信号分解重构的条件,因此α,β需满足式(3)的约束条件

式(1)–(2)中H0(ω)与H1(ω)相交的区间称为过渡带,即ω∈[−απ,−(1−β)π]∪[(1−β)π,απ].对于过渡带的信号,滤波函数采用具有二阶消失矩的Daubechies频率响应θ(ω),函数的具体形式以及性质如式(4):

结合式(1)–(2)(4),可知过渡带上滤波函数满足式(5),

结合式(3)尺度参数α,β的约束条件以及式(5)H0(ω)和H1(ω)性质,TQWT符合小波重构的原理,可以实现信号分解以及重构.

TQWT信号分解中存在两个重要的参数Q因子以及冗余率r.其中,Q因子是衡量小波提取X(n)震荡特性的一个重要指标,它定义为小波中心频率ωc与带宽BW的比值,与尺度参数β相关,具体定义如式(6):

冗余率r由尺度参数α,β定义,具体形式如式(7):

上述式(6)–(7)中,Q因子,冗余率r均与TQWT中α,β相关,由于实际采集的均为有限长度信号,故实际信号的TQWT分解存在上限.文献[13]给出了有限时长的信号最大分解层数Jmax,定义如式(8)所示:

其中⎿∗」为向下取整函数.从式(8)最大分解层数Jmax的定义可知,调整尺度参数(α,β)的大小,其TQWT对信号的分解层数会随之变化.式(6)–(7)揭示了(Q,r)的大小与尺度参数(α,β)之间的联系.EEG信号经过TQWT分解后得到各个子带系数,其中第i层低频系数li(ω)如式(9)所示:

其中f(x,ω)=x(n)e−jnαiω.同理,可得第i层的高频系数hi(ω)如式(10)所示:

其中:θ0(ω),θ1(ω)满足式(4)的滤波函数的条件,即

区间范围中

2.2 可调优化Q因子小波(Ad-TQWT)

从上述信号TQWT分解中,Q因子影响式(1)–(2)的H0(ω)和H1(ω)滤波范围以及分解层数,因此合适的Q因子是提取EEG运动想象相关信息的关键.现有Q因子的选择过分依赖实验结果以及先验信息,但这些信息获取难度较大,不利于Q因子的选择.本文提出使用能量香农熵比(E-SER)[14]评价不同Q因子下TQWT对EEG信号的分解效果,最大化TQWT分解EEG信号后子带保留的特征信息.

图2 Ad-TQWT的J层分解与Q因子优化Fig.2 Decomposition-J and Q-factor optimization of Ad-TQWT

TQWT分解得到的各子带可分别计算其E-SER指标,该指标主要通过信号的能量和香农熵进行定义.对于分解得到的第i个低频子带li(n),利用式(11)可计算其能量Ei0,即

式(13)–(14)中,各区间离散化后离散点总数满足条件

增多.n2对应的频率区间将会变窄,其项数减少.由此,Q因子的增大会引起高频子带中的过渡频率变高,低频段区间变窄,分解后的能量也会发生相应的变化,因此可以得到信号分解的最大能量准则.

最大能量准则[14]:小波分解后子带的能量越大,小波与原信号的匹配度越高,小波分解后保留的信息越充分.

最小香农熵准则[14]:香农熵的大小反映出其系数的分布情况.香农熵越低,说明该系数分布的不确定性越低,小波分解后得到的信息就越多.

图3 S4b数据集不同Q因子的¯RFig.3 ¯R of different Q-factor in S4b

2.3 EEG信号多维度特征融合

为进一步提取EEG信号的信息,需对原始EEG信号和分解得到的子带进行特征提取.文献[11]中主要提取多维度特征,但忽略了信号自身波动之间的差异性,这在检测运动想象中尤为重要.因此,本文此基础上嵌入样本熵特征,挖掘EEG信号自身波动信息.

2.3.1 EEG信号的时域特征

样本熵[15](sample entropy,SampEn)计算序列中相同波动的概率,度量序列的复杂程度,反映EEG信号随时间推移产生的差异性.样本熵越大,序列复杂度越高,EEG信号存在不同波动的可能性越大.反之样本熵越小,其复杂度越低[16].

对于EEG序列X={x1,x2,···,xN},定义m维向量序列Xm(i)={xi+1,xi+2,···,xi+m−1},原序列X的样本熵通过计算不同时段数据的差异,利用其比值度量波动大小,样本熵具体定义如下式(19):

式中:N为EEG信号序列总长度,m为时间间隔,一般取为2,t为判断距离的阈值,取值范围为[0.1Std(X),0.35Std(X)],Std(X)是原始序列X的标准差.式(20)中的Ai和Bi按式(21)定义,

其中:j∈[1,N −m],card(∗)函数是统计集合元素个数,Ai和Bi分别表示序列长度为m和m+1时存在差异的元素个数.序列Xm(i)与Xm(j)的差异大小可通过切比雪夫距离定义序列距离,即二者对应向量元素差的无穷范数.具体定义如式(22):

其中∥∗∥∞为向量的无穷范数.式(22)利用切比雪夫距离衡量序列Xm(i),Xm(j)之间距离,通过两个序列对应的最大差值,可以有效地反映出两者之间存在差异的上界,提高SampEn特征的可区分性.

以S4b数据集为例,对该数据集的训练集的两个通道数据计算相应左右手样本熵的值,如图4所示.

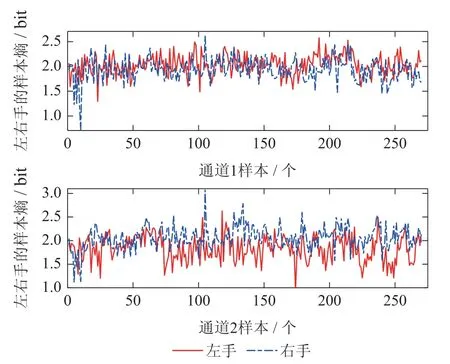
图4 S4b数据集左右手样本熵Fig.4 SampEn of left-right sample in S4b

图4中,实线代表左手样本的样本熵,虚线代表右手样本的样本熵.从通道1的图中可以看出,左手的样本熵略大于右手,通道2中左手样本熵均位于右手的下方,说明该通道左手与右手运动想象EEG的样本熵存在明显差异.样本熵的差异有效佐证了该特征在分类左右手EEG信号的有效性.

线性预测(linear predication,LP)[17]是分析时序数据的一种模型,模型系数刻画了t时刻信号强度与t −i时刻之间的关系,具体定义如下:

其中:x(t),x(t−i)分别为t和t−i时刻EEG信号强度,l为与t时刻相关的时刻点数,ai为模型的LP系数.ai越大,说明t与t −i时刻的相关性越大.反之,t −i对t时刻的影响越小.利用式(19)(23)定义的样本熵和LP模型,分别计算EEG信号的样本熵和LP系数,将其作为EEG信号的时域特征.

2.3.2 EEG信号的频域和非线性特征

TQWT对EEG信号进行J层分解后,信号被分解成J+1个不同频率的子带,对应各频率的分量.因此子带能量分布反映各个频率区间上EEG的能量分布情况[18],经TQWT分解后的能量E是式(11)(13)定义的所有低、高频子带能量(Ei0,Ei1)的集合,即

分形维数是通过定义分形,度量EEG信号中局部与整体的相似性,具有自相关性与标度不变性[19].其中计盒维数的分形d(s)具体定义如下:

其中:G为每一个网格的长度;Nn(s)表示在长度为Gl的网格中覆盖分形s所需的最小网格数;d(s)是一种非线性特征,d(s)越大,序列的复杂度越高[20].根据式(24)–(25)定义的小波能量以及分形维数,分别计算EEG信号的分形维数和小波能量,作为其频域和非线性特征.

2.3.3 EEG信号特征融合和选择

对时,频和非线性特征提取时,特征空间之间可能存在重叠,出现特征冗余.特征选择(feature selection,FS)在确保不丢失重要特征的前提下,根据实际任务目标对评估特征,去掉冗余特征[21],本文在过滤式特征选择的基础上提出自适应特征选择算法,将分类精度融入特征评价中,加强特征与分类器之间的联系,自适应地完成特征选择.算法1给出了EEG信号的Ad-TQWT MF算法的具体流程.

3 实验分析

为了验证Ad-TQWT MF算法的可行性、有效性以及鲁棒性,本节利用该算法对BCI竞赛数据集进行实验.选用第二,三届BCI竞赛的EEG左右手数据集,其中Dataset_III以128 Hz对C3,Cz和C4三个通道进行采样,每次采集9 s时长的信号,O3VR,X1b和S4b均以125 Hz对C3和C4两个通道进行采样,每个实验时长为8 s,4个数据集的信号均经过Notch滤波器处理后,频率在ERD/ERS可能存在的0.5 Hz和30 Hz区间内.实验前去除数据中异常样本,在进行特征提取之前,为满足数据平稳性的要求还需对数据进行窗口化处理[22].数据集中样本的具体信息如表1所示.

表1中,Dataset III采用时长为3 s的滑动窗口,从t=6 s开始并以∆t=0.125 s滑动,其余3个数据集均采用时长为4 s的滑动窗口,从t=4 s开始并以∆t=0.04 s滑动,表1中最后一列为窗口化后数据集的样本数.

表1 实验数据集Table 1 Experiment Dataset

3.1 特征提取

根据TQWT的分解重构原理以及采样频率,结合ERD/ERS现象存在的频率区间和文献[23]的先验信息,可以确定Dataset_III的Q因子取值范围为[1,12],其余3个数据集的Q因子取值范围为[1,10].对于上述4个数据集,分别对各区间寻优后确定适合其数据集的Q因子,各数据集优化前后各参数见表2.

表2 数据集TQWT分解参数Table 2 Parameters of TQWT in different datasets

根据表2中优化后的Q因子,冗余率r和分解层数J分别对各数据集进行TQWT分解.根据式(9)–(10)计算各子带系数,按式(11)(13)小波能量特征.利用式(25)计算分形维数,分形网格的分割上限取为2048,将这两个维度作为频域特征.除频域特征外,还需提取样本熵和LP系数等时域特征,按式(19)计算各数据集样本熵,最后通过式(23)建立LP模型,数据集1和4的LP系数l为8,数据集2和3的LP系数l为8.

3.2 特征选择

通过样本熵,LP系数,小波能量以及分形维数对各数据集进行特征提取,得到样本的特征维数见表3.利用Ad-TQWT MF的自适应特征选择算法提取特征子空间,得到去除的样本特征维度序号如表4所示.其中X11b数据集减少了28%的特征,其他3个数据集删除的特征比例范围在10%∼18%之间.经过自适应特征选择对特征进行筛选后,去除了原数据集中冗余特征,降低了训练数据的规模和模型复杂度.

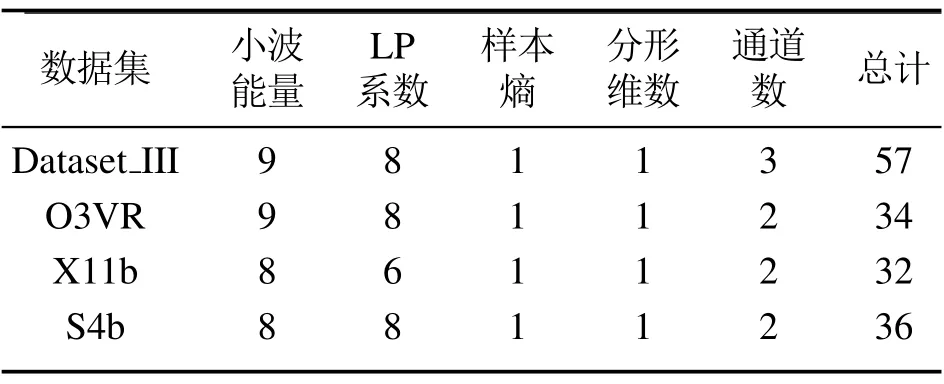
表3 样本的特征维度Table 3 Feature dimensions of the sample

表4 特征选择去除的特征维度Table 4 Feature dimensions removed by feature selection

3.3 分类性能比较

经过特征提取以及特征选择后,将最终得到的特征集依次放入线性判别分类器(linear discriminant analysis,LDA),支持向量机(support vector machine,SVM)以及高斯核支持向量机(高斯SVM)中进行训练.为说明Ad-TQWT MF算法的可行性和有效性,还将Haar以及Db_4小波函数处理得到的数据集作为对照组.对上述数据集进行特征提取和分类时采用了十折交叉验证,将测试集准确率的均值作为最终算法的分类准确率.以X11b数据集为例,分别利用5种不同特征提取方法(Haar,Db_4,TQWT,Ad-TQWT,Ad-TQWT MF)进行特征提取,分别放入LDA,SVM以及高斯SVM进行训练,得到各方法的ROC曲线.其中,Haar小波结合3个分类器的ROC曲线如图5所示,从图5中看出Haar小波在3个分类器的AUC均为88%,模型的测试准确率分别为81%,81%和78%.Haar小波是最常见的二进制小波,其小波具有离散不连续性,导致其不能充分提取左右手波动特征,因此信号分类的精度较低.

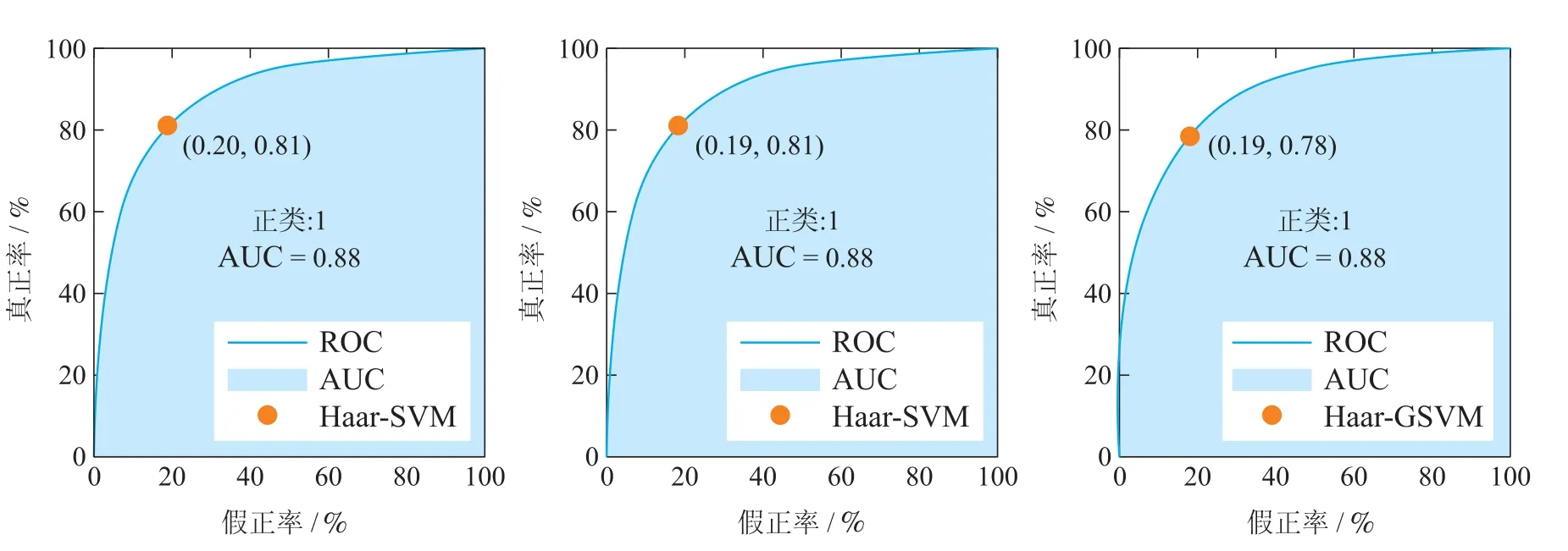
图5 Haar的ROC曲线(X11b-LDA,SVM,高斯SVM)Fig.5 ROC of Haar(LDA,SVM and GSVM in X11b)

Db_4小波作为一种连续小波,解决了Haar小波不连续的问题.图6给出了该小波提取特征后3个分类器的ROC曲线,从图6中,可以看出Db_4小波提取的特征集合,经过3个分类器分类的AUC均为88%,模型的测试准确率分别为81%,82%和79%.较于Haar小波,Db_4小波函数具备连续性,提取EEG左右手特征的能力上有所提高,但由于其Q因子固定不变,该小波不能适应EEG信号非平稳的波动特性.

图6 Db_4的ROC曲线(X11b-LDA, SVM, 高斯SVMFig.6 ROC of Db_4(LDA, SVM and GSVM in X11b

TQWT与Haar,Db_4小波不同,其Q因子可调节,图7是TQWT提取特征训练后的ROC曲线.图7中,可以看出TQWT提取的特征集合经过3个分类器的AUC分别为88%,88%和89%,模型的测试准确率分别为80%,82%和79%.较于Haar和Db_4小波,TQWT其Q因子可根据信号的特性进行调节,可以适应EEG信号中复杂震荡的情况,但在实际的Q因子选择中,需大量的实验缺乏理论方法.

图7 TQWT的ROC曲线(X11b-LDA,SVM,高斯SVM)Fig.7 ROC of TQWT(LDA,SVM and GSVM in X11b)

针对Q因子选择缺乏理论的问题,利用E-SER评价Q因子,Ad-TQWT分解信号得到的ROC曲线如图8,Ad-TQWT在3个分类器AUC均为90%,模型的准确率分别为84%,84%和82%.较于原TQWT,Ad-TQWT其Q因子优化后,小波更准确匹配EEG 信号中特定震荡,使信号提取的特征信息更加充分.

图8 Ad-TQWT的ROC曲线(X11b-LDA,SVM,高斯SVM)Fig.8 ROC of Ad-TQWT(LDA,SVM and GSVM in X11b)

Ad-TQWT虽然提取了多维度特征,但忽略了特征之间的相关性,可能出现特征冗余,因此利用特征选择合适的特征子空间,提出Ad-TQWT MF算法.其分类的ROC曲线如图9.

图9中3个分类器的AUC均为90%,其测试的准确率分别为85%,84%和82%.较于前面4种方法,本文提出的Ad-TQWT MF算法,充分提取EEG信息,利用自适应特征选择合适的特征子空间,降低了模型复杂度,提高了模型的准确率,佐证算法的可行性以及有效性.

图9 Ad-TQWT MF的ROC曲线(X11b-LDA,SVM,高斯SVM)Fig.9 ROC of Ad-TQWT MF(LDA,SVM and GSVM in X11b)

表5给出了所有训练数据集在3个分类器下具体的测试准确率以及AUC,从表5的实验结果分析,可以得到如下的结论：

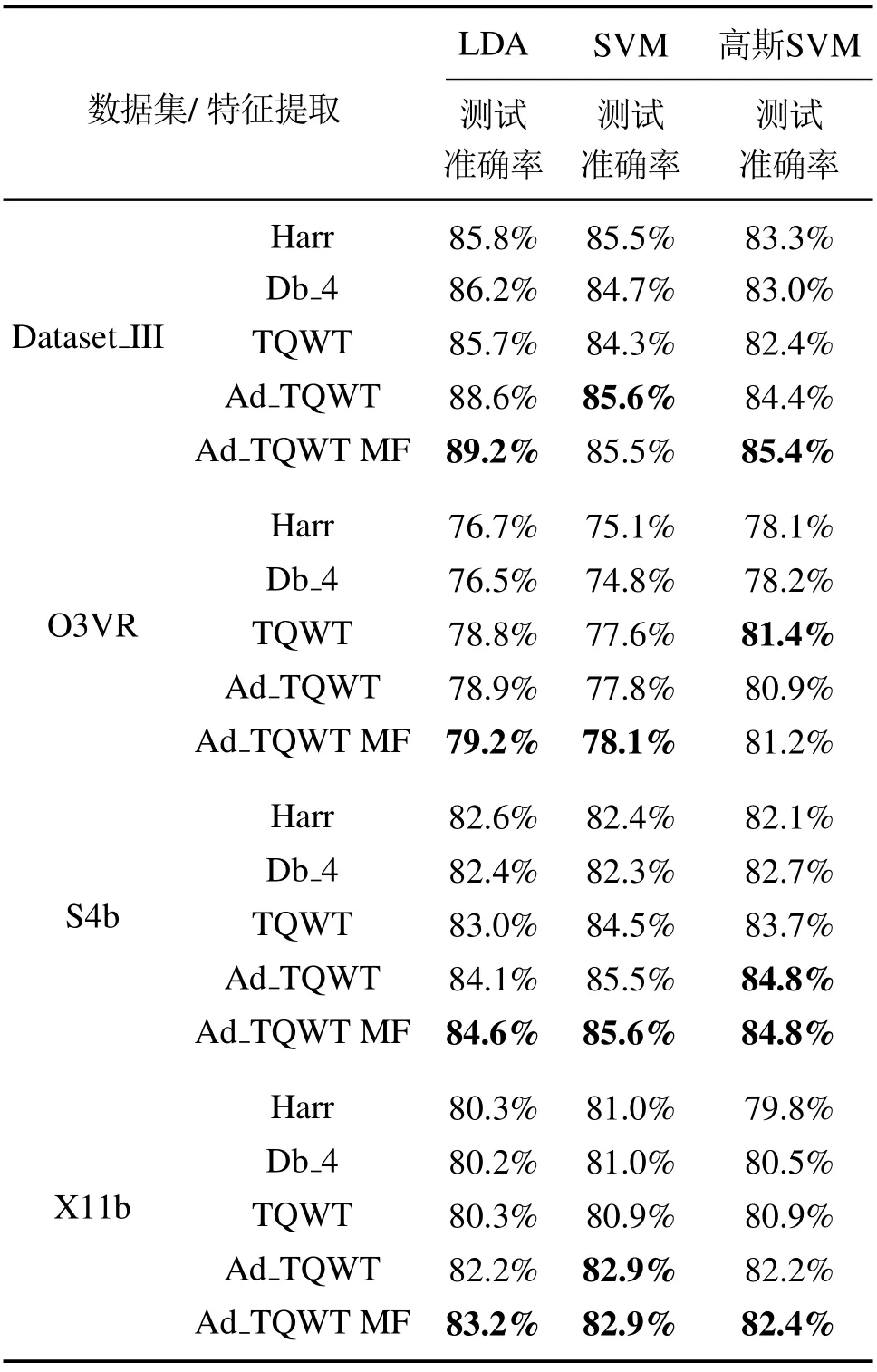
表5 各数据集的测试准确率Table 5 Test accuracy of each dataset

1)Ad-TQWT与Haar,Dd_4小波和TQWT相比,对O3VR和S4b的识别中测试准确率提高了1%∼3%,在Dataset_III和X11b中提高了2%∼4%;

2)在TQWT与Ad-TQWT MF算法识别EEG信号中,后者利用能量香农熵比作为Q因子评价指标,融合时域,频域和非线性特征,通过自适应特征选择构建特征子空间,去除了10%∼30%冗余特征,提高了2%∼5%准确率;

3)在LDA,SVM以及高斯SVM 3种分类器中,Dataset_III和X11b在LDA下测试准确率比SVM与高斯SVM高1%∼4%.O3VR在高斯SVM的测试准确率高出LDA和SVM2%∼3%.S4b在SVM下测试准确率最高达85.6%Ad-TQWT MF算法在不同分类器上识别的测试准确率均为最高.针对不同的数据集,Ad-TQWT MF均可进一步提高识别EEG信号的精度.

4 展望

本文针对EEG信号识别中TQWT参数Q因子无优化评价标准,特征存在冗余的问题,提出Ad-TQWT MF算法.通过能量香农熵比作为TQWT的Q因子优化评价标准,选择最优Q因子小波变换,将时,频域和非线性特征融合,自适应的特征选择获取特征子空间,提高了EEG信号的识别精度.后续工作将在EEG信号的异常特征提取方面进一步开展相关研究.