不定方程Kx(x+1)(x+2)(x+3)= Dy(y+1)(y+2)(y+3)(x>0,y>0)的解
杨雅琴
(齐齐哈尔大学 理学院,黑龙江 齐齐哈尔 161006)
设K、D是互素的非负整数,且K
设K、D、M是已知的非负整数,K、D互素且K 定理1对不定方程x2-Dy2=M2,设D=ab(0≤a 证明设D=ab(0≤a≤b≤D),x>0,y>0,不定方程x2-Dy2=M2可变形为x2-M2=Dy2,有: x2-M2=(x-M)(x+M)=Dy2=aby2≥0, 则x-M与x+M同号. 因a≤b,所以下面考虑3种情况:a|(x-M),b|(x+M);ab|(x-M);ab|(x+M). (2)当ab|(x-M)时,存在p∈Z,使得x-M=abp=Dp,x+M=Dp+2M.由 x2-M2=(x-M)(x+M)=Dy2, (3)当ab|(x+M)时,由于x≥M≥0,则存在q∈Z,使得x+M=abq=Dq,x-M=Dq-2M≥0.由 x2-M2=(x-M)(x+M)=Dy2, 例1求不定方程x2-42y2=12的解. 解因D=42=1×42=2×21=3×14=6×7,M=1. 是不定方程x2-42y2=12的解,有3372-42×522=12. 是不定方程x2-42y2=12的解. 是不定方程x2-42y2=12的解,有132-42×22=12. 是不定方程x2-42y2=12的解. (2)因D=42,取p=8,使得p(Dp+2M)=8×(42×8+2×1)=522是平方数.则 是不定方程x2-42y2=12的解. (3)因D=42,取q=-8,使得q(Dq-2M)=(-8)×[42×(-8)-2×1]=522是平方数.则 是不定方程x2-42y2=12的解. 例2求不定方程x2-34y2=332的解. 解因D=34=1×34=2×17. 是不定方程x2-34y2=332的解,有352-34×22=332. 是不定方程x2-34y2=332的解,有8172-34×1402=332. (2)因D=34,取p=1,使得p(Dp+2M)=1×(34×1+2×33)=100是平方数.则 是不定方程x2-34y2=332的解,有672-34×102=332. 取p=8,使得p(Dp+2M)=8×(34×8+2×33)=522.则 是不定方程x2-34y2=332的解,有3052-34×522=332. 取p=33,使得p(Dp+2M)=33×(34×33+2×33)=1982,则 是不定方程x2-34y2=332的解,有1 1552-34×1982=332. 取p=128,使得p(Dp+2M)=128×(34×128+2×33)=7522.则 是不定方程x2-34y2=332的解,有4 3852-34×7522=332. (3)因D=34,取q=49,使得q(Dq-2M)=49×(34×49-2×33)=2802.则 是不定方程x2-34y2=332的解,有1 6332-34×2802=332. 引理4个连续非负整数的乘积加1是平方数. 证明对任意非负整数n,有: n(n+1)(n+2)(n+3)=n(n+3)(n+1)(n+2)=(n2+3n)(n2+3n+2)= [(n2+3n+1)-1][(n2+3n+1)+1]=(n2+3n+1)2-1, 所以, n(n+1)(n+2)(n+3)+1=(n2+3n+1)2. 定理2设K、D是非负整数且K 的非负整数组(x,y)是不定方程Kx(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3)(x>0,y>0)的解. 证明由引理知,x(x+1)(x+2)(x+3)+1和y(y+1)(y+2)(y+3)+1都是平方数,所以设 u2=x(x+1)(x+2)(x+3)+1,v2=y(y+1)(y+2)(y+3)+1, 则不定方程Kx(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3)可转化为不定方程Ku2+(D-K)=Dv2. 设u=v+h(u,v,h∈Z),有: Ku2+(D-K)=K(v+h)2+(D-k)=Dv2, 得: (D-K)v2-2Khv-[Kh2+(D-K)]=0. 则 设w2=DKh2+(D-K)2,当不定方程w2=DKh2+(D-K)2有解(w,h)时,可得: 因u2=x(x+1)(x+2)(x+3)+1和v2=y(y+1)(y+2)(y+3)+1,所以可得: 即 从而得: 例3求不定方程6x(x+1)(x+2)(x+3)=7y(y+1)(y+2)(y+3)(x>0,y>0) 的解. 定理3设K、D是互素非负整数且K 的非负整数组(x,y)是不定方程Kx(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3)(x>0,y>0)的解. 证明由引理知,x(x+1)(x+2)(x+3)+1和y(y+1)(y+2)(y+3)+1是平方数.设u2=x(x+1)(x+2)(x+3)+1和v2=y(y+1)(y+2)(y+3)+1,则不定方程Kx(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3)可转化为不定方程Ku2+(D-K)=Dv2.当不定方程Ku2+(D-K)=Dv2有整数解(u,v)时,由 得: 从而得: 例4求不定方程x(x+1)(x+2)(x+3)=34y(y+1)(y+2)(y+3)(x>0,y>0) 的解. 解设D=34,w2=34h2+332.由例2知,不定方程w2-34h2=332的整数解(w,h)为: 再根据定理2,将(w,h)代入公式: 例5求不定方程x(x+1)(x+2)(x+3)=3y(y+1)(y+2)(y+3)(x>0,y>0) 的解. 将(u,v)代入公式: 推论1设D是非负整数,对不定方程x(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3),如不定方程w2-Dh2=(D-1)2有整数解(w,h),则满足 的非负整数组(x,y)是不定方程x(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3)(x>0,y>0)的解. 证明设K=1.由定理2得,如不定方程w2-Dh2=(D-1)2有整数解(w,h),则满足 的非负整数组(x,y)是不定方程x(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3)(x>0,y>0)的解. 4不定方程Kx(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3)(x>0,y>0)的求解结果 设x、y是非负整数. (1) (7,4)是不定方程x(x+1)(x+2)(x+3)=6y(y+1)(y+2)(y+3)的解; (2) (8,3)是不定方程x(x+1)(x+2)(x+3)=22y(y+1)(y+2)(y+3)的解; (3) (7,2)是不定方程x(x+1)(x+2)(x+3)=42y(y+1)(y+2)(y+3)的解; (4) (5,1)是不定方程x(x+1)(x+2)(x+3)=70y(y+1)(y+2)(y+3)的解; (5) (6,1)是不定方程x(x+1)(x+2)(x+3)=126y(y+1)(y+2)(y+3)的解; (6) (7,4)是不定方程x(x+1)(x+2)(x+3)=6y(y+1)(y+2)(y+3)的解; (7) (5,3)是不定方程3x(x+1)(x+2)(x+3)=14y(y+1)(y+2)(y+3)的解; (8) (7,6)是不定方程3x(x+1)(x+2)(x+3)=5y(y+1)(y+2)(y+3)的解; (9) 对非负整数D,当D>4时,(D-3,D-4)是不定方程(D-4)x(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3)的解.1 不定方程x2-Dy2=M2解的参数形式



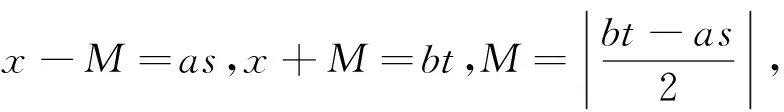
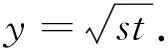
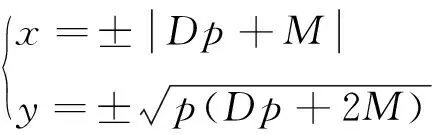


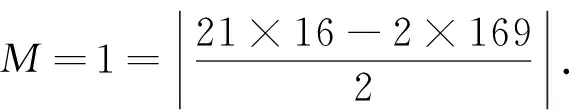
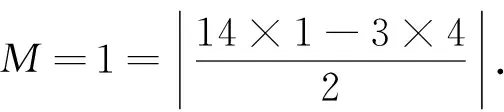

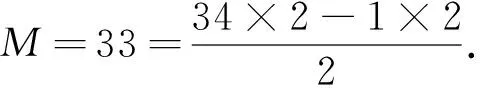
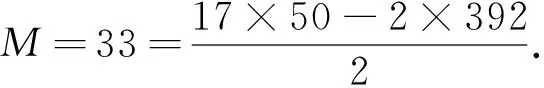

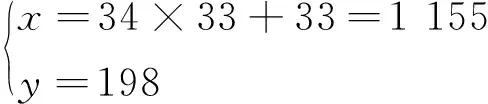

2 不定方程Kx(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3)(x>0,y>0)的求解公式
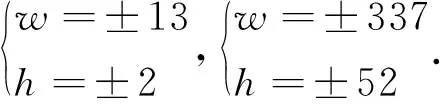

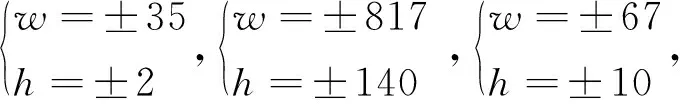


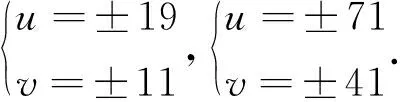

3 不定方程x(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3)的求解公式

