采纳CBDC 的博弈论分析
蔡维德,牟晨琪,姜晓芳,杨冬
(1.北京航空航天大学 计算机学院,北京 100191;2.北京航空航天大学 数学科学学院,北京 100191)
一、引言
数字货币的不断发展,尤其是锚定主要国际货币的稳定币(Stablecoins)的发展,对国际货币体系产生极大冲击,作为应对,各国央行对发行央行数字货币(CBDC)更加积极,美联储(Fed)、欧洲央行(ECB)、中国人民银行(PBoC)、英国央行(BoE)等许多央行都宣布了CBDC 项目,世界银行、国际货币基金组织(IMF)、国际清算银行(BIS)等众多国际组织也已启动CBDC 研究。
英国央行首先提出CBDC 计划,得出的一个研究结论是,现有私营数字货币存在严重问题,这些问题通常与分布式账本的可行性无关,而是与其高昂的交易验证成本有关。发行CBDC 可能会通过放弃纯粹的分权式设计而避免这些成本,同时仍然保留分布式账本的好处[1]。Bordo 和Levin[2]预测,如果一国不开发自己的CBDC 项目,未来将面临金融风险。IMF 建议每个国家都要制定自己的CBDC 计划,与加密货币竞争。IMF 还认为,私营机构发行的稳定币会对金融业产生深远影响。当由大型科技公司或平台(Big Techs)发行,全世界通用时,稳定币就成为全球稳定币(Global Stablecoins,GSC),如脸书(FacebooK)的Libra 就是GSC。2019 年7 月IMF 的报告《数字货币的崛起》[3]称,如果一种GSC 得到央行支持,其行为就像CBDC。这种新数字货币被称为合成CBDC,它不是CBDC,但与CBDC 一样,其储备货币存在央行,因此不存在信用风险。但这会造成合成CBDC 与法定货币之间的竞争,因为人们可能更愿意使用这些GSC,而非本国的法定货币,如果GSC 应用广泛,国内计价单位可能会让位于GSC,造成货币定价权转移,使得央行丧失货币政策控制权。这也将在商业银行和寻求存款的GSC 发行实体间形成另一种竞争。2019年8 月23 日,英国央行前行长马克·卡尼(Mark Carney)表示,一种合成霸权数字货币可能取代美元成为世界储备货币。这又是一种竞争,一种合成CBDC 可能会与美元或任何其他法定货币竞争世界储备货币地位。
目前,对货币竞争已形成共识,由于CBDC或合成CBDC 而产生了各种竞争,包括在GSC 和法定货币之间的竞争,在GSC 和GSC 之间的竞争以及不同CBDC 或合成CBDC 之间的竞争。
开发CBDC 是一项具有挑战性的任务,因为这将影响到方方面面,包括国家货币政策、监管政策、技术解决方案、安全问题以及消费者保护问题。而且,有些国家可能现在还不具备自己开发CBDC 的能力。那么,面对来自他国CBDC或合成CBDC 的竞争,一国是否应该开发自己的CBDC?CBDC 或合成CBDC 会使银行结构改变,占据传统法币的市场份额,但影响将会有多大?关于这些领域的定量分析十分匮乏。
笔者对此进行了突破,从博弈论角度[4]-[7]对CBDC 或合成CBDC 引入的各种竞争进行了理论研究的首次尝试,运用博弈论方法研究了特定国家是否会尝试开发自己的CBDC 项目,并通过定量分析得出CBDC 竞争成功的要素。
笔者的主要贡献如下:运用博弈论模型,从收益和损失两方面分析一国是否应实施CBDC 计划,并根据模型,得出各国最终都会实施CBDC计划,从而印证了2017 年IMF 的建议。同时通过市场份额变化体现竞争结果,调整相关要素,运用计算机模拟方法,发现了采纳CBDC 竞争成功的三要素:初始市场份额、技术能力和先行与否。
一、博弈论背景
博弈论是研究二人或多人在平等的对局中各自根据对方策略变换自己的对抗策略,以达到取胜目的的理论。博弈最初主要研究象棋、桥牌、赌博中的胜负问题,人们对博弈的把握停留在经验层面,没有向理论化方向发展。近代对于博弈论的研究,始于策梅罗、波莱尔及冯·诺依曼。
1928 年,冯·诺依曼证明了博弈论的基本原理,从而宣告了博弈论的正式诞生。1944 年,冯·诺依曼和摩根斯坦共著的划时代巨著《博弈论与经济行为》将二人博弈推广到n 人博弈结构,并将博弈论系统地应用于经济领域,从而奠定了这一学科的基础和理论体系。博弈论现已成为经济学的标准分析工具之一。但对CBDC 或合成CBDC 引入的各种竞争,用博弈论方法进行分析的文献几乎没有,笔者是在此领域的首次尝试。
1950—1951 年,约翰·福布斯·纳什利用不动点定理证明了均衡点的存在,为博弈论的一般化奠定了坚实基础。纳什的开创性论文《n 人博弈的均衡点》(1950 年)、《非合作博弈》(Nash,1951 年)[8]等等,给出了纳什均衡(Nash equilibrium)①的概念和均衡存在定理。此外,莱因哈德·泽尔腾、约翰·海萨尼的研究也对博弈论发展起到推动作用。今天博弈论已发展成一门较完善的学科,是使用严谨的数学模型研究冲突对抗条件下的最优决策的依据。参与者、各参与者的策略集、各参与者的效用函数,是博弈最重要的基本要素。笔者建立的博弈模型中参与者为两个,在复杂博弈模型中通过效用函数计算出CBDC 博弈的纳什均衡。
曾任职英特尔高级行销主管和副总裁的达维多[9]认为,任何企业在本产业中必须不断进行产品更新换代。如果要在市场上占据主导地位,企业就必须第一个开发出新一代产品,又第一个淘汰老产品。达维多法则强调,进入市场的第一代产品能自动获得50%的市场份额,所以任何企业必须首先淘汰自己的产品。达维多法则的理论基点,是着眼于市场开发和利益分割的成效。人们在市场竞争中无时无刻不在抢占先机,因为只有先入市场才能更容易获得较大份额和高额利润。笔者将会对CBDC 经济模式是否遵循达维多定律进行分析。
英国技术工程师兰彻斯特提出兰彻斯特法则[10],探索兵力的比率和损害率之间的关系。兰彻斯特法则分为第一法则(单兵战斗法则)和第二法则(集中战斗法则),再由这两个法则,导出弱者战略(第一法则的应用)和强者战略(第二法则的应用)。后来被运用到市场竞争中,对于努力重建支离破碎的经济和重入世界市场的日本人来说,兰彻斯特的战斗方程式和集中原则的应用成为实现这一目标的一个重要因素。Taoka[11]的案例研究以及Onoda[12]的数学理论导致了基于兰彻斯特方程和重要市场份额价值和比率的公司间竞争模型的发展,将兰彻斯特的两条法则用于战略和战术营销,即兰彻斯特战略。当两竞争对手间市场占有率之比超过射程距离(关键市场份额比率为1.7,这时弱者反败为胜的几率为0)时,弱者应及时放弃经营,另辟蹊径。该模式还提供了市场占有率的目标管理指标,垄断的最佳市场份额为73.9%,此时将独占市场,而不论对手的个数和实力如何;26.1%是市场占有率的下限目标,如果没有一家公司的市场占有率超过26.1%,那么市场就不稳定,公司的相对地位也会迅速变化;控制市场的市场份额为41.7%,当市场占有率达到41.7%时,公司进入相对安全圈,这是参与竞争的首要目标。笔者通过实验证实了CBDC竞争也符合兰彻斯特战略,即如果一个实体获得41.7%的市场份额,它就可能成为新的市场领导者。所以,即使技术落后,一国也应先发制人,不管市场份额如何;而一国有了先进技术,无论是为了保持市场份额还是获得更多市场份额,都应先发制人。
二、当前数字货币竞争研究综述
当前,国际组织、央行和学术界关于数字货币竞争的研究如雨后春笋般不断涌现,按照研究内容,大体可分为四类。
(一)数字货币竞争会使金融市场发生改变,并可能造成外汇和储备金份额的变化。
2019 年7 月,IMF 发布报告《数字货币的崛起》,其中一个主要观点是人们会出于方便而选择各种货币形式。报告除了提出合成CBDC 的概念,还指出数字货币竞争会造成金融市场重组,经历共存、互补和替代三个阶段。
2020 年10 月,IMF 发布《跨境数字货币——宏观金融影响》报告[13],说明数字货币竞争会产生巨大影响,可能造成外汇和储备金份额的变化。注意这里的变化不是增长的变化(2016 年英国央行研究报告认为使用CBDC 会使国家GDP 增长3%,这是增长的变化),而是一种货币的市场份额被另一种货币取代(市场整体份额可能并未变化),所以是新型货币“战争”。
2020 年1 月,欧洲央行发布研究报告《分级CB-DC 和金融体系》[14]。其中描述了数字货币对金融账户的影响,可以概括为两国的情况,其中不对称的情况尤其令人感兴趣。如A 国发行的CBDC 也可能在B 国广泛使用,B 国央行发现其外汇储备减少了,其减少量为B 国家庭所持有的A 国发行的CBDC 量。在固定汇率制下,B 国央行外汇储备因B 国持有新数字货币而下降。
2020 年5 月,欧洲央行发布了一份报告[15],报告在三种不同情况下研究了Libra:作为一种普遍的支付手段,作为一种受监管的价值存储,作为一种不受监管的价值存储。研究人员估计,在最后一种情况下,全球Libra 储备的规模可能接近3 万亿欧元,并可能成为欧洲最大的货币市场基金(MMF)。而即便Libra 在推出后反响平平,其可能的储备规模也将达到1527 亿欧元。
(二)平台将成为金融市场中心,形成网络效应,支持数字货币成为世界储备货币。
普林斯顿大学教授Brunnermeier 等提出了数字货币区(DCA)理论[16],这是影响国际货币金融体系未来形态最具颠覆性的概念。数字货币是因为网络连接所产生的新型货币,但因为国家间的竞争造成数字货币在世界范围内分区,所以称为DCA。DCA 理论指出金融市场将发生重大变革,平台代替银行成为金融市场中心,并形成网络效应,平台管理者将具有显著经济优势。此外,网络效应助力支付,支持数字货币成为世界储备货币。数字货币主要用于交易,因为方便快捷,7×24 小时全天候运行,对客户吸引力大,客户黏性强。商家一旦使用数字货币,往往会留存部分资金在该数字货币上,方便下次交易使用。而一个大国可利用大型DCA 鼓励世界贸易使用本国发行的数字货币。
2019 年6 月18 日,天秤座协会(Libra Associa-tion)发布了白皮书第一版,2020 年4 月16 日,又发布了Libra 2.0 白皮书(Libra 现在已改名为Di-em)。IMF 曾表示,GSC 可通过将托管机构(如商业银行)储备转为央行储备,成为合成CBDC,它在许多场合实际和CBDC 一样。这样央行不需要自己具备开发CBDC 的技术,Diem就采取这一策略,愿意向全世界各国央行提供CBDC 技术。如果一国或地区担心自己的法定货币会被Diem 取代,Fa-cebook 将与其央行合作,为该国开发CBDC,并让其在Diem 平台上运行。由于这种CBDC 发行量还是由央行控制,国家货币政策控制权仍掌握在央行手中。这样Facebook实际上就从数字货币发行转成构建数字货币云平台,即Diem 平台,世界各国的CBDC、GSC 甚至其他稳定币都能在其上运行或交易。很明显,这是Facebook 在私有网络平台里提供了自己的支付工具和货币(虽然锚定于法币),并以数字形式进行支付和交易,这就是DCA 的现实版,所以引发世界金融界极大震动。
(三)数字外币取代是逐步完成的,应对被数字外币取代,CBDC 可能是最佳防御方法。
2020 年10 月,IMF 发布《跨境数字货币——宏观金融影响》报告[13],其中提到CBDC 和GSC采用造成的货币替代问题。IMF 认为CBDC 和GSC 会对法币产生货币替代,将给一国的货币政策带来巨大压力,同时给监管造成困难,即使是官方以禁令的形式进行遏制,如果没有有效的科技手段,仍然很难形成实际的管控力。一旦形成习惯,外币对国内法币的替代往往是高度持久的。
IMF 在2019 年报告中说数字货币占据传统法币的市场份额,数字货币以后可能“完全取代”传统货币,改变比例非常之大。IMF 同时指出这种取代是逐步完成的,不是一次到位。报告中分共存、互补和替代三大步骤,传统法币市场份额将从100%降到0%。
DCA 理论指出应对被数字外币替代的影响,CBDC 可能是最佳防御方法。一个经济体的法定货币被其他数字货币所取代,即数字货币将与法定货币竞争。经济或外交上对大型DCA 开放的经济体尤其容易受此影响,即便拥有稳定货币。最佳防御方法可能是以数字形式发行自己的货币,即发行CBDC。除了货币政策和金融稳定,发行CBDC 可能有更为根本的理由:使本国货币适应新的技术状况,并在此过程中保护它们免受基于数字优势的外部竞争。
(四)数字货币竞争看似种类繁多,但其实最主要的就是国家之间的数字法币竞争。
综观各类文献,可以看到存在各种货币竞争关系,包括地下货币与合规货币之间的竞争、数字法币与合规货币之间的竞争、数字法币和传统法币的竞争,以及国和国之间的货币竞争,其中地下货币和合规货币的竞争影响较小。
而Meta 的Diem 系统,在2020 年4 月宣布弃币保链,即放弃霸权数字货币而保跨境的区块链系统。Diem 币(私营数字货币)主动让位给国家主权的数字货币,如果一个国家要发行主权CB-DC,Diem 币就自动退出,转而支持该国的CBDC。Diem 币是当前最大的数字货币系统,如果Diem 币在国家主权货币前都必须退让,其他私营数字货币更不可能和基于国家主权的数字货币竞争。这样,世界货币竞争其实就是国与国之间的数字法币竞争。
笔者研究国家主权货币竞争模型,通过市场份额变化体现竞争结果,基于我们在英文会议论文中提出的博弈模型[17],开展了系统的实验设计,并进行结果分析,得出四个重要结论。
三、博弈模型和假设提出
(一)简单博弈模型
对于一个特定国家来说,它有两种选择:采用CBDC 还是不采用CBDC。为简单起见,我们假设只有两个国家C1和C2在金融市场上竞争。
假设E1是国家C1因为国内CBDC 项目的成功所获得的收益,H1是C1的CBDC 项目成功对国家C2造成的损失。E2和H2的含义也类似。
一个成功的国内CBDC 项目所获得的好处包括改善其国际金融地位、获得储备货币地位、为那些不能发展自己的CBDC 的国家提供相同的服务和共享平台以及管理数字货币平台。根据DCA理论,拥有平台的实体或国家将比其他没有平台的实体或国家具有显著优势。
成功的国外CBDC 项目所造成的损失包括国际货币状况恶化、可能发生重大金融危机、丧失国家货币政策管理能力。
在数字经济中,根据达维多定律,先行者将比跟随者具有显著优势。这项定律说明,第一个进入市场的产品自动获得50%的市场份额。如果CBDC 的经济模型遵循达维多定律,这意味着那些最先行动的实体将主导市场,这适用于央行或私营机构发行的CBDC。在这种情况下,如果国家(或实体)C1开发了CBDC 项目,而国家(或实体)C2不开发CBDC 项目,则C1将获得超过50%的市场份额的显著优势。根据DCA 理论,C1将具有显著的经济效益。
假设国家C1采用CBDC 项目的成功率为αi,i=1,2。如如果C1技术先进,那么α1 将接近1。这两个国家之间的博弈模型如下表1 所示。
如果国家C2决定开发CBDC 项目:如果C1决定开发CBDC,则得到E1α1−H2α2;如果C1决定不开发,则得到−H2α2。显然E1α1−H2α2比−H2α2大,因此C1应该开发自己的CBDC。
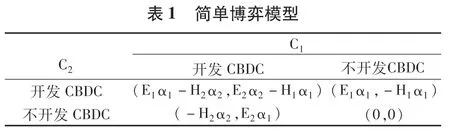
如果C2决定不开发它的CBDC 程序,那么C1还是应该选择开发CBDC,因为开发的好处是E1α1,而不开发CBDC 的好处是0,E1α1显然更大。因此,无论C2如何选择,C1都应该开发自己的CBDC 项目。
同样,无论C1选择什么,最终C2需要发展自己的CBDC 项目。在这种情况下,这两个CBDC 项目都将发展成一个纳什均衡模型。
但是,C1和C2的收益E1和E2不同,损失H1和H2也不相同。如果C1在经济上很强大,但不发展其CBDC 项目,那么可能造成的损失将是巨大的,因为它可能会失去其重要经济地位。然而,如果C1发展CBDC,而国家C2不发展,C2将会进一步落后。
成功的概率αi是时间的函数,并随时间的推移而增加,因为会有更多的研究成果可用,并且每个国家最终都将能够开发出自己的CBDC项目。一个发达国家因为技术优势更强,可能比其他国家先达到1,并取得达维多优势。但最终两者都将接近1,这意味着每个国家都将制定自己的CBDC 计划。只是先行者将拥有更多市场份额。
(二)复杂博弈模型
现在,我们试图建立一个更为复杂的博弈论模型来分析一国或实体在选择CBDC 时的盈亏情况。其盈亏仅仅体现在市场份额变化上,因为与市场份额变化相比,为CBDC 进行经济转型的成本微不足道。
如上所述,让我们关注最简单的两人博弈,博弈者为C1和C2,当前市场份额分别为M1和M2,其中M1+M2=1。设S1=S2={Y,N}是C1和C2的纯策略集,其中Y 和N 分别代表采用和不采用CBDC。当i=1 和2 时,效用函数pi是从S1×S2到[-1,1]的映射p(is)表示给定纯策略s=(s1,s2)时C1的收益(s1∈S1和s2∈S2)。
对于i=1 和2,混合策略σi是Si中纯策略的概率分布,其中σ(is)是Ci选择纯策略s 的概率(s ∈Si)。用∑i 表示由Ci的混合策略组成的空间。我们可以将Ci采取混合策略σ=(σ1,σ2)∈∑1×∑2 时的收益定义为

该收益基本上是概率分布σ 时Ci的预期收益。
对于任何纯策略s1∈S1和s2∈S2,如果混合策略σ*=(σ1*,σ2*)∈∑1×∑2 称为博弈的纳什均衡。纳什均衡是指博弈中的每一个博弈者在其他博弈者的混合策略是固定的条件下期望收益最大化的状态,因此任何试图从纳什均衡中改变其混合策略的人都将面临收益减少的情况。对于有限非合作博弈,至少存在一个纳什均衡。
在这个模型中,我们将计算博弈的纳什均衡,以揭示某个参与者采用CBDC 的概率。为此,我们需要效用函数的显式表达式。
(三)效用函数
我们考虑一个时间t 的动态博弈。博弈的参与者C1和C2,他们的纯策略{Y,N}无论何时都保持不变。但他们的效用函数p1和p2确实会随着时间t 变化,我们将会在下面进行解释。为了简化我们的模型,时间被离散化为只取非负整数。在现实世界中,假设时间段[t0,t0+1]为3 个月。
对于博弈中的每个参与者来说,如果选择采用CBDC,则成功率为P(it)。这个概率有一个初始值P(i0)=Pi,并且随着时间的推移而增加(底层相关知识和技术存储随时间增加,从而采用CBDC 成功率增加)。我们假设C1和C2的增长率是常数c,因此我们知道成功的概率是P(it)=min{ct+Pi,1},i=1,2。当Ci 选择在某个时间采用CBDC,经过一个筹备期d,Ci在时间+d 会成功的概率是
接下来,我们将讨论四种可能的纯策略组合下每一个参与者的回报。从根本上说,在这个博弈中,如果C1 选择采用CBDC 而成功,而C2 失败或选择不采用CBDC,则C1 获得C2 的部分市场份额,反之亦然。假设在某个时间,C1 完成了它的筹备期,成功采用了CBDC,那么C1 将在获得C2 的部分市场份额。用M1(t)和M2(t)表示与之相关的市场份额,设(r0 组合二,在时间是(Y,Y):在这种情况下,C1和C2都选择采用CBDC,他们的收益取决于谁先成功。由于成功率的函数是P(it)=min{ct+Pi,1},并将线性增长到1,我们知道存在一个且仅一个成功采用CBDC 的参与者的最大可能时间长度是其中: 组合四,在时间是(N,Y):上述第三种情况的又一种情形。 在C1和C2的效用函数已知的情况下,我们最终可以计算博弈的纳什均衡。假设σ*=(σ1*,σ2*)∈∑1×∑2 是博弈的纳什均衡,那么C1选择采用CBDC 的概率是σ1*(Y),C2是σ2*(Y)。 我们在复杂博弈模型的对比实验中对市场份额损失率做了三种假设,市场份额损失率最大设定为10%,相比较IMF 报告中100%的下降更为合理。 笔者论证基于三点假设:一是CBDC 带来的收益是真实的;二是CBDC 带来的损失是真实的;三是随着时间的推移,开发CBDC 的成功率不断提高。Meta 的Libra 在2019 年对央行和商业银行的影响证明了前两个假设是现实的。此外,区块链或相关技术在过去12 个月里有了显著的改进,出现了新理论、新架构、新框架、新监管技术。Li-bra 2.0 也改进了其监管机制,将嵌入式监管纳入其中。因此,第三个假设也是现实的。 在本节中,我们首先确定上一节中列出的参数值,间隔[t,t+1]表示现实世界中的3 个月。准备时间d=6。 基本实验中参数设置如下: ——市场份额M1=0.9,M2=0.1,参与者C1占据绝大部分市场份额。 ——初始成功率P(10)=0.5,P(20)=0.3,成功率的增加率r 设为0.05。 ——市场份额损失率r=0.1(3 个月内):这意味着,对一个参与者而言,如果其他参与者成功而他没有成功,则在3 个月内失去10%的市场份额。 ——市场份额损失m=0.3。 基于上述参数设置,计算出第4.3 节中组合二的收益。在这种情况下,C1 和C2 都选择在t=0 时采用CBDC。当t=6(18 个月的准备期后),C1 成功率为0.5,C2 成功率为0.3。让我们进一步计算Ci 第一次成功的概率P~(it),如下表所示。 从上表中,我们可以看出,C1在t=6 时第一次成功的概率且C2在t=7 时第一次成功的概率是0.5×0.7×0.35=0.5×0.245=0.1225。在这样的组合中,C1的总收益是(7-6)×3=3 个月吃掉的C2市场份额为r×M2=0.01。同样,C2收益为−0.01。遍历上表中的所有可能的组合,我们将能够计算纯策略配置(Y,Y)下C1和C2的预期收益。 我们实现算法来计算4 个纯策略组合的显式收益。对于上面列出的参数值,计算收益如下表3 所示。 有趣的是,表3 显示,如果目前市场份额占主导地位(90%)的国家C1不采用CBDC,而另一个拥有10%市场份额的国家C2采用CBDC,则C1将损失大约19.2%的市场份额,这一损失对C1而言太大了。 这一结果部分证实了CBDC 经济模式遵循达维多定律,即第一个采用CBCD 项目的国家将从未采用CBCD 项目的国家手中获取大量市场份额。 接下来我们将表3 中的效用函数输入到Gam-bi[t18]软件中计算纳什均衡,C1的纳什均衡为(1,0),C2的为(1,0),这意味着C1和C2都将选择应用CBDC 的概率为1。这与前面得出的分析结果一致。 下一步,我们分别调整市场份额初始值、成功率初始值、市场份额损失率以及先行与否,看这些要素对博弈结果的影响。每张图中,Case 2是C1和C2同时开发CBDC;Case 3 是C1选择开发CB-DC;Case 4 是C2选择开发CBDC。 1.市场份额初始值M1,M2对市场份额变化的影响 调整M1,M2,也即模拟两者在不同的市场份额下进行实验,看市场份额的变化情况。 (1)初始成功率P(10)=0.5,P(20)=0.3,市场份额损失率r=0.1(3 个月内): 可以看出市场份额增长与初始市场份额成反比,初始市场份额越小,能够获得的市场份额增长越大,这也是我们通常所说的追赶者效应。 而无论是C1还是C2,当其市场份额为40%时,如果先发制人,则将获得超过10%的市场份额增长,也即其市场份额将超过50%,成为市场主导者。 2.技术优势对市场份额变化的影响 接下来,我们分别调整P1,P2,也即模拟在不同的技术优势下进行实验,看市场份额M1和M2的变化情况。 (1)初始成功率P(10)=0.5,P(20)=0.05,市场份额损失率r=0.05(3 个月内) 图3 P1(0)=0.5,P2(0)=0.05 时M1 的市场份额变化图 (2)初始成功率P(10)=0.3,P(20)=0.1,市场份额损失率r=0.05(3 个月内) 图4 P1(0)=0.3,P2(0)=0.1 时M1 的市场份额变化图 当C1先行时,仅仅初始成功率不同,第一种情况下C1的初始成功率是C2的10 倍,第二种情况下C1的初始成功率只有C2的3 倍。当C1初始市场份额为10%时,第一种情况下C1的市场份额M1增长为25.5%,第二种情况下M1增长为19%,第一种情况比第二种情况市场份额增长高出6.5%;当C1初始市场份额为40%时,第一种情况下M1增长为17%,第二种情况下M1增长为13%,第一种情况比第二种情况市场份额增长高出4%;当C1 初始市场份额为80%时,第一种情况下M1增长为6.5%,第二种情况下M1增长为4%,第一种情况比第二种情况市场份额增长高出2.5%。 当C1后行时,如果技术优势足够大,在初始市场份额较小时,仍然能够获得市场主导地位,如在第一种情况下,初始市场份额为50%到60%之间时,就可以获得正的市场份额增长率,从而占据市场主导地位。但如果技术优势不够大,获得市场主导地位就比较困难,如在第二种情况下,只有在市场份额小于25%的情况下,才能获得正的市场份额增长率,但市场份额增长率有限,不可能获得市场主导地位。 根据以上实验数据结果,可以看出四点:一是技术优势与市场份额增长呈正相关;二是两国技术优势差距越大,先行者的优势越明显;三是当一国初始市场份额越小时,技术优势对先行者的帮助越大;一国刚开始市场份额越小,越需要先行一步,通过先进的技术弯道超车,获得更大的市场份额;四是如果科技非常领先,技术优势明显,即使决策失误,开发CBDC 晚了一些,最后也能追上。 (3)初始成功率P(10)=0.3,P(20)=0.03,市场份额损失率r=0.05(3 个月内) 下面我们再调整一下,C1 的初始成功率仍然是C2的10 倍,但C1和C2的初始成功率都稍微小一些。 当C1初始市场份额为10%时,C1的市场份额M1增长为24%,比前面第一种情况的25.5%少1.5%;当C1初始市场份额为40%时,C1的市场份额M1增长为15.5%,比前面第一种情况的17%s 少1.5%;当C1初始市场份额为80%时,C1 的市场份额M1 增长为5%,比前面第一种情况的6.5%少1.5%。从以上实验数据结果可以看出,初始成功率与市场份额增长呈正相关,在这种情况下,初始市场份额对此影响不大。 图5 P1(0)=0.3,P2(0)=0.03 时M1 的市场份额变化图 3.市场份额损失率对市场份额变化的影响 最后,我们调整r,也即模拟不同的市场份额损失率,按影响从大到小,尽量做到全面覆盖。分成三种情形:一是比较大的影响,市场份额损失率为10%;二是中等影响,为5%;三是较小影响,为1%。从而理解大、中、小市场份额损失率影响市场份额M1 和M2 的变化情况。 (1)初始成功率P1(0)=0.5,P2(0)=0.05,市场份额损失率r=0.1(3 个月内) 图6 市场份额损失率r=0.1 时M1 的市场份额变化图 (2)初始成功率P1(0)=0.5,P2(0)=0.05,市场份额损失率r=0.05(3 个月内): 图7 市场份额损失率r=0.05 时M1 的市场份额变化图 (3)初始成功率P1(0)=0.5,P2(0)=0.05,市场份额损失率r=0.01(3 个月内): 从实验结果数据可以看出,无论市场份额损失率r 大小如何,对市场份额占有都会有影响,但可以明显看出,市场份额损失率r 越大,一国对另一国CBDC 市场份额的取代程度越快。尤其是初始市场份额比较小,又作为先行者时,比如当C1 先行且其初始市场份额为20%时,市场份额损失率r 为10%时市场份额M1增长将近40%,r 为5%时M1增长为22.5%,r 为1%时M1增长仅为5%。 图8 市场份额损失率r=0.01 时M1 的市场份额变化图 CBDC 和合成CBDC 受到各大央行高度关注,也被Facebook 等大型科技公司接受。这不仅带来技术突破,还将重组金融市场,改变国家货币政策。笔者运用博弈论的方法,考虑开发CBDC 的收益及不开发CBDC 或开发不积极可能造成的损失,分析了一国是否会开发CBDC,并采用计算机模拟实验,得出CBDC 竞争成功的三要素。主要结论如下: 一是无论一国目前技术状况如何,由于与他国间的竞争,最终该国将致力于发展CBDC。BIS最近对21 个发达国家和45 个新兴市场经济体的央行进行的调查[19]表明,大约80%的国家正在从事与CBDC 有关的工作,40%的国家已经从分析研究发展到实验或概念证明。这进一步证明我们的结论是正确的。 二是技术是关键驱动力,两国技术优势差距越大,先行者优势越明显。而初始市场份额越小,技术优势对先行者获取市场份额的帮助越大,越有可能弯道超车。如果科技领先,即使决策失误,开发CBDC 晚了一些,最后也能追上,所以科技领先非常关键。这与哈佛大学的罗格夫[20]的观点不谋而合。2019 年11 月,罗格夫认为,新货币战争出现,这是数字版本的货币战争,既涉及受监管的金融市场,也涉及地下市场。他还提到,技术是这些变化的关键驱动力。 三是先发制人会比跟随者获得优势,随着CB-DC 的部署,市场领导地位可能会发生变化。博弈论模型表明,如果目前的市场领导者不采用CB-DC,将有可能失去全球经济市场份额的19.2%。这证实了2017 年Bordo 和Levin 的推测,即CBDC 对国家经济体系和全球市场领导地位影响重大。如一国不是目前的市场领导者,它就有动力抢先部署CBDC,因为研究结果表明,该国可以从目前的领先者那里获得19.2%的收益,而如果一国拥有超过40%的市场份额,并且先发制人,它就可能成为市场的主导者。这证实了兰彻斯特战略,即如果一个实体获得41.7%的市场份额,它就可能成为新的市场领导者。所以,即使技术落后,一国也应先发制人,不管市场份额如何,而一国有了先进技术,无论是为了保持市场份额还是获得更多市场份额,都应先发制人。 四是对于市场份额增长而言,初始市场份额与其呈负相关。技术优势与其呈正相关,先行与否与其呈正相关,当一国的市场份额大、技术薄弱、行动迟缓时,最坏的情况会发生,它可能会失去30%的市场份额。2020 年10 月,IMF 的报告针对154(149)个报告外币存款(贷款)与总存款(贷款)的数据的国家样本计算得出结论,虽然世界上大多数国家的货币替代水平较低,但近三分之一的国家货币替代率超过存贷款的30%。货币替代率高的国家都是新兴经济体或发展中经济体。 根据BIS 于2019 年12 月发布的全球外汇市场调查最终版数据,其中主要货币交易量占比为:美元继续保持第一大货币地位,占比88.3%(5824,036/6595,4711①),与2016 年的占比87.6%相比变化不大。欧元排名第二,占比微升至32.3%。日元交易量仍为全球第三,但从2016 年的21.6%降至16.8%。人民币交易份额占比1.4%,在所有货币中排名第八,是最大的新兴市场经济体货币,这与中国央行较早开展数字货币研究有着千丝万缕的联系。 而2020 年6 月30 日,IMF 公布官方外汇储备货币构成数据显示,2020 年一季度,美元外汇储备总额为6.794 万亿美元,约占已配置外汇储备的61.9%,欧元在外汇储备中的占比稳定在20%,日元在外汇储备中的占比同样稳定在5.6%,人民币的占比为2.02%。美元相比2000 年的外汇储备占比70%,已经有所下降,其中与美元数字货币发行计划落后的联系有待证明。 可以看出,美元现在无论是在货币交易量还是在外汇储备总额中占比仍然很高,是名副其实的市场领导者,因此它更应先发制人,发行CBDC,否则其损失会非常大,而事实上,美国最近的政策也确实如此。而人民币作为一种新兴货币,更应借助这个机会,通过发展人工智能和区块链等先进技术,支持CBDC 发行,从而占据一定的市场份额。


(四)相关假设
五、实验设计与结果分析
(一)基本实验显示先采用CBCD 者将从未采用者手中获取大量市场份额,博弈的纳什均衡状态是双方都会选择采用CBDC
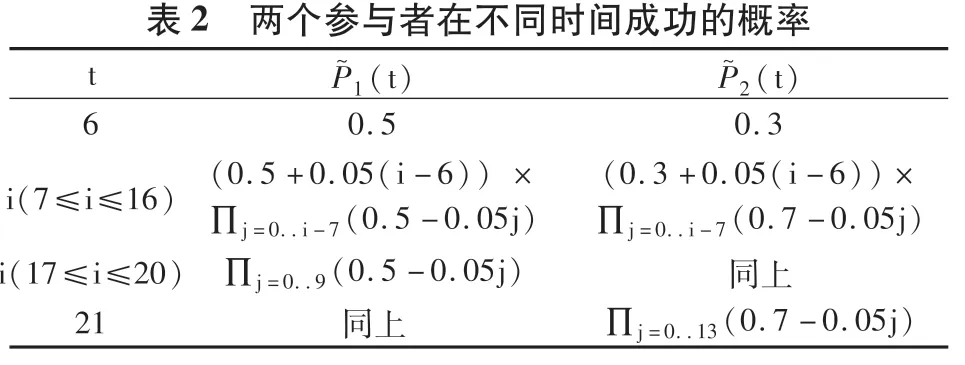

(二)对比实验对比分析市场份额初始值、技术优势和先行与否等要素对博弈结果的影响
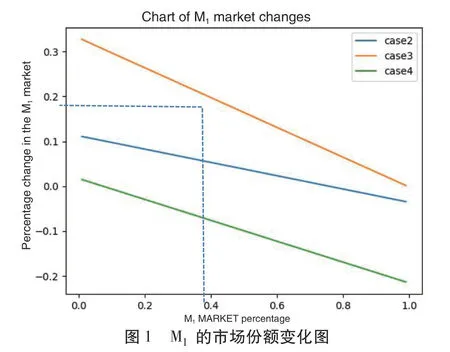
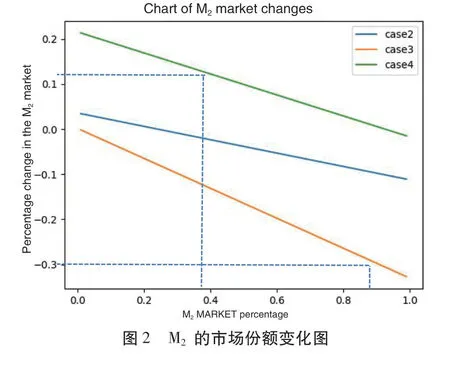
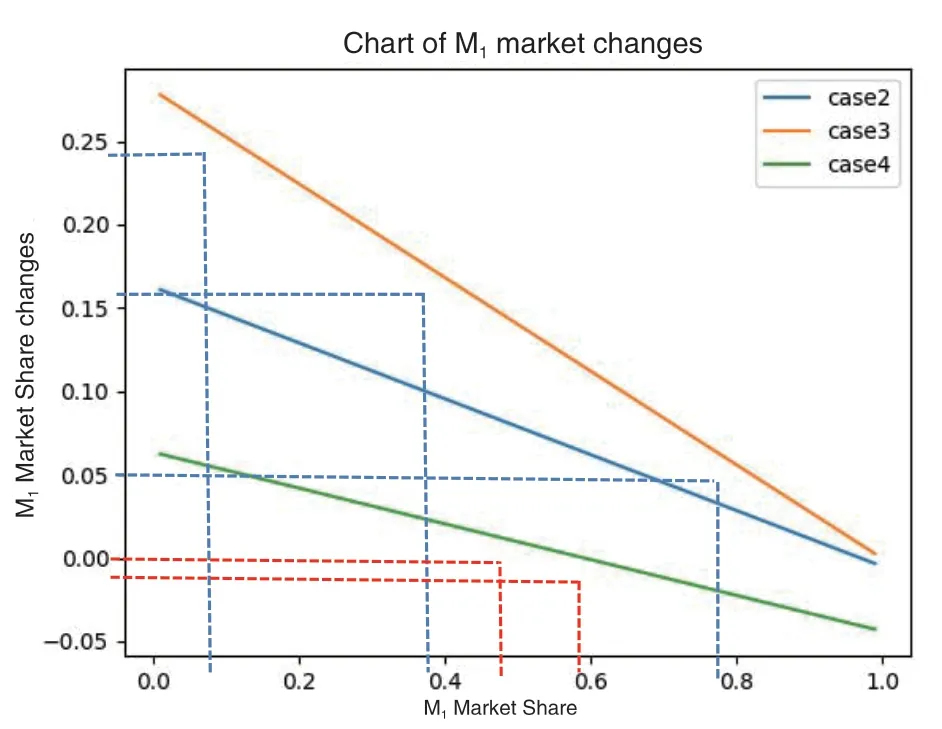
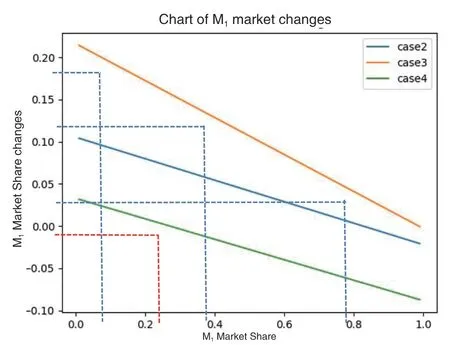
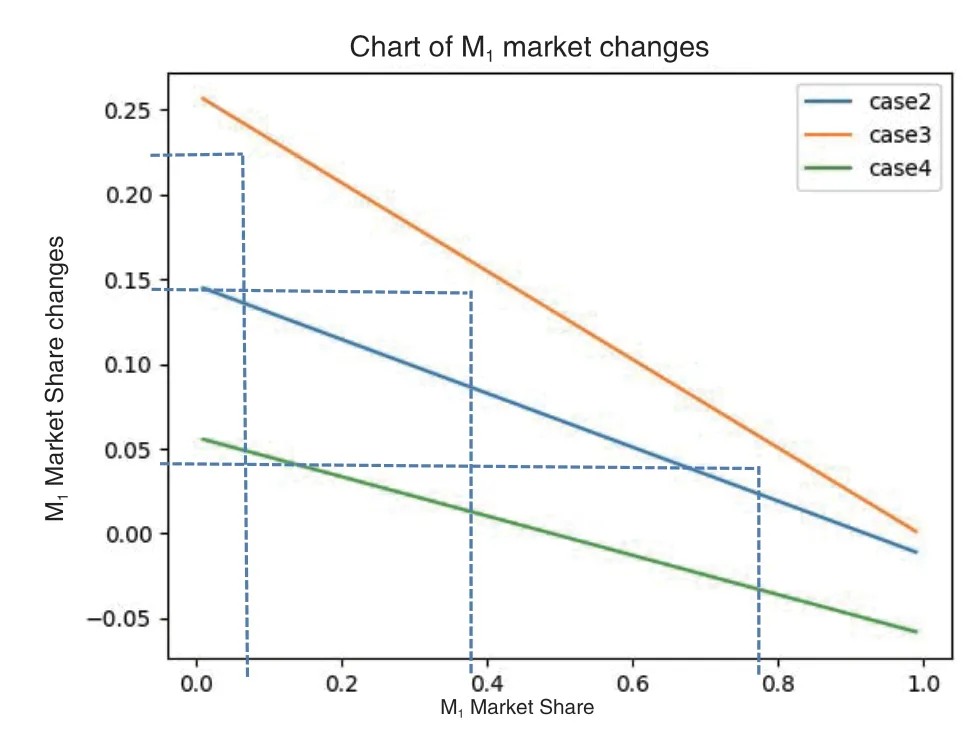
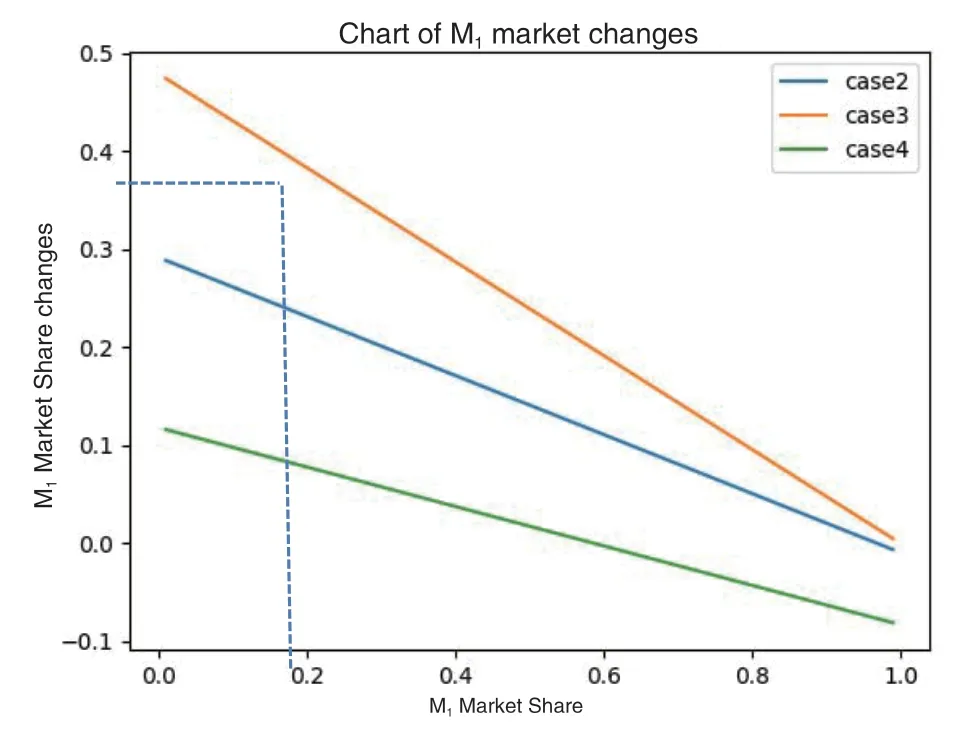
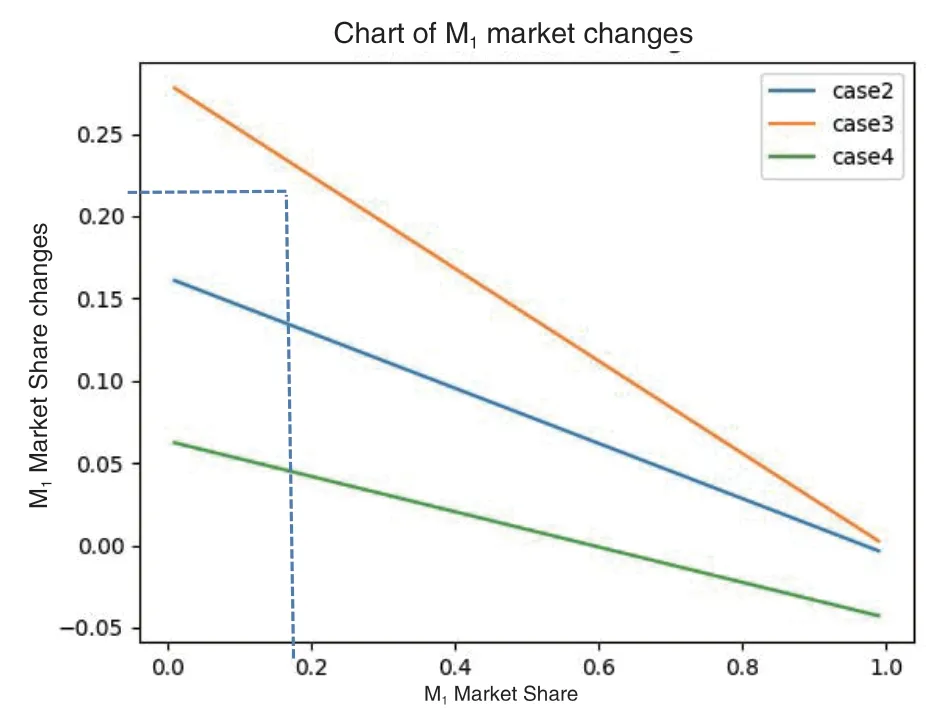
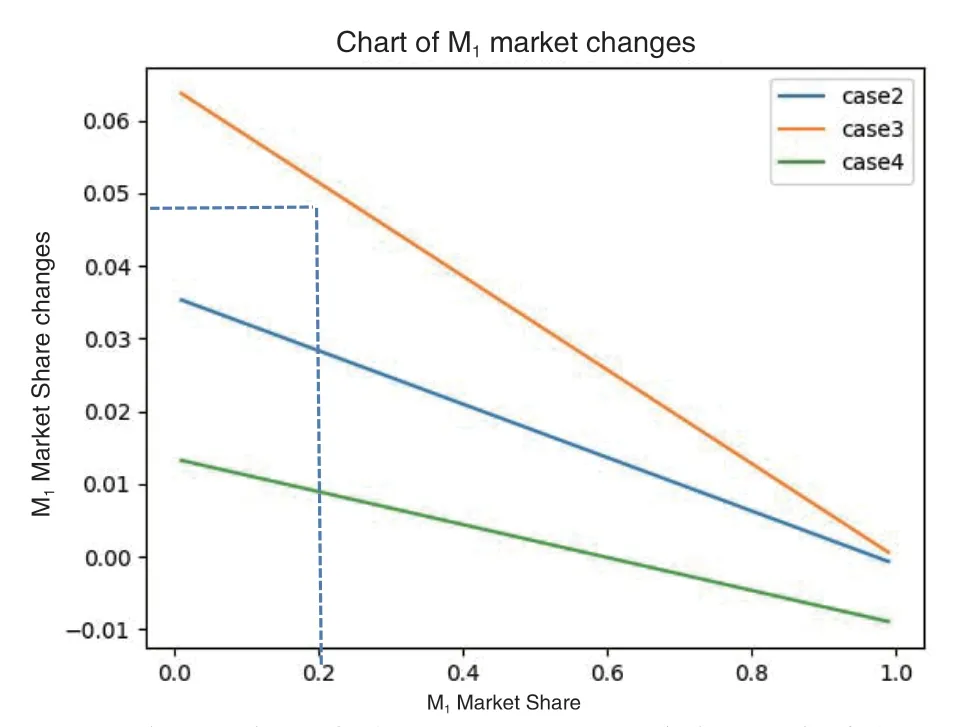
六、结论和建议

