煤层夹矸对巷道围岩稳定性影响研究
张康宁,李 明
(中国矿业大学(北京) 能源与矿业工程学院,北京 100083)
近年来,陕蒙新等西北区域已经成为我国煤炭生产的战略中心,由于煤炭资源赋存条件较好,煤矿的智能化建设与转型在此区域进展迅速。然而,在厚煤层的双巷掘进中,煤巷常出现煤层夹矸结构,直接影响巷道稳定性与掘进效率,从而影响煤矿智能工作面的建设。煤层夹矸特别是软弱夹矸破坏了巷道围岩的连续性与整体性,常成为整个巷道围岩支护结构体的薄弱部分,导致巷道围岩稳定性降低,出现巷道非均匀变形明显等问题。若不采取有效支护措施,则易导致巷帮围岩沿夹矸结构面滑动,进而造成巷道围岩的失稳破坏[1]。
目前,国内外专家学者对含夹矸双巷掘进的煤柱稳定性及巷道矿压显现、围岩破坏规律进行了大量研究[2-6],王自龙[7]、冯腾飞[8]、裴孟松[9]等对不同硬度、厚度、层位夹矸对巷道影响规律进行了深入研究;邵水才等[10]研究揭示了含泥岩夹矸巷道外错变形机理,提出了采用长锚杆加强副帮夹矸层上部煤体的支护对策;王建超[11]、王志强[12]、黄庆享[13]、杨继强[14]等对双巷掘进巷道矿压显现、围岩稳定性及支护进行了研究。此外,不少学者采用理论分析和数值计算方法,分析了巷道围岩矿压显现规律,提出了双巷掘进区段煤柱合理宽度确定原则和方法,并对不同夹矸条件下沿空煤巷复合顶板应力分布和位移变化进行研究,进一步提出了合理的支护方案[15-20]。然而,对于含夹矸巷道的研究,针对单因素对巷道稳定性影响研究较多,而针对多因素共同作用下的影响研究较少。笔者设计了一种基于决策树与正交试验的研究方法,通过采用决策树模型对收集与采集的数据进行分析和建模,选取与夹矸有关的重要参数建立因素水平表,并进一步地通过对夹矸厚度、夹矸坚固性系数及夹矸层位3种因素设计正交试验,分析夹矸对巷道围岩变形的影响规律,同时探究不同煤矸强度比条件下巷道围岩变形规律。在为研究巷道围岩变形提供新方法的同时还可为类似多夹矸煤层巷道布置和支护提供一定的参考。
1 方法概述
通过对收集得到的10个矿井含夹矸巷道位移及相关因素数据进行预处理后,用决策树模型进行训练,通过输入因素参数组合建立决策树回归模型,获得影响巷道围岩稳定性的重要性排序,然后提取其中影响较大的受夹矸影响因素。以实际工程背景为例,通过建立FLAC3D数值计算模型设计正交试验方案,进一步更准确地研究受夹矸多因素共同作用下对巷道稳定性的影响。流程设计如图1所示。

图1 研究方法与流程
2 基于决策树的影响因素重要度研究
2.1 数据选取
通过收集得到10个典型含有夹矸巷道的煤矿基本参数,包括采深、煤层厚度、倾角、煤体坚固性系数与巷道断面等巷道基本参数,以及夹矸位置、夹矸坚固性系数、夹矸厚度等夹矸影响因素,共计 13项基本参数,如表1所示。以巷道围岩位移作为巷道变形程度的评价指标。

表1 巷道变形相关因素及数据类型
这10个含夹矸巷道中煤层夹矸情况也有所不同,夹矸对巷道围岩稳定性也具有不同程度的影响,能够基本反映煤层夹矸的多样性及不稳定性。将上述影响因素作为属性,巷道围岩位移量作为标签,能够综合反映这些因素对巷道稳定性的影响,避免了单一矿井条件的特殊性或某种因素对特定矿井的决定影响等状况导致结果不具备普遍性。数据来源于相关论文及煤矿现场的实测结果,共计155组数据。
2.2 模型建立
通过数据预处理阶段消除异常值及缺失值的影响后,将数据按照70%和30%的比例进行抽取,基于决策树的训练集和测试集,利用python开发环境中的机器学习模块Scikit_learn中的DecisionTree Regression 模型对训练数据集进行回归拟合,拟合准确率达标后利用树模型接口coef_返回特征的权重进行重要度分析。典型含夹矸巷道基本信息如表2所示。

表2 典型含夹矸巷道基本信息
在回归拟合过程中,为了使决策树回归模型达到最优化的效果,主要对决策树中的超参数max_depth(限制树的最大深度)进行优化,这是决策树模型中用得最广泛的剪枝参数,在高维度样本量计算时非常实用,决策树多生长一层,对样本量的需求会增加1倍,所以限制树深度能够有效地限制过拟合。在实际的拟合过程中通过设置max_depth范围在[1,10]区间中逐步进行模拟,选择模拟效果的最优值。为了观察模型的稳定性,采用十折交叉验证法来划分训练集及测试集,以保证模型的有效性,如图2 所示。

图2 十折交叉验证示意图
同时,为了更好地评估回归模型的性能,选用绝对平均误差MAE(mean absolute error)、均方误差MSE(mean squared error)及准确率(Accuracy)作为模型评价指标,定义如下:
2.3 结果分析
经过决策树模型不同超参数的优化之后,得到当决策树模型的超参数max_depth=5时,模型取得相对优化结果。此时,模型的均方误差为0.581,绝对平均误差为0.935,此时的准确率达到80.1%。考虑到获取的数据容量较小,排除获取的原始数据的误差,决策树回归算法对训练集与测试集已经有了比较好的适应性,此模型能基本说明相关参数对含夹矸巷道的影响程度。
精确度最高时(max_depth=5)决策树模型的特征重要度排序如表3所示,表明模型中对含夹矸巷道围岩稳定性影响较大的因素的排序。从表3中可以看出,巷道的基本参数对巷道围岩稳定性起着决定作用,其中巷道埋深对含夹矸巷道位移量影响最大;其次,位移发生的部位不同,位移量也有所区别;煤层厚度对巷道位移量也有重要的影响。这三项基本参数在影响因素重要度中排名前三位。巷道含夹矸对其稳定性也有着重要的影响,其中,夹矸坚固性系数、夹矸位置及夹矸厚度分别排在含夹矸巷道影响因素排序的4~6位。

表3 含夹矸巷道围岩稳定性主要影响因素特征重要度排序
为了进一步研究夹矸对巷道稳定性的影响方式与程度,以神华布尔台煤矿12上煤三盘区掘进工作面巷道为工程背景,选取通过决策树训练得到的对巷道围岩稳定性影响较大的夹矸坚固性系数、夹矸层位及夹矸厚度3个重要因素设计正交试验,探究夹矸多因素共同作用下对巷道围岩稳定性的影响。
3 工程背景
神华布尔台煤矿12上煤三盘区位于该矿井田西部,埋深317~402 m,煤层倾角1°~3°,为近水平煤层。煤层全层厚度0~7.10 m,平均厚3.01 m,但厚度变化较大;含夹矸0~5层,一般含夹矸0~3层,夹矸厚0.1~1.0 m,岩性为砂质泥岩、粉砂岩。煤层上方直接顶以粉砂岩为主,局部为砂质泥岩、泥岩;基本顶以砂质泥岩为主,局部为细粒砂岩、中粒砂岩。该区域煤层结构复杂,不同层位夹矸厚度变化较大,巷道掘进期间受夹矸影响,巷帮变形严重而顶板较为稳定,如图3所示。

图3 巷帮与顶板变形情况
4 基于夹矸因素重要度的正交试验研究
4.1 正交试验设计
为研究夹矸对巷道变形影响规律,选取夹矸厚度、夹矸强度(由于夹矸坚固性系数是反映夹矸强度的重要指标,故直接选取夹矸强度作为试验指标)和夹矸层位3种因素设计正交试验,研究上述3种因素对含夹矸煤层巷道变形影响的显著性大小,在不使用正交表的情况下进行测试,尝试所有可能的方案总共3×3×3=27种,但是出于时间、成本考虑,不能每种都进行试验,这也不符合现场的实际情况。试验优化是正交试验设计时的常用技术,通过优化,可以将27种方案减少至9种,3种因素各选取3个水平,即采用 L9(33)正交试验表设计正交试验。这代表性的9组中具备了“均匀分散,齐整可比”的特点,在以实际夹矸情况为基本前提的情况下,能够较好地反映夹矸厚度和夹矸强度的3个水平,以及夹矸所在的3个不同层位。正交试验各因素水平如表4 所示。
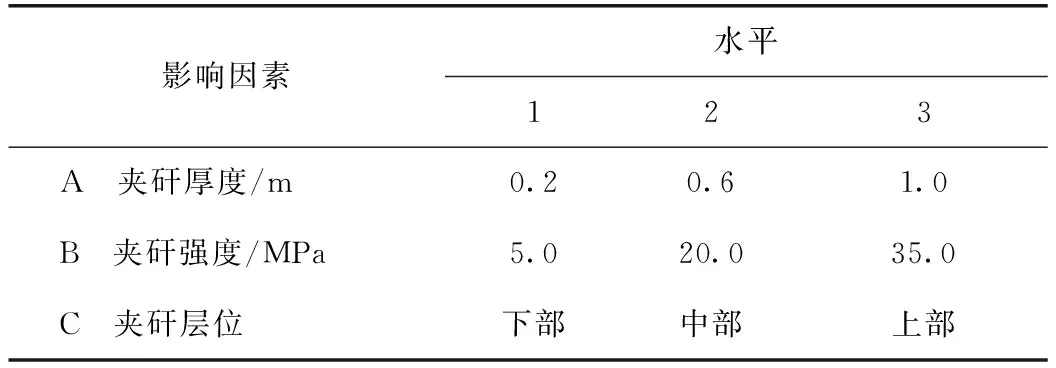
表4 正交试验因素水平
为保证正交试验的准确性,在正交试验表中设置空列,同时考虑反映试验误差等因素的影响,并计算单纯的随机效应,数值计算模型如图4所示。

图4 数值计算模型
采用FLAC3D数值模拟软件进行建模,模型长×宽×高=60 m×50 m×49 m,煤层厚度7.0 m,含夹矸煤巷巷道宽度6.0 m、高度3.8 m,为矩形巷道。模型上边界施加-6.28 MPa面力模拟上覆岩层重量,本构模型采用莫尔-库仑破坏准则,煤岩体力学参数如表5所示。

表5 煤岩体力学参数
对正交试验方案中9组不同参数的模型进行数值计算,除试验选取的3种(A、B、C)因素不同外,9组数值模型的其余参数均相同。正交试验方案及结果如表6所示。

表6 正交试验方案及结果
4.2 巷道围岩变形试验结果分析
将FLAC3D计算结果分别通过极差与方差分析,可得到各因素对巷道变形的影响程度大小与各因素对试验结果影响显著性。
4.2.1 试验结果极差分析
在正交试验完成后对试验结果进行极差分析,如表7所示,其中Ki为各因素i水平对应的试验结果之和,ki为各因素试验结果求平均值,Ri为各因素试验极差。对比各因素极差,当极差不相同时,说明各因素对含夹矸煤巷的影响程度不同,极差越大,说明该因素对巷道变形的影响程度越大;反之越小。

表7 试验结果极差分析
由表7可以看出,影响塑性区发育深度的极差大小规律为夹矸强度(1.27)>夹矸层位(0.33)>夹矸厚度(0.20),说明夹矸强度在上述3个因素中影响最大,夹矸层位次之,夹矸厚度影响最小。影响巷帮移近量因素的极差大小为夹矸厚度(2.07)>夹矸层位(1.09)>夹矸强度(0.76)。
绘制各因素对塑性区深度与巷帮移近量影响的直观图,如图5所示。

(a)夹矸厚度对巷道围岩变形影响
通过分析夹矸厚度、夹矸强度、夹矸层位对塑性区深度与巷帮移近量影响规律,表7中夹矸厚度极差分析平均值k1>k2>k3。由图5(a)可以看出,随着夹矸厚度的增加,塑性区深度逐渐减小,夹矸厚度1.0 m比厚度0.2 m塑性区深度减小0.2 m,减小20.0%,相比其他2种因素,减小趋势并不明显;巷帮移近量减小趋势较为明显,夹矸厚度1.0 m比厚度0.2 m时巷帮移近量减小2.07 mm,减小6.43%。
同理,对比分析夹矸强度对塑性区深度影响,极差分析平均值k1>k3>k2。由图5(b)可以看出,随着夹矸强度的增加,煤体塑性区深度呈现快速减小后趋于稳定的趋势,夹矸强度35 MPa比5 MPa塑性区深度减小1.20 m,塑性区深度减小63.36%。对比夹矸强度对巷帮移近量影响,极差分析平均值k1>k2>k3,夹矸强度35 MPa比5 MPa巷帮移近量减小 0.76 mm,巷帮移近量减小0.79%。
对比分析夹矸层位对塑性区深度与巷帮移近量影响,极差分析平均值k1>k3>k2。由图5(c)可以看出,夹矸在巷道上部、下部时巷道围岩变形较大,夹矸层位在中部时,巷道围岩较为稳定,夹矸位于巷道中部时,塑性区深度比其在巷道上部和下部时分别减小0.14、0.20 m,巷帮移近量分别减小1.09、1.02 mm,巷道稳定性中部>下部>上部。
由以上分析可知,夹矸厚度越大、夹矸强度越高并且夹矸处于巷道中部位置时巷道围岩稳定性最好。
4.2.2 试验结果方差分析
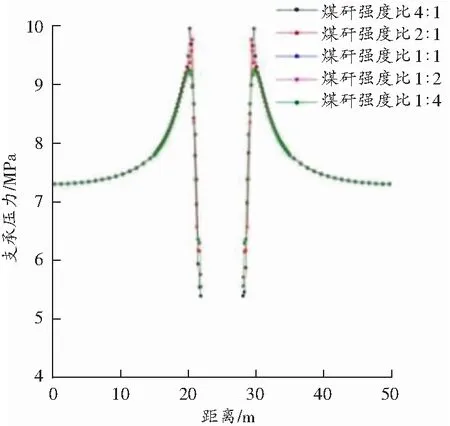
与方差分析相比,极差分析可较为方便地通过相对较少的试验次数得到各因素对试验结果的影响大小,但不能分析多因素试验误差的大小及各因素对试验结果影响显著性。为此,方差分析中通过预留空列为误差列,对正交试验结果进行分析。方差分析基于F检验,认为各试验因素的F>F0.01时该因素对试验结果影响高度显著,F0.05 通过查看F分布分位数表可知,F>F0.01(2,2)=99.0时具有显著影响,19.0 =F0.05(2,2) 塑性区深度的方差分析结果如表8所示,可以看出,夹矸强度对塑性区发育深度具有一定影响,夹矸厚度与夹矸层位影响显著性较低。 表8 塑性区深度方差分析 巷帮移近量的方差分析结果如表9所示,可以看出,夹矸厚度对巷帮移近量具有一定影响,夹矸强度与夹矸层位影响显著性较低。 表9 巷帮移近量方差分析 方差分析结果与极差分析结果一致,验证了正交试验结果的正确性。 4.2.3 不同煤矸强度比对巷道围岩稳定性影响分析 从以上分析可以看出,夹矸强度、夹矸厚度分别对巷道塑性破坏与巷道围岩变形影响较大。为进一步研究夹矸与煤体共同作用对巷道稳定性影响规律,为此对不同煤矸抗压强度比的掘进工作面巷道围岩稳定性进行试验研究,模拟方案如表10所示。 表10 不同煤矸抗压强度比模拟方案 在夹矸厚度(0.6 m)与夹矸层位(中部)两因素相同条件下,模拟煤矸强度比分别为4∶1、2∶1、1∶1、1∶2、1∶4时巷道变形规律。模型通过固定煤体的黏聚力(煤体单轴抗压强度18 MPa),改变矸石的黏聚力从而改变矸石的单轴抗压强度。不同煤矸强度比时巷道塑性区分布特征如图6所示。 (a)4∶1 (b)2∶1 (c)1∶1 (d)1∶2 (e)1∶4 由图6可以看出,夹矸具有显著的弱面效应。不同煤矸强度比时巷道塑性区深度如图7所示,煤矸强度比分别为4∶1与2∶1时塑性区极其发育,两巷巷道夹矸塑性区深度为1.80 m与1.40 m,其中,煤矸强度比4∶1时塑性区发育最为严重;煤矸强度比为1∶1、1∶2、1∶4时,掘进巷道夹矸塑性区深度为0.2 m,塑性区深度并未发生明显变化。可以看出,夹矸厚度、层位一定时,随着煤矸强度比的减小,夹矸塑性区的深度逐渐减小,特别是在强度比>1时,塑性区深度明显减小;当煤矸强度比<1时,巷道破坏深度较小且塑性区发育深度趋于稳定。 图7 夹矸塑性区深度与煤矸强度比关系 不同煤矸强度比时巷帮移近量如图8所示。由图8可以看出,随着煤矸强度比逐渐减小(夹矸强度逐渐增大),巷道两帮移近量逐渐减小,巷帮移近量同样呈现先快速减小后趋于稳定的趋势;当煤矸强度比小于1∶1时,巷帮移近量最小。 图8 不同煤矸强度比时巷帮移近量 不同煤矸强度比时巷道围岩应力分布规律如图9 所示。当煤矸强度比为4∶1时,巷道围岩应力峰值为10.01 MPa,距离巷道煤壁1.606 m,应力集中系数为1.42;当煤矸强度比为2∶1时,巷道围岩应力峰值为9.82 MPa,距离巷道煤壁1.205 m,应力集中系数为1.39;当煤矸强度比为1∶1、1∶2、1∶4时,巷道围岩应力峰值为9.29 MPa,距离巷道煤壁1.806 m,应力集中系数为1.32。 图9 不同煤矸强度比时围岩支承压力分布规律 应力集中系数、峰值点位置分布规律如图10所示。由图10可以看出,随着煤矸强度比的逐渐减小,巷道围岩应力峰值呈现先快速减小后趋于稳定的趋势,应力峰值位置先靠近巷道煤壁再远离巷道煤壁,应力集中系数逐渐减小,巷道围岩积聚能量减小,有利于巷道围岩稳定性控制。 图10 应力集中系数、峰值点位置分布规律 通过分析不同煤矸强度比时巷道围岩塑性区深度、围岩支承压力分布及巷帮移近量变化规律,可以发现,当含夹矸巷道在煤矸强度比小于1时,巷道最为稳定。现场支护中通过锚杆提高围岩黏聚力从而提高抗压强度,降低夹矸层的塑性深度。分析结果表明,控制煤矸强度比小于1,可以最大程度地降低巷道塑性区破坏和围岩变形。 1)决策树模型结果表明,巷道基本参数对含夹矸巷道围岩变形影响较大,其中埋深影响程度最大;在夹矸因素中,夹矸坚固性系数、夹矸层位及夹矸厚度 3个因素影响权重较大。 2)正交试验结果表明,夹矸强度对巷道围岩塑性区发育深度影响较大,夹矸厚度对巷帮移近量影响较大,其他因素影响较小,影响显著性不高。 3)由直观分析图可知,随夹矸厚度的增加,塑性区发育深度减小趋势不明显,巷帮移近量明显减小;随着夹矸强度的增加,巷道塑性区深度减小趋势最为陡峭;夹矸位于巷道中部位置的围岩稳定性优于巷道上部与下部。 4)通过分析不同煤矸强度比时巷道围岩变形与支承压力分布规律,可以发现,当煤矸强度比小于1时,巷道较为稳定。现场支护中应针对具体地质条件侧重对软弱层进行改性或支护,以此降低煤矸强度比,从而减小巷道围岩变形量。






5 结论

