节理岩体力学参数对双护盾TBM卡机的影响
吴 斐,温 森,b,孔庆梅,b
(河南大学 a.土木建筑学院,b. 河南省轨道交通智能建造工程技术中心,河南 开封 475004)
TBM具有快速、高效、环保、对围岩扰动小等优点被广泛应用于引水隧道、铁路隧道、交通隧道中[1],其在良好地层中施工时,相对于传统的施工方法能缩短工期,如西班牙和摩洛哥之间的直布罗陀海峡隧道[2],奥地利和意大利之间的Brenner基础隧道[3].TBM虽有其他开挖机械难以比拟的优势,但其缺点也很突出,如机身较大不灵活、对复杂地质环境适应性差等特点,使其在不利地质条件中施工较易发生卡机等事故,造成巨大的经济和时间损失,如土耳其Bursa湖南部的Uluabat能源隧道[4],中国台湾北宜高速公路雪山隧道[5],印度Dul Hasti水电工程引水隧洞[6].
大量的TBM卡机报道引起众多学者的关注,并进行相关的研究后指出:岩体和护盾之间的相互作用是卡机的主要原因[7-9],所以预防卡机研究的重点是TBM开挖后围岩的力学响应.目前研究岩体力学响应的方法主要有室内相似实验和数值模拟,每一种方法都有其利弊,室内相似实验可以采用工程原状岩体或利用类岩石材料浇筑岩体进行,其能够尽可能地还原岩体本身的力学特性,是一种行之有效的办法.如Yang等[10-11]利用类岩石材料浇筑复合岩层,研究在深埋复合地层中开挖圆形隧道后围岩的应力、变形、破坏的演化和重分布.但是由于室内相似实验需要的试块具有不可重复性和造价高等特点,使得该方法的推广受到限制.
随着计算机和各种数值模拟软件的迅猛发展,众多学者利用有限元软件进行均质岩体的数值模拟,但随着深埋长大隧道的建设,所遇到的岩体基本都含有断层、节理、层理等不连续面,且围岩的破坏大多与不连续面有关[12],有限元软件并不能很好的模拟存在不连续面的岩体,而离散元作为一种专门解决不连续介质问题的方法,可以弥补此缺陷.因此文献[13-17]使用离散元软件建模分别研究了层理和节理的倾角、间距以及隧道尺寸、埋深对围岩稳定性的影响.此外,还有学者利用有限差分法软件进行了研究.如:文献[18-20]利用有限差分法软件建立模型,分析了隧道开挖后围岩的变形,以及变形后与护盾的接触和TBM卡机机理.陈虎等[21]采用FLAC3D研究不同开挖断面形式对LDP曲线的影响.Hasanpour等[22-26]为了避免卡机而研究岩体、护盾、衬砌和回填材料之间的相互作用,考虑护盾锥度构造并利用FLAC3D建立完整的三维模型,通过提取围岩上各点的信息来绘制LDP和LFP曲线来研究扩挖间隙、施工速度、GSI、弹性模量、隧道半径,护盾长度等参数对TBM卡机的影响.
综上而言,目前对于节理岩体的研究大多都集中于节理的倾角、走向、间距、埋深等对围岩稳定性的影响,考虑节理岩体力学参数对围岩与TBM接触压力影响的文献鲜有报道.本文作者基于三维离散元软件和正交试验设计,定量研究岩体力学参数对围岩与TBM接触压力的影响.
1 数值模型建立及正交试验
1.1 模型建立
隧道处于节理岩体中,自重应力为26.5 MPa,侧压系数为1,节理间距为3 m,节理倾角和节理走向与隧道轴线夹角均为45°,模型尺寸X(垂直于TBM掘进方向)、Y(TBM掘进方向)、Z(竖直方向)分别为:140 m、100 m、140 m,节理岩体模型如图1所示.根据文献[27]建立TBM模型,建模时考虑了护盾偏心设计的影响,由此导致前后盾与围岩接触间隙不均匀.护盾顶部与围岩间隙为t最大,底部与围岩间隙为t最小,护盾与围岩位置关系如图2(a)所示,TBM详细几何参数如图2(b)所示.
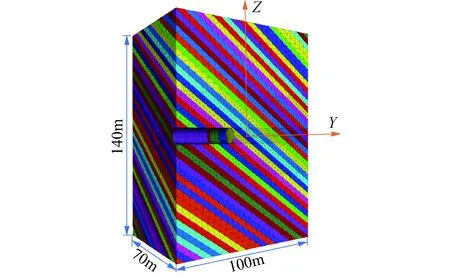
图1 节理岩体模型Fig.1 Jointed rock mass model
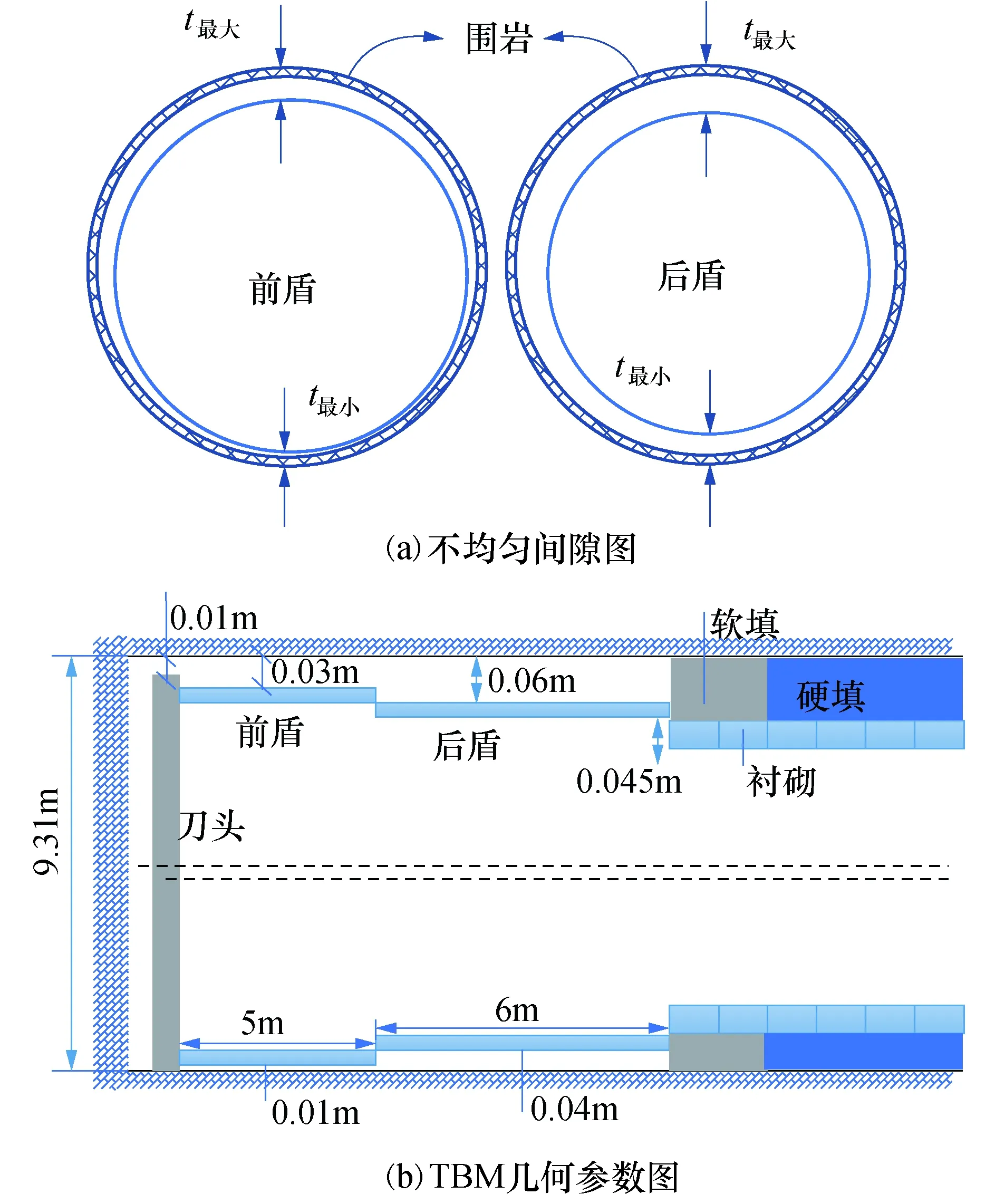
图2 双护盾TBM图Fig.2 Schematic diagram of double-shield TBM
1.2 正交试验设计
1.2.1 原理
所谓正交试验[28],是一种处理多因素试验的科学方法,利用设计好的规格化正交表安排试验可以减少工作量的同时仍保证结果的可靠性.如7因素2水平试验,全面试验需27=128次,利用正交试验则进行8次即可,并使用极差和方差对试验结果进行分析,得到不同因素的显著性排序.
1.2.2 正交试验步骤
正交试验设计包括两方面:一是试验设计,二是数据处理.在试验设计时选取因素并不是越多越好,而是要根据具体研究内容和经验进行分析,选出主要因素,略去次要因素,以免加大无效工作量[28],具体试验步骤见图3.图3中,K为不同因素下各水平试验结果之和,R为极差.
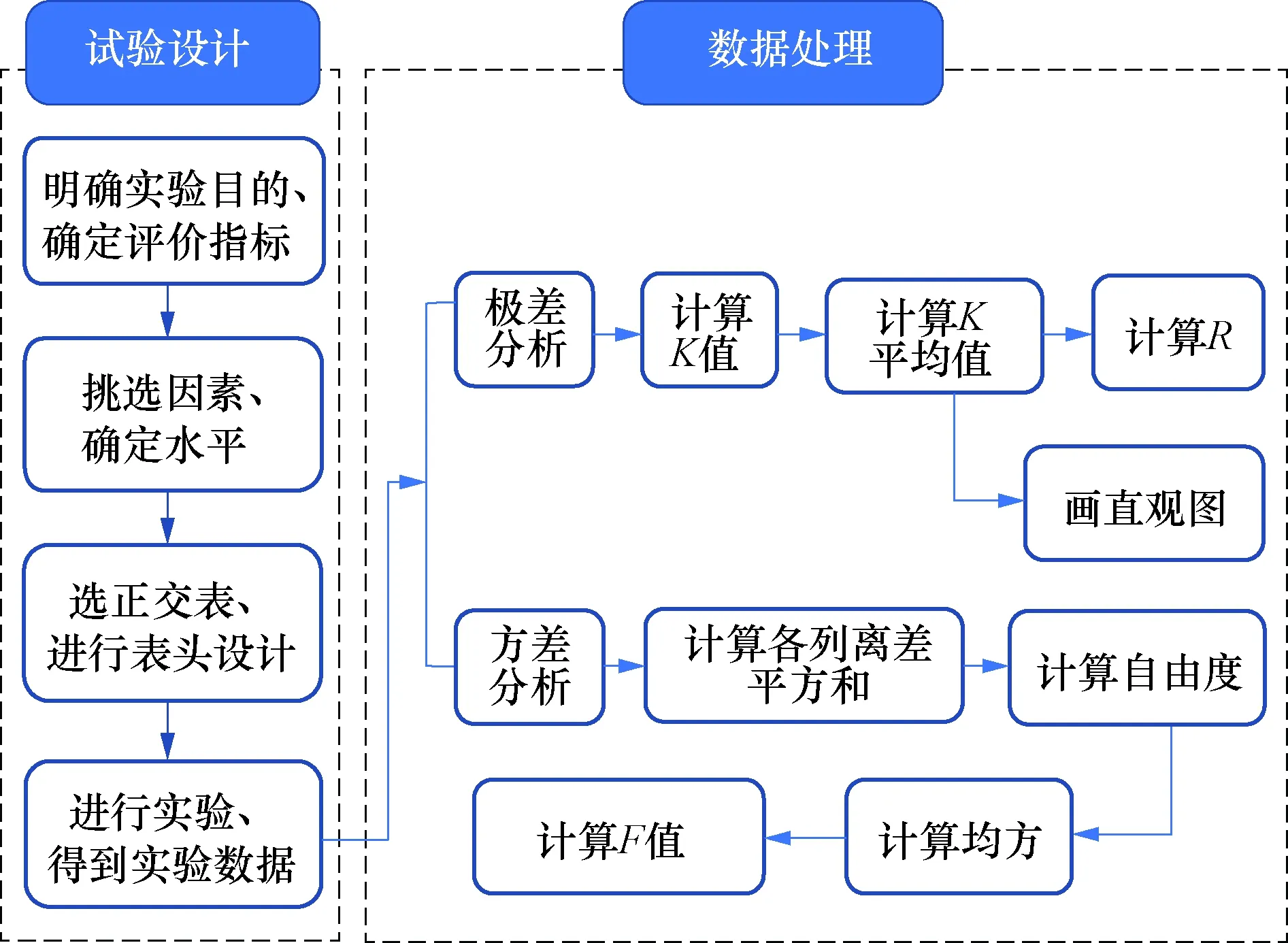
图3 正交试验设计步骤图Fig.3 Design diagram of orthogonal test
2 不同参数对接触压力的影响
2.1 试验因素及水平
岩体变形由岩石变形和节理变形共同组成,由于岩石和节理的力学参数对岩体变形影响显著性不同,为了分析不同参数对岩体变形的影响,选取岩石参数(弹性模量E、泊松比μ、黏聚力c、内摩擦角φ)和节理参数(法向刚度kn、剪切刚度ks、节理黏聚力jc、节理内摩擦角jφ)为因素进行正交试验设计,每个因素选取5个水平,各水平取值主要考虑到TBM掘进岩石的抗压强度一般为30~150 MPa,同时参考了工程中常见的岩石、节理力学参数[29-32],具体因素和水平见表1.
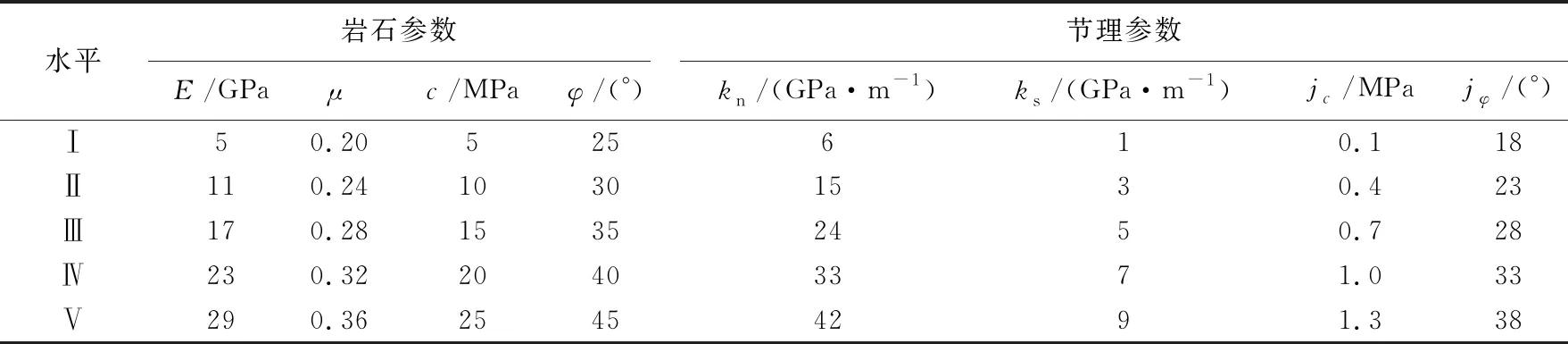
表1 岩石、节理力学参数水平取值
2.2 方案设计
选取L50(59)(下标50代表试验次数为50次,5表示试验水平,9表示试验因素)正交设计表,通过离散元软件3DEC对每组试验进行数值模拟计算并提取围岩与TBM的接触压力Q,试验选取8因素5水平,但方差分析时需有一空列作为D列(误差列),所以选取9因素5水平正交表.
围岩与TBM接触压力Q的提取,考虑护盾锥度的影响,因此围岩与护盾的接触压力沿护盾轴线方向分布不均匀,故应该对护盾上的微小面积进行积分,转化为曲面积分问题,护盾上微小面积所受压力pi(y,z)为[7]
(1)
式中:ur(y,z)为围岩位移;ur(0)为开挖面前方预变形量;ψi=ψi(y,z)为第i节护盾与围岩之间的不均匀间隙,Ks为护盾刚度.
护盾总压力Q为
(2)
式中:Wa为围岩施加在第a节护盾上的压力.
根据式(1)、式(2)提取围岩与护盾接触压力Q,结果见表2.
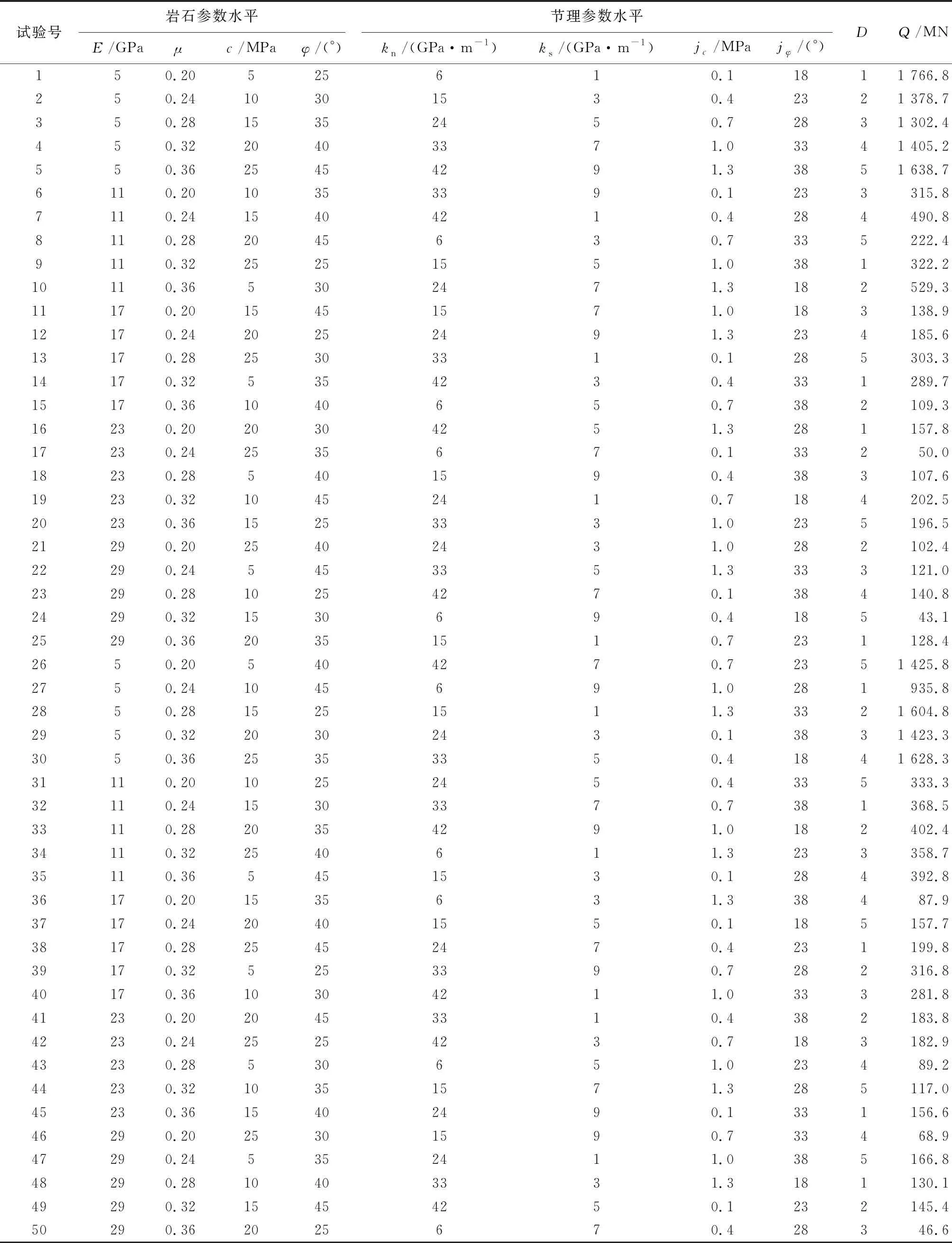
表2 岩石、节理力学参数正交设计表
2.3 结果分析
为了判断试验指标随各因素水平变化的趋势和各因素对试验指标影响的显著性,进行极差[28]和方差分析.
2.3.1 极差分析
不同因素下各水平的试验结果之和Kij为
Kij=∑Qi
(3)
式中:i为试验水平(1≤i≤5);j为试验因素(1≤j≤9).
(4)
式中:s为任一列上各水平出现的次数.
各因素的极差Rj为
(5)
按照式(3)~式(5)计算各因素的Kij、¯Kij和Rj,结果见表3,比较各因素极差Rj的大小,极差越大表示该因素变化时对试验结果影响越大.
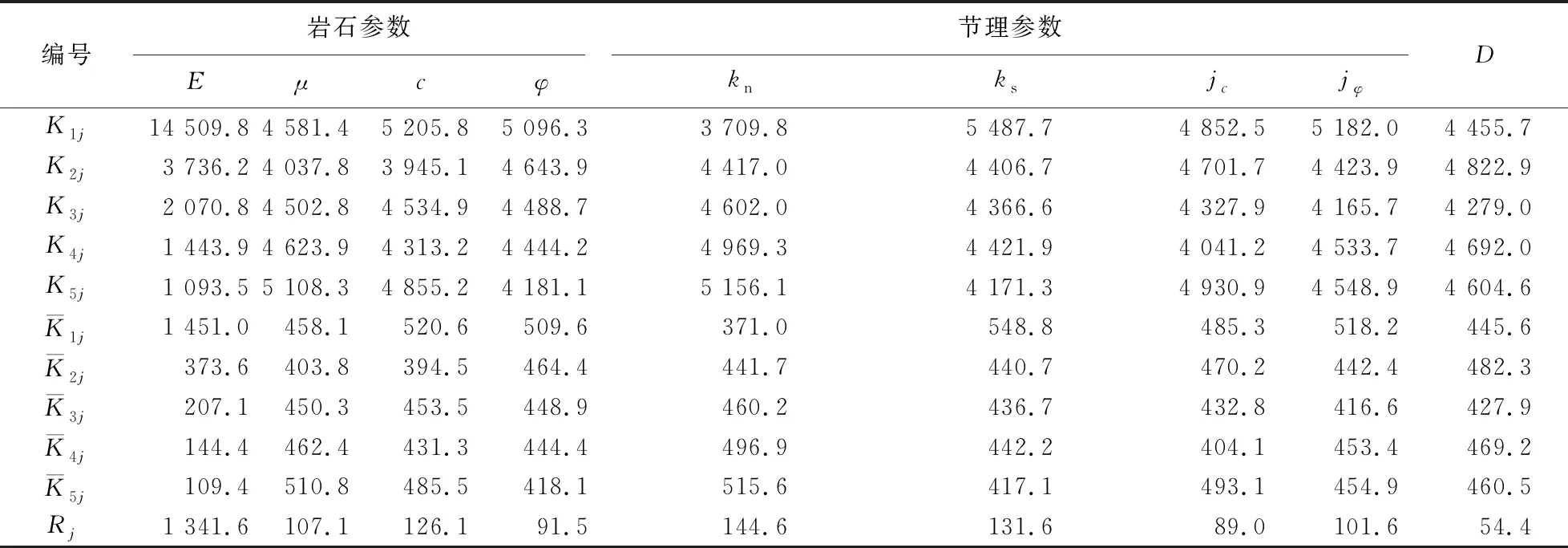
表3 岩石、节理力学参数极差分析表
由表3可知:以围岩与护盾接触压力Q为评价指标的各因素极差影响程度由大到小排序为:弹性模量、法向刚度、剪切刚度、黏聚力、泊松比、节理内摩擦角、内摩擦角、节理黏聚力.弹性模量极差远大于其他参数,故其对Q影响最大,节理黏聚力极差最小,故对Q影响最小.
为了更加直观地判断各因素对接触压力的影响大小,以因素为横坐标,实验指标Q的平均值为纵坐标,绘制关系曲线,如图4所示.
由图4可知:接触压力随着弹性模量、黏聚力、内摩擦角、节理内摩擦角、剪切刚度的增大而减小,其中岩石弹性模量对Q影响最大,弹性模量从5 GPa增加到11 Gpa,围岩与TBM的接触压力急剧减小,减小了74.3%;从11 GPa增加到29 Gpa,接触压力持续减少,但幅度相对较小,减小了70.7%,这是因为弹性模量是反映岩石变形的主要参数,弹性模量增加,岩石的抗变形能力增大,因此围岩与TBM接触压力减小.接触压力随着节理剪切刚度从1 GPa·m-1增加到9 GPa·m-1,Q从548.8 MN减小到417.1 MN,减小了23.9%,这是因为剪切刚度的增加使得节理面抗剪强度提高.接触压力随着黏聚力、内摩擦角、节理内摩擦角的增大均减小,但幅度相对较小.
接触压力Q随着泊松比和法向刚度的增大而增大,当节理法向刚度从6 GPa·m-1增加到42 GPa·m-1,接触压力从371 MN增加到515.6 MN,增加了39%,此结论与文献[33]研究结论一致.随着泊松比从0.2增加到0.36,Q从458.1 MN增加到510.8 MN,增加11.5%.
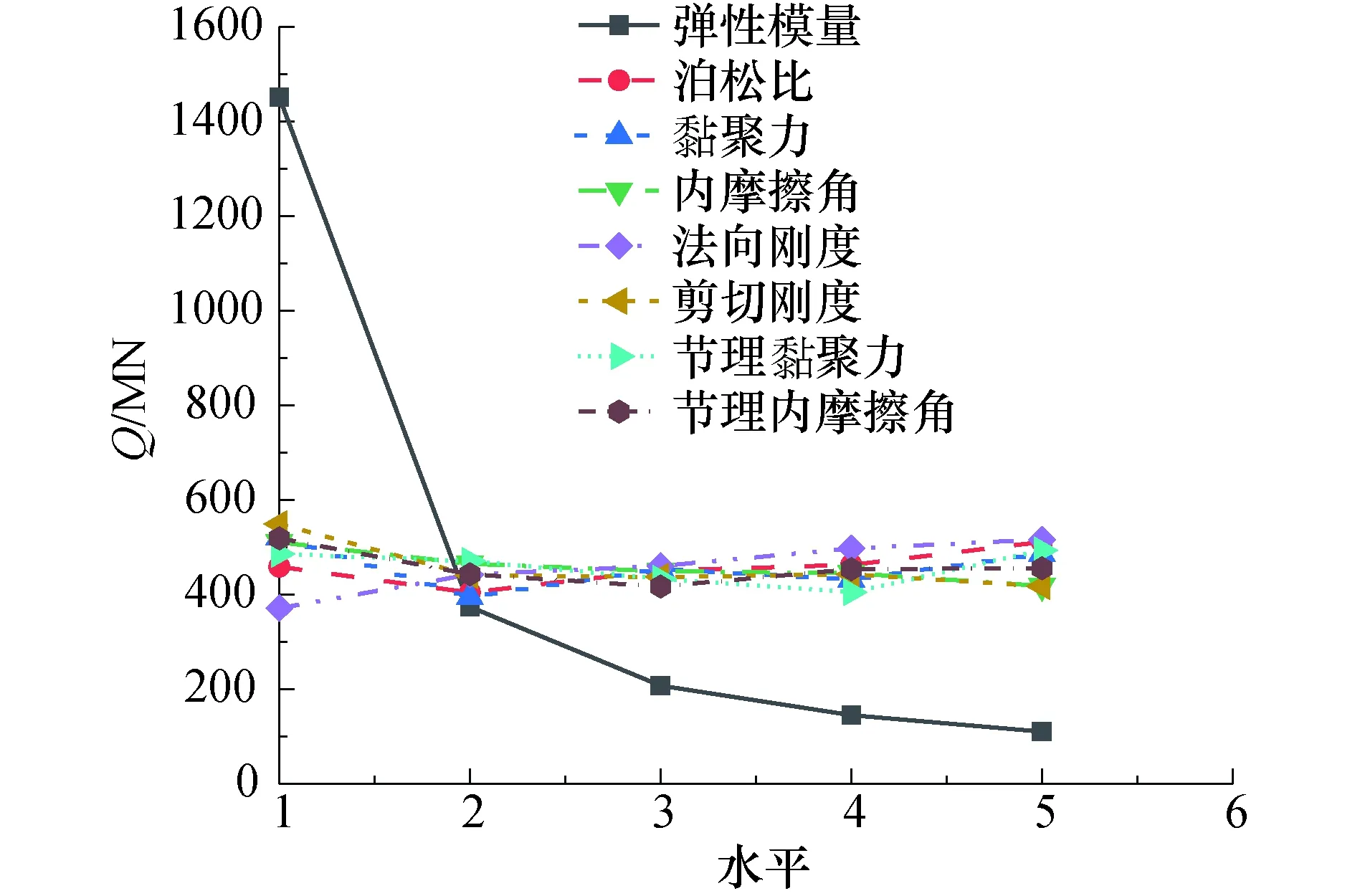
图4 接触力随水平变化曲线Fig.4 Curves of contact force changing with level
2.3.2 方差分析
由极差分析可得各因素对试验指标影响的大小,但是极差分析不能估计误差的大小,不能精确估计各因素对试验结果影响的显著程度.方差分析可以将试验结果的波动分解为因素水平变化引起的波动和试验误差引起的波动,并进行比较,得出各因素对试验指标影响的显著性排序,可弥补极差的不足.
方差详细计算步骤如下[28]:
总的离差平方和SST为
(6)
式中:n为总的试验次数(n=50);m为试验编号;Qm为不同编号下围岩与TBM接触压力.
各因素引起的离差平方和SSj为
(7)
式中:r为水平数(r=5).
因此总的离差平方和等于每一列离差平方和的和,其表达式为
(8)
表2中将第9列作为误差列,故当j=9时,根据式(7)计算出的结果为误差列的离差平方和SSD.
误差总的离差平方和SSe等于所有误差列离差平方和SSD的和,其表达式为
SSe=∑SSD
(9)
总的自由度dfT、每一列对应的自由度dfj表达式分别为
dfT=n-1
(10)
dfj=i-1
(11)
式(11)中,当j=9时,计算出的结果为误差列对应的自由度dfD,故误差列对应总的自由度dfe为所有误差列自由度dfD的和,dfe表达式为
dfe=∑dfD
(12)
不同因素的均方MSj为
(13)
误差的均方MSe为
(14)
不同因素的F值计算表达式为
(15)
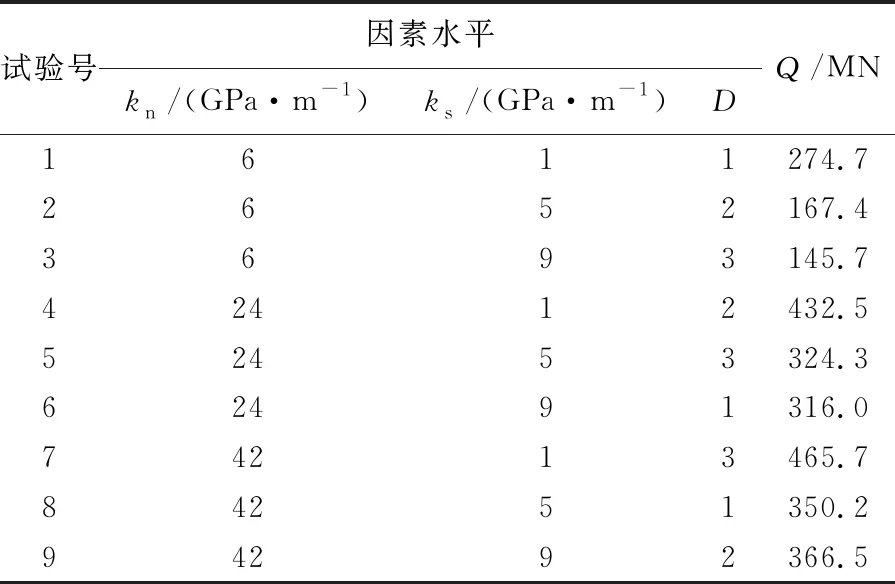
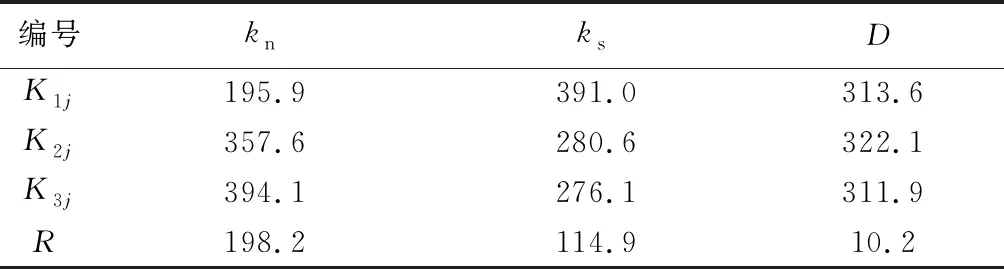
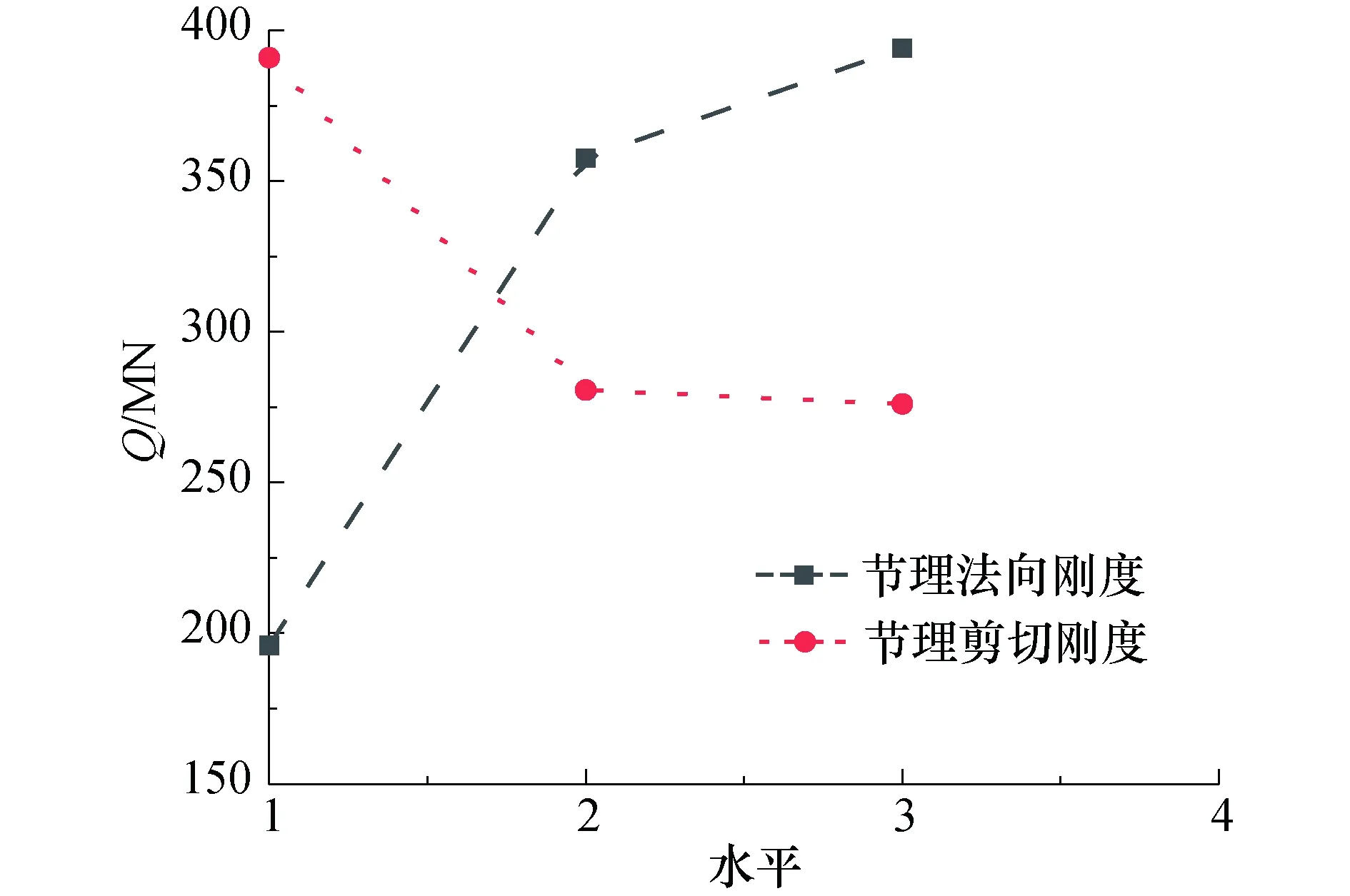
根据式(6)~式(15)计算不同因素的F值,并根据文献[28]得Fa(dfj,dfe)在dfj和dfe均为4时,a=0.01、0.05、0.1和0.25的值分别为:F0.01(4,4) = 15.977、F0.05(4,4) = 6.388、F0.1(4,4) = 4.107、F0.25(4,4) = 2.064,最后将不同因素的F值与Fa(dfj,dfe)相比较,若F>F0.01(4,4),则表明该因素影响极其显著,F0.05(4,4) 表4 岩石、节理力学参数方差分析表 由表4可知:弹性模量的F值远大于F0.01(4,4),故弹性模量对围岩与TBM接触压力影响极其显著,法向刚度的F值介于F0.01(4,4)和F0.05(4,4)之间,故其对接触压力的影响仅次于弹性模量,为非常显著.黏聚力和剪切刚度的F值介于F0.1(4,4)和F0.05(4,4)之间,故其对接触压力有显著影响,泊松比、内摩擦角、节理黏聚力和节理内摩擦角的F值仅大于F0.25(4,4),故其对接触压力仅是有影响. 当节理倾角为45°时,根据2.3节得到节理法向刚度显著性大于节理剪切刚度,但节理两侧岩体随着节理倾角增大更容易产生剪切滑移破坏,因此需进一步分析当节理倾角增大甚至接近90°时,节理法向刚度和剪切刚度对围岩与TBM接触压力影响的显著性.选取法向刚度和剪切刚度为因素,选用3因素3水平正交表,具体因素和水平取值见表5.按照式(1)~式(2)计算围岩与TBM接触压力Q,见表6. 表5 参数水平取值 表6 正交设计表 按照式(3)~式(5)计算节理法向刚度和剪切刚度的R值并列于表7中. 表7 极差分析表 由表7可知:法向刚度的极差大于剪切刚度,故其对围岩与TBM接触压力的影响仍大于剪切刚度. 为了更加直观地判断节理法向刚度和剪切刚度对接触压力的影响,以因素为横坐标,实验指标平均值为纵坐标绘制关系曲线,如图5所示. 图5 接触力随水平变化曲线Fig.5 Curves of contact force changing with level 由图5可知:法向刚度从6 GPa·m-1增加到42 GPa·m-1时,接触压力从195.9 MN增加到394.1 MN,增加了101.2%;剪切刚度从1 GPa·m-1增加到9 GPa·m-1时,接触压力从391 MN减小到276.1 MN,减小了29.4%,故法向刚度影响更大. 按照式(6)~式(15)计算节理法向刚度和剪切刚度的F值,并根据文献[28]得Fa(dfj,dfe)在dfj和dfe均为2时,a=0.01、0.05、0.1和0.25的值分别为:F0.01(2,2) = 99、F0.05(2,2) = 19、F0.1(2,2) = 9、F0.25(2,2) = 3,然后将节理法向刚度和剪切刚度F值与Fa(dfj,dfe)相比较,结果如表8所示. 表8 方差分析表 由表8可知:法向刚度和剪切刚度对围岩与TBM接触压力影响均显著,但由于法向刚度F值与F0.01(2,2)的差远大于剪切刚度的F值与F0.01(2,2)的差,故法向刚度比剪切刚度影响更显著,与2.3节结论一致. 以正峰寺隧道[34]为依托,其进口位于四川省古蔺县石屏乡,洞身段处于古蔺县自强乡,出口位于古蔺县东兴乡,所处地貌主要为侵蚀地貌,沟谷发达,地形高程起伏较大,山体相对高程差达300 m.选取其里程桩号DK78+239处为研究对象,该处掌子面较为完整,岩性为奥陶系下统湄潭组辉绿色页岩,重度γ为21 kN/m3,薄-中厚构造,厚度为10~50 mm,倾向为305°,倾角为8°.掌子面素描图如图6[34]所示. 图6 掌子面素描图Fig.6 Sketch of palm surface 3.2.1 模型建立 根据正峰寺隧道地质勘察报告建立数值模型,按照隧道面积相等原则将截面面积为63.7 m2马蹄形隧道转换为隧道断面直径为9.01 m圆形隧道,模型边界选取为42 m×42 m×42 m(长×宽×高),模型内均匀分布一组节理,间距为0.5 m,倾向为305°,倾角为8°,隧道埋深为180 m,模型如图7所示,岩石和节理具体参数如表9所示[34],表9中,σt为节理抗拉强度. 图7 算例模型图Fig.7 Case model diagram 在节理岩体中采用TBM施工时,通常会采取一些措施来预防卡机,虽然弹性模量对围岩与TBM接触压力影响较大,但在施工中提高岩石弹性模量较为困难.所以目前采用较多的方法是通过打锚杆、注浆等手段增大节理参数来预防卡机,因此选取节理参数对正峰寺隧道进行研究. 3.2.2 结果分析 采用单因素分析法,即一次只改变一个参数,其他参数不变,分析可得到该参数改变对结果的影响.将kn、ks、jc、jφ增加30%后分别表示为kn30、ks30、jc30、jφ30.例如:根据地质勘探报告知节理法向刚度kn为10 GPa·m-1,利用单因素分析法仅将节理法向刚度增加30%后kn30为13 GPa·m-1,根据式(1)~式(2)计算并提取Q可知,法向刚度增加30%后,围岩与TBM接触压力由42.3 MN增大到46.9 MN,增加了10.9%,同理,节理剪切刚度、节理内摩擦角和节理黏聚力分别增加30%后,围岩与TBM接触压力变化了3.1%、0.7%、0.7%.节理参数改变对围岩与TBM接触压力Q的影响见表10. 表9 岩体参数表 表10 节理参数计算结果 由表10可知:节理参数中法向刚度对接触压力影响最大,法向刚度增加30%后,围岩与TBM接触压力增加了10.9%;其次为剪切刚度,剪切刚度增加30%后,接触压力减小3.1%,节理内摩擦角和黏聚力均对结果影响相对较小. 1)将正交试验和离散元软件相结合,定量分析了节理岩体力学参数对围岩与TBM接触压力的影响.结果表明,在层状节理岩体隧道中,岩体参数对围岩与TBM接触压力影响的显著性排序由大到小为:弹性模量、法向刚度、剪切刚度、黏聚力、泊松比、节理内摩擦角、内摩擦角、节理黏聚力. 2)岩石参数中,弹性模量影响极其显著,因此在施工中要考虑适当封堵地下水,防止其对岩石软化导致弹性模量降低,从而对施工造成不利影响.同时由于实际工程中很难提高岩石参数,所以在选线和施工时应该注意岩石参数的影响. 3) 节理参数中影响较显著的因素是法向刚度和剪切刚度,但由于法向刚度增大会导致接触压力增大,所以在采用注浆等手段时应该考虑其对法向刚度的影响.可以通过打锚杆等措施增大节理的抗剪强度,从而减小围岩与TBM的接触压力,减少卡机事故.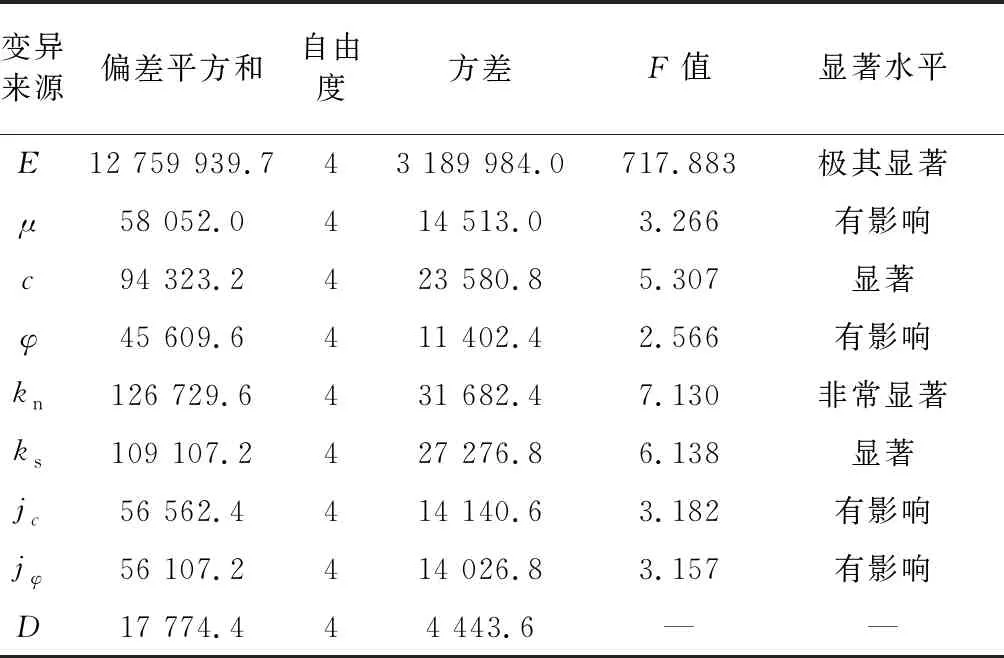
2.4 验证分析


3 算例分析
3.1 工程概况

3.2 数值模型及结果分析



4 结论

