近十年高考数学全国卷“平面向量”试题分析及教学思考*
项丽红 逯彦周
(甘肃省永登县第六中学 730300)
向量理论具有深刻的数学内涵和丰富的物理背景.向量具有几何与代数双重属性,是沟通几何与代数的桥梁,同时高中的平面向量知识是进一步学习高等数学的基础.2012年—2021年十年间,我国高考数学命题经历了考试大纲、课程标准并存指导,到终止考试大纲,完全依据课程标准的过程.对这十年高考数学全国卷中的平面向量试题在宏观层面从类型、题数、分值、难易程度进行统计分析,在微观层面从试题考查知识点、融合其他知识点进行统计分析,并以此为依据对教师教学提出一些建议.
1 十年高考全国卷平面向量试题宏观统计分析
以2012—2021十年高考全国卷(共29套)中的平面向量试题(共38道)为研究对象,将38道平面向量试题从宏观层面按类型、题数、分值、难易程度进行统计,结果如表1所示.从类型看,38道题目中,选择题共20道,填空题共14道,解答题共4道,占比分别为52.6%、36.9%、10.5%.从题数看,29套试卷中,21套试卷的平面向量试题均为1道,占比72.4%,分值为5分;4套试卷的平面向量试题均为2道,占比13.8%,分值为10分;3套试卷的平面向量试题均为2道,占比10.3%,分值为17分;仅有1套试卷中平面向量试题为3道,分值为22分.从难易程度看,38道试题中,难度为易、中的试题分别为20道、12道,占比分别为52.6%、31.6%,较难题为6道,占比15.8%.
表1 2012—2021全国卷平面向量试题统计
年份卷别选择题填空题解答题题目数量分值易中难2012全国大纲卷1151新课标卷11512013全国大纲卷221011新课标Ⅰ卷1151新课标Ⅱ卷11512014全国大纲卷1151新课标Ⅰ卷112102新课标Ⅱ卷11512015新课标Ⅰ卷221011新课标Ⅱ卷11512016新课标Ⅰ卷1151新课标Ⅱ卷1151新课标Ⅲ卷1151
续表
年份卷别选择题填空题解答题题目数量分值易中难2017新课标Ⅰ卷1151新课标Ⅱ卷112172新课标Ⅲ卷11512018新课标Ⅰ卷22102新课标Ⅱ卷1151新课标Ⅲ卷11217112019新课标Ⅰ卷11132212新课标Ⅱ卷1151新课标Ⅲ卷11512020新课标Ⅰ卷1121711新课标Ⅱ卷1151新课标Ⅲ卷11512021全国甲卷1151全国乙卷1151新高考Ⅰ卷1151新高考Ⅱ卷1151
2 十年高考全国卷平面向量试题微观知识点分析
2.1 试题考查知识点统计分析
将平面向量试题考查知识点按照线性运算及其几何意义、向量平行、平面向量基本定理、平面向量的数量积及模与夹角、向量垂直、平面向量坐标运算进行统计(只要试题有体现就计数),结果如表2所示.由表2知,38道试题中,考查线性运算及其几何意义、平行、垂直、平面向量基本定理、数量积及模与夹角的试题分别有5道、4道、5道、4道、14道,占比分别为13.2%、10.5%、13.2%、10.5%、36.8%;考查线性运算、平行、垂直、数量积及模与夹角的坐标运算的试题分别有10道、4道、6道、17道,占比分别为26.3%、10.5%、15.8%、44.7%.总的来看,考查线性运算、平行、垂直、数量积及模与夹角的分别有15道、8道、11道、31道,占比分别为39.5%、21.0%、29.0%、81.5%.
表2 2012—2021全国卷平面向量试题考查知识点统计
知识点线性运算及其几何意义平行基本定理数量积、模、夹角垂直坐标运算线性平行数量积、模、夹角垂直考查题数544145104176
在38道平面向量试题中,28道只考查了平面向量内容的知识点,没有与其他知识融合,且绝大多数试题考查知识单一,属于简单题.如:
例1
(2021年全国甲卷第14题)已知向量=(3,1),=(1,0),=+k
.若⊥,则k
=.
分析 本题考查平面向量的坐标运算,平面向量垂直的条件,属于基础题.易求得
例2
(2017年全国Ⅰ卷第13题)已知向量,的夹角为60°,||=2,||=1,则|+2|=.分析 本题考查平面向量数量积的计算.代数法:|+2|=||+4·+4||=4+4×2×1×cos 60°+4=12,故几何法:利用如下图形(图1),可以判断出+2的模长是以2为边长,一个角为60°的菱形的较长对角线的长度,则为
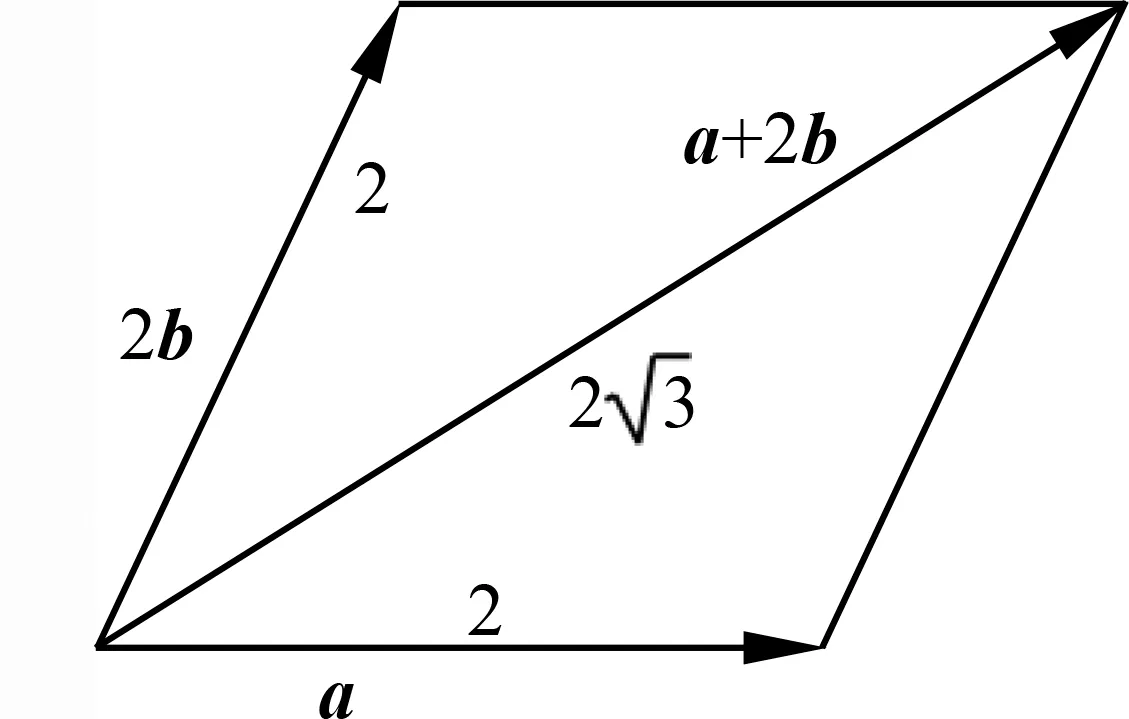
图1
2.2 试题融合其他知识点统计分析
平面向量与其他知识点的融合具有明显的倾向性(表3),38道平面向量试题中,10道融合了其他知识,其中与圆锥曲线的融合包括圆、椭圆、双曲线与抛物线,共有6道,其余4道是与三角函数及解三角形、函数、数列融合.
表3 2012—2021全国卷平面向量试题交汇知识统计
交汇知识圆锥曲线圆椭圆双曲线抛物线三角函数及解三角形函数数列考查题数1212211
当平面向量试题融合其他知识时,多考查平面向量的坐标运算,多数为数量积及模与夹角、垂直的坐标运算.如:
例3
(2021年新高考Ⅱ卷第10题)已知O
为坐标原点,点P
(cosα
,sinα
),P
(cosβ
,-sinβ
),P
(cos(α
+β
),sin(α
+β
)),A
(1,0),则( )分析 本题情境熟悉,是知识交汇题,主要考查平面向量的模、数量积运算以及三角恒等变换,难度中等.通过计算可知故A,C正确.
例4
(2018年全国Ⅲ卷第20题)已知斜率为k
的直线l
与椭圆交于A
,B
两点,线段AB
的中点为M
(1,m
)(m
>0).(1)证明:
(2)设F
为C
的右焦点,P
为C
上一点,且证明:成等差数列,并求该数列的公差.分析 本题主要考查直线与椭圆的位置关系,等差数列的性质以及平面向量的坐标运算,重点考查数学抽象、逻辑推理、数学运算素养以及函数与方程、转化与化归的数学思想方法.(1)设而不求,利用点差法进行证明;(2)解出m
,进而求出点P
的坐标,得到再由两点间距离公式表示出得到直线l
的方程,联立直线与椭圆方程用韦达定理进行求解.解
(1)设A
(x
,y
),B
(x
,y
),则两式相减,并由得
由题意知于是①
由题意得故
(2)由题意得F
(1,0),设P
(x
,y
),则(x
-1,y
)+(x
-1,y
)+(x
-1,y
)=(0,0).由(1)及题设得x
=3-(x
+x
)=1,y
=-(y
+y
)=-2m
<0.又因为点P
在C
上,所以从而于是同理
所以
故即成等差数列.
设该数列的公差为d
,则②将代入①得k
=-1.所以l
的方程为代入C
的方程,并整理得故代入②解得所以该数列的公差为或
3 研究结论与教学建议
3.1 研究结论
近十年高考数学全国卷平面向量试题近九成是选择题和填空题,且选择题居多,超七成试卷只有1道平面向量试题,分值5分,超两成试卷有2道平面向量试题,分值为10分与17分(二者数量相差不大),题目难度以易、中为主,占比和超八成,以知识融合题为主的难题占比低于两成.平面向量试题考查知识点按比例由高至低依次为数量积及模与夹角、线性运算及其几何意义、垂直、平行、平面向量基本定理,且对坐标运算的考查多于非坐标运算的考查.平面向量与其他知识的融合主要集中在圆锥曲线、三角函数与解三角形、函数、数列等.
3.2 教学建议
3
.2
.1
理解概念,牢记公式,稳固双基教材对于平面向量内容多是按照基本概念→线性运算及其几何意义→平面向量基本定理→坐标运算→平面向量数量积的顺序编排,基本概念是后续知识展开的基础,特别是平面向量基本定理,是坐标运算的“根”,坐标运算是其“果”.这部分知识前面概念多,后面公式多,但就全国卷而言考查内容简单,多为选择题和填空题,考查内容基本为数量积及模与夹角、线性运算及其几何意义、垂直、平行、平面向量基本定理的简单应用,有坐标运算,也有非坐标运算.因此在教学中须让学生切实理解概念,记牢公式,稳固双基.
3
.2
.2
画好图形,精准运算,数形结合平面向量兼具几何与代数双重属性,教材安排也是先“几何”后“代数”的顺序,并且线性运算以及数量积运算都有丰富的物理背景,是学科交叉的良好案例.对于高中生而言,平面向量也是数形结合的良好案例.因此,在日常教学中,教师要注重学生画图习惯的养成,画对图,画好图,为之后的数学运算当好“眼睛”,在此过程中亦能培养数学抽象、直观想象、逻辑推理及数学运算素养.
3
.2
.3
总结反思,建构体系,提升素养在平面向量与其他知识的融合中,可以发现平面向量充当辅助工具的作用,且这类题目往往对平面向量知识的考查多在坐标运算上,也很简单,重点在于与其他知识融汇贯通,这就需要建构知识体系.高中数学知识点多,抽象程度也较高,但是好在知识之间彼此是相通的,所以我们的学习不会因所学知识的增多而负担增重,反而会因发现、理解先后知识的联系而叹为观止.因此,在教学中要注重引导学生对知识的梳理、总结、反思,总结的次数多了,学生就会发现知识间的联系,找到联系、及时反思,就能自主建构属于自己的“知识体系”,当然在此过程中也可提升数学核心素养.

