温度对铁路桥梁刚度性能的影响分析
孟浩伟
(中铁十九局集团华东工程有限公司,浙江 宁波 315400)
随着高铁技术的飞速发展,我国已经成为世界上重要的铁路里程大国和铁路技术输出大国。在大量的工程实践中,我国积累了铁路建设相关经验。从已有的经验和研究成果来看,铁路桥梁是铁路建设和后期运营中非常重要的环节,对铁路运输效率的提升和铁路系统稳定可靠地工作具有十分重要的意义[1]。从各种统计数据来看,温度、湿度、沉降和结构性因素是影响铁路桥梁安全稳定运营的四大因素。而和其他三类因素相比,温度因素产生了更明显的影响,甚至超过因建筑材料等导致的铁路桥梁结构性问题[2]。因此,针对温度因素对铁路桥梁影响的研究日益增多,其主要研究思路是在考虑温度参数的前提下建立铁路桥梁的刚度参数变化模型[3]。在此类研究中,先后出现了温度参数和铁路桥梁振动频率的相关模型、温度参数和铁路桥梁建筑材料弹性模量的相关模型、温度参数和铁路桥梁刚度的希尔伯特变换模型、温度参数与铁路桥梁刚度关系的贝叶斯模型等。该文将分析铁路桥梁振动效应的变化规律,进而构建温度参数和铁路桥梁刚度之间的关系模型,并通过试验考察温度对铁路桥梁刚度性能的影响。
1 铁路桥梁刚度性能的采集
为了准确把握铁路桥梁的工作状态和稳定情况,需要重点监测铁路桥梁的刚度性能参数。在各种刚度性能参数中,振动频率虽然不是最直接的可以测量的刚度参数,但却是反应铁路桥梁性能最好的刚度性能参数。为了获得铁路桥梁的刚度性能参数,人们建立了基于结构模型的振动频率响应函数、基于结构模型的振动频率响应函数,都可以获得铁路桥梁的振动频率。在这些测量方式中,需要通过施加特定的输入刺激才能进行振动频率的测量。这里又可以分为两大类刺激手段:一类是利用铁路桥梁工作环境中的自然激励,如将一些不平稳的并且具有非线性特征的信号作为输入,观察铁路桥梁振动情况的变化。另一类是通过人工激励,将给定的一些人工调制的信号作为输入刺激,观察铁路桥梁振动情况的变化。相比较而言,环境激励的实现有一定局限性,人工激励则可以最大限度地按照测试设计者的要求给出输入刺激。因此,这里采用希尔伯特变换法进行人工激励,以实现对铁路桥梁振动频率的测量。
基于希尔伯特变换完成铁路桥梁振动频率测量的流程,如图1所示。
如图1所示,采用希尔伯特变换获取铁路桥梁振动频率的第一步就是采集铁路桥梁振动信号,主要方法是采用基于白噪声的概率统计方法,其核心公式如公式(1)和公式(2)所示。

图1 基于希尔伯特变换的铁路桥梁振动频率测量
式中:σo为包括铁路桥梁振动信号的原始信号的标准差;σn为考虑白噪声的原始信号的标准差;α为第一比值参数。
式中:σo为包括铁路桥梁振动信号的原始信号的标准差;σh为原始信号低频以上部分信号的标准差;ε为第二比值参数。
当第二比值参数大于第一比值参数的3倍时,可以确定求解铁路桥梁振动频率的模态函数并准确捕获其衰减响应,进一步根据希尔伯特变换计算出铁路桥梁的振动频率,如公式(3)所示。
式中:ωd为铁路桥梁振动过程中的阻尼频率;ω0为铁路桥梁的振动频率;ξ2为铁路桥梁振动过程中的阻尼比。
至此,就可以采用希尔伯特变换计算出铁路桥梁的振动频率。
2 温度对铁路桥梁刚度性能的影响模型
如前所述,该文选择将振动频率作为铁路桥梁刚度的表征参数,并根据希尔伯特变换的方法实现了铁路强梁振动频率参数的采集。接下来的工作就是分析温度对铁路桥梁刚度的影响,即温度对振动频率的影响,其关键在于构建从温度到振动频率之间的关系模型。
对多参数之间变化对应关系的分析和理解过程中,贝叶斯估计从先验概率和后验概率的角度出发,获得过很大的成功,成为理论上非常有效的分析方法。但是,对很多实际问题而言,贝叶斯估计既无法提供准确的先验概率,也无法事先得知后验概率,从而使贝叶斯估计无法在实际中运用和实施。对铁路桥梁刚度性能和温度之间的关系,贝叶斯估计也无法在实际中有效地构建出估计模型。
ABC方法认为,贝叶斯估计如果无法提供充分的先验概率和后验概率条件,就会导致估计模型难以构建或者估计过程的最大似然函数难于求解。因此,ABC方法找到了一种解决思路,只需要先验概率的一部分样本就可以替代原来的全部先验概率数据,并且可以通过先验概率样本逼近出近似的后验概率分布。这其中的关键在于先验概率样本数据和观测数据的有效比对,尤其是比对过程要充分满足误差需求。
ABC方法实现参数间关系建模和分析的过程如下:
第一步,根据实际分析问题的先验概率分布,随机抽取一定数量的可得样本数据,这可能只是先验概率数据总集合的一小部分。
第二步,根据ABC建模方法,从先验概率样本逼近出一个近似后验概率样本,这个计算过程要满足预先设定的逼近精度要求,将误差降到最低。
第三步,根据第二步得到的逼近出的近似后验概率样本,与可以测得的参数观测数据进行比较,如果二者之间的误差足够低,就可以用近似后验概率样本代替表达后验概率分布。
第四步,不断重复前3个步骤,直到获得更低的误差或达到迭代收敛的条件。
将上述方法应用到该文的问题中,假定要分析的铁路桥梁为最常见的简支梁结构,并且结构整体完好无损,即在结构正常的情况下,考察温度和桥梁振动频率之间的ABC模型,如公式(4)所示。
式中:T1为第一次估计时的环境温度;ϕ1()为温度和铁路桥梁第一阶振动频率关系得映射函数;ω1为铁路桥梁第一阶的真实振动频率;为铁路桥梁第一阶振动频率的估计值。
式中:T2为第二次估计时的环境温度;ϕ2()为温度和铁路桥梁第一阶振动频率关系得映射函数;ω2为铁路桥梁第一阶的真实振动频率;为铁路桥梁第一阶振动频率的估计值。
通过上述2个模型建立环境温度和铁路桥梁振动频率之间的估计模型,进而可以进行温度对铁路桥梁振动频率这一刚度性能参数影响的分析。
3 温度对铁路桥梁刚度性能的影响试验
前述工作中完成了铁路桥梁振动频率的采集,构建了环境温度和铁路桥梁振动频率之间关系的ABC估计模型。接下来就环境温度对铁路桥梁振动频率的影响进行试验研究。
先对铁路桥梁所在的试验地的环境温度变化进行统计。2015到2022年间,试验地环境温度每年从1月份到12月份的变化情况见表1。
从表1可以看出,试验地8年来最高温度出现在7、8月份,均值达到了34℃。8年来最低温度出现在1月份,均值达到了5℃。

表1 铁路桥梁实验地2015到2022年间的环境温度变化
接下来,以试验地环境温度和铁路桥梁振动频率的部分样本数据为输入,按照公式(4)和公式(5)建构二者之间的关系模型,迭代过程如图2所示。

图2 温度-铁路桥梁振动频率建模迭代过程
图2中,横坐标为迭代的代数,纵坐标为迭代误差的幅度值F。从图2可以看出,经过9次迭代以后,迭代误差幅度值F基本达到最低,然后稍有起伏到15代以后达到了稳定。其后一直到60次迭代,迭代误差幅度都没再变化。
接下来,根据这个达成稳定的估计模型分析试验地温度对铁路桥梁振动频率的影响,其中对振动频率幅度变化的影响如图3所示。
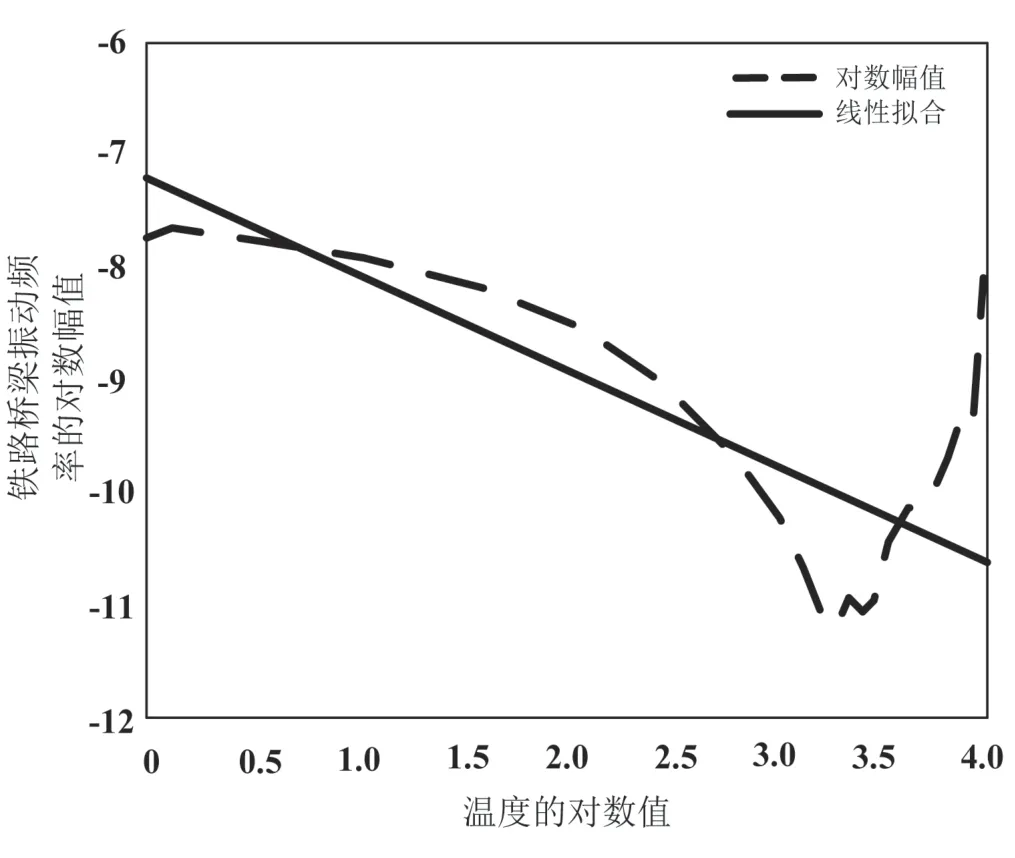
图3 试验地环境温度对铁路桥梁振动频率幅度的影响
图3中,横轴代表了试验地环境温度的变化,纵轴代表了铁路桥梁振动频率幅度的变化,虚线代表了温度-振动频率幅度的关系曲线,实线代表了线性拟合结果。从图3中的结果可以看出,随着环境温度的升高,铁路桥梁的振动频率幅度先下降、后升高,整体趋势是不断下降的。
试验地温度对铁路桥梁振动频率相位变化的影响如图4所示。
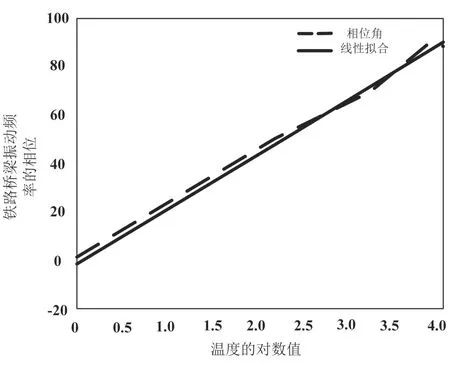
图4 试验地环境温度对铁路桥梁振动频率相位的影响
图4中,横轴代表了试验地环境温度的变化,纵轴代表了铁路桥梁振动频率相位的变化,虚线代表了温度-振动频率幅度的关系曲线,实线代表了线性拟合结果。从图4中的结果可以看出,随着环境温度的升高,铁路桥梁的振动频率相位不断上升。
4 结论
温度对铁路桥梁刚度性能有十分重要的影响,对此进行分析对铁路桥梁的安全稳定运营具有重要意义。该文中,采用希尔伯特变换方法完成对铁路桥梁振动频率的采集,并以此作为铁路桥梁刚度性能的表征参数。其后,以ABC方法代替贝叶斯方法完成温度和振动频率关系的估计。这种方法只需要少量的先验概率样本,并且可以根据先验概率样本逼近出后验概率样本,进而完成估计模型的构建。试验过程中,该文对试验地近8年的温度进行了统计,进一步采用ABC模型就环境温度和铁路桥梁的振动频率关系进行了分析。试验结果表明:在试验地,温度升高对铁路桥梁振动频率幅度有负向影响,对铁路桥梁振动频率相位有正向影响。这一规律对试验地铁路桥梁的运营和维护有指导意义。

