碳纤维增强复合材料加固混凝土粘结性能试验

佘泽昇， 雷冬， 何锦涛， 朱飞鹏， 白鹏翔

(河海大学力学与材料学院， 南京 211100)

碳纤维增强聚合物(carbon fiber reinforced polymer，CFRP)被工程师们广泛应用于土木工程领域，尤其是桥梁工程的加固。大量的工程实例表明使用CFRP材料加固桥梁可以显著提高结构性能和安全性[1-4]。彭晖等[5]考察了混凝土强度、胶层厚度和粘结长度等因素对界面粘结行为的影响，发现胶层厚度、混凝土强度等因素对界面粘结性能存在显著影响。宋文涛等[6]通过对不同配筋率的CFRP编织网混凝土梁的弯曲性能试验，发现试件破坏时编织网纵向受力筋均未达到抗拉强度。刘青青等[7]利用改进的霍普金森杆对不同铺层方式的CFRP板进行低速冲击试验并利用三维数字图像相关方法测量位移场，验证了该方法在研究CFRP板抗冲击性能中的有效应用。邹今航等[8]开展了CFRP加固混凝土梁的静载试验研究，实验表明不同时长的湿热环境处理会使得CFRP加固构件的强化效果减弱。目前的研究大多是使用不同实验方法通过大量的试验数据分析不同因素对CFRP-混凝土界面粘结性能的影响程度，但是在研究不同力臂下的弯剪实验方面还是有所欠缺。

除了不同因素对粘结性能的影响外，许多学者在数值模型方面也进行了深入的研究。童谷生等[9]对5个界面粘结强度模型进行分析评估，并对其中两个进行修正，发现理论预测与试验值有不同程度的精确性。Silva等[10]着重研究了环境老化对本构粘结-滑移曲线的影响。郭樟根等[11]采用修正梁模型对外贴纤维增强复合材料(fiber reinforced polymer，FRP)条带加固混凝土受弯构件的粘结性能进行了试验研究，并计算得到局部粘结剪应力-滑移关系曲线，发现模型与试验结果吻合较好。卢复昌[12]采用ANSYS软件对预应力碳纤维加固混凝土梁进行有限元分析，结果表明初始预应力对界面应力最大值有较大影响。尚亚妮[13]建立了CFRP加固高强混凝土的轴向压缩本构关系并与该类试样的轴心受压试验结果进行对比分析，发现模型计算的结果与实验结果吻合较好。为了研究界面粘结应力的变化走势，在大量的试验数据或有限元的帮助下，可以拟合建立不同影响因素下描述CFRP加固混凝土界面粘结强度和本构关系模型，这些模型的泛用性还需要继续验证。而关于弯剪组合荷载对界面粘结性能影响的理论分析研究也不多，需要深入探讨。

数字图像相关(digital image correlation，DIC)是一种非接触光学变形测量方法，可以得到样品的全场应变分布，适用于CFRP板的变形测量[14-17]。。在之前的工作中，对CFRP外贴混凝土进行单剪试验，并采用DIC法测量CFRP板应变，验证了DIC法测量应变的有效性[18]。因此使用DIC方法进行CFRP加固结构的实验测量是可行的，在许多已完成实验里亦可使用该方法进一步验证。

针对上述问题，现利用专门设计的实验装置进行单剪试验，研究不同力臂的荷载作用下CFRP-混凝土试件界面粘结应力分布关系。采用DIC方法得到CFRP板全场应变并通过对实测应变数据拟合得到应变分布函数。在4种假定前提下推导界面应力应变的理论解，对得到的理论结果进行定性分析并与试验数据对比。通过对弯剪试验应力分布分析，进一步探讨界面粘结应力分布与力臂的关系。

1 试验和方法

1.1 试验装置

为了开展弯剪试验，特别设计了一个装载CFRP-混凝土试件的试验装置(图1)。该装置组成部分有：带4个圆孔的上底板、4根带螺纹的圆形钢条、带7个圆孔的下底板、一块固定混凝土的下挡板、带有3个圆孔的夹具以及上下两根连接试验机的拉头。

其中夹具为产生弯矩而设计，实现力臂变化取决于夹具和下底板对应位置的钻孔，钻孔离CFRP-混凝土粘结界面的距离即为力臂，夹具与下底板各有3个孔，分别对应力臂8.5、16.7、24.2 mm。对每个力臂长度做3组实验，分组如表1所示。

图1 试验装置Fig.1 Experimental device

表1 不同力臂下的试件分组编号

1.2 材料和试样

混凝土试件强度等级为C30(即根据混凝土强度检验评定标准GB/T50107—2010中的立方体抗压强度标准值为30 MPa)，试件尺寸为300 mm×100 mm×50 mm。采用硅酸盐水泥、粗骨料为砾石、细骨料为河砂进行浇注，共浇注9个试件。混凝土配合比如表2所示。

采用的纤维片材为碳纤维板，基体材料为环氧树脂，所用CFRP板的尺寸统一定为300 mm×20 mm×2 mm。混凝土与CFRP板的力学性能如表3所示。

试验使用的黏结胶为环氧树脂A、B类胶，按重量比2∶1混合配置后，将切割并打磨后的混凝土试件的外表面与CFRP 板用搅拌后的环氧树脂胶进行粘结[19]。CFRP-混凝土试件几何尺寸如图2所示。

表2 混凝土配合比

表3 混凝土与CFRP板的力学性能

图2 试件尺寸Fig.2 Geometry size of specimene

数字图像相关法通过光学测量来测量应变。为了获得用于光学测量的散斑场，在完全固化的CFRP板和混凝土表面分别使用白色和黑色的喷漆进行测量。其步骤为：①用白色喷漆将CFRP板材表面喷涂至完全覆盖，并置于通风处等待干燥；②待白喷漆完全干透后，轻喷黑漆使其不连续喷出，在白喷漆上呈点状分布。

1.3 试验方法

将组装好CFRP-混凝土试件的试验装置放在DNS100电子万能试验机上进行试验。采用位移控制模式进行单调加载。在开启试验机前，需调节好试验机的控制程序，设置主要参数——试验机拉伸速率。进行弯剪试验时设置试验机拉伸速率为1 mm/min。数字图像相关(digital image correlation，DIC)摄像机连接计算机，图像采集频率设置为1帧/s。弯剪装置图如图3所示。试验过程如图4所示。

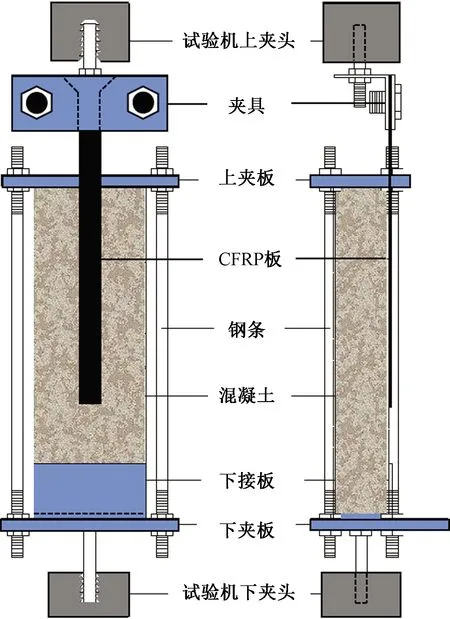
图3 弯剪装置图Fig.3 The bending shear device diagram

图4 现场试验图Fig.4 Field experiment diagram

2 结果与讨论

2.1 理论分析

2.1.1 力学模型

在弯剪情况下其粘结界面受到剪应力和法向应力，DIC所测的CFRP板上的应变分布无法像纯剪试验那样直接由公式得出应力分布，故在分析粘结应力分布时应先进行理论分析，找到控制方程算出应力分布与应变分布，再根据理论分布特征与试验数据进行比较[20-21]。根据本试验设计的界面弯剪试验，其试件受力图如图5所示，弯剪下微元受力分析如图6所示。

由于粘结界面上存在弯曲和剪切两种情况，理论分析应力和最终CFRP板上应变时较为繁琐，故本文假设弯曲和剪切不耦合，在此前提下可分别计算弯曲和剪切产生的应力以及变形，然后叠加即可得到弯剪状态下的结果。剪切和弯曲状态下界面微元受力分析如图7所示。

界面模型计算基于以下4个假设[18]。

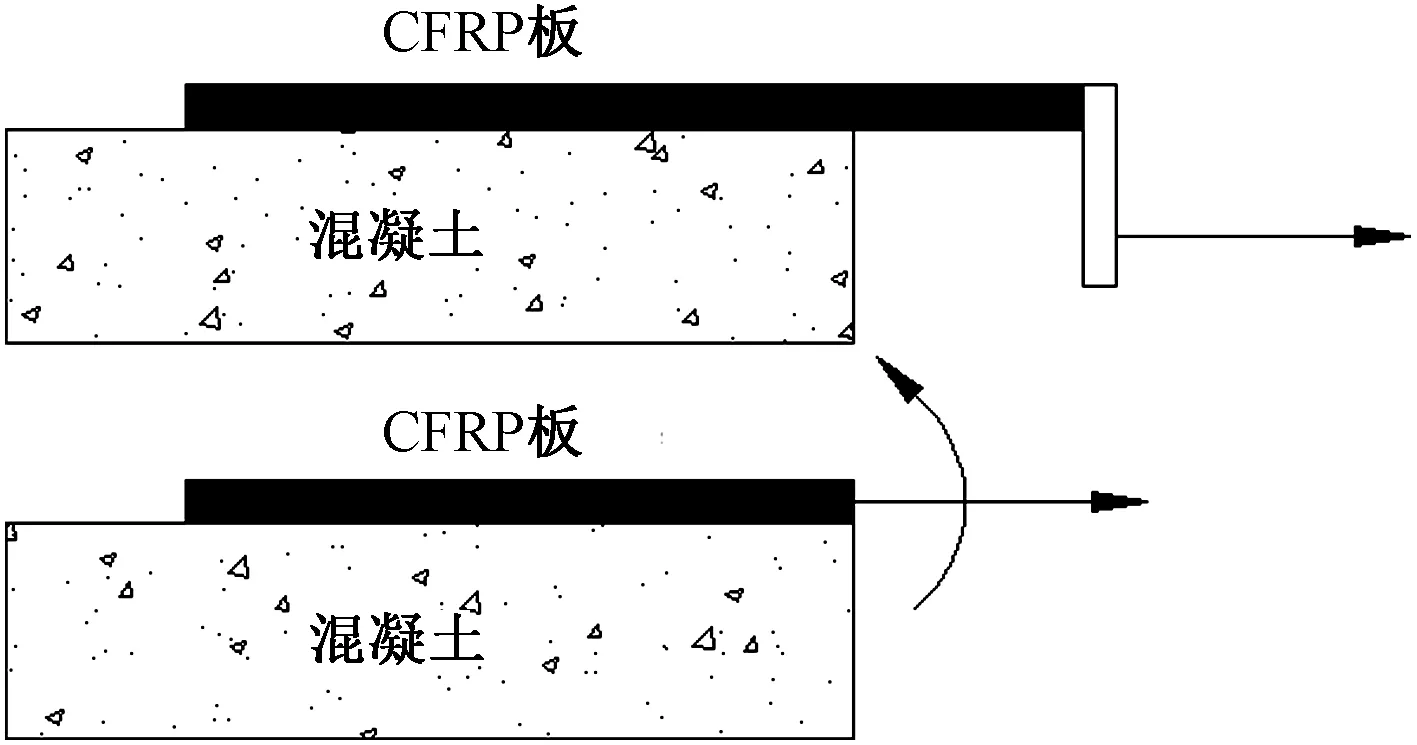
图5 试件受力图Fig.5 Force diagram of specimen

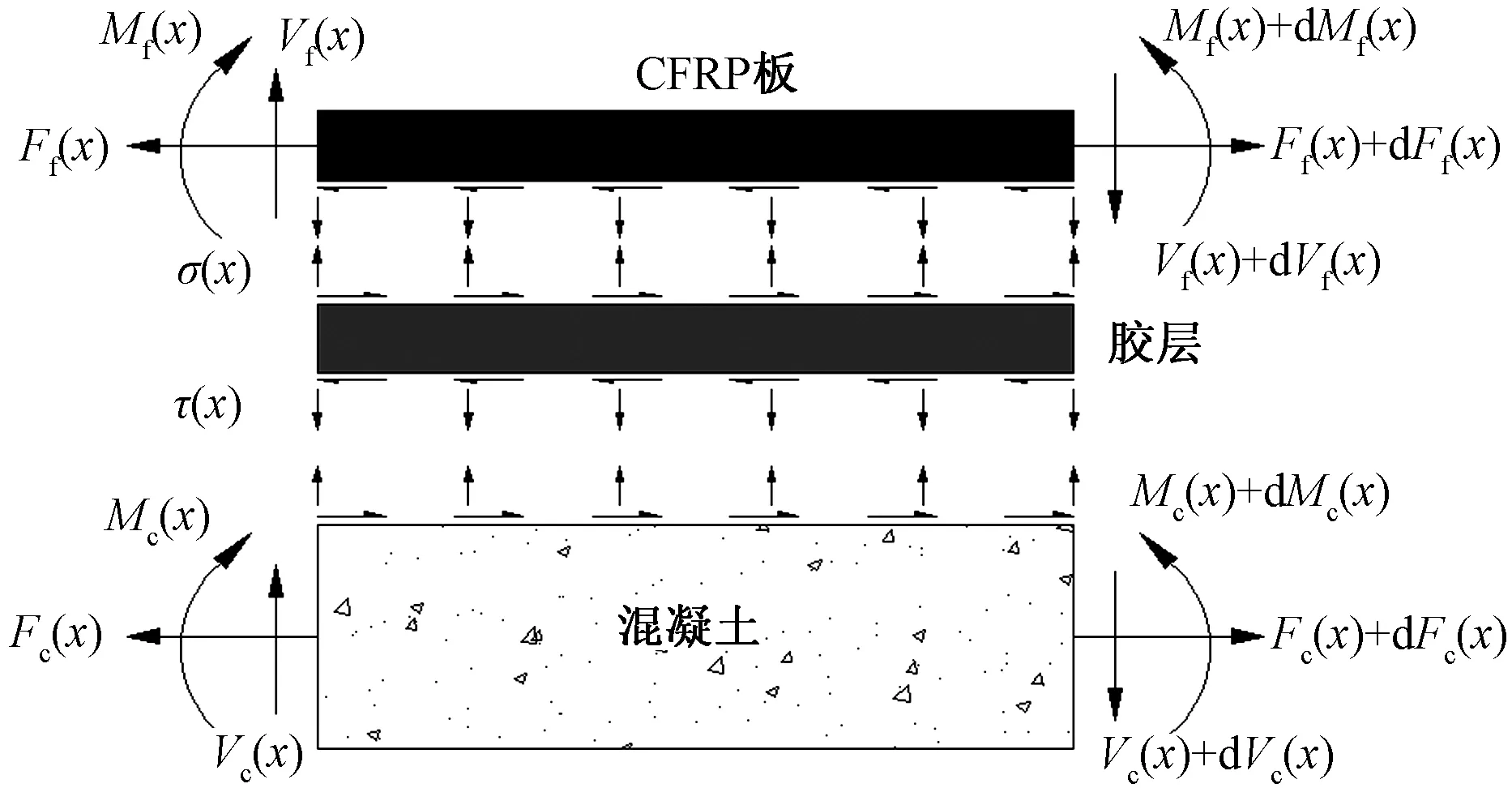
Ff(x)、Fc(x)分别为CFRP板与混凝土所受轴向拉力；Mf(x)、 Mc(x)分别为CFRP板与混凝土所受弯矩；Vf(x)、Vc(x)分别为 CFRP板与混凝土所受剪力；σ(x)、τ(x)分别为粘结界面的 法向应力和剪应力图6 组合状态下微元的受力图Fig.6 Force diagram of the micro-elements in combined state

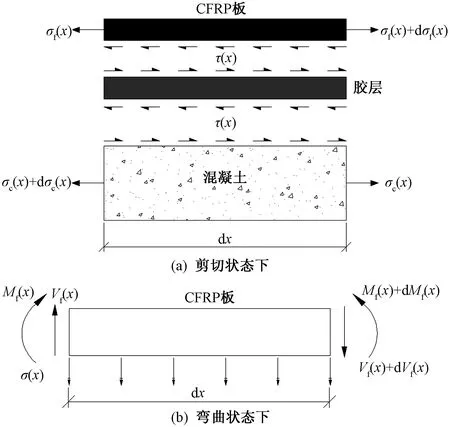
σf(x)和σc(x)分别为CFRP板和混凝土的拉应力,kN/mm2图7 某微段单元的受力分析Fig.7 Force analysis of a micro-segment element

(1)CFRP板始终在弹性范围内即线弹性，沿板长的横截面相同且应力分布均匀。

(2)剪切状态下粘结界面上只有剪应力，CFRP-混凝土试件界面没有最初应力。

(3)沿CFRP板厚度方向应变相同，忽略两种材料在横向上剪切变形对应力的影响。

(4)粘结界面厚度均匀分布且忽略不计，故弯曲刚度忽略不计，只发生横向剪切变形且胶层的水平位移与胶层厚度呈线性分布。

2.1.2 剪切状态理论分析

由图7得CFRP微分单元的平衡方程为

dσf(x)tfbf=τ(x)tfdx

(1)

式(1)中：tf为CFRP板厚度，mm；bf为CFRP板宽度，mm。

对于环氧树脂粘结胶层，其剪应力可由胶层剪应变γxy得

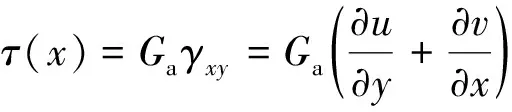
(2)

式(2)中：Ga为胶层剪切模量，MPa；u为胶层某点横向位移，mm；v为胶层某点纵向位移，mm。

根据假设(4)，剪切状态下粘结胶层平面内弯曲刚度可以忽略，故v≈0，由式(1)和式(2)整理再求导可得

(3)

同样根据假设(4)中胶层的水平位移u沿厚度方向为线性分布，则式(3)整理可得

(4)

式(4)中：ta为胶层厚度，mm；uf为CFRP板水平位移，mm；uc为混凝土水平位移，mm；Ef为CFRP板弹性模量,MPa；Ec为混凝土弹性模量,MPa。

对整体微分单元进行平衡分析后整理公式(4)可得微分方程：

(5)

式(5)中：bc为混凝土宽度，mm；tc为混凝土厚度，mm；F为外荷载，kN。

上述微分方程(5)的通解为

(6)

其中常数项系数为

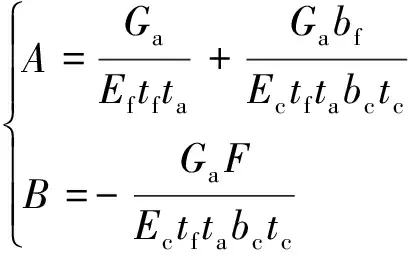
(7)

对还没破坏部分，以CFRP板加载端为坐标原点，沿自由端为x轴正方向，边界条件有

(8)

由边界条件求得方程通解式(6)的系数：

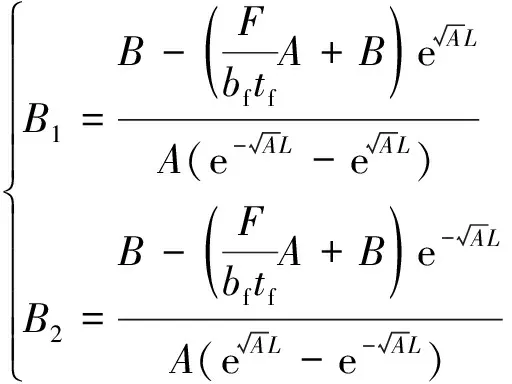
(9)

式中：L为加载端到自由端的粘结长度，mm。

由式(1)和式(6)联立可得

(10)

根据基本假定，CFRP-混凝土界面剪应力可通过以下公式从测量应变得

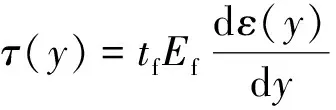
(11)

式(11)中：τ(y)为在任意y处的剪应力，kN/mm2；Ef为CFRP板弹性模量,MPa；tf为CFRP板厚度，mm。

式(7)和式(8)联立可得剪切引起的应变分布：

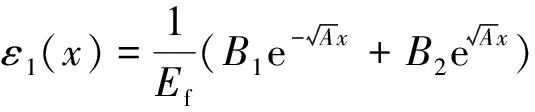
(12)

2.1.3 弯曲状态理论分析

由于混凝土的刚度相比CFRP板的刚度大得多，因此假设混凝土试件相比于CFRP板没有变形。由图7可得CFRP板微分单元的平衡方程为

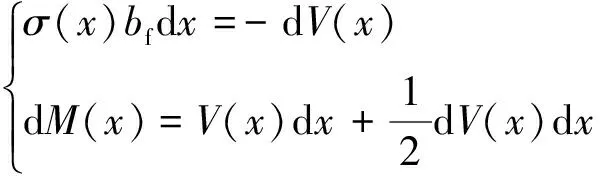
(13)

式(13)中：σ(x)为法向应力，kN/mm2；bf为CFRP板宽度，mm；M(x)为CFRP微分单元所受弯矩，kN·mm；V(x)为CFRP微分单元所受剪力，kN。

为计算法向应力，在此引入胶层的挠度曲线ω(x)可得

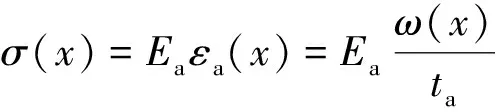
(14)

式(14)中：Ea为胶层弹性模量,MPa；ta为胶层厚度，mm；εa(x)为胶层竖直方向上的应变，kN/mm2。

由于粘结胶层产生的挠度让CFRP板也产生相应挠度，因此可得

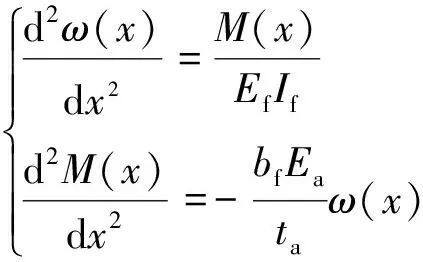
(15)

式(15)中：EfIf为CFRP板抗弯刚度，mm3；bf为CFRP板宽度，mm。

将式(12)整合并对挠度曲线ω(x)求二阶导数得控制方程：

(16)

当x趋于无穷大时，ω(∞)→0，控制方程的通解则为

ω(x)=e-βx[C1cos(βx)+C2sin(βx)]

(17)

对还没破坏部分，以CFRP板加载端为坐标原点，沿自由端为x轴正方向，边界条件有

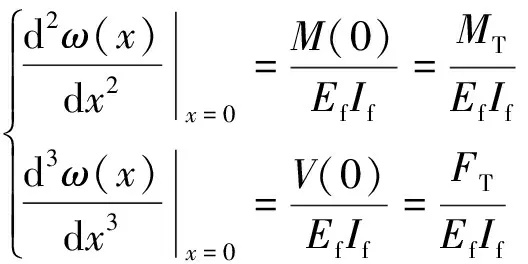
(18)

式中：MT为加载端的弯矩，kN·mm；FT为加载端的剪力，kN。

将通解式(17)代入边界条件可得

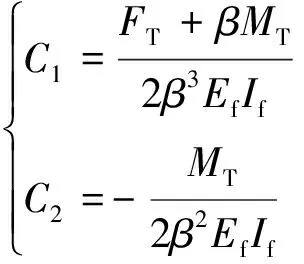
(19)

将式(14)代入挠度通解式(17)可得法向应力：

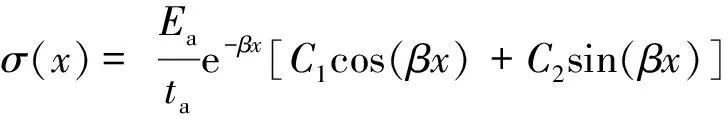
(20)

法向应力引起的正应变ε2则由式(21)与通解[式(17)]联立得到。

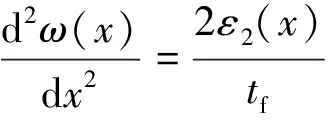
(21)

ε2(x)=tfβ2e-βx[C1sin(βx)-C2cos(βx)]

(22)

将剪切和弯曲状态下得到的应变分布叠加即式(9)和式(17)相加得到总应变分布：

tfβ2e-βx[C1sin(βx)-C2cos(βx)]

(23)

2.2 实验结果

2.2.1 CFRP板应变分布特征

Pu为极限荷载图8 试件BS8.5-2上CFRP板应变分布Fig.8 Strain distribution of CFRP plate on specimen BS8.5-2

将DIC测量的照片导入vic-2D计算机分析软件，计算不同加载阶段CFRP板表面的应变分布图。以试样BS8.5-2为例(图8)，根据实测和计算结果，得到CFRP板的垂向应变分布特征和演化过程。加载初期加载端负应变最大，随着荷载的增加，板的大部分区域的负应变值增大，负应变峰值位置朝自由端移动。当负应变峰值到达板中央时，可以看到加载端的应变值已变成正值，说明该部分已经脱粘。加载末期，负应变峰值位置接近自由端，而加载端的正应变值已经发展到四分之一板处，说明裂缝已经扩展不少。

2.2.2 应变分布曲线演化

图9为不同力臂下实际应变分布曲线，展示加载中期以后几个时段的应变曲线，由曲线分布特征可以推测每个荷载下CFRP板与混凝土开裂长度。例如试件BS8.5-2中80%极限荷载下开裂的长度大致上是50 mm，其脱粘区域的CFRP板段承受拉伸和弯曲作用，在原加载端位置拉伸作用大于弯曲作用，应变值为正，沿板长方向应变值降为负值，可知此时弯曲效应已大于拉伸效应，在粘结区域达到负应变峰值。

从图9可以得到：脱粘区域中随力臂的增加，CFRP板受拉伸影响小于弯曲，整个CFRP板的应变为负值；当同试件中荷载越大时，加载端的负应变变小，说明拉伸作用的影响变大。

由于弯剪状态下的应变推导解析过程仅适用于弹性状态，开裂涉及开裂本构关系，比较复杂，因此本文没有针对脱粘区域进行解析。在推导时由于开裂都是由加载端开始的，CFRP板本身在脱粘区域也有应变，因此实际粘结区域应变数据与理论推导数据不符，故将以理论应变分布进行定性分析，与实际应变对比分布特征情况。对比BS8.5-2的80%极限荷载下的剪切和弯曲引起的应变分布和总应变分布以及不同力臂在极限荷载作用下的总应变分布曲线，如图10所示。

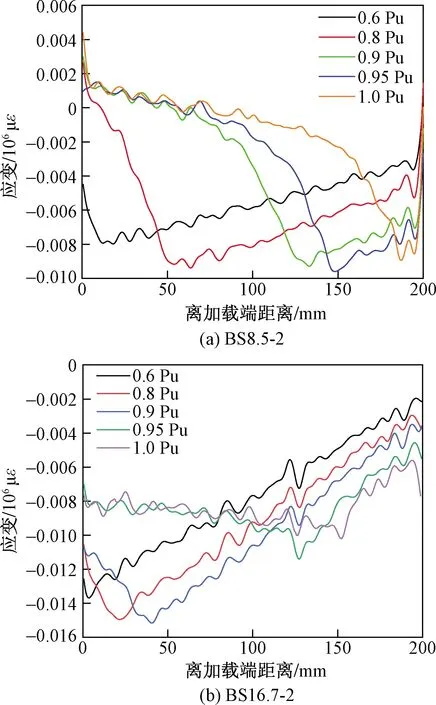
图9 不同极限荷载下应变分布曲线Fig.9 Strain distribution curves along the CFRP plates

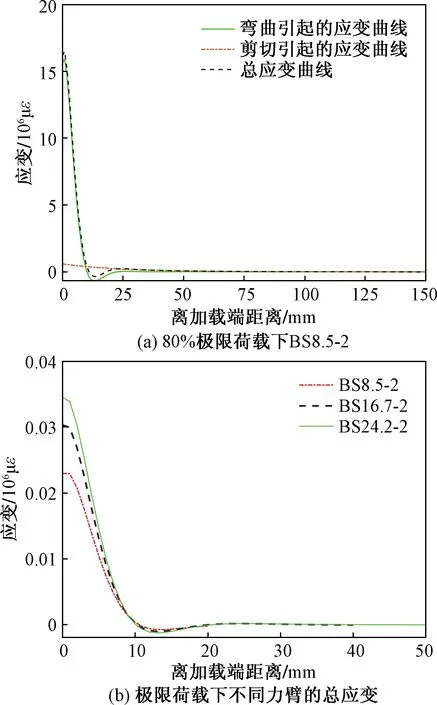
Pu为极限荷载图10 应变分布曲线Fig.10 The strain distribution curve

由图10(a)可知：①剪切引起的应变分布特征沿板长逐渐减小到零，弯曲引起的应变分布则是加载端应变值最大，骤降到离加载端12 mm左右为负应变峰值，而后上升至很小的正应变，最后缓缓下降到零；②剪切引起的应变相比于弯曲引起的应变量级差太多，导致其应变没有在总应变中表现出来，故总应变分布曲线与弯曲引起的应变曲线相似，且负应变区域依旧不变。从图10(b)可以看出：随着力臂的增大，剩余粘接区加载端应变峰值也随之增大。负应变区位置与上述相同，且不随弯矩的改变而改变，总体分布趋势相同。

在理论推导中，开裂后粘结区应变分布的边界条件与开裂前相同。这种情况会导致开裂后与开裂前的应变分布曲线特征相同。因此从粘结区域实际应变分布曲线的特征可以看出，应变分布特征与理论推导分析一致，说明试验是有效的。

图11 不同荷载下试件BS8.5-2的界面应力分布曲线Fig.11 The stress distribution curve of specimen BS8.5-2 under different loads

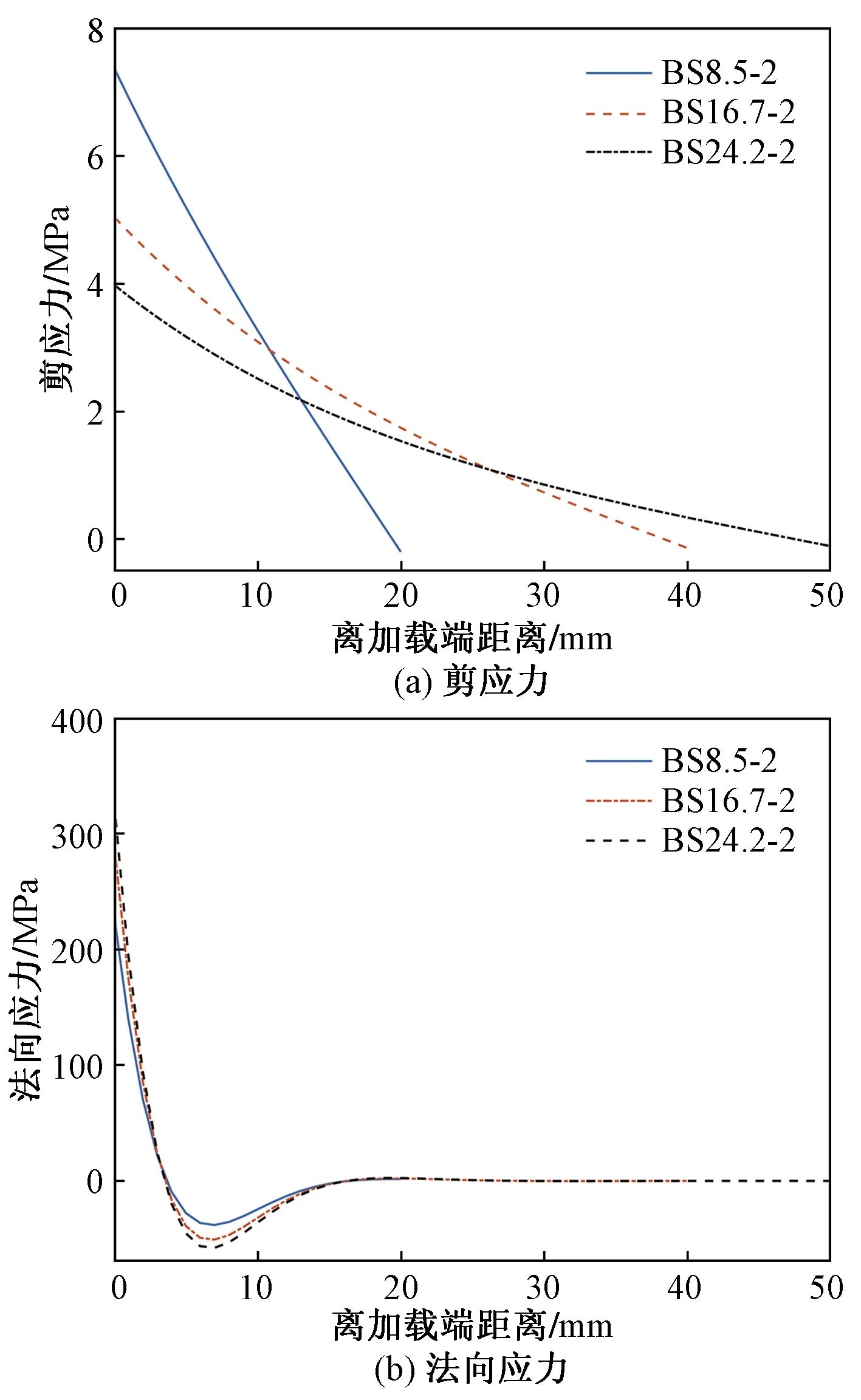
图12 不同力臂下试件的界面应力分布曲线Fig.12 The stress distribution curve of specimen under different moment arms

2.2.3 应力分布曲线演化

在解析粘结区域的粘结应力时发现不论荷载多大，其粘结区域的应力分布特征几乎没变，以试件BS8.5-2为例，选取60%、80%、90%和100%极限荷载下的剪应力与法向应力分布曲线，如图11所示。在极限荷载作用下不同力臂的界面粘结应力分布曲线如图12所示。

从图11的应力分布曲线可以看出：①同一试件中，剪应力峰值(在加载端)随荷载的增加而增加，剪应力在粘结区域内的分布特征相同，由加载端递减至零；②法向应力峰值与剪应力相同，荷载增加，其分布特征变化不大，由加载端的正应力峰值骤降至离加载端6 mm左右的负应变峰值，而后上升到一段极小的正应力后到离加载端28 mm左右下降至零。故在弯剪试验中，弯曲作用产生法向应力在CFRP板上有一有效区域，超过有效区域的板段不作用法向应力。

由图12可知：①剪应力在加载端的应力峰值随着力臂的增加而减小，而法向应力在加载端的应力峰值随着力臂的增加而增大，说明随着力臂的增加，CFRP板受弯曲的影响也在增加，相对而言受拉伸的影响变小；②剪应力与法向应力分布与不同荷载情况下一样，受弯曲作用而产生法向应力的有效区域仍然是从加载端到离加载端28 mm左右。其中正应力的区域为0～3 mm和16～28 mm，负应力的区域为3～16 mm。

3 结论

(1)CFRP-混凝土界面粘结剪应力分布不均匀，受粘结胶的传递系数影响；弯剪破坏中由于弯矩的存在，使得CFRP板与混凝土之间的粘结强度大大降低，导致极限荷载的减小，且力臂越大，极限荷载越小。这对CFRP-混凝土界面粘结性能是不利的，将会减少使用寿命。

(2)对比弯剪试验中理论和实际应变分布曲线，发现两者的应变分布特征具有一致性。弯剪试验中分析CFRP板表面应变-板长分布，可大致估计CFRP板的剥离长度，在工程应用中对已剥离长度的确定可以减小维护工作量。

(3)弯剪试验中产生法向应力的区域从加载端到离加载端28 mm左右，且这个区域不随荷载以及力臂的改变而改变，表明粘结区域受弯曲作用产生法向应力有一个固定的有效区域，超过这个区域便不产生法向应力。因此在工程应用中受弯拉组合作用的CFRP板加固混凝土可以在加载端的应力有效区域内进行再次加固，增加使用寿命。

(4)弯剪破坏中界面粘结应力包括剪应力与法向应力，两者的应力峰值都在加载端且都随着荷载的增加而增大，而在另一方面剪应力峰值随着力臂的增加而减小，法向应力峰值则随着力臂的增加而增大。随着开裂长度不断增加，实际粘结界面的剪应力与法向应力以接近平移方式移动，使得实际粘结区域上的应力分布曲线特征不变，仅数值上发生改变。