花岗岩动态劈裂拉伸实验及动力作用机制

郭占峰， 满轲

(1.河南省城乡建筑设计院有限公司， 郑州 450002； 2.北方工业大学土木工程学院， 北京 100144)

岩石属于一种准脆性材料，其静态力学或者动态力学性质均在岩土工程中获得了大量的应用，如在隧道开挖、露天矿山作业、巷道掘进、海底空间支护、爆破施工等工程中。科学合理的借助岩石力学参数用于工程分析，具有显著的工程指导意义，甚至可为工程进度、工程预算、工程技术重难点等方面提供重要的制定与设计依据。通常在工程现场，岩石介质所受到的载荷包含多种，可分为静态荷载和动态荷载两类，静态荷载如地应力、静水压力等，动荷载如爆破荷载、机械掘进导致的扰动荷载、动水压力等，其包括了从低应变率到高应变率范围的各种类型的动态载荷，并且指出实际工程中予以大量应用的是动态荷载，静态荷载在某种角度上(加载更为缓慢)亦属于一种动态荷载[1-3]。因此，无论是静态荷载还是动态荷载，在岩土工程中都有着极为强烈的应用属性，是岩土工程设计、施工、支护、运维等多个阶段的重要考量。

众所周知，岩石作为一种准脆性材料，其抗拉强度远远小于其抗压强度，也就是说，岩石更容易被拉坏，甚至在压缩受力过程中，破坏形式也往往是由其内部的微裂隙发生拉伸破坏而导致的整体破坏。不同的强度破坏准则蕴含着物质材料的破坏机理，而拉伸破坏对于准脆性材料而言更为普适[4-6]。鉴于岩石的抗张拉强度远小于其抗压强度，导致岩石更易发生拉伸破坏，所以决定岩石破坏的主要力学因素之一为岩石的抗拉伸力学性能。同时，岩土工程中，动荷载更易导致岩石介质发生破坏，岩石的静力行为多与其动力行为相互交织，互为耦合，共同作用[7-9]。因此，岩石在动荷载作用条件下的抗拉伸力学特性研究就变得尤为重要。

在动载荷作用下，岩石的力学响应与静态条件下相比存在显著差异，有很明显的应变率效应[10-12]。近年来，在岩石的动态力学性能方面尤其是岩石动态抗拉力学特性方面，引起众多学者研究[13-16]。其中，应力波传播规律及其衍生而来的效应对于研究岩石材料动态力学性能是不可忽略的，同时也是动力学行为研究的一个重要方面[9,17]。在破岩或者爆破开挖工程中，岩石承受的均为动态载荷作用，其应变率范围一般为101～103s-1[18]。目前，岩石动态力学性能研究主要是利用分离式霍普金森压杆(split Hopkinson pressure bar，SHPB)实验装置，结合不同尺寸的岩石试样予以不同力学性能试验，进而获得其力学特性，从而指导工程实际。对于岩石静态拉伸试验而言，由于岩石材料的直接拉伸实验操作难度大，通常采用间接实验方法测量拉伸性能，最常用的就是巴西圆盘实验，即劈裂拉伸实验[19]。同理，对于岩石动态拉伸试验，亦采用间接拉伸(巴西劈裂)的方法进行测量。因此，采用SHPB实验装置进行岩石动态劈裂拉伸实验，已成为研究岩石动态拉伸性能中一种高效且简便的实验方法。胡时胜[20]对Hopkinson压杆实验技术的应用进展进行了相关整理总结，认为SHPB装置不仅适用于准脆性介质，同时还可推广应用至软弱材料及波阻抗小的泡沫介质材料等；并且侧重对入射波形的整形技术予以了分析。宋小林等[21]应用SHPB对具有不同尺寸的大理岩试样，分别采用巴西圆盘和带平台的巴西圆盘试样进行了宽应变率范围的动态劈裂拉伸实验，总结出不同形状大理岩试样在动态劈裂过程中的破坏应变以及强度变化规律。宫凤强等[22]通过对巴西圆盘试样进行SHPB冲击实验研究，提出巴西圆盘劈裂实验中拉伸模量的解析算法。进一步的，分别采用INSTRON公司的液压伺服试验机和SHPB冲击装置，提出了一种基于率效应的动态增强因子统一模型，该模型可较好地描述不同加载率条件下的动态压缩强度和切线模量。文献[23-26]系统总结了岩石动力学的最新研究成果，着重介绍了岩石动态拉伸在围压共同作用下的测试装置、测试原理、试验方法及试验结果等，进一步讨论了深部岩石动态拉伸力学强度的变化规律及互馈作用机制。综上，目前对岩石动态压缩以及围压作用下的动态力学性能研究较多，但是有关岩石动态拉伸力学性能的研究还较少。

基于此，现采用在岩石巷道开挖掘进工程中普遍存在的花岗岩类岩石试样。基于SHPB实验装置以及巴西劈裂拉伸原理，对花岗岩试样开展不同冲击速度下的动态劈裂拉伸实验，分析花岗岩试样的动态拉伸力学性能，以期为岩巷高效掘进、巷道支护方案设计，以及精细化施工等工程实际需求提供切实的指导参数、设计依据、监测方案与最终的解决方法。

1 动态拉伸劈裂实验

采用的SHPB实验装置，其直径为50 mm。采用不同的冲击加载速率，对花岗岩试样进行动态劈裂拉伸实验，分析其破坏形态，进而对冲击荷载作用下花岗岩试样的动态拉伸力学性能予以系统分析与深入研究。

1.1 实验装置

图1 SHPB实验装置系统Fig.1 The system of SHPB experimental device

SHPB实验装置是进行岩石动态拉伸试验的主要设备。该杆径为50 mm的SHPB实验装置系统，如图1所示，SHPB装置系统主要由撞击杆、入射杆、透射杆和阻尼装置构成，附以必要的数据采集装置(超动态应变仪等)。其中，粘贴在入射杆与透射杆上的应变片提供了冲击试验全过程的数据。实验时花岗岩试样应沿杆轴径向放置在入射杆和透射杆之间。在入射杆杆端放置有波形整形器，可对入射波形予以调整，获得上升波沿信号稳定的入射波。其中，撞击杆以速度v发射，与入射杆撞击接触。

1.2 实验原理

在本次动态拉伸实验中，入射杆中产生的入射应力波在花岗岩试样内部经过若干次反射与透射，继而导致试样破裂，应力波作用的冲击过程模拟如图2所示。

t为试验时间；εi为入射杆上入射波的应变值； εr为入射杆上反射波的应变值；εt为透射杆上透射波的应变值图2 动态巴西圆盘劈裂实验Fig.2 Dynamic Brazilian disc splitting test

根据一维应力波以及内部应力近似均匀分布假定[27-28]，通过对实验数据的动态力平衡验证，实验数据有效可靠，即εi+εr=εt，可采用两波法对实验数据进行处理，认为试样端面受力近似相等。根据SHPB实验技术的两个基本假定与巴西圆盘劈裂原理，花岗岩试样的动态拉伸应变、应变率及杆端应力计算公式为

(1)

(2)

σ=EAεt

(3)

Rodriguez等[29]基于光弹实验，并通过有限元模拟计算，获得了静态巴西圆盘劈裂过程中的受力特性。进一步的，其运用ANSYS软件，计算模拟了动态巴西圆盘实验中试样的受力与变形，认为无论是静态还是动态巴西劈裂试验，当岩石试样内部应力达到平衡后，其动态应力分布情况与其静态应力分布情况保持一致，只是在岩石试样的加载端面处存在有微小的差别。因此，根据巴西圆盘静态劈裂试验获得的拉伸应力计算公式，与式(3)相结合，可以获得岩石试样的动态拉伸应力：

(4)

式(4)中：D和B分别为试样的直径和厚度。

需特别说明的是，同静态巴西圆盘劈裂试验测试结果一样，式(4)所测得的动态拉伸应力值为岩石试样中心点处的应力。

1.3 花岗岩试样制备

对于花岗岩测试试样，按照国际岩石力学学会制定颁布的动力学实验规程的要求加工试样并开展相应的试验。在实验室内，分别采用2S-200型立式取芯机、DQ-4型岩石切割机、SHM-200型双端面磨石机对岩样进行钻取、切割、打磨等作业，使加工后岩石试样的不平整度和不垂直度均小于0.02 mm，并且需保证试样的高度、直径误差均小于0.3 mm。

该批次试验所需岩石试样的加工规格为Ф25 mm×50 mm，为圆柱形试样，加工后的试样如图3所示。

图3 制备的花岗岩试样Fig.3 Processed fine granite samples

1.4 实验过程及结果

基于SHPB实验装置，对花岗岩试样实施动态劈裂拉伸实验时，需要密切关注在冲击试验启动之前，入射杆和透射杆是否将测试试样牢固夹紧，同时，还需确认测试试样的径向与冲击压杆的轴线是否处于共轴状态。

为了尽量减小测试试样与实验装置之间的摩擦力作用因素，降低加载端面约束对试样内应力分布状态的影响，需在冲击测试前将凡士林涂抹在试样与入射杆的端面接触处；同时，需在入射杆端部装置波形整形器。

继而，根据国际岩石力学与工程学会的试验规程，开展不同加载速率条件下的花岗岩试样冲击试验，在此不再一一赘述。本次实验共对75块花岗岩巴西圆盘试样进行了冲击实验，其中取得有效试验数据的试样个数为70个。按冲击速度每0.5 m/s的步长，将步长范围内所有试样的速度、应变率、应力峰值、弹性模量等分别求其平均值，共获取了19组数据，花岗岩试样劈裂拉伸实验统计如表1所示，变形性能参数如表2所示。

表1 花岗岩试样劈裂拉伸实验统计表Table 1 The impact test results of granite specimens

表2 变形性能参数Table 2 Deformation performance parameters

2 花岗岩试样破坏形态与力学特性分析

2.1 破坏形态

不同的冲击速度对应于不同的加载速率，其测试试样的破坏形态亦不相同，存在着显著的差异。花岗岩试样破坏后的表面形貌重构以及其破坏形态研究，对于深入分析测试试样的变形特点及破坏规律具有重要的参考价值。

不同冲击速率下SHPB劈裂拉伸实验后，对冲击破坏后的花岗岩试样分别搜集、整理、拍照，分析其不同加载速率下的破坏形态，其典型的破坏形态如图4所示。

可见，花岗岩试样在不同速度冲击下呈现出不同的破坏形式。大致可分为完整、存在细小裂缝、整体破裂、完全粉碎等4个破坏形态。其中在冲击速度小于6 m/s时(应变率约在100 s-1内)，试样未破坏，内部刚萌生裂纹，试样仍保持完整，吸收的冲击能量只是在试样内部造成损伤；冲击速度为6～8 m/s时，试样吸收的冲击能量导致其内部及表面均出现了众多的细小裂缝及若干宏观裂缝；冲击速度处于9～10 m/s时(应变率在100～150 s-1)，试样呈现出破碎形态，被冲击能量破坏；冲击速度大于11 m/s时(应变率超过150 s-1)，试样完全粉碎，冲击能量远远超过了试样自身所能吸收的能量，较多地转化为破坏试块的动能。上述现象说明了：随着冲击加载速率的提高，入射动能增加，岩石内部破裂面越来越多，破碎块度随之增加。

图4 不同冲击速度下破坏形态Fig.4 Failure mode of different impact velocity

2.2 力学特性分析

根据式(1)～式(4)，对于不同冲击速度下采集到的花岗岩试样，将其反射波信号及透射波信号应用二波法进行数据拟合与处理，得到不同冲击速度下花岗岩试样的应力-应变曲线，如图5所示。需要说明的是，此处的应变为试样的径向应变。

从图5可以看出，随着应变率的增大，应力-应变曲线幅值也随之增大，并且上升沿斜率随加载速率的增加而显著增大；也就是说越大的应变率，试样的应力变化幅值越为明显，具有强烈的应变率效应属性。

图6为试样峰值应力与应变率关系图，由图6可知，花岗岩试样的峰值应力随应变率的增加而逐渐增大，峰值应力与应变率呈现出较好的线性关系，亦表明准脆性介质的应变率效应，两个参量之间具有定量化关系，其具体表达式为

(5)

图7为花岗岩试样的峰值应变与应变率关系，由图7可知，花岗岩的峰值应变随应变率的逐渐增加，其峰值应变逐渐减少。

图5 动态劈裂拉伸应力-径向应变曲线Fig.5 Dynamic splitting tensile stress-radial strain curve

图6 峰值应力-应变率曲线Fig.6 Peak stress-strain rate curve

图7 峰值应变随应变率变化Fig.7 Peak strain varies with strain rate

同峰值应力与应变率关系类似，其峰值应变与应变率亦呈现出较好的线性关系，两个参量之间的拟合关系式为

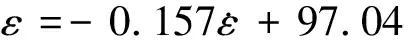
(6)

式(6)中：ε为峰值应变。

进一步的，综合图6与图7可知，花岗岩试样的峰值应力与应变率呈正比，但是其峰值应变与应变率成反比，即随着应变率的提高，花岗岩的峰值强度不断增强，但是峰值应变却逐渐减小，这充分说明了随着应变率的提高，花岗岩这一准脆性介质的变形能力在逐渐变差，更易被破坏。

2.3 拉伸敏感性及率效应分析

为了定量地衡定岩石拉伸强度的率效应特征，界定了拉伸敏感性这一指标[30-31]。该指标定义为岩石的动态拉伸强度与其静态拉伸强度之比，也就是说，岩石拉伸敏感系数这一参数表征的物理含义是：岩石的抗拉强度对应变率变化的敏感性。

拉伸敏感系数用DIFC计算公式为

(7)

式(7)中：fcd为动态单轴冲击拉伸强度；f′c为准静态单轴拉伸强度。

静态拉伸力学测试如前所述，采用的是巴西劈裂试验，以压代拉，为常见的岩石力学特性测试试验，在此不再赘述。其中，花岗岩试样的静态单轴拉伸强度经静态力学测试，获得的结果平均值为12.59 MPa。

图8为试样的拉伸敏感系数随应变率的变化，从图8可知，在花岗岩试样的动态劈裂实验中，随着应变率的提高，其拉伸敏感系数亦在逐渐增加，其变化趋势总体上呈现为正比关系。

图8 拉伸敏感系数随应变率变化Fig.8 Tensile sensitive coefficient varies with strain rate

二者虽不是近似的线性变化规律，但是图8仍表明了拉伸敏感系数与应变率之间存在着强相关性，这一方面说明了该指标(拉伸敏感系数)的定义有明确的物理意义，能够合理地表征动态拉伸强度的力学属性，另一方面也充分说明了花岗岩为应变率敏感性材料。

图9为试样的弹性模量与应变率的关系，由图9可知，测试试样的动态弹性模量随应变率的增加而逐渐增大，并且，弹性模型的变化幅值随应变率的增加而逐渐增大，曲线斜率逐渐增陡，进一步表明了弹性模型为应变率敏感性参量。该参量是由应力与应变共同决定的，二者的相互耦合加速了该参量的变化。

图10为冲击速度与应变率的关系曲线，由图10可知，随着冲击速度的不断增加，其应变率逐渐增大，该冲击速度与应变率呈较好的线性关系，同样说明了花岗岩为一种应变率敏感性材料。其应变率与速度之间存在如下关系：

(8)

式(8)中：v为撞击速度。

图9 弹性模量随应变率变化Fig.9 Elasticity modulus varies with strain rate

图10 速度-应变率关系Fig.10 Velocity-strain rate relation diagram

3 动态冲击拉伸过程数值分析

3.1 动态劈裂模型建立

图11 动态劈裂有限元模型Fig.11 The dynamic split finite element model

采用有限元软件ABAQUS，对该冲击劈裂试验过程进行了数值模拟与分析，其有限元模型及网格划分如图11所示。其中，将试样沿径向划分60个，轴向划分60个，冲头、入射杆、试样、透射杆的几何模型的单元数为3 600、15 000、15 000、12 000。所建模型为对称结构，为了简化计算，建立1/4的计算模型即可。在x和y轴垂直的界面上分别施加x和y方向的位移约束，位移设置为0。

3.2 破坏过程数值模拟分析

借助动态冲击劈裂的数值模拟，可对该冲击劈裂试验予以全过程分析，可分辨出其大致分为以下三个作用阶段。

(1)子弹冲击，当接触入射杆后，在入射杆中产生一维的入射脉冲应力波，并沿着入射杆件快速向前传播。

(2)入射波进入试样后，在试样中来回折反射，数次之后，达到应力平衡，试样两端的应力基本上维持平衡与稳定状态。

(3)一部分应力波在入射杆中发生反射，并与后续进入入射杆的入射波产生叠加；一部分应力波经过试样后，进入透射杆中，产生透射波。

整个应力传播模拟过程如图12所示。

图12 模拟劈裂过程的三个阶段Fig.12 The three stages of the splitting process

通过图12可知，在冲击应力波的短时间作用下，试样两个接触端面很快就发生局部的应力集中，随着冲击时间的增加，该应力集中现象进一步加剧；与此同时，试样在入射应力波作用下，其内部受集中应力波力的作用，产生了破坏开裂，内部裂纹从试样的中间位置处开始向两端部衍生，沿着杆件与试样的接触面快速传播，直至该裂纹贯通试样，导致试样完全开裂破坏。同时，当裂纹产生后，裂纹两端的应力瞬间快速向周边传播弥散。

将实验结果与数值模拟结果进行比较，可知试样在不同冲击速度下，其冲击裂纹基本均为直线型，并且裂纹产生及其范围均是从花岗岩试样的直径处开始，沿着径向，向两接触端部衍生。

4 讨论

Reinhart等[32]认为，在较高的加载速率下，裂纹速度的降低往往能够增加岩石的强度。稳定裂纹扩展过程中的裂纹扩展速度通常用Griffith理论估计，即0.38c(c为应力波的传播速度)。在本文研究中，c约为4 000 m/s；因此，裂纹扩展速度约为1 500 m/s。计算I型和IV型所述试样中断裂面的形成速度，以确定断裂面的裂纹扩展速度。Ⅰ型的形成速度为640 m/s，Ⅳ型的形成速度为1 600 m/s，Ⅳ型的速度接近预测速度，但Ⅰ型的速度要慢得多。因此，在较高的应变速率下，裂纹扩展速度降低，导致较高的动态拉伸强度。这与Reinhart等[32]的研究结果一致，并且表明在本文研究中获得的动态拉伸强度包括有与裂纹扩展速度相关的作用机制。

综上，基于Hopkinson效应和劈裂现象相结合的动态抗拉强度受岩石的不均匀性、应力速率、相邻微裂纹处释放的应力引起的裂纹止裂以及裂纹扩展速度等因素的共同影响。

5 结论

借助SHPB装置，进行了不同加载速率条件下，一系列花岗岩试样的动态劈裂拉伸实验，对其动态力学参数与应变率进行了关联分析，并提出了拉伸敏感性指标，探讨了拉伸敏感性的率效应，结合数值模拟结果，讨论了岩石动态拉伸试验的本质，得出以下结论。

(1)在动态劈裂实验中，通过对花岗岩峰值应力与应变关系的分析，得出花岗岩试样的峰值应力表现出强烈的应变率效应，在不同加载速率下破坏形态各异；提出的动态拉伸敏感性指标物理意义明确，能够准确反映岩石类准脆性介质在动态拉伸受力情况下的率效应。

(2)用ABAQUS软件模拟了SHPB动态劈裂过程，在冲击劈裂初始作用时，试样与入射杆和透射杆接触面的损伤范围较大，随着冲击劈裂试验的进行，与试样实际破坏形态相吻合，裂纹从试样的中间位置开始向两端部衍生传播。

(3)本质而言，岩石的动态抗拉强度受到岩石的不均匀性、应力速率、相邻微裂纹处释放的应力引起的裂纹止裂以及裂纹扩展速度等因素的共同影响与相互作用。