基于双循环改进landweber电容层析成像图像重建
严春满刘晓敏
(西北师范大学物理与电子工程学院,甘肃 兰州 730070)
电容层析成像技术(Electrical Capacitance Tomography,ECT)是一种基于电容敏感场的过程层析成像技术,系统主要由电容传感器单元、数据采集单元、计算机图像重建单元三部分构成,由于其结构简单、成本低、无辐射等优点,被广泛应用于多相流检测等工业领域中[1-2]。
ECT成像系统通过电容传感器获取不同电极对间所有电容值,经数据采集单元收集全部信息并传送至计算机得到各介质分布图像[3],故ECT图像重建的核心是计算机图像重建单元,其根据相应的图像重建算法反演出不同介质分布图像,从而实现多相流的可视化测量[4-5]。而工业应用的关键是能快速有效的得到高精度的介质分布图像,故成像算法的改进和优化成为ECT图像重建技术研究领域的主要关注方向之一。
目前,ECT图像重建算法大致分为直接算法、迭代算法及智能算法,其中直接算法包括线性反投影(LBP)算法[5]、Tikhonov正则化[6]等。LBP算法结构简单、计算速度快,各流型成像质量较差,一般只用于定性分析;Tikhonov正则化是解决非线性不适定问题的有效方法,但其参数选取不易,易影响重建精度。相对而言迭代算法成像效果更优,如NewtonRaphson算法[7]、Landweber算法[8]。NewtonRaphson算法又被称为迭代Tikhonov正则化,即借鉴Tikhonov思想为传统NewtonRaphson算法添加一个单位矩阵,其重建图像主观效果与正则化相当;Landweber算法是典型的迭代算法,其算法复杂度适中,常用于ECT成像。智能算法目前主要以神经网络[9]为主,其成像效果较佳,但所需样本获取不易且训练时间较长。
Landweber算法是解决ECT非线性不适定问题最常用的迭代算法,但其迭代次数较多、稳定性较差且重建图像精度较低,为改善其不足提出了许多改进算法。文献[10]基于12电极传感器系统将Runge-Kutta算法应用于landweber,证明了其收敛性并探讨了应用于ECT的可行性;文献[11]基于同伦摄动方法改进landweber,推导出二阶迭代公式并通过添加约束因子改善其半收敛性,提高重建图像质量。文献[12]针对ECT病态问题,提出一种基于修正隐式Landweber成像算法,该算法易实现且稳定性好。文献[13]通过构造压缩算子改进Landweber算法,达到全收敛并提高了重建精度。本文针对Landweber算法的不足之处,分析其原理并通过构造残差矩阵添加权重因子使其达到稳定收敛条件,再根据Frozen Landweber迭代格式[14],将其进行内外双重循环,获得本文改进算法并将其应用于ECT图像重建,提高了稳定收敛速度和重建图像精度。数值仿真实验结果表明改进算法的客观评价指标和主观图像重建质量优于 NewtonRaphson及Landweber算法;且选择LBP、Tikhonov正则化作为不同迭代初值时,本文算法相比于Landweber算法具有初值不敏感性,更有利于ECT实际工业应用;并分析了不同算法、不同初值对各流型的影响,进而说明本文算法的有效性及实用价值。
1 ECT关键问题
1.1 ECT正问题
ECT正问题是指根据介质的介电常数分布与电容敏感场的边界条件,利用特定的数学模型求解场域内电磁分布,从而获取各电极对之间的所有电容值[15]。根据静电场Laplace方程,将正问题表示为:
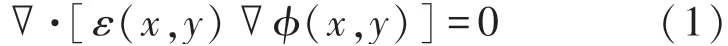
式中:ε(x,y)为(x,y)处的介电常数分布,φ(x,y)为(x,y)处的电位分布。ECT正问题采用Dirichlet第一类边界条件,相应表达为:
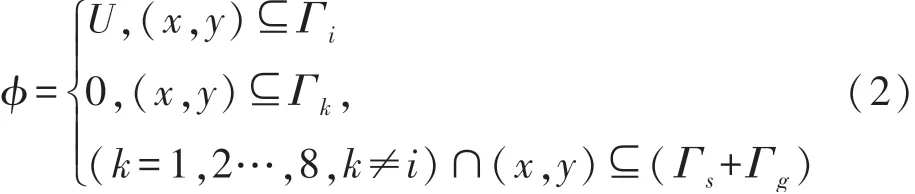
式中:U为边界激励电压;Γi为电极i所在的空间位置;Γs为屏蔽层的位置;Γg为保护电极位置。在已知边界条件的前提下,求出在对电极i添加激励时j电极上存在的电荷,计算公式为
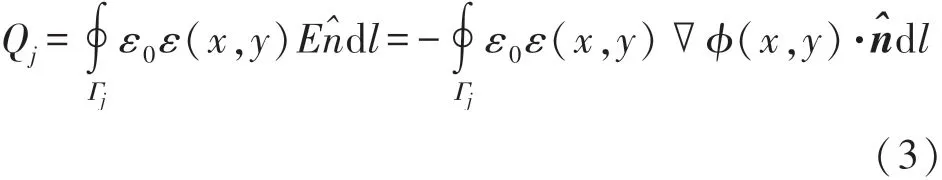
式中:Γj为包围电极j的封闭曲线,E为电场强度,^n为Γj上的法向量。激励电极i和检测电极j之间形成的电容为:

式中:U ij为电极板i与j之间的电压。由于ECT介质分布复杂、非线性等特性,常通过有限元法完成敏感场的剖分及相关数值计算,本文选用三角形剖分单元,剖分结果如图1所示。

图1 ECT传感器场域的三角形剖分图
1.2 ECT反问题
ECT反问题即图像重建,根据正问题得到的电容测量值结合灵敏度矩阵,通过计算机图像重建单元反演出场域内不同介质的介电常数分布图像[16]。电极对间的电容值与介质的介电常数分布存在非线性关系:

将上式进行Taylor展开,忽略高阶项,并对其离散化、归一化可得:

式中:λ为m维归一化电容向量,本文m=28,即所有电容值数量;S为m×n维归一化灵敏度矩阵,g为n维归一化介电常数向量。
1.3 Landweber算法
Landweber迭代算法的基本思路是将ECT反问题的求解转化为求目标泛函极值的优化问题。将式(6)转化为如下目标泛函:
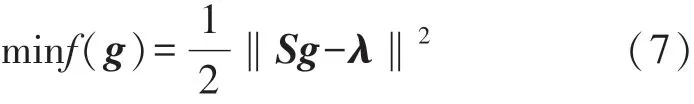
相当于求式(8)的极小值

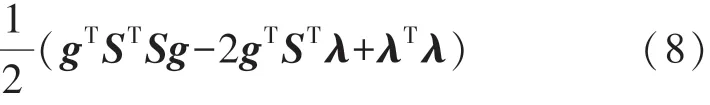
f(g)的梯度为:
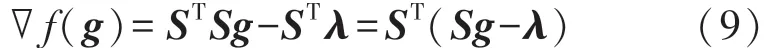
Landweber算法格式为:
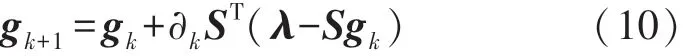
式中:∂k为迭代步长。
1.4 基于权重因子Landweber算法
从数学级数角度分析Landweber算法,假设A0为S-1的初始近似矩阵,令I为单位矩阵,构建残差矩阵P:

如果S-1存在,则可将式(11)写为:
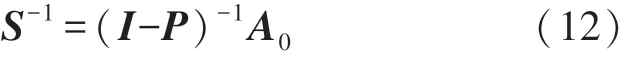
若残差P的谱半径ρ(P)<1,则将(I-P)-1级数展开,S-1的第k项级数A k和第k+1项级数A k+1可分别写为:
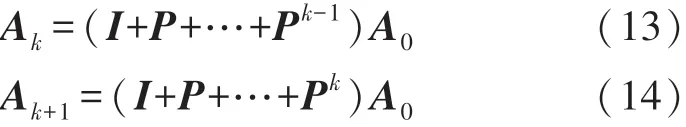
又因为
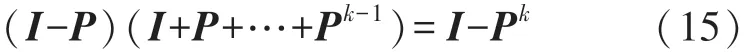
根据式(11)、式(13)、式(15)可得:
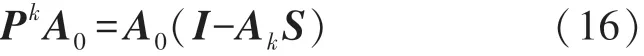
若以S-1第k+1项级数A k+1代替S-1,并结合式(13)则有下式成立:
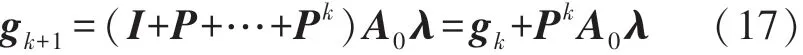
将式(16)代入式(17)得:

若令A0=∂k ST,则式(18)可写为:
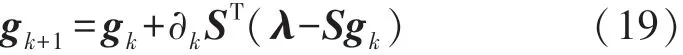
式(19)为Landweber算法的迭代公式,按级数理论,Landweber算法的稳定收敛条件为:

由于STS是一个对称、非负定矩阵,(I-∂k STS)2的特征值中必定包含1,即ρ(P)≥1。故Landweber算法不能满足稳定收敛条件。为解决Landweber算法此问题,构造新算子,令A0=W∂k ST:

式中:W为权重因子,其选择依据是1,经实验对比,W∈(1,1.8)较为理想。将改进后的算子P′替换式(17)中原算子P,可得

1.5 改进Landweber算法
Frozen Landweber迭代是将萨马斯基技巧应用到Landweber中,针对非线性不适定
问题F(x)=y,得出迭代公式如下:

由上述理论可知,ECT重建算法中的电容向量λ和图像分布向量g之间存在非线性关系为式(6),故用灵敏度矩阵S取代F′(g),Sg取代F(g),再结合式(22),则式(23)可改写为本文改进Landweber算法:

算法流程图如图2所示。

图2 算法流程图
2 仿真实验
2.1 不同算法对比实验
为定量描述Landweber算法、NewtonRaphson算法及本文算法的成像质量,采用重建图像的相对误差(Relative Error,RE)及相关系数(Correlation Coefficient,CC)作为两项客观评价指标。其计算公式如(25)与(26)所示:

式中:g表示通过图像重建算法获得的介电常数分布为管道内真实介电常数分布分别为g和^g的平均值,D为g和的维度。
图像重建的有效性由迭代次数、算法的稳定收敛性及其对应的相对误差和相关系数体现,迭代次数的选取由数值实验确定。为直观验证本文算法的有效性及迭代次数对算法的稳定性和重建图像质量的影响,选取常见的四种流型:层流(a)、环流(b)、芯流(c)以及泡流(d)。经反复实验分析,绘制以5步为间隔取100次迭代内Landweber算法、Newton-Raphson算法及本文算法在不同迭代次数下各流型的相对误差及相关系数曲线(图3~图6)并分析算法的稳定性和有效性。

图3 流型a相对误差和相关系数

图4 流型b相对误差和相关系数
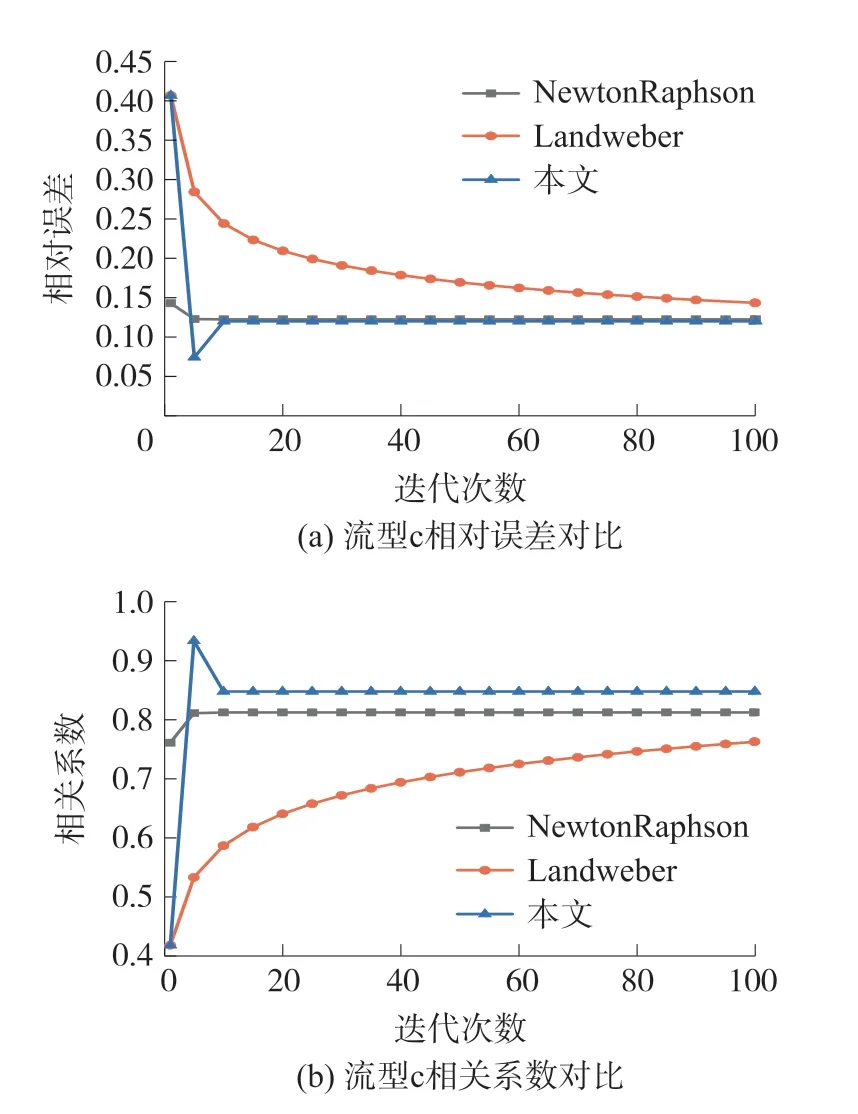
图5 流型c相对误差和相关系数

图6 流型d相对误差和相关系数
由图3~图6可见各算法对各流型在100次迭代内的稳定收敛性,对于流型a、b本文算法均迭代10次达到收敛,NewtonRaphson算法迭代15次收敛,且本文算法的相对误差和相关系数得到明显改善;对于流型c本文算法及NewtonRaphson算法分别迭代10、15次达到收敛,且本文算法的相关系数有一定程度的提升,能够在迭代5次时达到最优;对于流型d本文算法在迭代10次快速趋于稳定,与NewtonRaphson算法相比,两种算法的客观评价指标达到最优时相差范围大概分别为0.027 6、0.041 5,故本文算法具有一定的准确度;对于流型a、b、c、d本文及NewtonRaphson算法较Landweber算法都能达到稳定收敛状态,且本文算法对于各流型均在迭代10次较快达到收敛,收敛速度明显优于NewtonRaphson算法和Landweber算法,体现本文算法的快速收敛性。
为客观比较不同算法的成像效果,将各算法分别迭代100次对4种典型物场分布进行图像重建如表1。
由表1可见,LBP算法只能粗略反映介质分布形状;NewtonRaphson算法能大致反映重建图像的边缘信息,略优于LBP,但存在内部伪影较多;Landweber算法在一定程度上改善了主观成像质量,总体成像效果优于前两种对比算法,但仍存在部分失真;本文算法能较清楚的反映各介质分布的内部和边缘信息,与原始图像更接近,成像效果较佳,只是对流型d仍存在一定程度的边缘失真,还有待改进。综上,经实验对比分析本文算法对各流型的主观仿真效果与客观数值模拟结果一致且具有稳定收敛性,表明本文算法对ECT成像具有较好的重建能力。

表1 各算法图像重建结果
2.2 不同初值对比实验
不同算法的性能由其稳定收敛性直观体现,在实际工业应用中,ECT图像重建算法的稳定收敛性受到初值选择的直接影响。由上述实验可知对4种流型在100次迭代内,NewtonRaphson算法和本文算法在迭代后期均趋于稳定,而Landweber算法对于各流型在迭代后期相对误差呈下降趋势、相关系数呈上升趋势,故为进一步比较本文算法与Landweber算法稳定收敛性及初值选择对二者的影响,成倍增加迭代次数,分别以LBP、Tikhonov正则化为初值,10倍为间隔取100~105内的客观评价指标实验结果并绘制图7、图8(层流、环流、芯流、泡流分别表示为a、b、c、d)。

图7 以LBP为初值各流型相对误差和相关系数对比
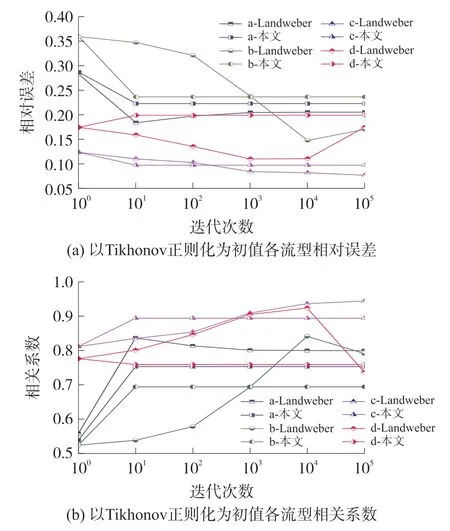
图8 以Tikhonov正则化为初值各流型相对误差和相关系数对比
通过对比图7、图8,无论选择LBP算法还是Tikhonov正则化作为初值,对于各流型Landweber算法的相对误差和相关系数整体波动性较大,整体稳定性较差,故对初值较敏感;而本文算法对各流型的客观评价指标均仅迭代10次时就快速达到稳定收敛状态,迭代速度和稳定性不随初值选择而改变,算法性能明显优于Landweber算法,可见本文算法对初值选择的不敏感性,更具有工业实用价值。为进一步验证本文及Landweber算法对各流型初值选择的影响,将a、b、c、d四种流型分别以LBP、Tikhonov正则化为初值各迭代10次,绘制客观对比图9。
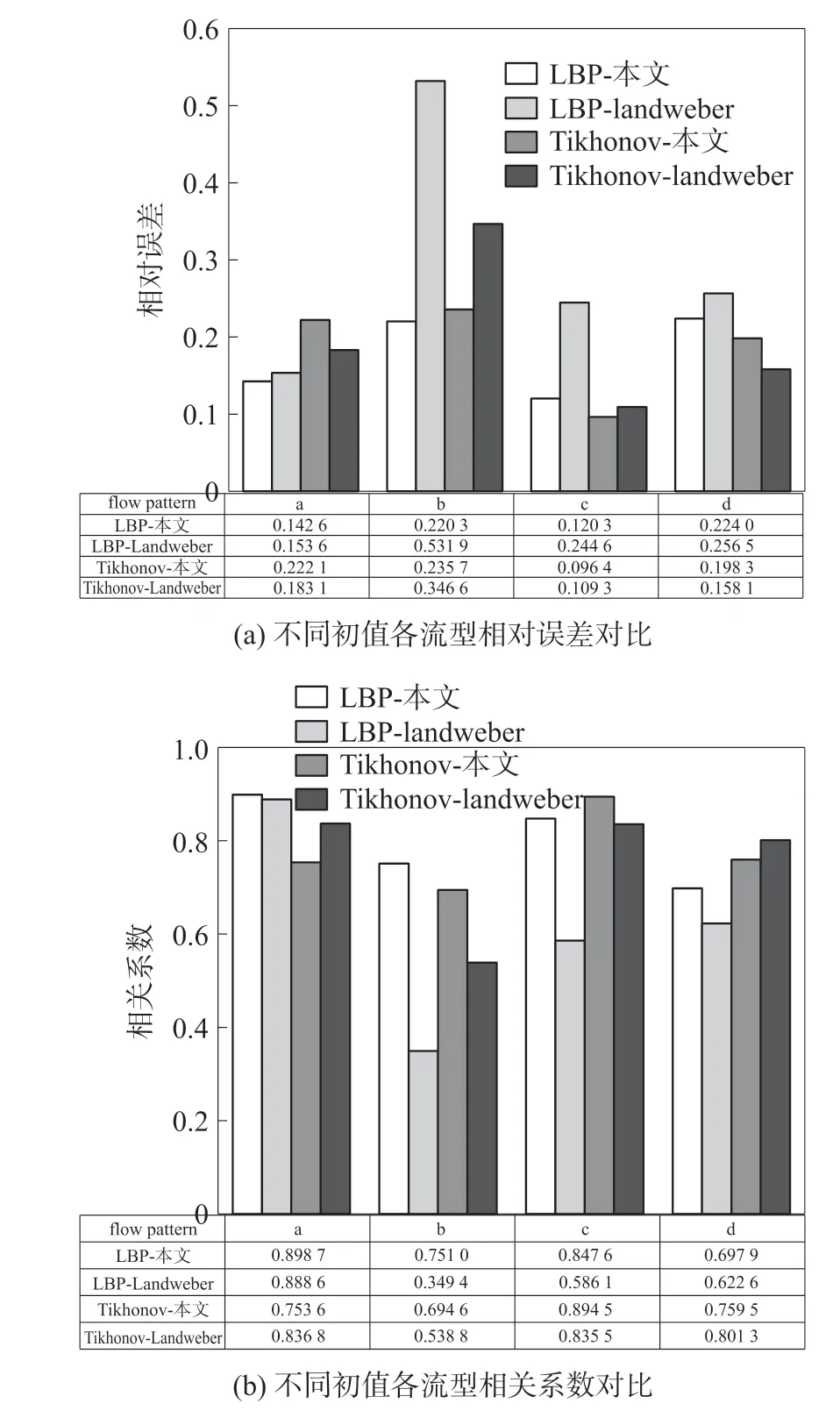
图9 不同初值各流型相对误差和相关系数客观对比
由图9客观对比分析可知对4种流型,选择以LBP算法为初值时,本文算法较Landweber算法客观评价指标更优;相对比而言以Tikhonov正则化为初值时对流型a、d,Landweber算法的客观性指标稍优于本文算法5%左右;对于流型b、c,本文算法的相对误差和相关系数均优于Landweber算法。整体而言,选择不同初值时本文算法一定程度上优于对比算法,从而验证了初值选择对本文算法的影响。
3 结论
电容层析成像(ECT)技术中反问题(即图像重建)属于一类非线性不适定问题,不易对其进行直接 求解,常将其转化为求目标泛函极值的优化问题,再利用 Landweber算法求解。本文针对Landweber算法迭代次数较多、半收敛性等问题,根据Frozen Landweber格式,将萨马斯基技巧应用到基于权重因子的Landweber算法中,提出一种改进电容层析成像算法,加快了稳定收敛速度。经数值仿真实验验证,改进算法的客观评价指标和主观图像重建质量均优于 NewtonRaphson算法和Landweber算法,且改进算法具有初值不敏感性,不同初值对各流型的相对误差和相关系数均仅迭代10次时就达到稳定收敛,验证本文算法的有效性,最后论证了不同算法、不同初值对4种流型的影响,体现本文算法的实用价值。

