一种基于单纯形法的自适应均衡优化算法*

刘紫燕梁水波袁 浩孙昊堃梁 静

(贵州大学大数据与信息工程学院，贵州 贵阳 50025)

近年来，元启发式算法由于其简单性、灵活性和较高的鲁棒性，已经被广泛应用于解决越来越多的工程问题。一般来说，元启发式算法模拟自然现象建立数学模型，元启发式算法主要包括进化算法、群体智能算法和物理现象算法。

基于进化的算法受达尔文进化论的启发，保留了种群中最好的个体作为后代来执行相关操作。基于进化的算法主要包括遗传算法(GA)[1]、进化策略(ES)[2]、差分进化策略(DE)[3]。基于群体智能的算法模拟生物群体中的智能行为来建立数学模型，如觅食方式、迁徙路线、交配选择和信息共享机制等。此类算法主要包括粒子群算法(PSO)[4]、灰狼优化算法(GWO)[5]、蚁狮优化算法(ALO)[6]、鲸鱼优化算法(WOA)[7]、麻雀搜索算法(SSA)[8]、蝴蝶优化算法(BOA)[9]等。基于物理现象的算法受到物理现象的启发，主要算法包括黑洞算法(BH)[10]、引力搜索算法(GSA)[11]、均衡优化算法(EO)[12]等。

均衡优化算法是学者Afshin Faramarzi受控制容积质量平衡物理现象启发而提出的一种优化算法。Yang等人[13]对风光新能源参与调控的电网无功优化进行建模，采用均衡优化算法进行无功优化求解得出最优的组合方案。Wunnava等人[14]针对基本的均衡优化算法的搜索空间中不良粒子随机分散问题，提出了一种根据适应度值自适应决定的改进均衡优化算法。Gupta等人[15]利用高斯变异和基于种群划分和重建概念的附加探索性搜索机制来改进基本均衡优化算法，并应用到实际的工程问题中。

但是上述算法并未考虑到均衡算法易受局部极小值影响的、多样性低、收敛速度慢的问题。本文提出了一种改进的均衡优化算法，算法主要利用Sin混沌映射来初始化种群以增加算法的搜索能力；采用非线性自适应权重策略，以便搜索代理可以自适应的探索搜索空间，平衡开发和探索阶段；在算法的搜索过程中，通过单纯形法的反射、扩张和收缩运算对较差位置的代理进行改进。最后，通过10个基准函数及其Wilcoxon秩和检测和部分CEC2014测试函数的仿真实验结果对比了改进的均衡优化算法与其他智能优化算法的性能，验证了所提算法的有效性。

1 均衡优化算法

1.1 算法背景

均衡优化算法(EO)是一种基于控制体积质量平衡模型的新型元启发式算法，其利用通用质量平衡方程来研究控制体积中非反应性成分的浓度，质量平衡方程体现了控制容积内质量进入、离开及生成的物理过程，一般采用一阶微分方程来描述，公式如式(1)所示:

式中:V为控制容积，VdC/dt代表控制容积的变化率，C代表控制容积的浓度，Q为进出控制容积的容量流率，Ceq表示期望为全局最优的平衡状态下的浓度。G是控制容积内的质量生成速率。式(1)是时间相关的方程，因此当VdC/dt达到0时，可以达到稳定的平衡状态。VdC/dt可以被简化为Q/V，定义为流动率λ，因此，式(1)可以重新组合为式(2)。

对式(2)两边取积分得式(3):

通过求解式(3)可得:

式中:F为指数项系数，C0控制容积在时间t0的初始浓度。

1.2 算法优化原理

EO主要基于式(4)进行迭代优化。算法的具体操作过程和参数设计如下。

初始化 在迭代次数iter＝1时，使优化变量在一定的上限和下限范围内随机初始化，如式(6)所示:

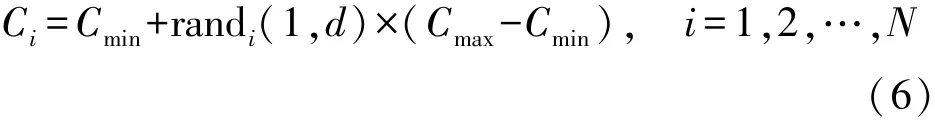
式中:N是优化变量的数量，Cmin表示第i个候选解，Cmin、Cmax分别为优化变量的下限向量与上限向量，randi是d维随机向量，每个元素值均为0～1的随机数。根据式(6)初始化候选解方案后，使用式(7)进行迭代更新位置。

指数项系数F向量F i t＝a1sign(r－0.5)(eλi t t－1)被称为指数项系数，旨在搜索过程中保持开发和探索之间的平衡。其表达式如式(9)所示:

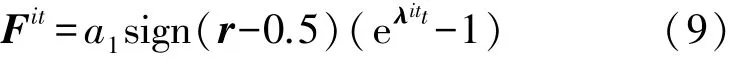
式中:a1是控制全局探索能力的值，a1的值越高，算法的全局探索能力越高，反之，则越低。sign为符号函数，r、λ均代表维度与优化空间维度一致的随机数向量，其值均为0至1的随机数。

质量生成速率G i生成率G i是EO中的主要因素之一，会影响算法局部寻优能力，该参数的定义如下:

2 改进均衡优化算法

2.1 Sin混沌化初始种群

群智能优化算法的种群初始化方法会影响算法的收敛速度和求解精度。EO算法利用随机生成的数据作为初始信息，减少了算法的多样性和整体优化效果。由于混沌运动具有随机性、规律性和遍历性[16]，在求解函数优化问题时，这些特性使算法更容易摆脱局部最优解，从而保持种群多样性并提高全局搜索能力，因此可以用来代替随机初始化。文献[17]验证了Sin混沌与Logistic混沌相比具有更明显的混沌特性，本文采用采用Sin混沌对EO算法进行种群初始化。式(12)为Sin混沌映射的表达式:

为了防止在[－1，1]之间产生不动点和零点，式中的初始值不能取0。

2.2 非线性自适应权重

局部开发和全局探索作为优化算法的两个重要阶段，过度的开发能力会抑制搜索代理向全局最优解发展的趋势，过多的探索能力会降低优化精度。因此，在两个阶段之间找到合适的转换可以提高优化算法的性能。均衡算法中的a1的变化直接影响搜索和开发之间的平衡，从而影响算法的性能。但是a1的值是在原算法中是经验设定的且为固定值，从而导致EO算法具有随机性和局限性。

本文采用非线性自适应权重，可以通过迭代次数自适应的调整参数a，以减少随机性对算法的影响，所提出的非线性自适应权重a通过式(13)表示:

式中:amin、amax分别为收敛因子的最小值和最大值，t为当前迭代次数，T为总迭代次数，gammaincinv为逆不完全伽马函数。如图1所示，非线性自适应权重a非线性地从2递减到最小值amin，在算法迭代前期，种群全局搜索最优解，此时应该给予足够的搜索空间发散种群，因此给予一个较大的收敛步长有利于算法的开发；在算法迭代中后期，算法逐渐收敛，个体开始进行局部搜索，此时给予一个较小的收敛步长有利于算法进行局部探索。

图1 权重系数改进前后对比

因此，在式(7)中引入非线性自适应权重后，可以有效平衡探索和开发，更新方程变换为如式(14)所示:

2.3 单纯形法

单纯形法是指在空间中构造一个多面体，找出该多面体每个顶点的适配度并进行比较，找出最佳、次最佳和最差，通过反射、收缩、扩张等操作更新最差，形成一个新的多面体。它是一种局部搜索方法，具有使用方便、适用范围广、收敛速度快等特点。如图2所示，设最优点为X G，次优点为X B，X C为最优点X G与次优点X B的中心，对于一个最差点X S，g是X S到除X S以外的所有顶点的质心X的方向向量，反射、收缩、扩张运算如下:

图2 单纯形法的四种操作

反射运算:X R＝X C＋α(X C－X S)，X R是执行反射运算后的点，即反射点，X E＝X C＋γ(X R－X C)为反射系数，通常X E＝X C＋γ(X R－X C)。

扩张运算:X E＝X C＋γ(X R－X C)，X E是执行扩张运算后的点，即扩张点，γ为扩张系数，通常λ＝2。

内收缩运算:X W＝X C－β(X S－X C)，X W是执行内收缩运算后的点，即内压缩点，β为内收缩系数，通常β＝0.5。

外收缩运算:X T＝X C＋β(X C－X S)，X T是执行外收缩运算后的点，即外收缩点，β为外收缩系数，通常β＝0.5。

本文利用单纯形法的反射、扩张和收缩运算对当前较差个体进行改进，增加算法跳出局部最优的能力。

2.4 改进均衡优化算法步骤

根据以上策略描述，以下为SMEO的具体步骤:

①设置算法参数:种群规模N、维度d、参数a1、amin、amax、最大迭代次数T、反射系数α、扩张系数γ、内外收缩系数β。

②利用Sin混沌初始化个体。

③计算每个个体的适应度值并根据式(7)确定当前平衡状态池状态。选出当前最优的三个位置为Xα、Xβ、Xδ，对应的适应度值为f(Xα)、f(Xβ)、f(Xδ)。中心位置为X C＝(Xα＋Xβ)/2。

④对最差的位置X S进行反射操作，得到反射点X R。

⑤如果f(X R)＜f(Xα)，即反射的方向正确，将执行扩张操作得到f(X E)，若f(X E)＜f(Xα)，则用X E代替X S；反之，则用X R代替X S。

⑥如果f(X R)＞f(X S)，即反射方向不正确，需执行外收缩操作得到X T，若f(X T)＜f(X S)，则用X T代替X S。

⑦如果f(Xα)＜f(X R)＜f(X S)，执行内收缩操作得到X W，若f(X W)＜f(X S)，则用X W取代X S，反之，则用X T代替X S。

⑧根据式(14)更新其他个体的位置。

⑨判断算法是否满足结束条件，若满足，则算法结束；否则，执行步骤③。

3 改进均衡优化算法实验结果及分析

3.1 基本测试函数

为了验证本文改进均衡优化算法(SMEO)的有效性，采用国际上通用的10个经典测试函数进行仿真实验，均来自CEC2005测试集。这些测试函数分为三类:单峰、多峰和组合函数。

函数f1－f6是只有一个全局最优值的单峰函数，单峰函数用于评价算法的局部搜索能力和收敛速度。函数f7－f9是多峰函数，与单峰函数不同，多峰函数具有多重局部最优解，随着问题规模的增大，局部最优解的数目也会增加。多峰函数对于评价算法的探索能力具有重要的参考价值。f10是复合函数，与多峰函数的不同之处在于它的维数较少，局部最优值较少，并且不允许维数调整，用于测试算法的优化精度。基准函数和特定信息如表1所示。

表1 基准测试函数及详细信息

3.2 仿真平台及参数设置

本文的仿真实验操作系统为Microsoft Windows 10，CPU为Intel Core i7，主频为2.4 GHz，内存为8 GB。实验编程软件为MATLAB R2017b。

算法参数设置:算法种群规模设置为30，最大迭代次数为500，维度为30，各基本算法内部参数设置如表2所示。

表2 算法参数设置

3.3 与不同改进EO算法对比

使用10个不同的基准测试函数分别对EO、SMEO、AEO[14]以及m-EO[15]进行求解，通过对4种算法的平均值和标准差的统计来对比验证SMEO算法的有效性。算法独立运行30次，实验的平均值反映了算法在给定迭代次数下的收敛精度，标准差反映了算法的稳定性。实验结果如表3所示，其中加粗的部分为最优结果。

从表3可以看出，本文提出的SMEO算法在10个基准测试函数上均取得了不错的寻优效果。对于函数f1、f2、f3、f4、f7、f9，SMEO算法相对于其他三种算法，算法准确度显著提高的同时，且收敛到理论最优值0，说明搜索效果得到了很好的提升。对比函数f7，四个算法均收敛到理论最优值。m-EO算法在函数f5上取得最好的效果，更加的接近理论最优值。对于在10个基准函数上的表现效果，SMEO算法在9个函数上优于EO算法，在8个函数上优于AEO，在8个函数上优于m-EO算法。综合上述比较结果来说，与EO算法、AEO算法以及m-EO算法相比，SMEO算法达到了更高的求解精度和取得了更好的稳定性。

表3 不同EO算法对10个测试函数的实验结果

3.4 与其他智能优化算法对比

为了进一步评估改进SMEO的性能，将本文的SMEO算法与鲸鱼优化算法(WOA)、灰狼优化算法(GWO)、麻雀搜索算法(SSA)、蝴蝶优化算法(BOA)进行比较，实验结果如表4所示，在10个基准测试函数上的收敛曲线如图3所示。

表4 不同智能算法对10个测试函数的实验结果

图3 各测试函数下的收敛曲线

从图3可以看出，本文SMEO算法在10个测试函数中的收敛曲线明显优于其他的算法函数，特别是在f1、f2、f3、f4、f6函数中，在适应度值达到最低的同时收敛速度也远优于EO算法、GWO算法、SSA算法、BOA算法，说明本文提出的改进策略可以有效地提高EO的局部开发能力和收敛速度。对于多峰函数f7、f8、f9，SMEO在200次迭代内找到最优值并退出迭代，收敛曲线表明，SMEO算法可以避免算法陷入局部最优，并具有强大的全局搜索能力。

从表4可以看出，SMEO算法在f1、f2、f3、f4、f6、f7、f8与f9等8个基准测试函数上均取得了最优的最优值、平均值以及标准差EO在f5与f10上取得最优的效果。

为了进一步地验证SMEO数据的可靠性和有效性，本文采用Wilcoxon秩和检验[18]对实验结果进行进一步分析。Wilcoxon秩和检测常用来对比两组数据之间的差异，以确定它们是否在统计上存在显著不同。本文将EO算法、GWO算法、SSA算法、BOA算法与SMEO算法在10个基准测试函数上进行Wilcoxon秩和检验对比分析，验证SMEO算法寻优结果在统计学上的优势。若计算出P＜5%，可以认为是拒绝零假设的有利依据，即两个样本数据的差别显著。表5所示为不同测试函数下秩和检验的P值，表中的＋、－与＝分别表示SMEO算法的秩和统计结果优于、次于和等于对比算法，NAN表示检验的所有样本数据相同，即算法的性能相当。

由表5结果可知，除了算法性能相当的以外，SMEO算法相较于其他算法的Wilcoxon秩和检测结果P值基本上都小于5%，说明SMEO算法对于基准测试函数的优化结果在统计学上的具有很大的优势，验证了SMEO算法的鲁棒性。

表5 测试函数下秩和检验的P值

3.5 CEC2014测试函数寻优对比

为了进一步验证SMEO算法处理具有复杂特征的问题时的鲁棒性，本文选取部分具有复杂特征的CEC2014单目标优化函数进行寻优对比分析，其中包括单峰(UF)、多峰(MF)、混合(HF)和复合(CF)类型函数，函数相关信息如表6所示。本文将SMEO与标准EO算法、GWO算法、L-SHADE算法、SSA算法、WOA算法进行对比。其中，L-SHADE算法在CEC2014测试函数中表现卓越，常用做于对比实验。实验参数取种群规模为N＝50，维度d＝30，最大迭代次数为2 000，每个函数独立运行50次取平均值和标准差。其中L-SHADE算法的数据来源于文献[19]，SMEO算法运行结果及与其他算法对比如表7所示。

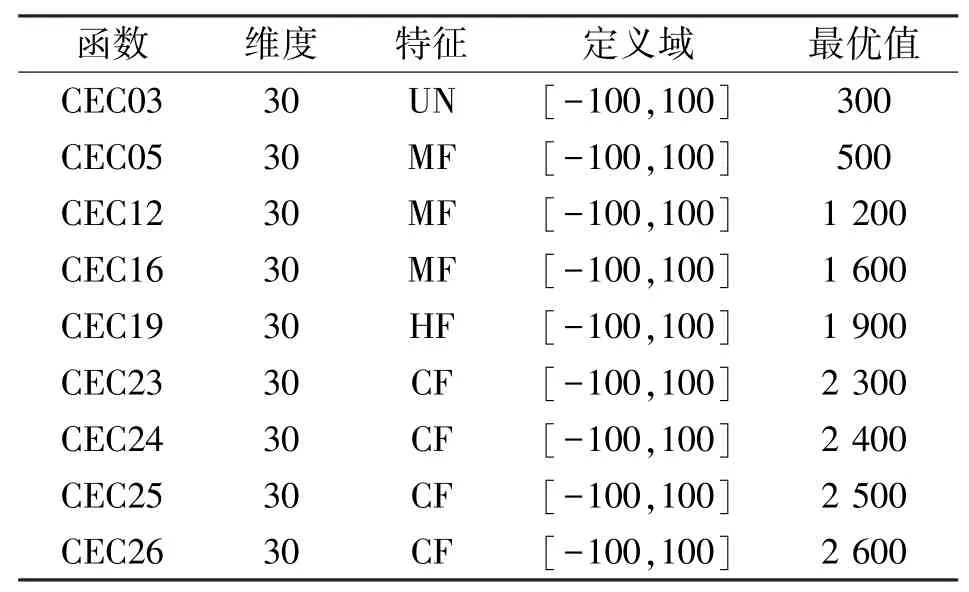
表6 部分CEC2014函数

表7 CEC2014函数优化对比

从表6可以看出，SMEO算法在CEC2014测试函数上的优秀表现，除了单峰CEC03函数，SMEO算法在其他8个测试函数上都取得了最优精度。对于CEC12、CEC13、CEC16以及CEC19测试函数，SMEO算法基本收敛到了理论最优值；对于复合特征CEC23、CEC24和CEC24函数，SMEO算法寻优标准差为0，说明其对于复合特征函数寻优稳定性很高。上述CEC2014测试函数寻优结果分析说明，本文提出的SMEO算法对于具有复杂特征的函数寻优上同样具有很大优势，验证了SMEO算法的鲁棒性。

3.6 SMEO算法时间复杂度分析

SMEO算法的计算复杂度主要有两部分:第一部分是基本EO的复杂度为:

式中:d为变量维数；第二部分单纯形搜索的计算复杂度为O(d×g(d)×tmax)，其中g(d)为计算适应度值的次数。因此，整个SMEO算法的复杂度为:

虽然SMEO算法的复杂度比基本EO算法大，且都在同一数量级，但是所提算法的求解精度和稳定性都要比基本EO算法好。

4 结论

本文为了进一步解决EO收敛速度慢，易陷入局部最优的问题，提出了三种改进策略，即Sin混沌初始化、非线性自适应惯性权重以及单纯形法。利用10个基准函数和部分CEC2014测试函数进行实验比对，提出的策略对收敛速度和精度得到有效提高。同时，为了验证SMEO的可靠性和有效性，对已给出的数据进行统计检验作出性能评价分析。校验表明，改进的算法在搜索精度、误差分析和成功率整体都要优于其他算法，鲁棒性也得到提高。下一步工作考虑将SMEO应用于实际工程设计问题，进一步验证SMEO算法相对于其他算法的优越性。