冲击作用下节理岩体应力波波速衰减规律研究
潘珍颖, 刘 军, 甄梦阳
(1.河海大学土木与交通学院,南京 210098; 2.河海大学岩土力学与堤坝工程教育部重点实验室,南京 210098)
随着经济发展,对岩体的机械开挖和老旧建筑的拆除越来越多,而机械开挖、拆除爆破等实际工程中产生的振动不可避免地会对岩体和周边建筑产生动态干扰,存在安全性和稳定性的隐患. 节理是岩体中常见的一种软弱结构面,节理岩体广泛存在于实际工程中,其中节理不仅会影响岩体的力学性能,也会造成应力波的衰减. 通过研究应力波在节理岩体中的振动衰减规律,有助于指导实际施工. 冲击荷载下节理对振动衰减规律的影响受到国内外学者的重视,在理论研究方面,Cai和Zhao[1]将特征线法与位移不连续模型相结合,结合两者优势求解出节理面前后振速数据;刘婷婷等[2]、刘立波等[3]基于不同的理论方法对节理刚度、间距、数量以及应力波幅值、频率多个参数展开分析. 试验研究方面,Yu等[4]、Han 等[5]、李圳鹏等[6]采用霍普金森压杆试验研究不同节理厚度的节理岩体在不同冲击速度下的应力波传播规律;李业学等[7-9]通过SHPB动力加载试验分析了应力波穿过节理岩体时的能量耗散过程和机理,并基于损伤力学的基本理论和线性位移不连续模型,推导了应力波在节理岩体中传播波速的解析解;邓显石[10]、曾晟等[11]、陈道龙等[12]利用水泥砂浆制备了完整岩体试件和不同形式节理岩体试件,通过落锤式冲击试验机对不同贯通度、不同倾角及不同组数的节理岩体进行不同加载速率和次数的动力压缩试验,阐明了不同几何形式节理岩体的动态力学特性;孙冰等[13-14]基于Froude 相似比例法制作了层状节理岩体模型,通过落锤试验装置,利用离散快速傅里叶变换对不同位置的加速度时程信号进行频域分析,发现节理的滤波作用表现为低通滤波性;夏致晰等[15]针对爆炸应力波穿越层状岩体界面上的透反射关系及在各岩层的衰减特征进行分析研究;田振农等[16]利用摆锤装置研究了一维应力波在岩体中的传播规律,发现随着结构面组数增加,质点振动衰减加快,应力波随距离的衰减明显;杨涛等[17]通过3D打印制作不同倾角的六棱柱形节理试件,研究分析节理岩体强度随节理倾角变化的各向异性特征. 数值模拟方面,任梦等[18]利用有限元软件分析了应力波通过贯通节理的传播规律,并与已有的位移不连续理论结果进行对比;李秀虎等[19]、周能娟[20]、张凤鹏等[21]利用动力有限元软件LS-DYNA 对不同节理填充物强度、物性的节理岩体进行数值模拟分析,发现应力波传播规律受节理填充物性质的影响明显.
综上,目前对应力波在节理岩体中的衰减规律的研究多是针对节理岩体内部的,不能准确地反映表面振动响应. 然而,节理岩体对表面振动响应的研究可以更好地分析节理对应力波波速的衰减规律,为实际作业时冲击荷载产生的地表振动研究提供参考. 因此,本文针对人工填充节理岩体试样在冲击荷载作用下对表面振动响应规律的影响展开研究,用于分析节理对应力波波速衰减规律的影响. 采用自行设计的简易摆锤冲击装置进行了一系列的冲击加载试验,根据测得的梁状结构表面振速数据分析节理存在与否、节理数量和节理厚度对冲击荷载下节理岩体振动衰减规律的影响,并利用特征线法和位移不连续模型推导节理面对振动衰减的影响,将理论解和试验数据进行对比验证. 以期为日后实际工程作业中减小对周边建筑物的安全风险提供一定的参考.
1 位移不连续模型
目前,在开展宏观节理岩体内应力波衰减规律的理论分析时,对于裂隙较少的情况采用位移不连续方法通常可以得到较好的求解效果[22].
位移不连续模型假设节理为两个弹性半空间体的间断面,节理处的应力场是连续的,应力作用下由于自身变形及微小空隙闭合产生的位移场是不连续的. 节理两侧的关系如下:

式中:σ为应力;u为质点位移;n和j为两个变量,其中n为节理编号(n=0为岩体边界,n=1,2…,依次为入射波经过的第一个结构面、第二个结构面…),j为经过n个节理后所需的时间间隔数量;上标+和-分别代表节理前和节理后.
位移不连续模型假设节理为无厚度的结构面,通过选择合理的节理刚度可以将有厚度节理的影响等效为无厚度节理. 假设节理为各向同性介质,根据轴向变形量计算公式,一般采用下式来表示节理法向刚度和填充物弹性模量、节理厚度的关系:

式中:K(n)为节理法向刚度;E为填充节理的弹性模量;e为节理厚度.
Cai和Zhao[1]采用位移不连续模型与特征线法相结合的方法推导出节理前后粒子振动速度的递推公式,经多学者验证可靠,本文采用该递推公式展开研究.
由于本文中采用的试验节理两侧的岩体材料相同,即节理两侧的波阻抗相同,所以Z(n)=Z+(n)=Z-(n),简化后得到应力波通过任意n条节理后的速度迭代方程:
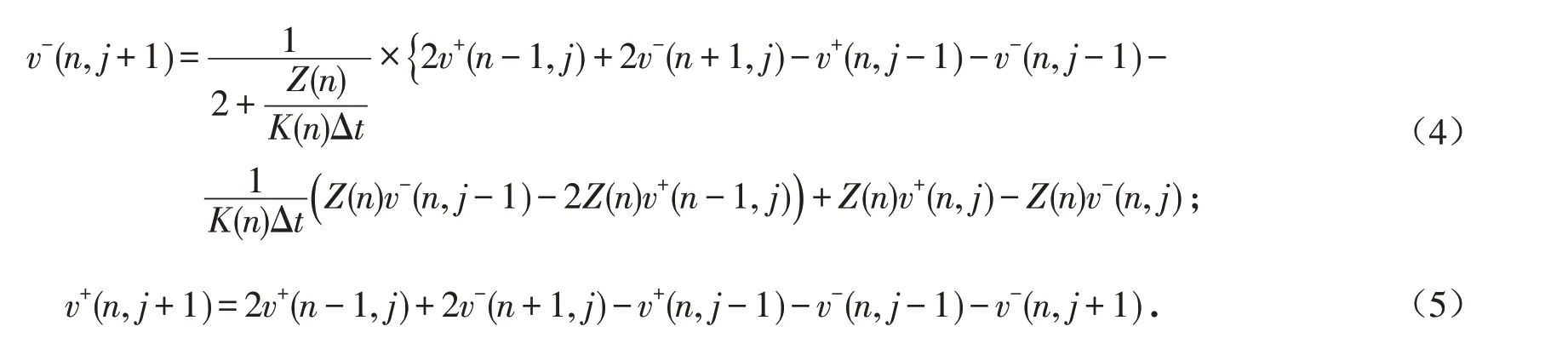
式中:Z(n)表示节理两侧材料的波阻抗,即密度和波速的乘积;Δt代表两节理间的传播时间;v+(n,j+1)和v-(n,j+1)代表在j×Δt时刻的第n个节理两侧的速度.
因此,若求解通过某一节理后的速度v+(n,j+1),只需根据左侧边界速度条件v-(n,0)和初始速度条件v-(0,j)、v+(0,j),通过C++将上式进行迭代计算即可获得.
2 试验研究
振动测试试验是用于研究冲击振动特性的有效手段,本文采用自行设计的简易摆锤冲击装置进行节理岩体的冲击振动响应试验研究.
2.1 试件制备
由于现场取样岩体的节理构造不易辨识,很难开展各节理参数的具体分析,本文选择水泥砂浆材料,采用现浇法自制含人工节理的梁状结构试样模拟节理岩体. 选用C42.5 普通硅酸盐水泥、细度模数为2.3的中砂、自来水配制岩体试样,水泥∶砂∶水配合比为1∶1.6∶0.4. 梁状结构的规格尺寸为200 mm×200 mm×2000 mm(高×宽×长). 为了确定水泥砂浆的物理参数,在进行梁状结构浇筑的同时取搅拌好的水泥砂浆制作标准件,将制作好的梁状结构和标准试件置于同等条件下养护28 d,养护龄期满后测得水泥砂浆的物理参数如表1所示.

表1 水泥砂浆梁状结构物理参数Tab.1 Physical parameters of cement mortar beam structure
所制作的节理倾角皆与冲击荷载方向垂直,即布设平行节理. 具体操作是,在水泥砂浆浇筑振捣后插入不同厚度的大理石板至初凝后取出,即得预制节理,亦可保证各段浇筑后的密度、孔隙度等的近似性.
由于天然状态下的节理部位往往含有一定的填充物,为使试验结果更贴合实际,所以选择黏土来模拟节理部位的软弱薄夹层,所采用黏土的物理参数如表2所示. 制作填充节理时通过控制填充黏土的质量来控制节理中黏土密实度统一.

表2 节理填充物的物理参数Tab.2 Physical parameters of joint fillers
试验的变量因素是节理有无、节理数量和节理厚度. 设置不含人工节理的梁状结构一个,单节理、双节理、三节理梁状结构各五个,每组试件内节理厚度分别取值为2、3、4、5、6 mm,共十六个试件. 含人工节理的梁状结构的设计图如图1所示.

图1 含人工节理的梁状结构设计图Fig.1 Design drawing of beam structure with artificial joints
2.2 试验装置
试验主要通过自研的简易摆锤冲击装置进行冲击加载,利用振动监测仪获取振速数据开展研究. 自行设置的摆锤冲击加载装置,由摆锤起吊装置和摆锤冲击加载装置两部分组成,摆锤重5.2 kg. 固定好起吊装置后,通过人工控制摆锤实现摆动来提供动力源,并通过调控摆锤高度来控制冲击能量,仪器见图2所示.

图2 冲击加载装置Fig.2 Impact loading device
振动监测仪器采用加拿大Instantel公司生产的Minimate Pro4TM型振动和过压监测仪,连接一个ISEE标准或DIN标准三向检波器,仪器见图3所示.

图3 Minimate Pro4TM型振动和过压监测仪Fig.3 Minimate Pro4TM vibration and overpressure monitor
2.3 试验方案
通过自制的摆锤试验装置来提供侧向水平冲击荷载对试样进行冲击试验,试验过程中控制摆锤高度来确保冲击能量相同.
在每个梁状结构的上表面布置四个测点,测点间距离均为500 mm,距离冲击点由近至远分别编号为1#、2#、3#、4#,其中1#和4#分别距离左右端部250 mm,具体位置如图4所示. 通过石膏将振动传感器粘贴在试样上表面测点处,利用Minimate Pro4TM 型振动和过压监测仪来采集各测点的振速响应数据,实物图如图5所示.

图4 测点布设示意图Fig.4 Schematic diagram of measuring points

图5 自制摆锤试验装置实物图Fig.5 Self-made pendulum test device physical drawing
3 试验结果分析
3.1 节理岩体对衰减规律的影响
为研究节理岩体的衰减规律,选取不含人工节理和含三条6 mm厚人工节理的梁状结构进行试验,分别测得四处的振速信息,将各测点的振速时程曲线整理如图6、图7所示.
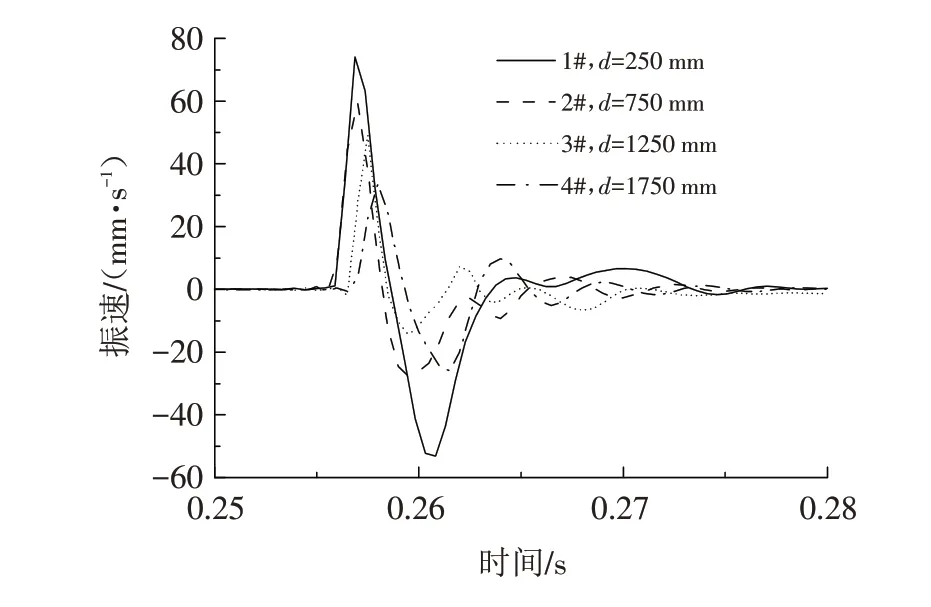
图6 三节理试件各测点振速时程曲线(节理厚度为6 mm)Fig.6 Time history curves of vibration velocities at each measuring point of three joint specimens(joint thickness:6 mm)
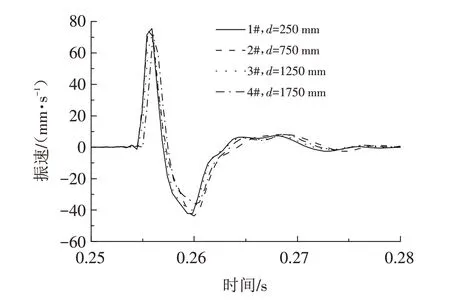
图7 不含人工节理梁状结构的振速时程曲线Fig.7 Time history curves of vibration velocities of beam structure without artificial joints
从图7 可以发现,冲击荷载的振动响应持续时间较短,在短时间内快速达到峰值,随后波动下降,在约0.275 s 以后逐渐趋于稳定. 对比四个测点的振速时程曲线发现,各测点取得峰值大小以及起跳点时间与距冲击点位置紧密相关,由于传播过程中能量不断发散,各测点的振速在整体上呈现出随着距冲击点距离增加依次减小的趋势. 此外,随着距离增大,波形衰减的速度逐渐减慢,呈现出近端衰减快,远端衰减慢,并趋于平缓.
为深入探究节理存在对岩体中应力波衰减规律的影响,选取不含节理水泥砂浆梁状结构试样及节理厚度为6 mm的三种节理数量的试样为例,以四个测点的振速峰值作为研究对象. 随着距冲击点距离的增加,都呈现出振速峰值下降的趋势,但下降幅度不同,这是由于岩体自身和节理两者共同作用的结果,如图8所示. 不含节理梁状结构,振速峰值持续下降,距离和振速峰值近似呈线性相关,每500 mm约衰减1.47 mm/s.单节理梁状结构仅在距冲击点750~1250 mm之间有明显下降,占该试样振速峰值衰减总值的72.589%,双节理试件在250~750 mm 和1250~1750 mm 两段距离均有明显下降,而三节理试件在三段距离均有明显下降,由此发现振速降低明显的部位均存在节理. 更直观地说明了节理和岩体均对应力波的传播起到衰减作用,其中节理的存在能明显加剧应力波的衰减.节理对应力波衰减发挥主导作用,其原因主要是应力波在经过节理时被结构面反射了部分能量,形成能量的一定程度的衰减,且节理填充物也会吸收部分能量.

图8 距冲击点不同距离的振速峰值折线图Fig.8 Line chart of peak vibration velocities at different distances from the impact point
通过该试验分析也从侧面验证了在爆破、开挖等工程中设计减震沟[23-24]来防止施工造成振动危害的合理性,说明减震沟存在确实可以起到很好的降振作用,且通过改变其宽度和数量对其降震效果有所影响.
3.2 不同节理厚度的影响
为研究节理厚度对应力波衰减规律的影响,选取节理厚度为2、3、4、5、6 mm三节理试样,施加相同冲击荷载,对4#测点测得的振速时程曲线进行研究.
如图9所示,各振速曲线峰值依次为58.798、52.498、46.888、38.28、33.758 mm/s. 不含节理梁状结构测得的振速峰值为71.14 mm/s,要远大于含节理梁状结构,且随着节理厚度的增加,振速峰值不断减小,与不含节理梁状结构相比振速峰值降低了17.3%~52.5%. 这是由于节理对应力波波速表现为衰减作用,导致极大程度上削弱了到达试件表面的振动响应.
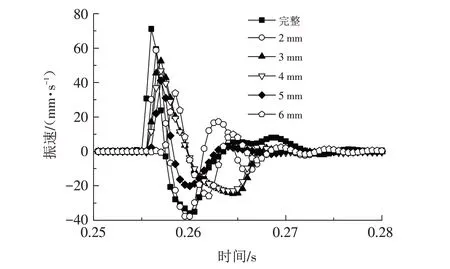
图9 不同节理厚度水泥砂浆梁状结构的振速时程曲线Fig.9 Time history curves of vibration velocities of cement mortar beam structure with different joint thicknesses
节理厚度对振动响应的影响主要是由于节理填充物会吸收部分能量,随着填充节理厚度的增加,吸能效果不断增强,导致振速衰减明显.
为更好地探究应力波振速峰值和节理厚度之间的关系,根据不同节理厚度三节理试样的4#测点测得振速峰值拟合得到图10. 由图10可知,随着节理厚度的增加,振速峰值不断降低,每增加1 mm 振速衰减约6.26 mm/s,由此说明节理厚度对表面振速起到明显的衰减作用.
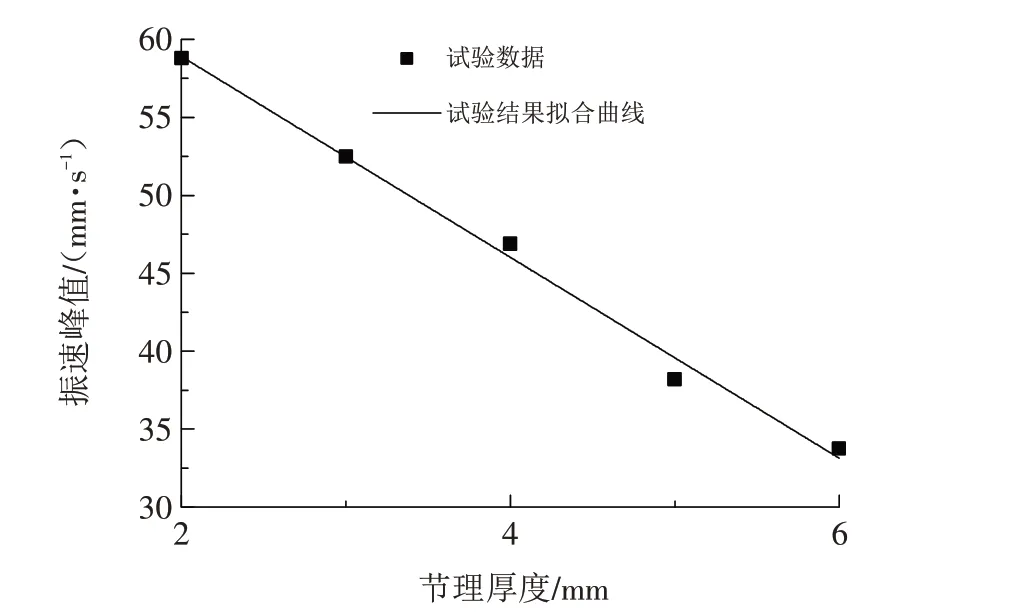
图10 不同节理厚度的振速峰值折线图Fig.10 Line chart of peak vibration velocities of different joint thicknesses
从到达峰值的时间可以发现,节理岩体中到达振速峰值的时间普遍要晚于完整岩体. 所以节理的存在不仅使应力波衰减,还出现延时现象. 这是由于节理填充材料采用的是硬黏土,应力波在其中的传播波速小于水泥砂浆,所以增加了应力波的传播时间,表现为同种填充材料的情况下,节理填充物厚度越大,延时效果越明显.
3.3 不同节理数量的影响
为分析不同节理数量对应力波衰减规律的影响,选择6 mm 厚节理梁状结构4#测点的振速信息进行分析. 由图11可知,不含节理梁状结构和单节理、双节理及三节理梁状结构4#测点的振速峰值分别为71.14、55.62、46.65、33.75 mm/s,无论是单节理还是多节理梁状结构相对于不含节理梁状结构的振速峰值都明显下降,表明在相同冲击荷载作用下,随着节理组数的增加,衰减作用增强,振速峰值逐渐降低,三节理梁状结构降振效果最明显,振速峰值比不含节理梁状结构降低近53%. 造成该情况的原因主要是一方面节理数量增加导致填充材料厚度增加,吸能能力增强,另一方面是结构面增加,结构面的透、反射作用会导致发生复杂的相互作用,能量衰减增大.

图11 不同节理数量的振速时程曲线Fig.11 Time history curves of vibration velocities of different joint numbers
为更直观地定量分析节理对应力波的衰减影响,考虑反射波的作用,将节理前测点1记录的波形作为入射波,节理后测点4记录的波形作为透射波,透射波峰值和入射波峰值之比即为透射系数. 将不含节理、不同节理厚度、数量的梁状结构的透射系数整理如下图12.
由图12可知,透射系数与节理厚度和数量呈负相关. 由于每次试验施加的冲击荷载是一样的,因此测得的入射波大小是近似一致的,透射系数主要由透射波的情况决定,而应力波经过节理时衰减明显,增加节理数量或节理厚度都会加剧对应力波的衰减作用,导致透射系数的减小.

图12 不同节理厚度的透射系数折线图Fig.12 Line chart of transmission coefficients of different joint thicknesses
选取节理厚度为2 mm 的不同节理数量试件,对其透射系数对比分析发现,三者透射系数依次为92.27%、80.93%、77.37%,随着节理数量的增加,透射系数不断降低,但当节理数由1 到2,透射系数下降了12.29%;节理数由2到3,透射系数下降了4.40%,随着节理数量的增加,透射系数降低幅度逐渐减小. 这是由于虽然节理数量的增加会加剧应力波的衰减,但当节理数大于1时,应力波在多条节理间发生多重透反射作用,随着节理数量的增加,透反射作用加强,导致穿过节理组后的衰减程度减小,进而导致透射系数降低幅度减小.
4 理论与试验结果对比分析
为进行理论和试验对比分析,选取节理厚度为6 mm的三节理梁状结构,取1#测点测得的振速信息为入射波曲线,将入射波振速信息带入递推公式通过软件迭代计算后得到透射波的理论值曲线,并将其与试验测得的4#测点振速信息进行比较,曲线如图13和图14.
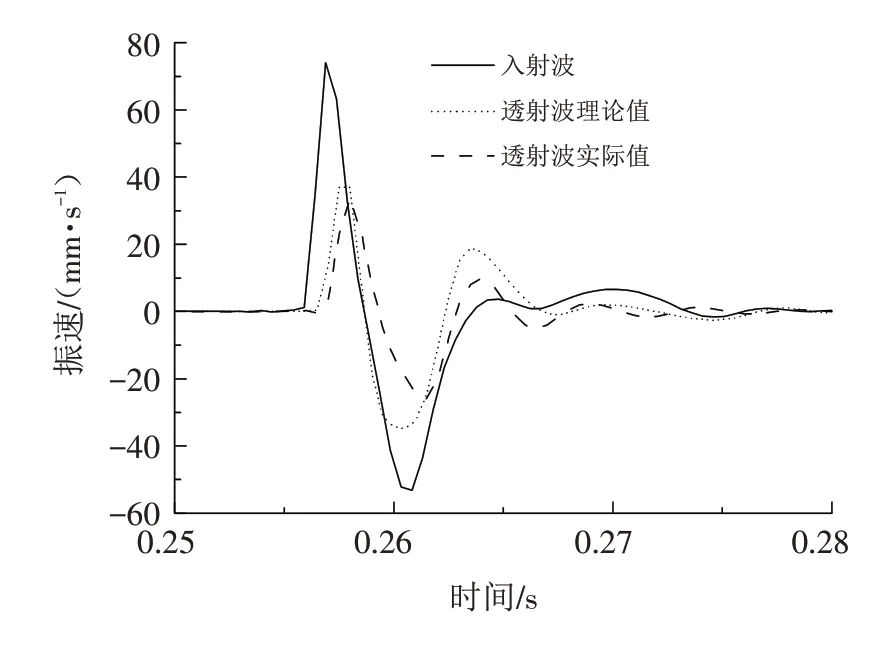
图13 理论与试验透射波振速时程曲线对比Fig.13 Comparison between theoretical and experimental time history curves of transmission wave velocities
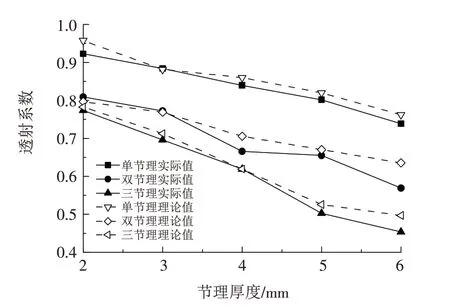
图14 理论与试验透射系数对比Fig.14 Comparison of theoretical and experimental transmission coefficients
由图13对比分析可知,试验结果与理论结果基本吻合,透射波曲线的理论值和实际值的首峰峰值相差3.240 4 mm·s-1,较为相近,到达峰值的时间相近,且两条曲线的波形变化趋势基本一致. 实际值第二个峰的峰值较小,主要原因是由于实际试验时试件制备过程中不可避免会存在气泡以及微裂隙等,而应力波经过时会发生透反射作用,导致应力波发散,而理论分析可以排除这些因素的影响,所以导致有些数据与理论值稍有出入,可以认为理论解和试验分析得到了相同的结论.
不同节理厚度、节理数量的透射系数理论值和实际值如图14所示,理论值和实际值数值结果较为吻合,且两者随节理数量、厚度的变化规律相同. 实测数据求得的透射系数比理论值略小.
5 结论
1)在冲击荷载作用下,随着距冲击点距离的增加,振动响应逐渐减小;节理和岩体都对应力波传播起到衰减作用,但节理能明显加剧衰减.
2)随着节理厚度的增大,透反射现象和填充物吸能效果增强,且节理厚度每增加1 mm振速峰值衰减约6.26 mm/s.
3)随着节理数量的增加,表面的振动响应降低,透射系数降低;节理数量的增加会加剧应力波的衰减,但是由于节理复杂的透反射作用加强导致穿过节理组后的衰减程度减小,造成降低幅度会逐渐减小.
4)理论结果和试验数据基本吻合,由于试件中不可避免地存在气泡、微裂隙等构造存在发散作用,所以实际值比理论值略小.
5)节理岩体的节理数量和厚度均对应力波的传播产生明显的衰减作用,在实际的机械开挖和拆除爆破工程中,通过合理选择地下岩体节理数量和厚度较大的方向开展工作,可以更好地保障周边地表建筑的安全,为工程安全提供一定的参考价值.

