基于三维有限元的异型底板水闸整体稳定性分析

于正洋， 苏静波， 黄绍磊， 刘 睿

（1.河海大学港口海岸与近海工程学院，南京 210098； 2.河南省水利勘测设计研究有限公司，郑州 450016）

水闸是一种在水利工程中应用广泛的低水头水工建筑物，准确评估水闸工程的稳定性具有重要意义.目前常用的计算水闸稳定性的方法包括传统计算方法［1］和三维有限元模拟法. 传统计算方法一般是将水闸与地基分离开来进行计算的，且计算过程采用了大量的简化假设，简化了各结构间的力系传递，忽略了整体效应，因此传统计算方法的计算结果并不能准确反映工程实际情况. 而三维有限元数值模拟法可以将水闸结构与地基视为一个整体进行分析，可同时考虑水闸各结构与地基之间的相互作用，因此利用该方法得出的结果更能准确地反映水闸结构的真实状况. 邹礼兵［2］通过ABAQUS软件对进水闸应力、渗流稳定性等进行了三维有限元模拟分析，经过实际施工验证表明，采用有限元方法进行设计可靠度较高. 钱秋培等［3］应用有限元软件ABAQUS 计算分析了某节制闸的应力及变形，验证了正常蓄水工况下水闸结构的安全性，并且认为传统计算方法的简化处理对水闸结构应力计算的影响较大. 陈立峰等［4］采用ANSYS有限元分析法分析了节制分水闸在不同工况下出现的沉降位移以及应力分布，认为建筑物地基结构整体性与建筑物的稳定性密切相关. 彭兆轩等［5］运用有限元软件ABAQUS对泄洪闸导墙部分的抗滑稳定及静动应力分布规律进行了计算研究并指出，在建立三维模型时，对各部件之间的接触参数进行合理设置才能得到更准确合理的计算结果. 樊志远等［6］以闸基底面与地基间接触面为滑动面，建立了沉井基础水闸的三维有限元计算分析模型，然后根据闸基底单元应力结果对闸室抗滑稳定安全系数进行了计算.

为了提高水闸的稳定性，工程设计者将齿墙引入水闸底板设计，于是含齿墙的异型底板水闸得到了广泛应用. 迄今关于异型底板水闸稳定性计算的研究也有不少. 俞根新［7］从土体剪切破坏的角度出发，运用土压力理论推导出了用于计算含齿墙底板水闸的抗滑稳定安全系数的一般公式. 阮长青等［8］通过研究认为齿坎式挡土结构物的地基剪切破坏带并非闸基底面与地基间接触面区域，而是始于墙踵，穿过齿坎底端，逸出点位于墙趾外一定距离处，在结构型式上，该齿坎式挡土结构物与含齿墙底板水闸非常相似，研究结果可为含齿墙底板水闸基底区域剪切破坏带的研究提供参考. 王千等［9］运用刚体极限平衡法和有限元强度折减法分析了齿墙对水闸的抗滑作用并指出，设置齿墙后水闸的滑动破坏模式从“滑移-倾覆”混合模式转变为滑移模式，抗滑稳定性明显提高. 但目前关于异型含齿墙底板水闸整体结构稳定性的研究较少. 鉴于此，本研究选取含有异型齿墙底板的某防洪水闸工程为研究对象，借助有限元软件Midas/GTS 建立了地基与水闸结构的整体三维有限元模型，在考虑结构间摩擦行为以及结构缝对结构响应的影响的基础上，分析了整体效应下水闸底板的应力与变形情况，然后基于有限元强度折减理论研究了水闸底板的失稳破坏模式，最后分别采用有限元模拟法和传统计算方法对水闸结构的安全系数进行了计算，并对两种计算结果进行了对比分析.

1 三维有限元模型的构建与参数的选取

1.1 有限元模型的构建

以某防洪水闸工程为研究对象，该水闸工程的主体结构包括闸室、泵站、左岸、右岸，其中闸室底板设有前后齿墙，泵站底板设有中齿墙，闸室由左边联、中联、右边联三部分组成（图1），该水闸工程结构全长94.6 m.水闸结构发生滑动或者倾覆的本质是水闸结构受到各工况下不同荷载的影响时与地基土体相互作用后达到的运动状态，因为水闸的上部结构与地基土体接触较少，所以与地基土体接触紧密的水闸底板就成为研究水闸结构稳定性的重点，但考虑到整体效应以及地形地貌等具体情况，本研究将整个防洪水闸工程结构和地基视为一个整体来构建三维有限元模型，如图1（a）所示. 为了减小模型边界的选取对计算结果的影响，根据Sabnis等［10］的研究，本研究选定的模型计算范围为：水闸底板向下30 m，防洪水闸工程主体结构往上游30 m、往下游36 m，顺水流方向长86 m，防洪水闸工程主体结构往左、右岸各50 m，垂直水流方向长194.6 m.采用Midas/GTS 软件中的混合自动网格对三维有限元模型进行网格划分，最终将三维有限元模型的整体网格划分为597 050个单元，共477 132个节点，其中闸室与泵站共包含254 385个单元，152 943个节点. 取闸室中联底板中心点为坐标原点，x轴正向为顺水流方向，y轴正向为右岸到左岸方向，z轴正向竖直向上. 模型底部采用固定约束，x、y方向两侧边界为法向约束，模型顶部自由.

考虑到工程跨度以及《水闸设计规范》（SL 265—2016）［1］中对于结构长度和面积的要求，同时为了防止水闸结构出现裂缝，在设计工程时对水闸结构进行了分缝处理，待施工完成后对分缝进行止水设置与泡沫材料填充，由于此部分并未参与力的传递，故对分缝位置进行留缝处理，图1（b）为水闸结构分缝位置示意图. 在一定的受力条件下，水闸与地基之间的接触面上会出现错动滑移甚至脱离的情况，需引入接触单元来模拟其接触状态. 本研究中，采用遵循库伦摩擦法则的接触单元模型来模拟水闸底板与地基土体之间的接触. 本次计算中，工程资料地基承载力特征值为900 kPa，根据《水闸设计规范》（SL 265—2016）［1］中的要求以及水闸底板所在地质情况，将水闸底板与地基土体之间的摩擦系数取值为0.40.

图1 水闸与地基整体三维有限元模型示意图Fig.1 Schematic diagram of the overall three-dimensional finite element model of sluice and foundation

1.2 本构模型及参数选取

根据工程地勘资料中的地层属性特点，将水闸下地基土层划分为4层，自上而下编号，如图1（a）所示，各层地基土体的物理力学参数见表1，其中水闸底板位于第4层地基中. 计算时，参考以往类似工程建立模型的经验［11-13］，闸室和泵站等结构混凝土材料采用线弹性模型，地基土体材料采用基于Drucker-Prager 屈服准则［14］的理想弹塑性模型，闸室与泵站结构材料的物理力学参数见表2.

表1 各层地基土体的物理力学参数Tab.1 Physical and mechanical parameters of foundation soil of each layer

表2 闸室与泵站结构材料的物理力学参数Tab.2 Physical and mechanical parameters of structural materials of lock chamber and pump station

1.3 计算荷载及工况

为了使计算结果能够准确反映实际工程情况，根据《水闸设计规范》（SL 265—2016）［1］中的要求，对水闸结构的6种工况（见表3）进行了计算分析，各工况荷载情况如表4所示. 其中静水压力、浪压力根据不同工况水位情况，在模型临水部分施加法向面压力；采用全截面直线分布法计算得到扬压力后将其施加在底板；假定闸室闸墩顶高程以上的工程结构的自重荷载通过支撑柱传递到闸墩以及泵站顶部，在对应的墩顶柱底连接面施加等效均布力进行模拟，同时作用在工程上部结构的风压力等效为施加在墩顶柱底连接面的剪力与力矩；地震荷载通过拟静力法进行计算.

表3 各工况水位Tab.3 Water level of each working condition

表4 各工况荷载情况Tab.4 Load situation of each working condition

2 水闸底板的变形与应力分析

2.1 水闸底板的变形分析

通过有限元模拟计算可得防洪水闸工程在各工况条件下的变形情况，通过分析可知该防洪水闸工程结构在水平方向上的位移较小，主要为竖直方向的沉降位移. 图2 为完建工况下水闸底板的竖向位移等值线云图. 以完建工况下沉降完毕位置为位移起点，通过计算可得到其他5 种工况下水闸底板的竖向位移增量，如图3 所示. 图2 和图3 中正负号代表位移方向，正号表示位移竖直向上，负号表示位移竖直向下，以位移值的绝对值大小判断位移大小.

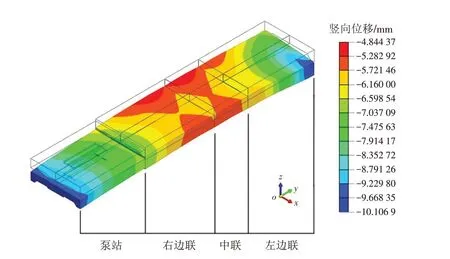
图2 完建工况下水闸底板的竖向位移等值线云图Fig.2 Contour nephogram of vertical displacement of sluice floor under completed construction condition

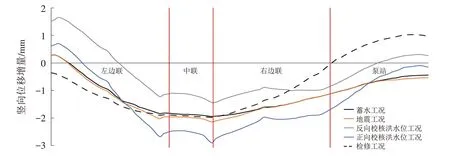
图3 各工况下水闸底板的竖向位移增量曲线图Fig.3 Vertical displacement increment curve of sluice floor under various working conditions

从图2可知，完建工况条件下，由于两侧闸墩以及上部荷载共同作用，水闸底板与闸墩连接处的竖向变形均大于水闸底板中部，水闸底板呈现出明显的中部高、两侧低的“拱形”变形特征. 因为工程左岸侧向土压力与上部闸墩的共同作用，水闸底板左边联处的竖向位移最大，其位移值为10.106 9 mm，方向竖直向下. 从图3可以看出，各工况下水闸底板竖向位移增量相对较小. 综上可知，该防洪水闸工程的最大位移和最大位移增量均符合水闸结构施工的变化规律，满足工程规范要求.

2.2 水闸底板的应力分析

图4为完建工况条件下水闸底板的应力云图，可以看出，水闸底板各部分的应力分布是不均匀的.

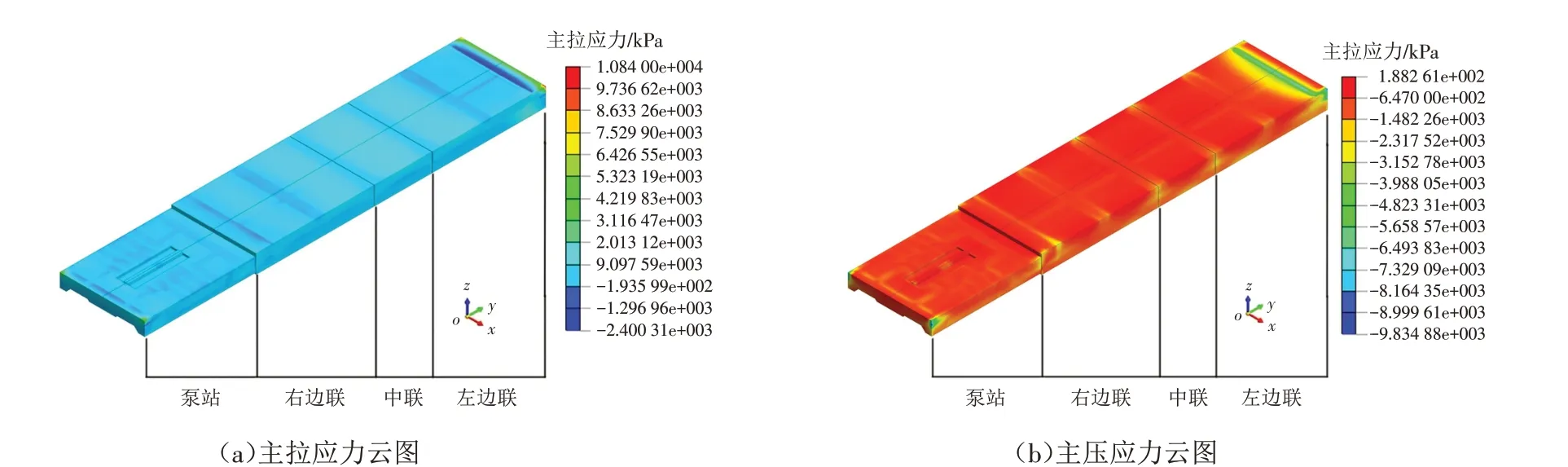
图4 完建工况下水闸底板的应力云图Fig.4 Stress nephogram of sluice floor under completed construction condition

通过分析应力计算结果可知，完建工况条件下水闸底板的主拉应力与主压应力均不超过强度标准值要求，且其他5 种工况条件下水闸底板的应力变化也不大，整体上都在规范要求的范围内，均满足规范要求.受工程两岸布置影响，左岸侧闸室底板和右岸侧泵站底板以及两者对应的边闸墩连接处的应力均较大，所以配筋过程中在配置构造钢筋后还需验算应力较大部位是否需配置一定量的抗拉钢筋.

3 水闸结构失稳破坏模式及稳定性分析

3.1 失稳破坏模式分析

准确计算水闸结构安全系数的关键是要确定水闸结构的滑动破坏面与倾覆转动轴所在的位置. 与计算稳定性时需预先指定破坏面的极限平衡法不同的是，有限元强度折减法［15-16］的基本原理是在数值计算过程中对材料强度进行折减，该方法可以在地基情况与结构受力复杂的条件下确定结构与地基整体的失稳破坏面. 本研究所用的防洪水闸工程，在闸室底板设有前后齿墙，泵站底板还另设有中齿墙. 因此，本研究中，利用Midas/GTS 有限元软件，基于有限元强度折减理论对水闸底板的实际失稳破坏面进行定位. 通过模拟计算得到的两种底板的失稳破坏面如图5（a）和图5（b）所示，图5（c）为常见无齿墙底板的失稳破坏面示意图.

从图5 可以看出，在设置齿墙之后，水闸结构的失稳破坏面并非底板与地基间的直接接触面，而是从齿墙底面出发向着底板侧凸起发展的剪切破坏带（地基土体中黄绿色部分）所构成的圆弧面，失稳破坏面以上的地基土体与水闸底板可以被视为一个整体一起运动. 分析其原因为：齿墙对于相邻两齿墙间地基土体的推动、下压和下部土体本身的黏聚力的共同作用使得水闸结构的失稳形式并不是严格地沿水平面滑移，中齿墙的作用可以认为是将底板分成两块相对跨度较小的前后齿墙底板. 根据计算结果可以确定，该防洪水闸工程中的闸室底板和泵站底板的失稳破坏面均为上述圆弧面和齿墙底-地基交界面，倾覆转动轴为倾向侧齿墙外沿.

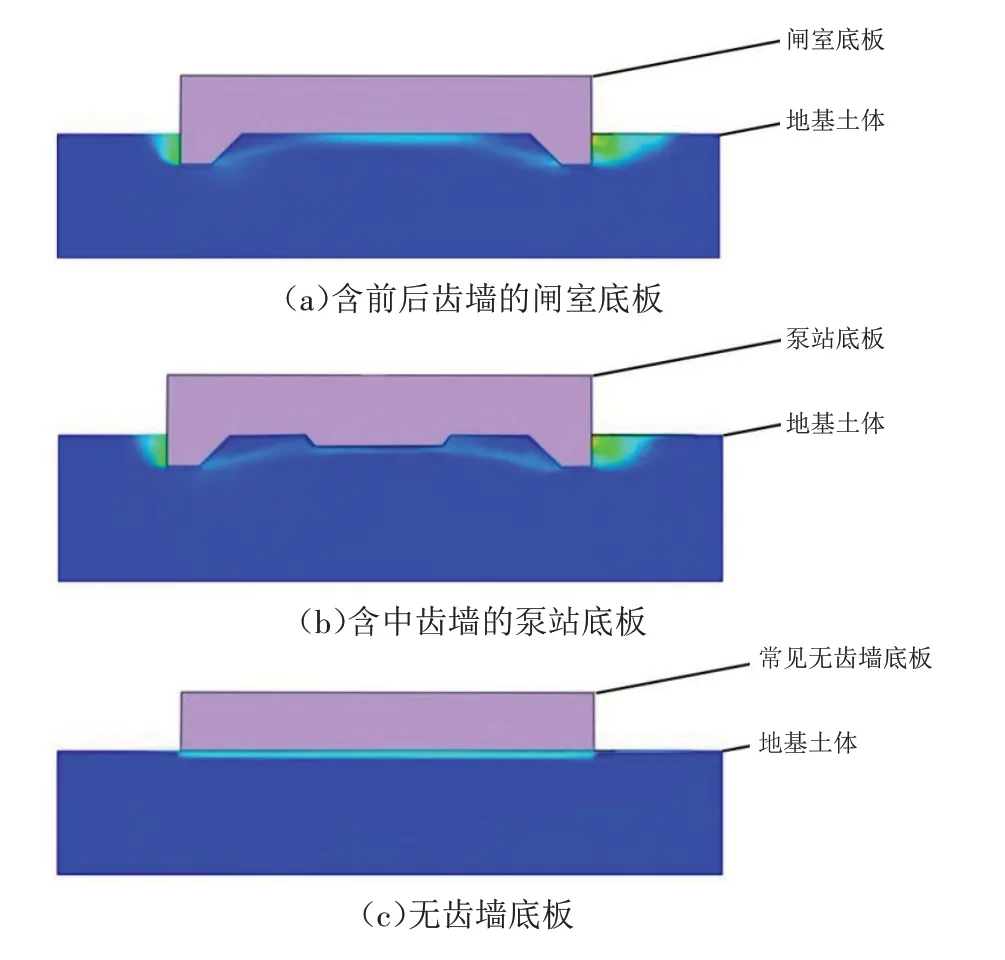
图5 三种底板的失稳破坏面示意图Fig.5 Schematic diagrams of the instability failure surfaces of three kinds of sluice floors

3.2 安全系数计算方法

安全系数是度量工程结构稳定性的一种基本指标［17-18］，不同工程结构的安全系数计算方法也有所不同［19-20］. 根据上述分析结果可知，当该防洪水闸工程的闸室底板和泵站底板出现滑动趋势时，抑制滑动的力分为以下几部分：失稳破坏面上下两侧的地基土体间的摩擦力、齿墙底面与地基土体间摩擦力、水闸两岸侧边墙与两岸地基土体的接触摩擦力、水闸底板后墙与地基土体间的黏结力、水闸底板前地基土体的抗力. 综合考虑上述滑动过程以及力的分布情况后，将水闸结构的抗滑稳定安全系数Fs的表达式设定如下：

式中：φ为地基土体内摩擦角；Fc为相邻两齿墙间的剪切破坏带圆弧面上的地基土体单元竖向力总和，在软件中通过局部内力部件提取并通过应力积分求得；f为地基土体与水闸底板间摩擦系数，通过现场摩擦实验测得；σs为水闸结构与地基土体接触面上的正应力，包括水闸齿墙底部与地基土体接触面上的正应力和水闸两岸侧边墙与两岸地基土体接触面上的正应力；As为各个力对应结构部分与地基土体接触面的面积；σ′为水闸底板齿墙与地基土体接触面上的正应力，A′为水闸底板齿墙与地基土体接触面的面积；∑H为水平外力总和.

在分析水闸抗倾覆稳定性时，以水闸底板底部前沿为倾覆轴. 当水闸整体出现倾倒趋势时，抑制倾覆的力矩包括：水闸及上部结构整体自重以及水闸底板齿墙与地基土体接触面支撑力所产生的力矩. 导致倾覆的力矩包括：水闸所受外力产生的力矩以及水闸底板齿墙与地基土体接触面压力所产生的力矩. 综合考虑上述倾覆过程以及力矩的分布情况后，将水闸结构的抗倾覆稳定安全系数Fm的表达式设定如下：

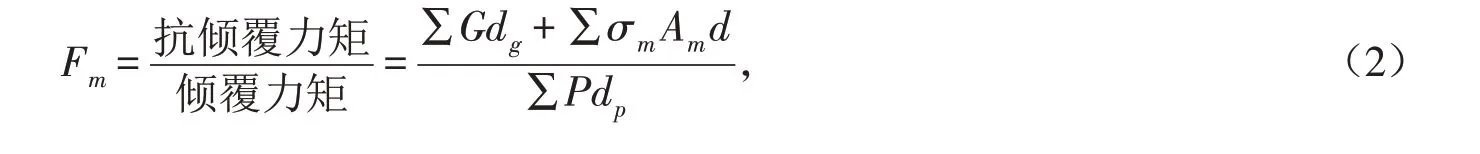
式中：G为水闸及上部整体结构（其中包含滑动面以上地基土体）的重力；σm为水闸底板与地基土体接触面上的正应力；Am为水闸底板与地基土体接触面面积；P为作用于水闸结构上的各组外力；dg、d、dp分别为各力与倾覆轴的距离.

3.3 安全系数计算结果

由于完建工况中没有对水闸结构产生水平方向上影响的外荷载，所以完建工况条件下水闸结构必然稳定，故采用有限元模拟法，结合公式（1）和公式（2），对其余5种工况下水闸各结构的安全系数进行计算，同时与按照传统计算方法计算得到的安全系数进行对比，结果如表5和表6所示，表中规范允许值为《水闸设计规范》（SL 265—2016）中要求的结构必须达到的安全系数最小值.

表5 采用不同方法计算得到的不同工况下水闸各结构的抗滑稳定安全系数Tab.5 The anti-sliding stability safety factors of each sluice structure under different working conditions calculated by different methods

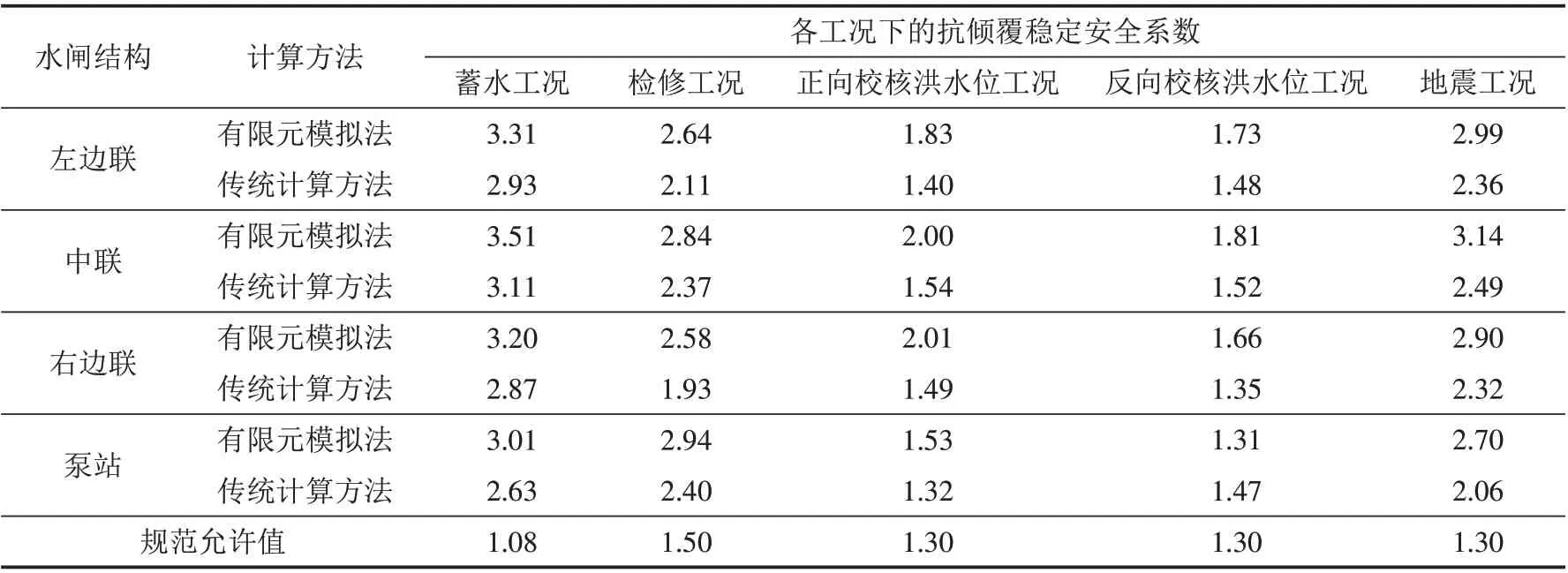
表6 采用不同方法计算得到的不同工况下水闸各结构的抗倾覆稳定安全系数Tab.6 The anti-overturning stability safety factors of each sluice structure under different working conditions calculated by different methods

从表5和表6可以看出，通过有限元模拟法计算得到的各工况下水闸各结构的抗滑稳定安全系数和抗倾覆稳定安全系数都大于规范允许值，均满足结构稳定性要求；利用传统计算方法计算得到的各工况下水闸各结构的抗倾覆稳定安全系数均满足规范要求，但有部分抗滑稳定安全系数不满足规范要求. 通过有限元模拟法计算得到的安全系数大部分都大于采用传统计算方法得到的安全系数，说明传统计算方法的计算结果更偏安全保守. 在检修工况和正向校核洪水位工况下通过传统计算方法计算得到的右边联抗滑稳定安全系数大于通过有限元模拟法计算得到的结果，在反向校核洪水位工况下通过传统计算方法计算得到的泵站抗倾覆稳定安全系数大于通过有限元模拟法计算得到的结果，分析原因可能是有限元模拟法考虑了施加在左右岸边墙的土压力的外部作用以及相邻结构物的整体结构的内部作用，这也说明了整体效应对水闸工程的稳定性产生了负面影响，在工程设计时，需要对这些部位进行复核检查，甚至进行加强. 在设计阶段计算水闸工程稳定性时，建议采用三维有限元模拟法，因为有限元模拟法能将水闸结构与地基间的相互作用考虑进去，计算出的结果更符合工程实际情况，且该方法能在补充修正传统计算方法和定位类似的工程隐患位置方面发挥作用.

4 结论

通过三维有限元软件Midas/GTS 建立了某防洪水闸工程结构与地基的三维有限元模型，分析了多种工况下水闸底板的变形与应力情况，在考虑结构间摩擦行为以及结构缝对结构响应的影响的基础上，运用有限元强度折减理论研究了异型含齿墙水闸底板的失稳破坏模式，并采用有限元模拟法和传统计算方法计算了水闸结构的安全系数，得到以下结论：

1）构建的三维有限元模型可以准确地模拟水闸的结构缝以及水闸结构与地基间的相互作用，计算得到的水闸底板的位移变化和应力变化均满足工程规范要求.

2）采用三维有限元软件，通过有限元强度折减法，能够准确找到异型含齿墙水闸底板的失稳破坏面，确认其失稳破坏模式，根据破坏面所在位置提取对应的有限元计算结果，再结合安全系数计算公式可以获得水闸结构的安全系数，进而判断其稳定性. 与传统计算方法相比，三维有限元模拟法计算得到的安全系数总体偏大，可以作为补充修正传统计算方法的有效途径.

3）在设计阶段计算水闸工程稳定性时，建议采用三维有限元模拟法，因为该方法可将水闸结构与地基间的相互作用考虑进去，计算出的结果更符合工程实际情况.