颗粒浓度对离心泵性能及磨损影响的研究

黄 凯，刘 栋，尤保健，倪子建，宋 涛

（1.江苏大学 能源与动力工程学院，江苏镇江 212013；2上海凯泉泵业（集团）有限公司，上海 201804）

0 引言

离心泵广泛应用于矿山、化工、冶金、电力等领域的固液两相流输送。固体颗粒不仅影响离心泵的水力性能，还容易造成过流部件的磨损，导致泵的使用寿命缩短［1-6］，因此，提高水力性能和抗磨损性能是设计固液两相流泵需要考虑的主要问题。

随着两相流数值模拟方法的发展，许多学者采用数值计算研究了固体颗粒对离心泵性能的影响规律。刘厚林等［7］基于Mixture模型研究了双流道泵内固液两相流动，结果表明颗粒浓度的变化对泵内静压和外特性等有较大的影响，而粒径的影响较小。ZHANG等［8］利用Mixture模型研究了离心泵固液两相流动，结果表明粒径和浓度对离心泵的水力性能有很大的影响。王献等［9］采用DPM模型研究了离心泵输送粗颗粒时的两相流动，揭示了颗粒直径和浓度对颗粒的过泵时间和泵外特性的影响规律。

在离心泵过流部件磨损特性的研究方面，PENG等［10］采用欧拉模型模拟了离心泵固液两相流动，讨论了颗粒浓度对叶轮以及蜗壳内磨损的影响规律。赵伟国等［11］基于DPM模型和Finnie磨损模型计算了离心泵内部的固液两相流动，结果表明磨损部位主要集中在叶片的进口边、叶片背面和叶片工作面靠近出口的位置。邵文博等［12］基于CFD-DEM方法对多级混流泵的磨损进行模拟计算，发现叶片磨损严重的地方在头部和尾部，颗粒的球形度减小导致磨损量急剧增大，颗粒的浓度和形状对叶片磨损位置影响小。

综上所述，研究人员基于不同模拟方法对离心泵的性能和过流部件的磨损进行研究，但在颗粒浓度对离心泵的水力性能及叶轮磨损影响的研究方面还不够深入。本文采用CFD-DEM耦合的方法计算离心泵内固液两相流动，定量分析颗粒浓度对泵内流场以及叶轮磨损的影响规律，相关结论可为固液两相泵的优化设计提供参考。

1 计算模型及方法

1.1 离散元方法

在Lagrange坐标系中，每一个颗粒的受力在每个时间步中都会更新，并通过求解牛顿运动方程获得颗粒的新位置和速度［13-14］。固相颗粒的牛顿运动方程如下：

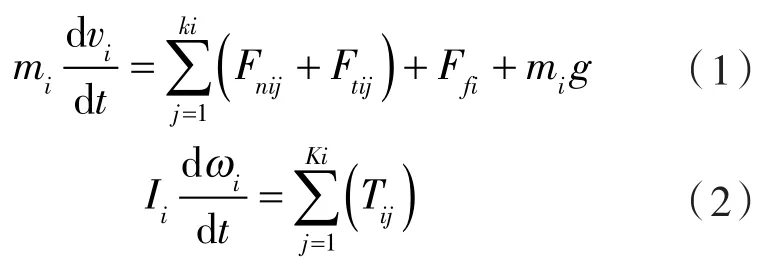
式中 mi，vi——颗粒i的质量和速度；

g ——重力加速度；

Fnij——颗粒i和j之间的法向接触力；

Ftij——颗粒i和j之间的切向接触力；

Ii——颗粒i的转动惯量；

ωi——颗粒i的角速度；

Ffi——液相对颗粒i的作用力；

Ti——颗粒i的滚动摩擦力矩。

选用Hertz-Mindlin无滑动接触模型，该模型是在Mindlin等［15］所取得的研究成果基础上建立的。

设颗粒i和颗粒j两球形颗粒发生弹性接触，法向重叠量α的计算公式为：

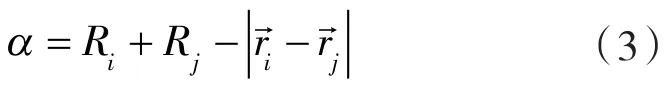
颗粒间的接触面为圆形，接触半径a为：

式中 R*——等效颗粒半径。

R*可由下式求出：

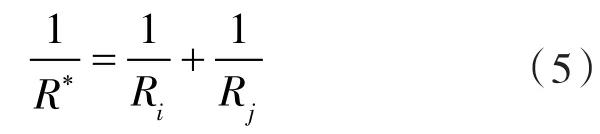
颗粒间法向力Fn可由下式求得：

式中 E*——等效杨氏模量；

Ei，Ej——颗粒i和颗粒j的杨氏模量；

μi，μj——颗粒 i和颗粒 j的泊松比。

式中 e ——恢复系数；

m*——等效质量；

Sn——法向刚度，

颗粒间的切向力Ft可由下式求出：

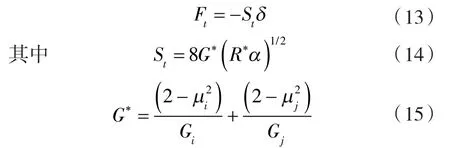
式中 St——切向刚度；

δ ——切向重叠量；

G*——等效剪切模量；

Gi，Gj——颗粒 i和 j的剪切模量。

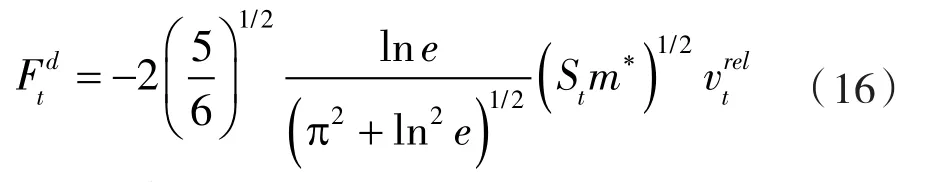
1.2 磨损模型

根据文献［16］中描述的颗粒与叶片的接触方式，将颗粒对过流部件的磨损分为两种形式：碰撞磨损和摩擦磨损。

1.2.1 碰撞磨损

离心泵过流部件的碰撞磨损是指固体颗粒直接撞击壁面导致的磨损，本文采用Oka模型［17］，表达式为：

式中 Af——壁面面积；

er——由任意角度冲击造成的磨损；

e90——冲击角为90°造成的磨损；

g（α）——冲击角函数；

α ——冲击角度；

Hv——维氏硬度；

vp——颗粒速度；

Dp——颗粒直径；

vref——参考颗粒的速度；

Dref——参考颗粒的直径；

K，a，b，k1，k2，k3，n1，n2——常数，由颗粒和壁面的物性决定。

1.2.2 摩擦磨损

摩擦磨损指颗粒沿过流部件表面作切向摩擦产生的磨损。本文选用Archard模型［18］计算该类型的磨损，表达式为：

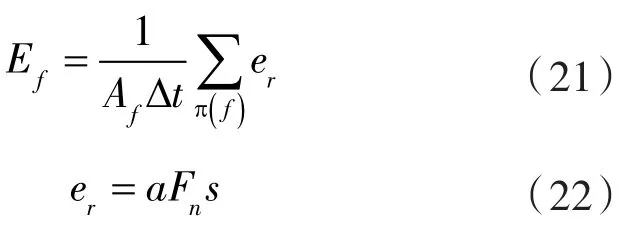
式中 Af——壁面面积；

Δt ——时间步；

er——磨损体积；

a —— 磨损系数，数值由颗粒与壁面的物性决定；

Fn——法向力；

s ——滑动距离。

1.3 磨损模型的验证

为了研究磨损模型的计算准确性，本文将叶轮简化为弯管，只考虑流动受曲率的影响［19-22］。模拟不同浓度时弯管内部的固液两相流动，并将计算结果与文献［23］进行对比分析。

1.3.1 计算模型

计算模型包括：入口延伸段、出口延伸段以及试验段，弯管的二维模型如图1所示。

图1 弯管的二维模型Fig.1 The 2D model of elbow

1.3.2 模拟设置

液相为清水，固相为3 mm的二氧化硅球形颗粒；壁面材料为铝。进口边界条件设置：液相和颗粒的速度为11.77 m/s，颗粒浓度为1%～15%；模拟时间为0.1 s，时间步长为1×10-5s，颗粒与壁面材料的参数见表1。

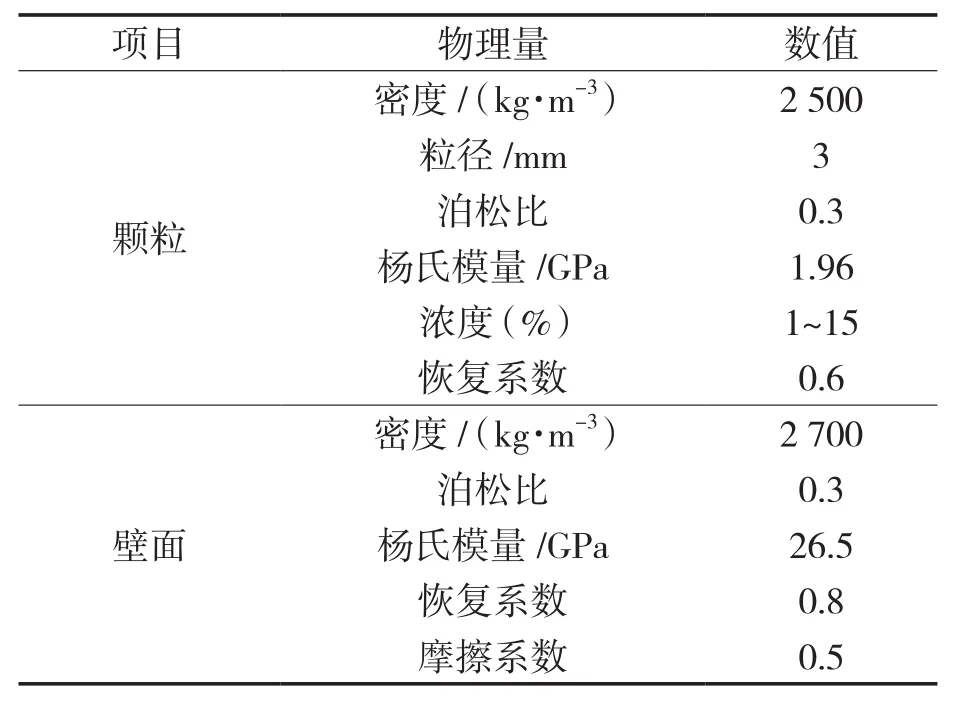
表1 颗粒和壁面（铝）的材料参数Tab.1 Material parameters of particle and wall（aluminum）

1.3.3 结果分析

图2示出颗粒浓度Cv=10%的液相速度场和颗粒分布。图2（a）示出本文计算的结果，图2（b）示出文献［23］给出的结果。结果表明，液相速度在试验段进口的内侧达到较大值，在试验段出口处，外侧附近的液相速度较大。由于试验段内的流动受弯管曲率的影响，固体颗粒在离心力作用下，多聚集在试验段的外侧壁面附近，只有刚进入试验段和离开试验段时内侧壁面附近会出现少量颗粒。

图2 流场速度和颗粒分布Fig.2 Distribution of flow field velocity and particles

在图3中，磨损比定义为壁面磨损量与Cv=1%时壁面磨损量之比，磨损量定义为模拟计算时间内弯管内壁面由于磨损而减少的质量。随着颗粒浓度从1%增加至8%，磨损比急剧增大；浓度继续增加至15%，磨损比的变化趋于平缓。本文模拟的结果与文献［23］的结果吻合较好，磨损比计算的最大误差为3.6%，这表明本文采用的模拟方法和磨损模型在描述固液两相流动和计算壁面磨损时具有较高精度。

图3 不同颗粒浓度下的磨损结果对比Fig.3 Comparison of the erosion results at different particle concentrations

2 离心泵的模拟验证

2.1 模型和网格

模型选用比转速ns=83的离心泵。设计参数：扬程H=8 m，流量Q=20 m3/h，转速n=1 450 r/min，主要参数见表2。

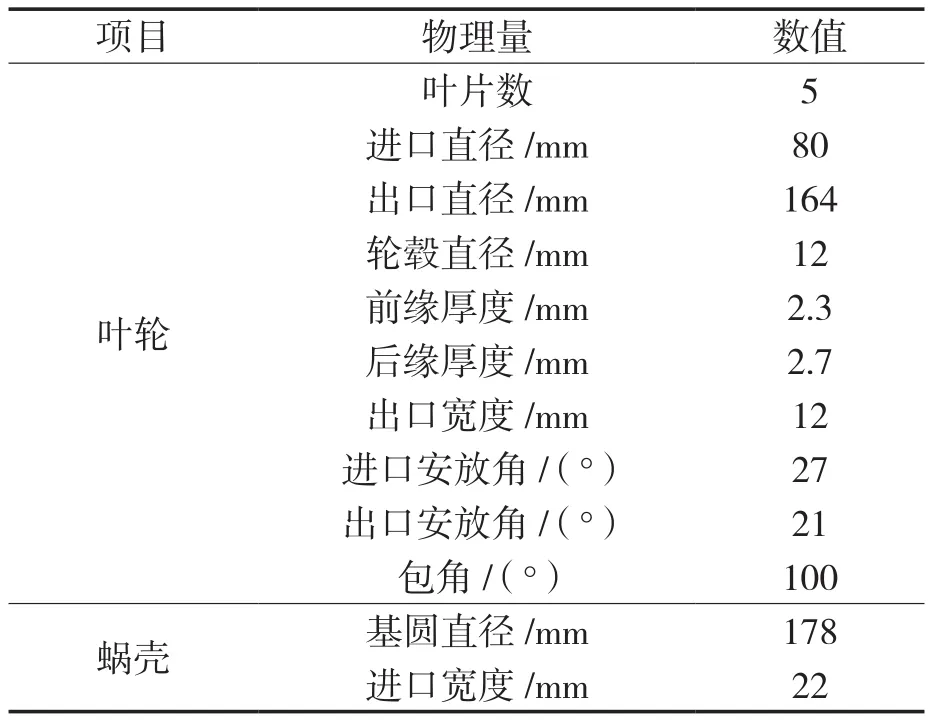
表2 模型泵的主要参数Tab.2 Main parameters of the model pump

模型泵的计算域包括叶轮、蜗壳、进口延伸段和出口延伸段。图4示出模型的网格划分，将计算域划分为5种不同数量的网格，进行网格无关性分析，如图5所示。当网格数为479 881和638 419时，扬程和效率的计算误差分别为0.09%和0.06%，考虑到计算效率，选取叶轮和蜗壳网格数为479 881。

图4 计算模型的网格Fig.4 Mesh of computational model

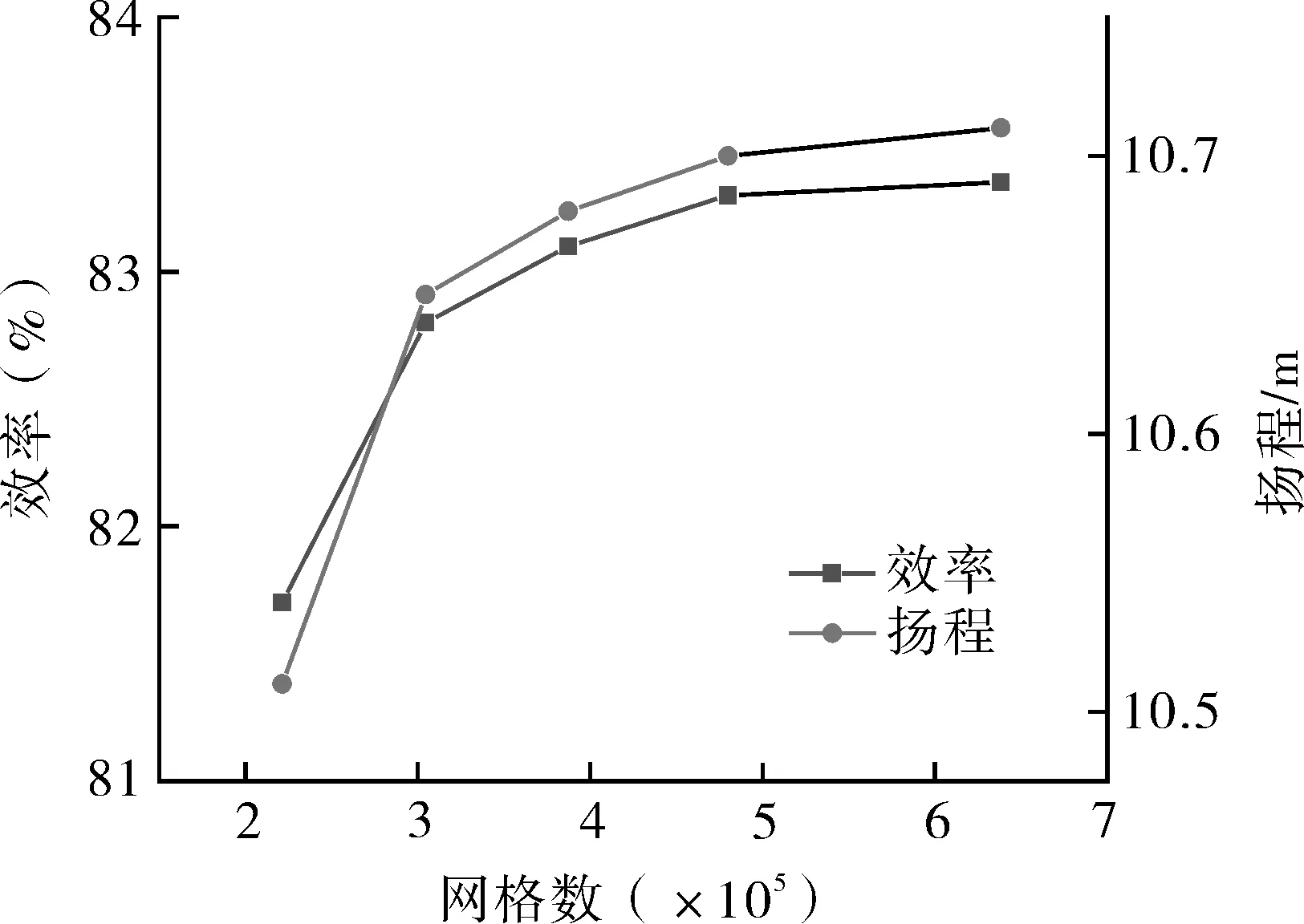
图5 网格无关性分析Fig.5 Grid independence analysis

2.2 模拟设置

设置模拟计算时间步长为1.494×10-4s，即叶轮每旋转1°计算一次，总计算时间为0.206 9 s，即叶轮旋转5圈。固相为2.5 mm的二氧化硅球形颗粒，壁面材料为碳钢，具体材料参数见表3。

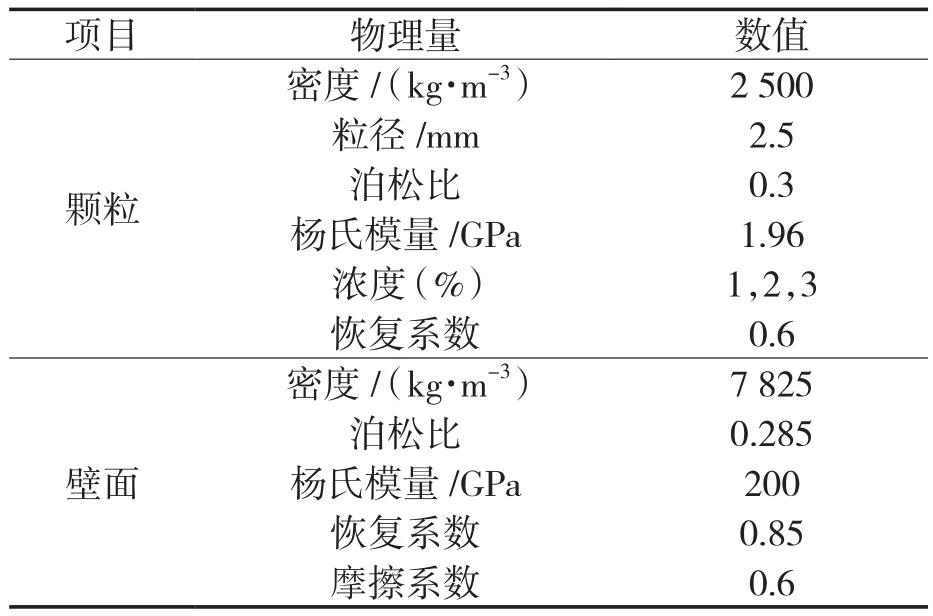
表3 颗粒和壁面（碳钢）的材料参数Tab.3 Material parameters of particle and wall（carbon steel）

2.3 外特性计算结果及验证

为验证数值模拟结果的可靠性，在闭式实验台上完成了离心泵输送清水和固液两相流（Cv=1%）的外特性实验。计算和试验测试结果如图6所示，当离心泵输送固液两相流时，性能显著下降，模拟和试验结果的变化趋势一致，效率和扬程计算的最大误差分别为3.9%和3.5%，这表明应用CFDDEM耦合的方法研究离心泵内固液两相流流动具有较高精度。

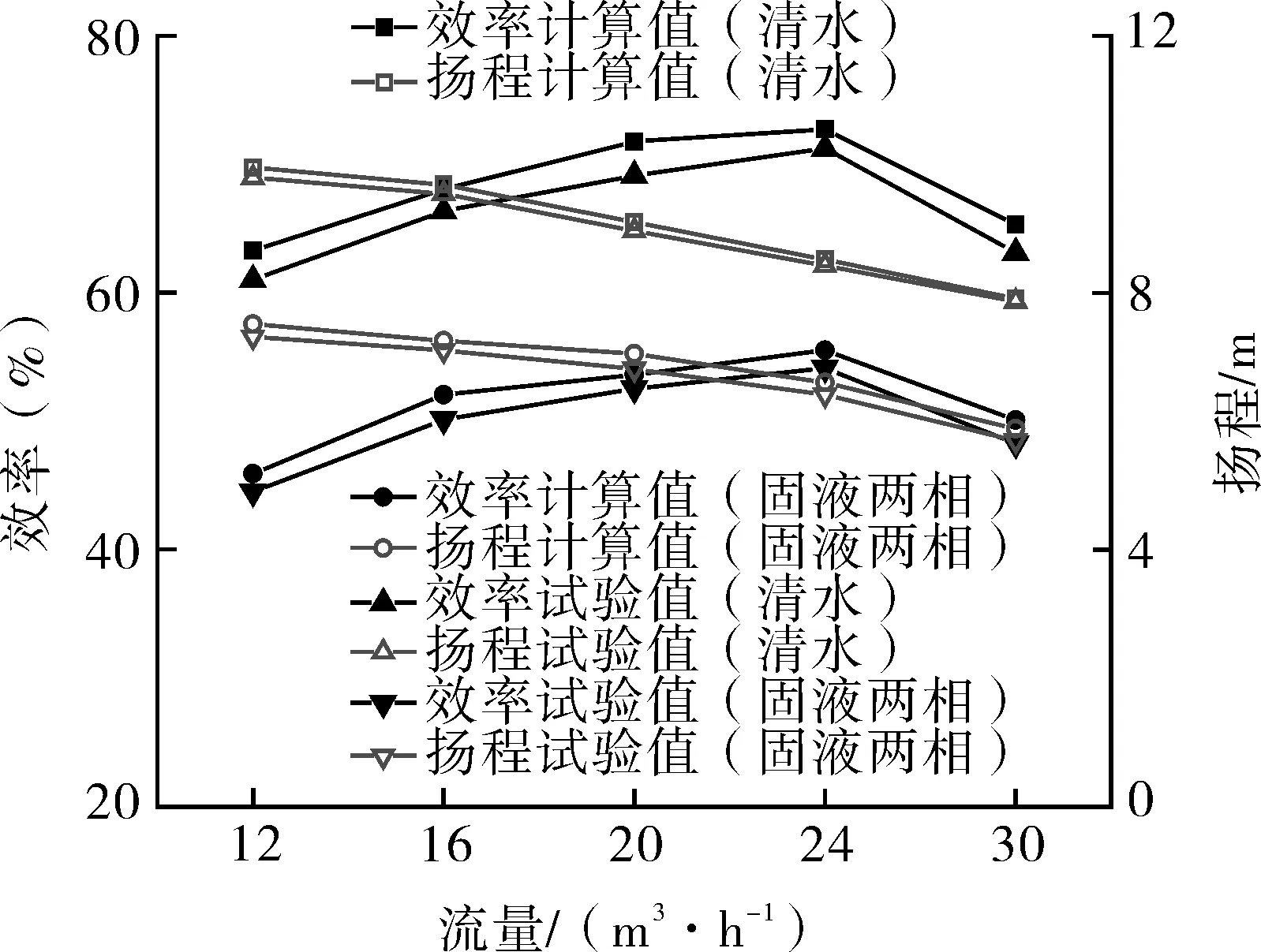
图6 试验与数值计算结果对比Fig.6 Comparison of experimental and numerical calculation results

3 模拟结果与分析

表4为不同颗粒浓度下，模型泵外特性和叶轮磨损率的计算结果。表中的叶片磨损率占比定义为叶片磨损率与叶轮磨损率之比。计算结果表明，当颗粒浓度为1%时，模型泵的扬程和效率相比于清水工况均有较大幅度的降低，并且随着颗粒浓度的增大，扬程和效率逐渐减小，磨损率逐渐增大。通过对过流部件磨损的监测，叶轮的磨损率占总磨损率的95%，叶片的磨损率占比大于50%。由此可见，叶片是该离心泵的主要磨损部件。

表4 颗粒浓度对性能和磨损的影响Tab.4 Effect of particle concentration on pump performance and erosion

为了提高叶轮的抗磨损性能，必须深入研究叶片的磨损规律。图7示出了不同颗粒浓度下叶片的磨损率分布。

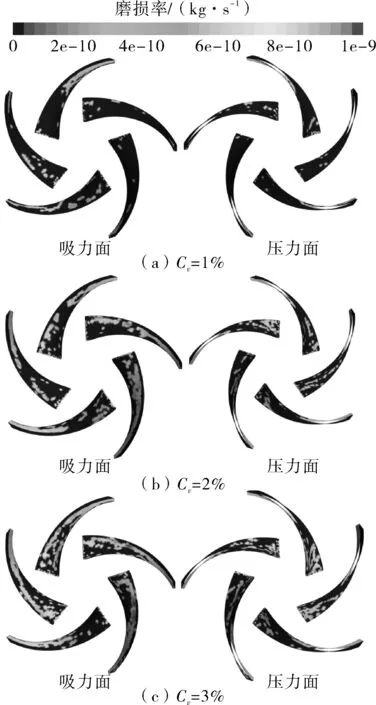
图7 不同浓度下叶片的磨损率分布Fig.7 Erosion rate distribution of blades at different concentrations

由图7可知，吸力面比压力面的磨损更严重；当浓度为1%时，叶片进口附近发生磨损，磨损区域的形状多为点状，随着浓度的增大，点状磨损区域增多且逐渐连成片状。吸力面的磨损主要出现在中间至叶片出口边，中间位置的磨损最严重。当浓度从1%增加到3%时，叶片最大磨损率分别为 8.12×10-10，8.68×10-10，9.96×10-10kg/s，该数值对应的区域磨损最严重。由此可知，叶片磨损最严重的浓度为3%。这是由于随着颗粒浓度增大，颗粒数目增多，颗粒对壁面的接触概率增大，加剧壁面的磨损。

文献［23］通过监测样本颗粒的平均速度来反映颗粒的运动状态，并通过颗粒平均速度的变化来分析磨损产生的原因。本文在模型泵进口随机选取100个颗粒，计算样本颗粒的平均速度，如图8所示。不同浓度下颗粒的平均速度变化趋势相似，颗粒在泵内的运动主要经过3个阶段：加速阶段、减速阶段以及波动阶段。在加速阶段过程中，叶片对颗粒做功，颗粒的运动速度呈现逐渐上升的趋势，由此可以确定颗粒在叶轮内的运动时间t。随着颗粒浓度从1%增加到3%，t分别为0.081，0.085，0.096 s，颗粒在叶轮中运动时间最长的情况为Cv=3%，这导致颗粒与叶轮接触的概率增大，加剧了该工况下的磨损。

图8 颗粒的平均速度Fig.8 Average velocity of particles

颗粒对壁面的冲击和摩擦产生的接触力和接触次数决定了壁面磨损的程度。由图8的结论可知，颗粒浓度增大后，颗粒在叶轮内运动的时间变长，导致接触次数增多，不同浓度的接触次数分别为1 412，4 484和7 141。图9示出不同浓度下颗粒与壁面的接触力沿叶轮半径方向的分布，随着颗粒浓度增大，接触力逐渐增大，接触力较大的区域从半径45～58 mm扩大到45～69 mm，该区域对应叶轮磨损最严重的部分。

图9 颗粒与壁面间的接触力沿叶轮半径方向的分布Fig.9 Distribution of contact force between particles and wall along impeller radius

在不同颗粒浓度时，叶片磨损严重处的接触力如图10所示。接触力几乎垂直于壁面，颗粒与壁面接触时的冲击角接近90°。由磨损模型可知，磨损率的大小与冲击角相关，冲击角越接近90°，磨损越严重，与图7中磨损率较大的位置一致。

图10 不同浓度下磨损严重处的接触力Fig.10 Contact force of serious erosion position at different particle concentrations

4 结论

（1）固相颗粒的存在对离心泵的水力性能影响很大。随着浓度增加，扬程和效率逐渐减小，叶轮磨损率、磨损区域、接触力和接触次数都逐渐增大。

（2）颗粒在泵内的运动可分为3个阶段：加速阶段，减速阶段和波动阶段，Cv=3%时颗粒在叶轮内加速运动的时间最长。

（3）Cv=3%时，颗粒与叶片的接触力较大，接触次数最多；在叶片吸力面磨损最严重位置，颗粒对壁面的冲击角接近90°。