相变蓄热材料对蓄热水箱分层特性的影响
仵 凡,张 华,王子龙,秦延斌
(上海理工大学 能源与动力工程学院,上海 200093)
0 引言
在太阳能利用过程中,其中关键技术之一是以水为载体的储热水箱的设计[1-5]。储热水箱作为太阳能集热系统、电加热热水系统以及热泵热水系统中的关键性设备,然而,由于水的单位质量蓄热能较小,且蓄热过程中温度变化比较大,导致太阳能利用效率较低。为了提高太阳能利用率,将相变材料(Phase Change Materials,PCM)引入太阳能储能系统,利用PCM在相变过程中温度变化小,储热密度大且价格低廉等特点,实现对热能进行高效储存和释放[6],并且在一定程度上克服了太阳能利用中的间歇性和不稳定性。
早在20世纪40年代,TELKS等[7]对相变材料进行了研究。RAMANA等[8]分析了相变蓄热材料对太阳能热水系统性能的影响机理,通过实验和模拟表明相变储热材料能有效地改善冷热水之间的热分层,同时提出进水流速是影响水箱内部热分层的关键因素。ALLOUCHE等[9]建立了一个以石蜡为原料的相变储热罐的数学模型,以模拟和试验研究储热罐中石蜡的热特性,结果表明,理论值和试验值的偏差随流体流速的增加而增加,其最大偏差为275.55 K。NAVARRO等[10]研究提出将PCM与高密度聚乙烯球相结合,加入家用热水罐中的方法,试验结果表明,PCM球在实际应用之前,必须进行热循环和清洁,以稳定PCM球内相变蓄热材料的含量。
本文在上述研究基础上,选用中低温相变材料三水合醋酸钠作为蓄热材料,设计了一种立式相变蓄热水箱,研究在不同进口流量和相变材料放置在水箱中的不同位置对相变蓄热水箱热特性的影响。
1 试验系统和仪器
1.1 试验系统
试验系统如图1所示,本试验系统主要有:蓄热水箱、恒温浴、恒温水箱、回收水箱、变频泵、循环泵、流量计、节流阀等,选用蓄热球外壁为PVC材料,厚度为2 mm,外径为40 mm的三水合醋酸钠小球为相变蓄热单元。系统整体使用保温棉覆盖,水箱内加装1.5 kW的加热设备,并通过循环泵,使水箱内部水温均匀分布。蓄热水箱容积为60 L,采用下进上出的循环模式。

图1 试验系统Fig.1 Experimental setup
1.2 试验仪器
试验仪器包括OMEGA FLR1013-D流量计,Agilent 34970数据记录仪,扫描时间间隔为2 s。14根Pt100的铂电阻,均匀布置在蓄热水箱一侧,其测量精度为±(0.15+0.002|t|)。蓄热水箱中铂电阻布置位置如图2所示。
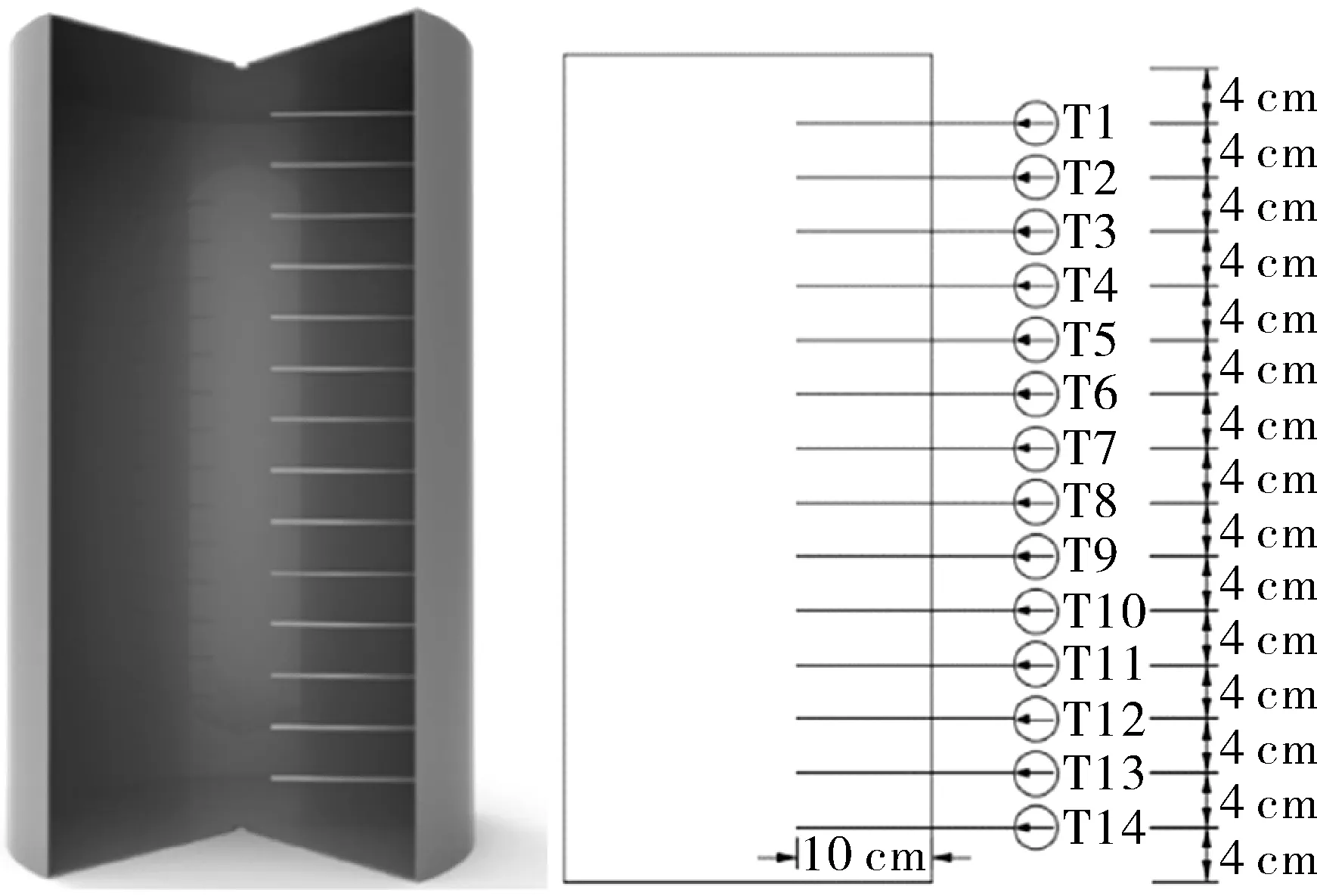
图2 水箱中铂电阻的位置Fig.2 Schematic diagram of the location of the PT100 in the tank
2 计算模型
2.1 无量纲时间
将进水时间t与当前体积流量下水箱中的水被完全置换一次的时间t0的比值定义为无量纲时间t*:

2.2 理查德森数
理查德森数Ri表示浮力和流剪切项的比值的无量纲数[11]。

式中 g ——重力加速度,m/s2;
β ——膨胀系数,1/K;
H ——水箱高度,m;
Ttop,Tbottom——水箱顶部、底部温度,K;
vs——进入水箱的平均流速,m/s,
rstratifier——水箱进水口当量半径,m。
2.3 混合数
混合数[12]用来表征某一时间点水箱内的热分层效果。其中,水箱的动量Mexp与水箱完美分层时的动量值Mstratified和水箱完美混合时水箱的动量值Mfull-mix相关。
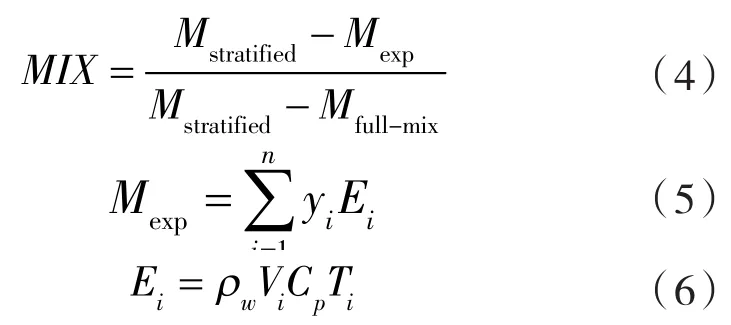
式中 yi—— 为水箱第i层重心到箱底的垂直距离,m;
Ei——水箱第i层具有的能量,J;
ρw——水的密度,kg/m3;
Vi——水箱第 i层体积,m3;
Cp——水的定压比热容,J/(kg·K);
Ti——水箱第i层的温度,K。
假设实验水箱的总能量与完美分层水箱总能量相同,并且定义 Thot=80 ℃,Tcold=10 ℃,则 Vhot和Vcold定义为:
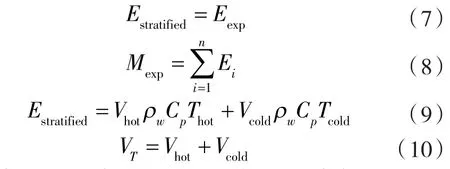
斜温层的位置ystratified由式(11)确定:


2.4 填充效率
蓄热水箱从进水的一瞬间开始到某一时间t,水箱的总能量:
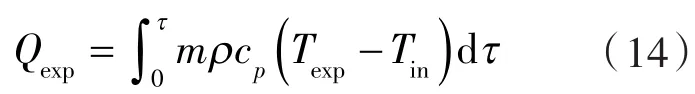
理想分层的水箱总能量:

填充效率:

3 模型的建立
3.1 物理模型
本试验水箱及相变蓄热球通过三维绘图软件Proe中建立数学模型,之后通过ANSYS软件中的ICEM,对水箱网格进行划分,在网格划分过程中采用了非结构网格,并对温度和流动变化复杂区域的网格进行了细化加密处理,划分后的网格如图3所示。

图3 水箱网格Fig.3 Grids of the water tank
3.2 控制方程
考虑到本文所建立的三维模型是通过能量方程和基于黏性不可压缩流体动量守恒运动方程来计算其热分层特性。因此,本文采取以下控制方程[13-15]。
质量方程:

动量方程:
这已然为事实证明。去年,几段展现“塑料紫菜”的视频在网上广泛传播,引发一轮“塑料紫菜”风波。据了解,造谣者王某在食用某食品公司生产的紫菜后,猜想这些紫菜是塑料做的,便指挥员工拍摄视频并上传到朋友圈。其后,王某联系被害公司索要人民币10万元,威胁如果不解决问题,就把事情闹大。还有多家食品企业称,一些集中爆发的网络谣言很有可能是竞争对手在背后捣的鬼。中国传媒大学教授王四新表示,确实有一些别有用心的竞争对手通过抹黑的方式故意散布谣言,意图牟取不当市场利益。
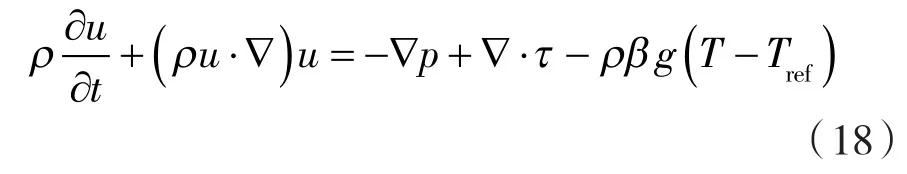
能量方程:

相变材料的相变过程采用焓法来求解,焓法模型为:

3.3 边界条件
初始条件及边界条件见表1,进口流量分别为 1,3,5,7,9 L/min。

表1 水箱的边界条件及初始条件Tab.1 Boundary conditions and initial conditions of the water tank
3.4 物性计算
由于水的物性参数[16-17]随着温度的变化而改变,而且密度随着水温的升高而升高,因此,本文对水的物性参数引入修正公式进行修正。
密度:

运动黏度系数:

3.5 计算过程
为了研究流量对水箱性能的影响,在水箱进口流量为 1,3,5,7,9 L/min 条件下,试验测量水箱温度场变化。由于流量在1 L/min时,雷诺数小于2 300,见表2,因此本文使用k-ε湍流模型计算。其迭代收敛的最终标准为k和ε的收敛残差小于10-3,连续性,动量和能量方程收敛残差小于10-6。数值求解采用有限体积法,并采用SIMPLE算法对压力方程和流动方程进行耦合。

表2 进水流量与ReTab.2 Table of inlet flow rate and Re
4 试验结果与分析
4.1 网格数量
本文采用FLUENT数值模拟软件,将水箱内部作为计算域进行了有限元差分,模型的网格数量约为260万~460万。如图4所示,描述了当进口流量为9 L/min,网格数分别为260万、360万和460万时,水箱出口温度和时间的变化关系。随着网格数量的增加,模拟结果并没有明显的提高,且随着网格数量的增加,计算时间和成本会随之上升,因此,本文选用260万个网格数模型进行计算。

图4 不同网格数下的计算结果Fig.4 The calculation results with different grid numbers
4.2 时间步长
瞬态求解的一个关键参数是时间步长,如果时间步长设置偏大,会导致步长内很难收敛;设置偏小会增加迭代的次数,增大计算时间。因此,为了更加准确设置计算时间步长,减少迭代次数。本文首先将时间步长设置为0.1,0.5,1 s,计算结果如图5所示。计算步长为0.5 s时的计算结果与0.1,1 s时的计算结果分别相差0.19%和0.17%,而计算步长为1 s时的计算结果与0.1 s时的计算结果相差0.28%。因此,本文最终选择计算步长为0.5 s。

图5 不同时间步长下的计算结果Fig.5 The calculation results with different time steps
4.3 水箱温度特性分析
当进水流量为9 L/min时,冷水在水箱的流动过程以及水箱内的温度分布如图6所示。

图6 水箱温度特性模拟结果Fig.6 The simulation results of temperature characteristics of the tank
当冷水进入水箱当中时,冷水首先和位于水箱底部的热水相混合,因此水箱底部的铂电阻温度最先下降,而后随着放水过程的进行,在重力的作用下,密度大的冷水会向水箱底部流动,而由于浮升力的作用,热水则会流向水箱顶部,从而形成水箱的温度分层。当t*=0.1时,不同相变蓄热球位置水箱内的温度分布相似,即水箱底部温度较低,而水箱中上部温度较高,并形成斜温层。此后,随着放水过程的进行,由于相变蓄热球的存在,使得流经蓄热球的水速降低,同时与周围冷流体进行热交换,减弱了水箱中冷热水的混合程度,进而使得水箱的分层效率提高,并且随着相变蓄热球位置的降低,其对冷流体的抑制作用越明显。当t*=1时,相变蓄热球在PCM1,PCM2,PCM3和PCM4的温度分别为 351.69,343.14,337.15,332.15 K,表明在换热过程中相变蓄热球主要以显热的方式与周围的冷流体进行热交换,而并没有完全发生相变过程,其内部的热量也没有得到完全的释放。通过进一步分析图6可知,随着放水过程的进行,等温面(279 K)在水箱中越发平缓,表明由进口冷水带来的冷冲击逐步减缓。此外,当t*=0.1时,各个相变蓄热水箱中等温面(303.15 K)和等温面(348.15 K)的间距均为6.18 cm,随着放水过程的进行,等温面(303.15 K)和等温面(348.15 K)的间距随着相变蓄热球位置的降低而减小,当t*=0.7时,PCM4,PCM3,PCM2和PCM1中等温面(303.15 K)和等温面(348.15 K)的间距分别为 9.28,10.52,11.13,11.75 cm,表明斜温层厚度减小,水箱的热分层程度提高。
这主要是因为当冷流体受到相变蓄热球的抑流和热交换作用,减缓了冷热流体之间的混合进而提高了水箱的热分层程度,且相变蓄热球离底部进水口越近,在t*=0.7时,减缓冷热流体混合效果越明显,热分层效果越好。
4.4 填充因子
相变蓄热球在不同位置时,水箱填充效率随进口流量的变化情况如图7所示。当相变蓄热球在同一位置时,水箱填充效率随着进口流量的增大而减小。当在PCM1,当进口流量为1 L/min时,水箱的填充效率为0.757,而当进口流量增大到9 L/min时,水箱的填充效率下降到0.545。这主要是因为,当流量增大时,进口冷水对水箱内热水的冷冲击增强,冷热水混合程度加剧,水箱内的热分层程度降低,从而减小了水箱的填充效率。此外,随着相变蓄热球位置的降低,水箱的填充效率变大。当流量为 5 L/min时,PCM1,PCM2,PCM3和PCM4的填充效率分别为0.674,0.684,0.699和0.71。这主要是因为,相变蓄热球位置越低,其对进口冷水冲击的减缓作用越明显,进而减缓了水箱内冷热水的混合,因此水箱的填充效率有所提升。此外,由于冷水流过相变蓄热球时会发生热量传递,因而提高了进口冷水的温度,进而提高了蓄热水箱的热分层程度。同时,填充效率的减小幅度随着相变蓄热球位置的升高而变大,即在PCM1时,当进水流量从1 L/min增大到9 L/min时,填充效率减小了28.14%,而在PCM4时,填充效率则减小了21.18%。相同流量下,模拟值要大于实验室,且模拟值和试验值的均方根误差随着相变蓄热球位置的降低而升高。当在PCM1时,模拟值和试验值的均方根误差为0.015,而当PCM4时,模拟值和试验值的均方根误差为0.031。这主要是因为水箱底部冷热水混合,之后在重力等因素作用下,逐渐才形成热分层,因此,相变蓄热球距离进水口越接近,误差值均方根误差越高。
4.5 理查德森数
相变蓄热球在不同位置时,理查德森数Ri随无量纲时间的变化如图8所示。流动稳定时,Ri随进口流量的增加而减小。当在PCM1时,流量为1 L/min时的Ri为870,而当流量增大到9 L/min时,其Ri减小为7。水箱的分层效果随着进口流量的增加而变差,这主要是因为随着进口流量的增加,Re变大,增强了冷热水之间的混合程度,从而导致Ri逐渐减小,水箱的热分层特性变差。随着释热过程的进行,Ri先增大后减小,这表明水箱内的热分层程度先增大后减小。此外,当流量相同时,Ri随相变蓄热球位置的下降而变大。当进口流量为5 L/min时,在PCM1时的Ri为28,而在PCM4时为30,这表明相变蓄热球位置越低,水箱热分层效果越好。此外,进一步分析图8还可以看出,模拟值要大于试验值,模拟值和试验值的均方根误差随着流量的增加而变大,当在PCM4时,流量为1 L/min时模拟值和试验值的均方根误差为0.258,当流量为9 L/min时均方根误差为0.609。同时,模拟值和试验值的均方根误差还随着相变蓄热球位置的降低而增加,当流量为5 L/min,PCM1时模拟值和试验值的均方根误差为0.475,而PCM4时的均方根误差为0.564。
4.6 混合数
如图9所示,相变蓄热球在不同位置时,不同进水流量水箱的混合数随无量纲时间的变化情况。由图可知,水箱的混合数随释热过程的进行均呈先减小后增大的趋势,表明水箱在各个流量下的热分层程度先增大后减小。水箱的混合数在t*=0.05时达到最小,且随着相变蓄热球位置的下降而减小,在PCM4时,进水流量为1,5,9 L/min时的混合数分别为0.013,0.045和0.07;而在PCM1时,其混合数分别为0.02,0.052和0.08。同时,在相同相变蓄热球位置时,水箱的混合数随进水流量的增大而增加,在PCM4时,当进水流量为1 L/min时水箱的混合数为0.082 5(t*=0.5),而当进水流量为9 L/min时为0.457 6(t*=0.5),表明水箱的热分层程度随着进水流量的增加而变弱。进一步分析图9还可知,相同流量下,水箱的混合数随相变蓄热球位置的降低而减小,当进水流量为5 L/min时,PCM1时水箱的混合数为0.316,而PCM4时水箱的混合数为0.246 6。模拟值要略小于试验值,当相变蓄热球位置相同时,其均方根误差随着流量的增加而变大,当在PCM1时,流量为1 L/min时试验值和模拟值的均方根误差为0.201,而当流量为9 L/min为0.513。此外,流量相同时,试验值和模拟值的均方根误差随着相变蓄热球位置的下降而增大,当进水流量为5 L/min时,PCM1时试验值和模拟值的均方根误差为0.335,而PCM4时为0.48。
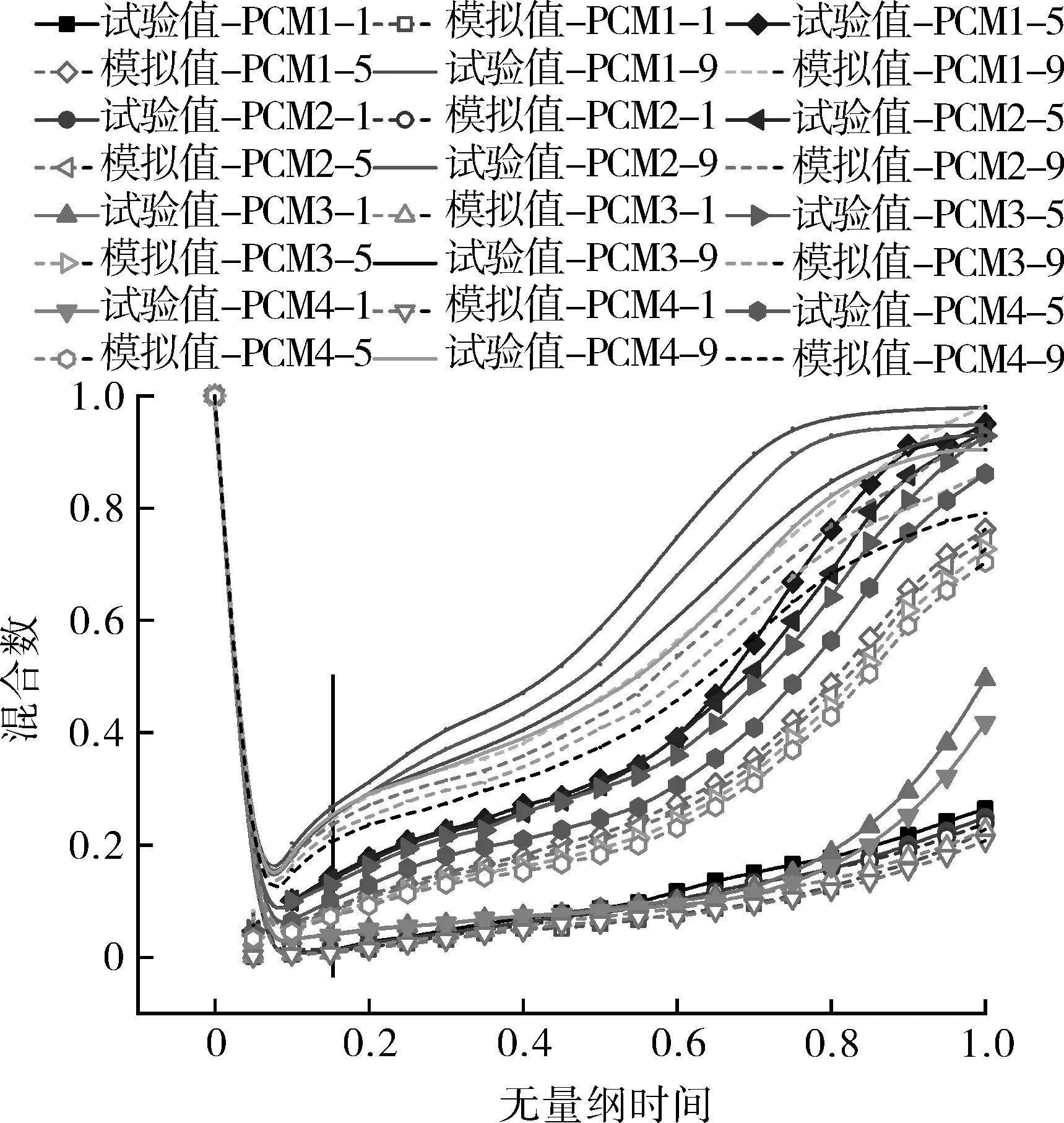
图9 混合数随无量纲时间的变化Fig.9 The variation of MIX number with dimensionless time
5 结论
(1)蓄热水箱内冷热水的混合程度随着相变蓄热球位置的升高而加强,即相变蓄热球越靠近蓄热水箱进口,水箱的热分层效果越好。同时,当t*=1时,相变蓄热球的温度越低,其热量释放的越充分。当冷流体流经相变蓄热球时,由于受到相变蓄热球的抑流和热交换作用,不但减缓了冷热流体之间的混合,同时提高了冷流体的温度,进而提高了水箱的热分层程度。
(2)随着放水过程的进行,等温面(279 K)在水箱中越发平缓,表明由进口冷水带来的冷冲击逐步减缓。此外,当t*=0.1时,各个相变蓄热水箱中等温面(303.15 K)和等温面(348.15 K)的间距均相同,而随着放水过程的进行,等温面(303.15 K)和等温面(348.15 K)的间距随着相变蓄热球位置的降低而减小,当 t*=0.7 时,PCM4,PCM3,PCM2 和PCM1中等温面(303.15 K)和等温面(348.15 K)的间距分别为 9.28,10.52,11.13,11.75 cm,表明斜温层厚度减小,水箱的热分层程度提高。
(3)填充效率和理查森数的模拟值略大于试验值,而混合数的模拟值略小于试验值。随着进水流量的增加,填充效率和理查森数减小,而混合数增大。填充效率、理查森数和混合数试验值和模拟值的均方根误差随着相变蓄热球位置的下降和进水流量的增加而增大。

