变工况往复压缩机曲轴的模型构建与动力学分析

王金铭 ，马 茵 ，程贵健 ，王 瑶 ，3，江志农 ，3

（1.北京化工大学 高端机械装备健康监控与自愈化北京市重点实验室，北京 100029；2.大庆石化公司炼油厂 加氢二车间，黑龙江大庆 163700；3.北京化工大学 压缩机技术国家重点实验室压缩机健康智能监控中心，北京 100029）

0 引言

往复压缩机在石油化工及天然气管道运输等行业的应用极为广泛，但传统往复压缩机存在流量固定、与末端需求气量不匹配的不足，能源成本占总成本达65%，因此为压缩机引入无级气量调节系统，采用部分行程顶开进气阀的气量调节方式，使其可以灵活适应压缩机末端气量需求，从而节省大量资源［1-3］。但由于部分行程顶开进气阀的调节方式改变了往复压缩机各部件原本的运动特性及受力状态［4］，由此引发的各部件故障失效问题频频发生［5］，造成不可预估的压缩机故障损失。

曲轴作为往复压缩机传动机构的核心部件，决定了压缩机的承载能力，直接影响着压缩机整机的运行状态。气量调节工况下的变负荷运行改变了气缸内的气体力变化规律，破坏了其本身的动平衡关系，这对其变形及强度均会产生影响，甚至可能导致其过早地发生疲劳失效。为研究气量调节工况对曲轴特性所产生的具体影响，必须对曲轴的特性进行有效的分析，以便对压缩机进行具有针对性的参数优化以延长其使用寿命。对于曲轴的特性分析通常采用力学分析与有限元仿真相结合的方法，通过分析曲轴的受力关系获得曲轴所受的交变载荷［6］，结合静力学模拟对曲轴进行变工况条件下的特性研究［7-8］。由于曲轴受交变载荷作用，其受力以及受力面在整个周期内变化频繁，通过传统的静力学有限元分析法不仅计算量大，且难以完整准确地表述出曲轴在整周期内的特性变化。

本文采用力学分析法与多体动力学刚柔耦合分析法相结合的研究方法［9-15］，以某六缸双作用多级往复压缩机曲轴为研究对象，对其传动机构在气量调节正常工况以及故障工况下所受的整周期交变载荷以及曲轴在交变载荷作用下的特性进行分析，避免了由于曲轴载荷及受力面变化所导致的计算偏差以及计算量大等问题。

1 曲轴的力学模型构建

本文所研究往复压缩机为六缸双作用多级往复压缩机，其传动机构的曲轴由三对双拐轴组成，其中曲轴的第1，3和5列轴颈连接一级气缸，称为一级连杆轴颈，第2，4列为二级连杆轴颈，而第6列轴颈为三级。机组的进气压力为0.13 MPa，一级排气压力为0.33 MPa，二级排气压力为0.82 MPa，最终排气压力为1.4 MPa。

1.1 单列曲轴力学模型

往复压缩机的传动机构各部件运动关系及受力情况如图1所示。建立单列曲轴的力学模型用于获取曲轴上的载荷分布，以便于对其进行后续特性分析。

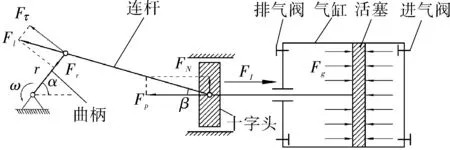
图1 传动机构运动关系Fig.1 Kinematic relationship of transmission mechanism

1.1.1 气体力

气量调节工况下压缩机工作循环包含以下5个阶段：膨胀、吸气、回流、压缩和排气阶段。对各阶段压缩机工作过程做以下几项假设：气体为理想气体且稳定流动，气体压缩过程为绝热压缩，压缩腔内的热力学性质只依赖时间变化，忽略气体在气阀入口处能量损失和压力波动。通过建立气缸热力学微分方程获得各阶段气缸内实时的压力变化情况如下［1］。

式中 pcy——缸内气压；

Vc——缸内气体容积；

pexp——排气终了压力；

Vcle——余隙容积；

me——膨胀过程指数；

ps，pd——吸气、排气 压力；

αsAs——进气阀有效通流面积；

αdAd——排气阀有效通流面积；

R ——气体常数；

Ts——吸气腔内气体温度；

Vs——吸入气体体积；

mc——压缩过程指数；

Td——排气阀腔内气体温度。

在刚柔耦合模型中对活塞施加的综合气体力为盖侧气体力与轴侧气体力的矢量和：

式中 G ，Z ——下标，盖侧、轴侧；

A ——活塞端面面积。

根据往复压缩机5个阶段的气体力方程计算得出气量调节工况下活塞所受到的综合气体力如图2所示。随着负荷逐渐降低，卸荷器顶开进气阀时间逐渐延长，气体力随之发生变化，而气体力的变化将导致曲轴所受到的交变载荷相应发生变化，改变了曲轴原本的动平衡状态，使得曲轴的变形及应力状态等特性发生变化。

图2 变负荷条件下缸内综合气体力Fig.2 Comprehensive gas force under variable load

1.1.2 连杆力

如图1所示，连杆力Fl是由活塞通过活塞杆、十字头传递到连杆上的力，与曲轴的连杆轴颈相互作用。综合活塞力是气体力Fg、往复惯性力FI和往复摩擦力Ff的矢量和，将综合活塞力按照活塞杆、连杆和曲柄之间的角度关系进行计算分解即可得连杆力［6］。

活塞的往复惯性力为［6］：

活塞的往复摩擦力为［4］：

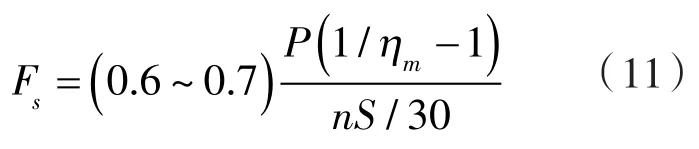
式中 mp——往复惯性质量；

r——曲轴旋转半径；

ω——曲轴旋转角速度；

α——曲轴转角；

λ——连杆比，λ=r/l；

P ——指示功率；

ηm——机械效率；

n——曲轴转速；

S——活塞行程。

将综合活塞力Fp分解为沿连杆方向的连杆力 Fl和侧向力 Fh［6］。

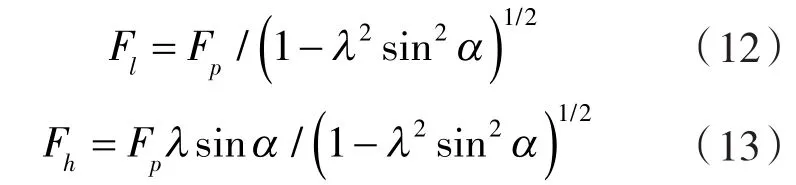
连杆力Fl作用于曲轴上，可分解为径向力Fr和切向力FFτ［6］。

1.2 曲轴整体受力

曲轴整体受力如图3所示，经力学分析，曲轴主要受到的外力是由连杆力引起的阻力矩My和电机驱动力矩Md组成［6］。

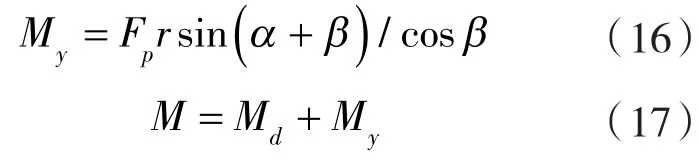
图3 曲轴整体受力分析Fig.3 Force analysis of the whole crankshaft

曲轴合外力矩的值等于转动惯量与其瞬时角加速度的乘积，mk是全部旋转质量的质量和，因此曲轴的合外力矩可表示为［6］：

式中 J ——曲轴质量转动惯量；

rk——各不平衡质量旋转半径；

ε ——曲轴瞬时角加速度。

曲轴若想实现匀速运动需采用飞轮平衡或补充多余能量［6］，飞轮矩的值为：

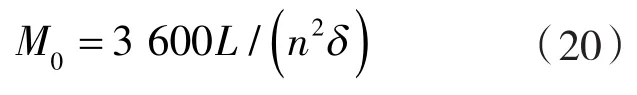
式中 L ——压缩机一周期内的能量变化值；

δ ——旋转不均匀度。

曲轴的切向力与径向力分别与轴承支撑力的矢量和为0。曲轴的力矩平衡方程结合其切向力与径向力的力平衡方程可得各轴承处的支反力以及曲轴各截面的力矩。

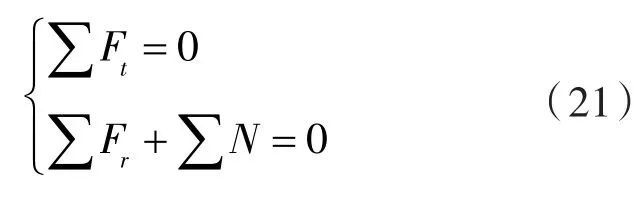
从力学分析结果可以看出，曲轴所受到的连杆力会对曲轴的承载能力有直接影响，并进一步影响其使用寿命。

2 仿真模型的建立

2.1 刚体模型的构建

利用SolidWorks建模软件建立往复压缩机传动机构的三维实体模型，并将模型以x_t的格式导入Recurdyn软件中，根据各部件间的运动关系，为模型添加合适的约束及运动副，见表1。

表1 各部件约束类型Tab.1 Constraint types of components

2.2 刚柔耦合模型的建立

将曲轴三维模型导入ANSYS，并设置45钢对应的材料属性，选用Solid185单元对曲轴模型进行网格划分，最终曲轴被划分为64 530个单元以及14 039个节点。在曲轴每对双拐轴的主轴承中心处建立刚性节点，共计3个刚性节点，并且以3个刚性节点分别为主节点创建刚性连接，随后完成RFI文件的导出。将RFI文件导入Recurdyn软件中生成柔性体文件，并替换原有的刚性曲轴［11］，最终形成的多体动力学刚柔耦合模型如图4所示。

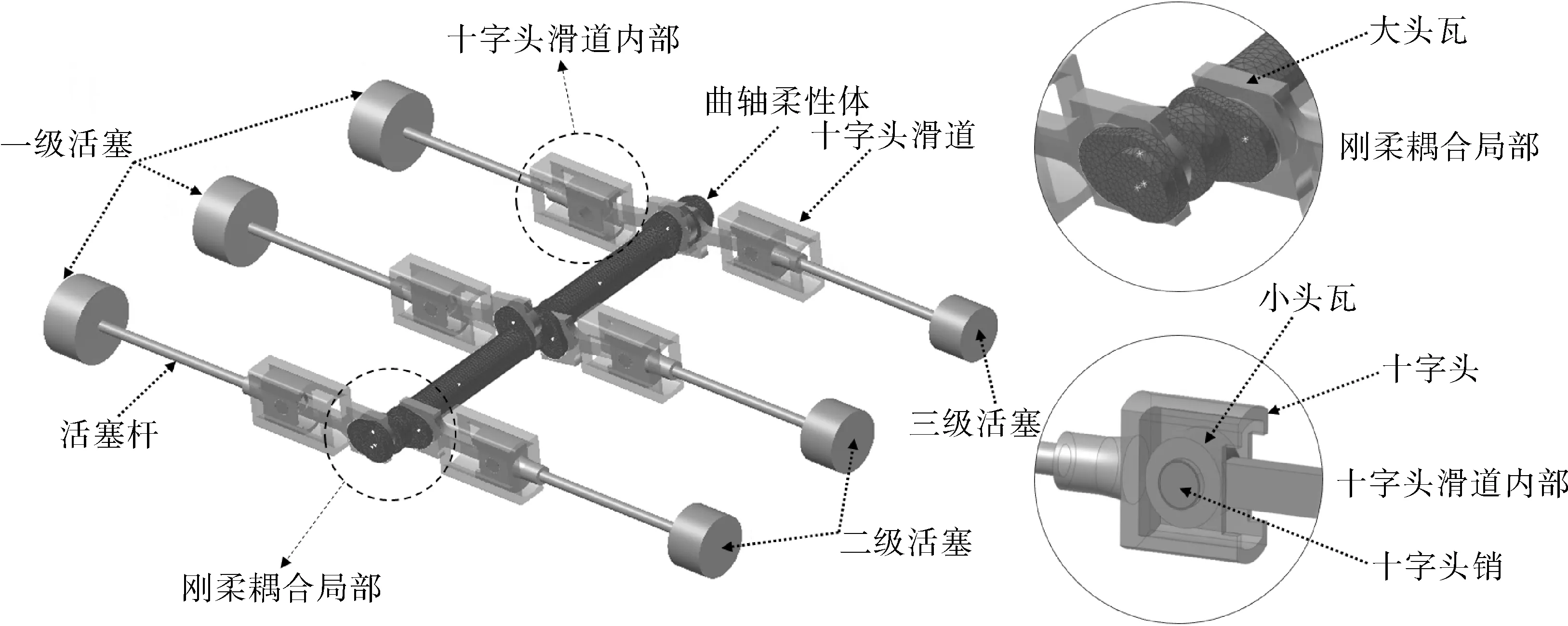
图4 压缩机传动机构刚柔耦合模型Fig.4 Rigid-flexible coupling model of compressor transmission mechanism

2.3 施加载荷

对于正常气量调节工况，将通过力学模型计算所得到的10%～100%负荷下整周期的综合气体力以10%为间隔提取工况点，作用于各级活塞。对于气量调节的故障工况，将其分为级内和级间两种负荷调节偏差的故障情况分别进行模拟，均以50%负荷作为基础负荷且三级气缸出现负荷偏差为例，级内偏差将三级气缸设置为其盖侧负荷比轴侧低5%～40%，级间偏差的故障工况分别将三级气缸低于其他气缸5%～40%，故障工况点间隔为5%。曲轴转速设定为333 r/min，步数为720。

3 结果分析

3.1 气量调节正常工况

3.1.1 变形分析

对于刚柔耦合中的模态柔性体，其变形通过每一时刻物体的弹性位移来描述［11］，提取曲轴各列连杆轴颈上部分节点变形量进行后续分析。仿真结果显示曲轴在变负荷条件下各级轴颈的最大变形通常出现在连杆轴颈的中部，其中某一时刻曲轴的变形情况如图5所示。

图5 气量调节正常工况下某一时刻曲轴变形Fig.5 Crankshaft deformation at a certain time under normal condition of air volume regulation

在气量调节正常工况下各级轴颈变形量随负荷变化规律如图6所示。

图6 变工况条件下轴颈变形量Fig.6 Journal deformation under off design condition

随着负荷降低，各级轴颈变形量出现较为明显的变化。一、二级轴颈变形规律相似，负荷高于36%以上时两级轴颈变形量均低于100%额定负荷，而低于36%负荷时两级轴颈变形量逐渐高于额定负荷。变负荷条件下运行的三级轴颈变形量均低于额定负荷。

3.1.2 应力分析

经仿真得到某一时刻曲轴上的应力分布如图7所示。曲轴整体上曲轴中部的两列轴颈上的应力较大，且应力集中主要发生在各断面连接处附近，提取每列轴颈上应力较为集中的节点处应力值进行后续分析。

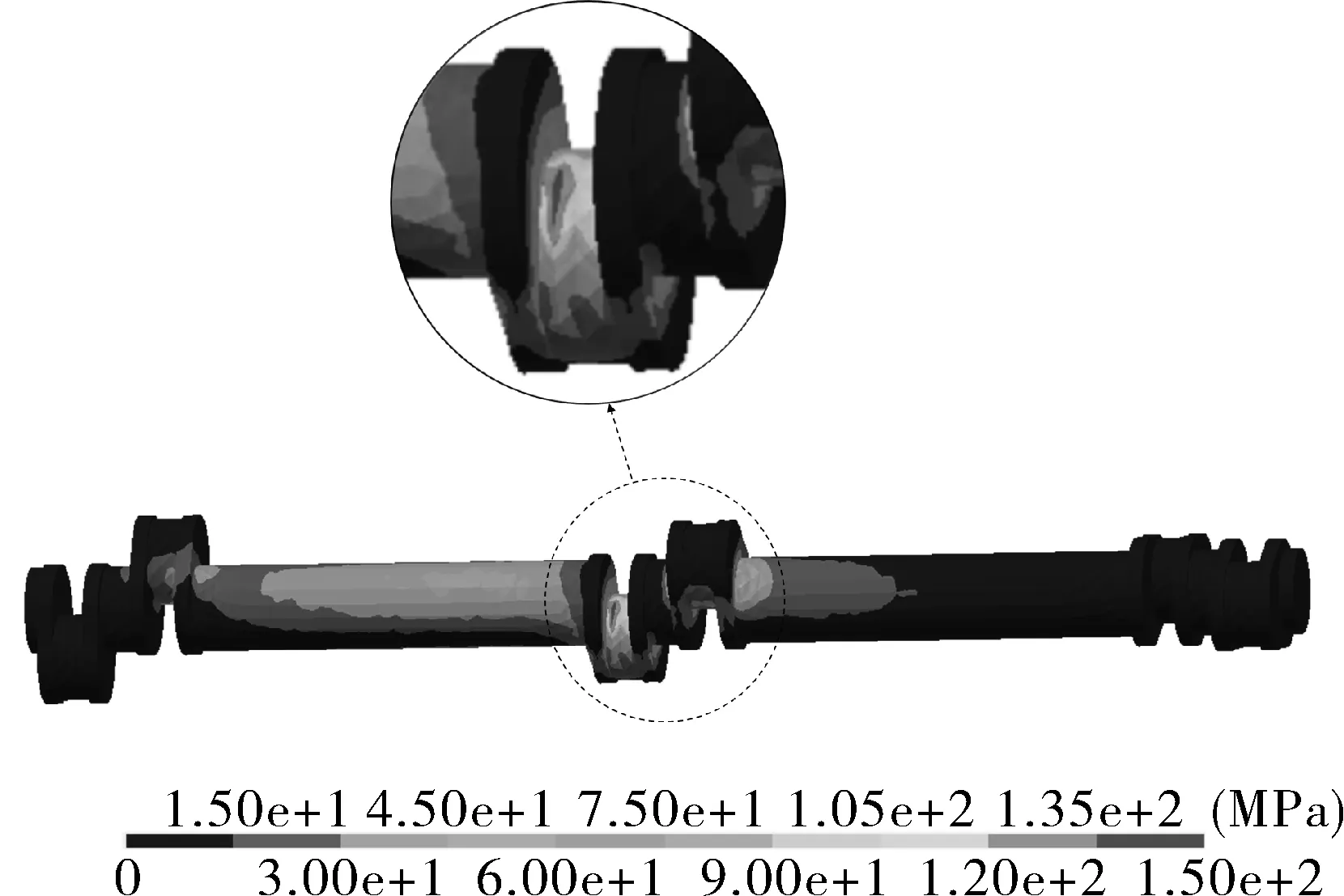
图7 曲轴应力分布Fig.7 Stress distribution of crankshaft

变负荷对其应力变化所产生的影响如图8所示，随着压缩机工作负荷逐渐降低，一级轴颈应力值在100%降至85%负荷的过程中应力值逐渐增加，随后变化趋于平缓，而在低于45%负荷后应力值继续增加，最终达到最大值176.48 MPa。二级轴颈处的应力值在30%负荷以上时普遍低于额定负荷，而在30%以下时略高于额定负荷。三级轴颈应力值受负荷影响不明显。

图8 变工况条件下最大应力值Fig.8 Maximum stress value under off design condition

3.2 级内负荷调节偏差

多级双作用往复压缩机的每个气缸都由轴侧和盖侧两个工作腔组成，如图9（a）所示，两侧气缸均周向分布式布置有多个进气阀，如图9（b）所示。多个进气阀同时决定了该气缸内的负荷，当某一进气阀上的气量调节装置出现性能退化、电磁阀故障或控制信号不统一差等问题时就会使缸内气体力发生变化，从而造成气缸内活塞两侧出现负荷调节偏差，级内负荷调节偏差如图9（a）所示。

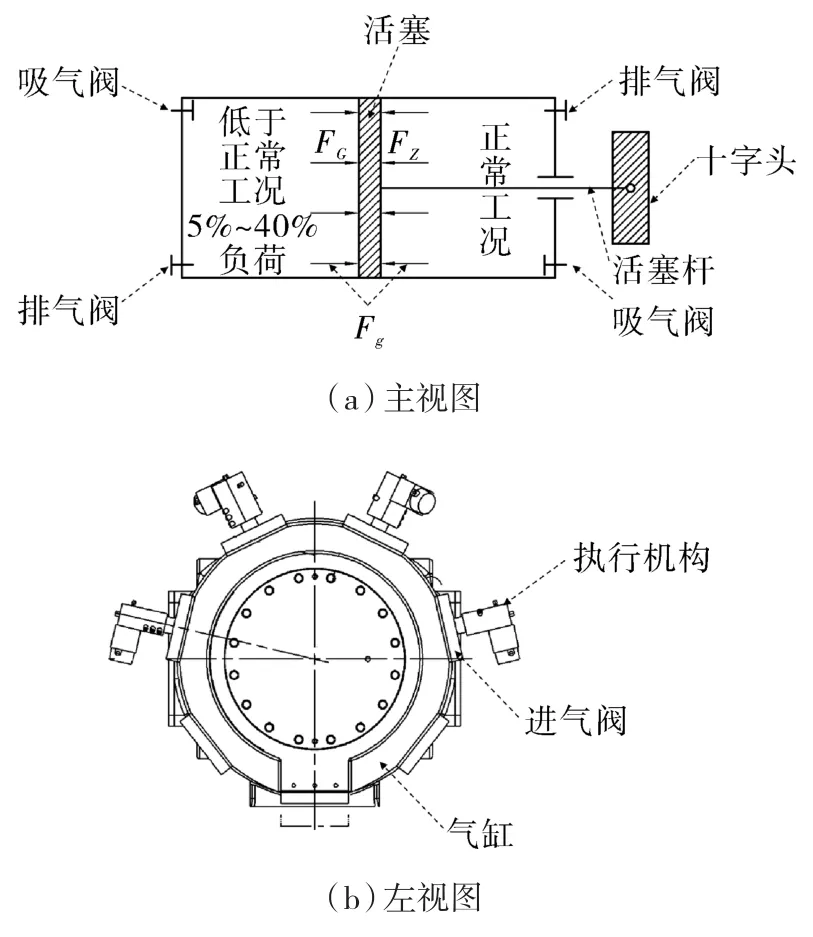
图9 气缸结构示意Fig. 9 Schematic diagram of cylinder structure

3.2.1 变形分析

负荷偏差对曲轴所产生的影响，用不同负荷偏差下各级连杆轴颈的变形量及应力相对于无偏差状态下的变化率来表示，其中变形量的相对变化率如图10所示。

图10 级内偏差条件下变形量相对变化率Fig.10 Relative change rate of deformation under the condition of intra-stage deviation

级内偏差对一二级轴颈变形量影响较大。一级轴颈在偏差状态下的变形量高于无偏差状态，除15%偏差外其余偏差下持续增长，最大值达0.455 1。二级轴颈在小于8%的偏差范围内变形量小于无偏差状态，高于8%后相对变化率持续增长，且在15%后超过了一级轴颈，最大值达到0.5181。级内调节偏差对三级轴颈的影响较小，仅在25%以上时其相对变化率出现较小幅度的增长。

3.2.2 应力分析

级内负荷调节偏差对各级轴颈的应力值影响变化规律如图11所示，一级轴颈应力值在负荷调节偏差时均低于无偏差状态，二级轴颈在偏差大于8%时应力值逐渐高于无偏差状态，其相对变化率在20%后趋于平缓。三级轴颈应力值在0～10%和33%～40%两个负荷偏差区间内高于无偏差状态，其余范围内应力值变化率小于0。

图11 级内偏差条件下应力值相对变化率Fig.11 Relative change rate of stress value under the condition of intra-stage deviation

3.3 级间负荷调节偏差

3.3.1 变形分析

相比级内偏差，级间负荷偏差使曲轴受力不平衡的情况加剧，其变形量变化规律如图12所示，各级轴颈变形量相对变化率变化规律相似。一级轴颈在偏差小于10%范围内的变化率增长较小，在10%～20%范围内急速增长，20%～30%再次经历平缓阶段，而30%以上变化率增长且最终达到最大值0.990 1。二级轴颈的变形量在10%的偏差范围内小于无偏差状态，在10%以上时其变化规律与一级轴颈相似，在15%以上是其变化率超过一级轴颈，最终达到1.111 3。三级轴颈的变形量变化趋势与二级相似，最大为0.303 2。

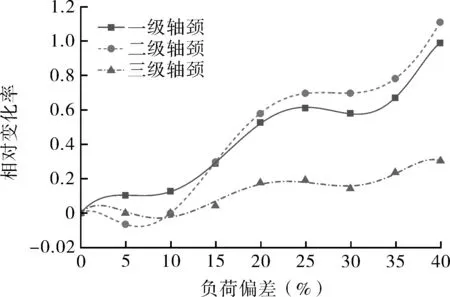
图12 级间偏差条件下变形量相对变化率Fig.12 Relative change rate of deformation under the condition of interstage deviation

3.3.2 应力分析

级间负荷调节偏差对轴颈应力变化的影响如图13所示，偏差状态下的一二级轴颈应力值均小于有偏差状态，三级轴颈在负荷偏差0～12%和32%～40%两个负荷区间内的应力值变化率大于0，其余范围内的应力值均低于无偏差状态。

图13 级间偏差条件下应力值相对变化率Fig.13 Relative change rate of stress value under the condition of interstage deviation

4 结论

（1）在气量调节正常工况下，压缩机变负荷运行对曲轴的变形及应力值均会产生影响，其中变负荷对曲轴一二级轴颈的影响较大。

（2）对于气量调节的故障工况，级内和级间偏差均会对曲轴的变形产生较大影响，而对应力影响不明显，其中级间偏差对曲轴所产生的不利影响明显大于级内偏差。

（3）结合分析不同负荷偏差对曲轴连杆轴颈变形量和应力值所产生的影响，气量调节正常工况需尽量避免在36%负荷以下长期运行，级内负荷调节偏差应控制在15%范围内，级间负荷调节偏差应控制在10%，否则将致使曲轴产生较为明显的恶化。