张量环因子非凸秩约束的高光谱图像超解析
郑建炜,周鑫杰,徐宏辉,秦梦洁,白琮
(浙江工业大学计算机科学与技术学院,杭州310023)
0 引言
超谱图像(Hyperspectral Image,HSI)由多个特定频率的离散波段组成,不仅包含了丰富的光谱信息,而且可以提供人眼无法捕捉到的真实场景,有助于目标的准确识别,已被广泛应用于如压缩感知[1-2],目标分类[3]等地球遥感任务中。然而,受限于太阳辐照度,光学成像机理等因素,设备在采集图像时通常会牺牲部分空间分辨率以保证其获得较高的光谱分辨率,极大限制了光谱图像的后续处理及应用精度。与HSI相反,由多光谱传感器获得的多光谱图像(Multispectral Image,MSI)具有较高的空间分辨率但光谱分辨率较低。目前,将同一空间场景下的高空间分辨率多光谱图像(High spatial Resolution Multispectral Image,HR-MSI)和低空间分辨率的高光谱图像(Low spatial Resolution Hyperspectral Image,LR-HSI)进行融合来生成高空间分辨率的高光谱图像(High spatial Resolution Hyperspectral Image,HR-HSI)是实现HSI超分辨率重构的常用方法。
HSI的光谱维度包含了同一空间场景不同光谱波段内的成像结果,故不同光谱通道之间存在着高度的相关性,即光谱低秩先验。基于此结论,早期HSI-MSI融合方法都将三维HSI展开为二维矩阵,利用矩阵分解[4-6]将高光谱图像映射到一系列正交基上,通过对系数施加先验约束达到融合目的。如DONG Weisheng 等[5]提出一种非负结构稀疏表示(Nonnegative Structured Sparse Representation,NSSR)方法,通过从LR-HSI中学习一个光谱正交基矩阵,并利用系数矩阵的稀疏先验,取得了较好的重构效果。SIMOES A 等[7]在使用子空间表示的基础上,结合了全差分正则项以利用HSI的空间平滑信息。然而高光谱图像本质上是一种具有两个空间维度和一个光谱维度的三维数据,将多维HSI数据转化为矩阵通常会破坏其光谱-空间的结构相关性,降低模型性能。
张量表示可以有效保留光谱图像固有的结构信息,目前基于张量分解[8]的方法也已成为解决HSI-MSI融合问题的有效方案之一。DIAN Renwei 等[9]提出了一种基于非局部稀疏张量表示的HSI 超解析方法,通过将HR-MSI 与LR-HSI 划分成多个堆叠的三维patch,然后利用图像的非局部相似性将相似的patch 聚类到同一个簇中,在稀疏张量分解的三个字典模式下重构HR-HSI。之后,LI Shutao 等[10]提出了一种耦合稀疏Tucker分解(Coupled Sparse Tucker Decomposition,CSTF)算法,将HR-HSI 与LR-MSI 均分解成一个因子与三个模字典,并应用近端交替算法优化求解。XU Ting 等[11]提出了单向全变差(Unidirectional Total Variation,UTV)模型,在CSTF 的基础上,利用了全变差正则项刻画三个模矩阵的分段光滑特性。WANG Kaidong 等[12]提出了一种结合非局部低秩张量分解与光谱分解的HSI 超解析方法,通过应用张量分解方法描述聚类簇张量的低秩特性,并结合光谱线性分解的方法对丰度矩阵施加非凸约束以避免光谱失真问题,取得了良好的重构效果。上述基于Tucker 分解的方法虽然都较好保留了光谱图像的光谱-空间相关性,有效保持了图像的光谱结构。但Tucker分解的空间复杂度会随张量阶数N的增加呈指数级增长,容易造成维度灾难问题。
基于张量网络的方法如张量链(Tensor Train,TT)分解[13],张量环(Teansor Ring,TR)分解[14]具有比其他分解更强的挖掘数据内在结构的能力。DIAN Renwei 等[15]通过利用非局部相似性,将图像中的相似patch 聚类形成多个4 维张量,在此基础上,对这些4 维张量施加张量链分解正则项,取得了不错的重构效果。然而,TT 分解需要对边界的因子施加秩-1 约束,导致其表达能力和灵活性受到限制。HE Wei 等[16]再结合全差分正则项,将张量环分解引入到遥感图像修复任务中,提出了一种用于遥感图像缺失信息重构的TR 填充方法,取得了优异的性能。相对而言,TR 可以看作一组TT 表示的线性组合,得益于其因子可以在迹运算下等价处理,TR 分解克服了TT 分解的局限,具有更强的灵活性。
近年来,部分研究者对张量环因子的潜在属性进行了探索,如YUAN Longhua 等[17]建立了张量秩和张量环因子秩之间的理论关系,并基于此对因子施加核范数约束,提出了张量环低秩因子模型。HE Wei等[18]提出了一种基于TR 分解的HSI-MSI融合模型,并对其中第三个因子施加了低秩核范数约束。虽然这些方法都取得了令人满意的结果,但仍存在两个问题。首先,这些模型都将因子展开为n模矩阵,忽视了其不同模式间的相关性;其次,矩阵核范数约束试图在基于矩阵奇异值分解(Singular Value Decomposition,SVD)的向量空间中对张量进行建模,其最优性表示会受到一定损失[19]。基于t-SVD(tensor-Singular Value Decomposition,t-SVD)的张量核范数(Tensor Nuclear Norm,TNN)[20]可以有效保持张量固有的低秩结构,同时避免张量矩阵化过程中的原始信息损失[19]。然而,图像中较大的奇异值通常对应于主要信息,如轮廓,锐边和平滑区域[21],但TNN 平等的对待每一个奇异值,意味着较大的奇异值受到的惩罚较大,这在实际应用中会导致主信息丢失和次优解。受到对传统压缩感知恢复的启发,利用非凸函数[22]代替l1范数去逼近秩函数,能更准确从退化的HSI中提取低秩分量,并且使得较大的奇异值受到较少的惩罚,可有效保留图像数据的主要信息。
因此,针对HSI-MSI融合问题,本文结合高光谱图像的全局谱低秩性与非局部相似先验,在张量环分解的基础上提出了一种基于非凸张量秩约束的低秩张量环分解(Low-Rank Tensor Ring decomposition based on Log-Tensor Nuclear Norm,LRTRLogTNN)正则项,通过直接对因子施加基于t-SVD的非凸张量核范数约束,进一步挖掘高光谱图像的内在低秩结构。具体而言,首先利用高光谱图像的全局谱低秩性将其投影至低维紧致空间,再结合降维后HSI的空间非局部相似性将其分成多个patch并逐个实施相似目标搜索以形成三维张量组。进一步,使用张量环分解技术挖掘其内在低秩结构,同时探索张量环因子的本质特征。不同于文献[17]与[18]将因子展开为矩阵并施加核范数正则项的方式,本文提出直接以张量形式对每个因子施加基于t-SVD 的张量核范数约束,充分探索其固有的低秩结构并有效避免张量因子矩阵化过程中存在的结构信息丢失等问题。此外,针对TNN 中使用l1范数所导致的图像主信息丢失和次优解等缺陷,本文引入log函数代替l1范数,避免较大奇异值受到过度惩罚,能更准确的逼近其本质秩函数,实现高光谱图像的超解析重构。大量实验结果表明,所提方法有效地提高了恢复图像的质量,与现有最新的融合方法相比,该算法在定量评价与可视化对比中都有更好的表现。
1 相关工作
1.1 张量概念及符号说明


1.2 基于低秩子空间表示的HSI-MSI 融合框架

1.3 基于t-SVD 的张量低秩表示

2 算法提出与优化
2.1 LRTRLogTNN 正则项


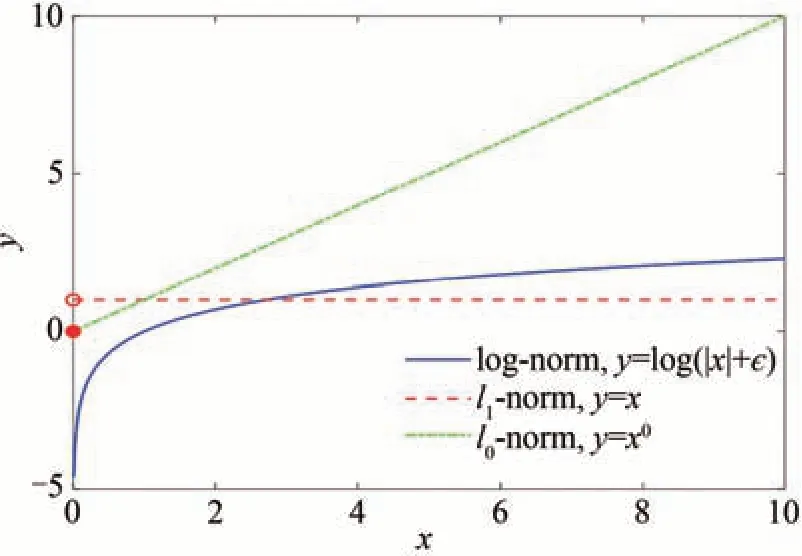
图1 l0 范数、l1 范数和log 函数比较Fig.1 Comparison of l0-norm,l1-norm and log function

式中,η是一个平衡参数。作为张量低秩的非凸松弛,LogTNN 比TNN 更能逼近本质秩函数,可以有效压制超分过程中所带来的噪声和异常结构,得到具有光滑性光谱结构的清晰HR-HSI。
2.2 联合非局部相似先验与LRTRLogTNN 的HSI-MSI 融合模型
HSI 不仅在光谱以及空间维度存在低秩性,在图像域中也存在强相关性,即非局部相似性[29]。因此本文对融合问题也施加此先验,通过将图像相似patch 进行聚类以充分利用图像的内在低秩性。具体来说,利用HR-MSI 的空间信息,将降维后的HSI 分割成多个三维pacth,在图像全域范围搜索与之结构相似的patch 并重构成新的低秩三阶张量,然后利用LRTRLogTNN 正则项挖掘其低秩属性,图2 为本文方法的流程说明。综合上述分析,所提的联合非局部相似先验与LRTRLogTNN 约束的HSI-MSI 融合模型为

图2 所提方法整体框架Fig.2 Flowchart of the proposed method.
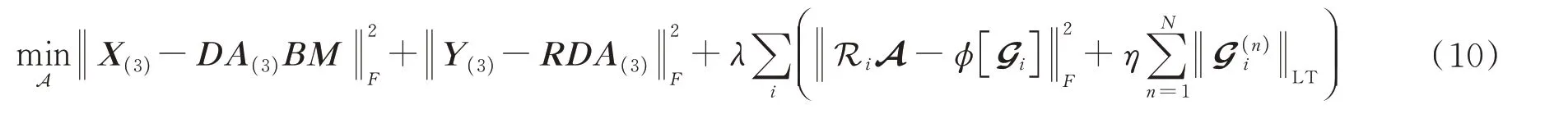
式中,RiA表示在A空间位置i处经patch 分组形成的三阶张量。与现有的HR-HSI 图像融合方法相比,本文提出的LRTRLogTNN 模型有两个显著的优点:首先通过从LR-HSI 中学习低维子空间,充分利用了高光谱图像的全局谱低秩先验,并从降维后的图像中提取了非局部相似的三维pacth 组,探索了HSI 的空间非局部相似性。另一方面,对低秩张量因子施加LRTRLogTNN 正则项能更真实的表示所构造张量的结构相关性,并实现对张量秩函数的稳健逼近。
2.3 模型的优化与求解



表1 式(12)中A( 3 )的闭式解Table 1 The closed form solution for Eq.(12)




表2 基于ADMM 算法的LRTRLogTNN 模型求解Table 2 Solution of LRTRLogTNN model via ADMM algorithm
3 实验结果与分析
为全面评估本文所提LRTRLogTNN 算法的有效性,选择三组数据并与其他算法进行实验对比。第一组高光谱数据是用数字图像采集试验仪拍摄的Washington DC Mall,其空间尺寸为1 208×307×191,如图3(a)所示。由于内存空间限制,本文实验仅使用整个HSI 的一个子区域,其空间尺寸为256×256×103。第二组数据为Pavia City Center,原始空间尺寸为1 096×1 096×102,如图3(b)所示,本文选取了其中大小为200×200×80 的子块进行实验。第三组数据为Cuprite Mine,其原始空间尺寸为512×614×224,如图3(c)所示。在去除低信噪比以及被水蒸气吸收波段之后,选取了其中的89 波段,具体尺寸为200×200×89。同时为了便于数值计算和可视化,本文将HSI 所有波段归一化为[0,1],待重构后恢复拉伸至原始水平。

图3 实验所用三个数据集Fig.3 Three data sets were used in the experiment
本文选取了四种HSI-MSI 融合方法进行比较,其中包括NSSR 方法[5],CSTF 模型[10],LTMR 方法[24]以及UTV 模型[11]。针对每个数据集,为模拟LR-HSI,首先用标准差为2 的7×7 高斯模糊核对HR-HSI 的每个波段进行滤波,然后在空间域中对其中每四个像素进行下采样,即选取dw×dh=2×2。对于模拟同一场景的HR-MSI,本文使用类似IKONOS 光谱响应滤波器[36]维度对HR-HSI 下采样,最后采用包含4 个波段的HR-MSI 进行模拟。
3.1 评价指标
为了定量对比不同方法的融合效果,采用8 个常用的图像超分辨率重构评价指标,分别为:峰值信噪比(Peak Signal-to-Noise ratio,PSNR)[9],结构相似度(Structural Similarity Indices,SSIM)[32],通用图像质量指数(Universal Image Quality Index,UIQI)[33],互相关性(Cross Correlation,CC)[8],光谱相似度(Spectral Angel Mapper,SAM)[34],相对无量纲整体误差(The Relative Dimensionless Global Error in Synthesis,ERGES)[35],失真度(Degree of Distortion,DD)[10]和均方根误差(Root Mean Square Error,RMSE)[12]。此外,将高光谱图像各个波段的PSNR 值与SSIM 指标平均,得到平均峰值信噪比(MPSNR),平均结构相似度(MSSIM)。在指标MPSNR,MSSIM,UIQI 与CC 下,其值越大,表示融合效果越好。指标DD,SAM,ERGAS,RMSE 的理想值均为0,意味着其值越小,融合效果越好。
3.2 参数分析
在所提LRTRLogTNN 模型中,张量环秩R与平衡参数η的值需要预先确定。本文对这两个参数进行了实验分析以保证模型的最佳性能。R是一个重要的参数,预先设定的R值过高或过低都会直接影响恢复HR-HSI 的精度。为便于参数分析,假设不同因子的秩均相等,即R1=R2=…=RN,图4 表示了Pavia City Center 数据集在不同的R值下,所融合得到图像的MPSNR 值变化。从图4(a)可以看出,当参数R在2到11 之间变化时,MPSNR 值会逐步上升。但当超过峰值11 时,模型的性能会随着R的进一步增大而迅速下降。图4(b)表示了在该数据集下,η值在[0~1]×10-3范围内的变化对融合结果的影响。分析图4(b)的结果可知,在该范围内,随着参数η值逐渐逼近0.001,MPSNR 逐渐趋于一个稳定值,但当η达到0.000 7 时,取得了最高的MPSNR 数值。综上分析,本文选取最优参数R=11,η=0.000 7 进行实验后续实验对比。

图4 不同参数R 与η 对MSPNR 值的影响Fig.4 Effect of different parameters R and η on MSPNR results
3.3 实验结果分析
分别通过表3~5 展示了五个方法在三个数据集上的定量融合效果,各个评价指标MPSNR、MSSIM、UIQI、CC、SAM、ERGAS、DD 和RMSE 的值如表所示,其中加粗字体表示最优值。图5 是Cupriter Mine 数据集第21 个波段的重构图像及其误差图的可视化结果。图6 为不同对比算法在三个数据集中不同波段下的PSNR 值。

表3 Cuprite Mine 数据集下五个算法的定量评价指标结果Table 3 Quantitative evaluation results of all test methods in Cuprite Mine data set
对于Cupriter Mine 数据集,从表3 可知,LRTRLogTNN 在所有指标上都取得了最优值。具体而言,LRTRLogTNN 的MPSNR 值比NSSR,CSTF,UTV,LTMR 分别领先了5.195 3 db,3.655 6 db,1.783 9 db以及0.431 0 db。由于NSSR 方法仅利用矩阵分解的方法,忽视了高光谱图像作为三维数据的光谱-空间结构相关性,因此取得了最差的效果。CSTF,UTV 则采用了张量分解的处理方式,UTV 在CSTF 的基础上对模字典矩阵施加了全变差约束,进一步利用了模矩阵的空间平滑先验,相对而言重构效果更好,然而Tucker 分解的方式并不能充分挖掘张量数据的内在结构信息。LTMR 则在考虑到子空间表示的基础上,结合了光谱图像的非局部相似性,并利用张量秩函数对聚类张量进行约束,取得了比其他三个算法更好的结果。相较于LTMR,本文模型结合了子空间低秩表示与非局部相似先验,利用张量环分解挖掘光谱图像的内在结构信息,并对张量环因子施加非凸张量秩函数约束,进一步探索了光谱低秩先验,因此在各个指标值下都有较高的提升。图5 给出了Cupriter Mine 数据集第21 个波段的重构图像及其误差图的可视化结果,同时选取了代表性的区域进行放大。误差图可以有效体现融合后的HR-HSI 与原始HSI 的误差,其中较深的蓝色表示融合效果更接近原始HSI。图5 的结果表明,虽然各个方法都较好的重构了HR-HSI,但从第二行误差图及其放大区域可知,本文方法取得的结果中浅色区域较少且蓝色区域颜色相对更深,重构表现优于其他对比算法。图6(a)的结果进一步表明所提算法在各波段的PSNR 值均高于其他算法,验证了所提算法的优越性。

图5 第一行为Curpriter Mine 数据集第21 个波段的重构结果可视化对比,第二行为相应误差影像Fig.5 The first line gives the visual comparison of the reconstruction results at the 21th band of the Curpriter Mine dataset,and the second line shows the related error images
在Washington DC Mall 数据集上,由表4 可知,LRTRLogTNN 同样在所有评价指标上取得了最优值。为更进一步直观地比较各个方法的效果差异,图7 给出了Washington DC Mall 数据集第80 个波段的重构图像及其误差图的可视化结果,同时选取了代表性的区域进行放大。从图7 第一行可以看出,所有方法都能从HR-MSI 中学习到较好的空间细节,各个方法的视觉差异不大,但从第二行的误差图及其放大区域可知,本文所提方法整体表现出了更深的蓝色,且在边缘与纹理中仅有少量散乱点,因此取得了更优的结果。图6(b)表明,LRTRLogTNN 仅出现个别波段的PSNR 值低于LTMR 方法,但整体定量重构结果较之于各对比算法依然表现出明显的优势。

表4 Washington DC Mall 数据集下五个测试方法的定量评价指标结果Table 4 Quantitative evaluation index results of testing methods in Washington DC Mall data set
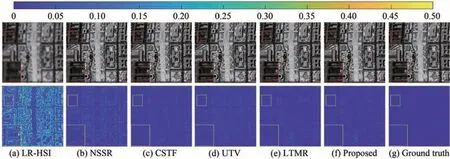
图7 第一行为Washington DC Mall 数据集第80 个波段的重构结果可视化对比,第二行为相应误差影像Fig.7 The first line gives the visual comparison of the reconstruction results at the 80th band of the Washington DC mall dataset,and the second line shows the related error image
Pavia City Center数据集的总体定量重构结果及其不同波段的PSNR 值如表5 和图6(c)所示。从表5 可知,LRTRLogTNN 在所有评价指标上仍然取得了最优值。从可视图可以看出,在Pavia City Center 数据集第63 个波段下,尽管所有方法都重构生成了较清晰的图像,但仍有部分方法产生了伪影,丢失了部分的纹理细节。如在图8 第一行中,NSSR 方法在其放大区域的屋顶显得相对模糊,而其他方法的屋顶则更接近原始图像。在第二行误差图中,可以更明显的观察到该差异,NSSR 方法重构生成的HR-HSI中充满了散乱点,LRTRLogTNN,UTV 与LTMR 方法取得的重构结果与原图更为接近。图6(c)进一步证明了该结论,尽管UTV 与LTMR 在部分波段的PSNR 值接近LRTRLogTNN,但整体数值结果明显弱于LRTRLogTNN 方法。综合上述实验结果,所提模型的整体重构表现较其他算法有明显的优势,充分证明了本文所提模型的先进性能。

表5 Pavia City Center 数据集下五个测试方法的定量评价指标结果Table 5 Quantitative evaluation index results of testing methods in Pavia City Center data set

图6 五种方法分别在三个数据集下不同波段的PSNR 值Fig.6 The PSNR values of five methods in different bands of three data sets are compared

图8 第一行为Pavia City Center 数据集第63 个波段的重构结果可视化对比,第二行为相应误差影像Fig.8 The first line gives the visualization comparison of reconstruction results at band 63 of Pavia City Center dataset,and the second line is the related error image
3.4 计算时间复杂度分析与运行时间对比

表6 展示了所提方法在Pavia City Center 数据集下与其他对比算法的运行时间比较。所有算法均在AMD R5-3600,3.6 GHZ CPU 硬件平台下运行。通过表6 可知,NSSR 方法由于仅对二维矩阵进行分解,因而运行效率最高。LTMR 方法仅对其聚类簇施加张量低秩约束,因此其运行效率仅次于NSSR 模型。CSTF 与UTV 模型均使用了张量Tucker 分解的方式,导致运行时间稍长。遗憾的是,虽然LRTRLogTNN通过子空间分解减小了HSI 的维度,但所需时间成本依然高于其他对比算法,其主要耗时在于针对每个Patch 实施非局部搜索,并计算张量环分解与张量t-SVD 运算,导致过多的非局部Patch 组以及张量运算。因此,优选非局部信息提取策略,提升模型运算效率将是本文后续重点研究工作。

表6 Pavia City Center 数据集下五个测试方法的运行时间对比结果Table 6 Comparison results of running time by applying five test methods on Pavia City Center data set
4 结论
本文研究了融合同一场景下的LR-HSI 与HR-MSI 以实现HSI 超分重构的问题,提出了一种基于LRTRLogTNN 正则项的HSI-MSI 融合方法。该模型的核心是在充分考虑光谱图像的全局谱低秩性及非局部相似先验的基础上,结合张量网络方法的优势,利用基于张量环分解的方法充分挖掘光谱图像的内在结构信息。并在此基础上,通过非凸张量秩函数近似方法更准确的逼近张量秩函数,进一步探索了因子张量的内在低秩属性,建立了低秩表达能力更强的LRTRLogTNN 正则项。多组实验结果表明,LRTRLogTNN 能有效的提高LR-HSI 的空间分辨率,得到具有近似光谱结构的HR-HSI。与现有方法相比,本文所提方法在评价指标和视觉效果上都优于目前最新的高光谱融合方法。但本文方法需要预估张量环秩,在以后的研究中,将结合自动机器学习模型以设计调整和配置该参数。

