鲁棒多特征谱聚类的高光谱影像波段选择

孙伟伟，杨刚，彭江涛，孟祥超

1.宁波大学地理与空间信息技术系,宁波315211;

2.湖北大学数学与统计学学院,湖北省应用数学重点实验室,武汉430062;

3.宁波大学信息科学与工程学院,宁波315211

1 引言

以高分五号为代表的高光谱遥感是一种先进的对地观测技术，利用较窄的光谱波段来获取地表地物的连续光谱响应信息，有利于区分具有较小光谱响应差异的地表地物（Tong 等，2014；童庆禧等，2016；Zhong 等，2018）。然而，影像的光谱维数很高且波段相关性很强，存在明显的信息冗余和计算量大问题，给数据处理和应用造成较大困难（Zhang 等，2011；张兵，2016；张良培和李家艺，2016；张良培等，2018）。波段选择能够选取代表性的波段子集，解决上述问题并最大程度地保持原始影像的应用效果（Sun 等，2015b，2016，2017a；孙伟伟等，2018）。

目前国内外学者提出多种策略来选取合适的波段子集，如排序策略、搜索策略、稀疏策略和聚类策略等（Sun 和Du，2018）。基于排序的方法通过比较每个波段的重要性来选取若干波段，如最大方差主成分分析法MVPCA（Maximum Variance Principal Component Analysis）（Chang等，1999）和限制波段选择法（Chang 和Wang，2006）。然而该方法忽略不同波段的差异性，容易选取相关性较强的波段。基于搜索的方法转换波段选择为准则函数的优化求解问题，如线性预测LP（Linear Predication）（Du 和Yang，2008）和多目标优化搜索（Pan 等，2019）。搜索策略相比排序策略能够选择更好的波段子集，然而该方法大多需要较高的计算量。基于稀疏的方法构建高光谱波段的稀疏表达模型（孙伟伟等，2017），通过求解稀疏限制的优化问题来选择代表性波段，如稀疏非负矩阵分解（Sun 等，2015a）、差异性加权稀疏表达模型（Sun 等，2016）和图正则的鲁棒主成分分析模型（Sun 和Du，2018）。稀疏系数估计对目标函数的收敛较为敏感，波段选择的结果变化较大。基于聚类的方法将所有波段聚合至不同的类别或子空间中，选择离聚类中心最近的波段，如双聚类方法（Yuan等，2016）和最优聚类框架（Wang等，2018）等。

谱聚类SC（Spectral Clustering）是一种经典的非监督聚类方法，广泛应用于高维数据的非监督聚类且效果较好（von Luxburg，2007）。谱聚类能够利用不同波段的相似性度量来构建连通图谱（或相似矩阵），实现波段在图谱上的非监督聚类并选取波段子集。采用的相似性度量如光谱角度距离SAD（Spectral Angle Distance）、相关系数CC（Correlation Coefficient）和光谱信息散度SID（Spectral Information Divergence）。近年来，随着稀疏理论引入至高光谱遥感领域，波段的稀疏系数也被用来构建相似矩阵，其中稀疏系数代表波段之间的重构概率（Sun 等，2015b，2016）。然而，上述相似性度量假设高光谱遥感成像服从高斯或线性分布，在表征波段的相似程度时，相似矩阵容易受到光谱噪声或异常值影响，从而降低波段子集的选取效果（Xia 等，2014；Sun 等，2018）。同时，上述相似性度量仅能描述波段在某一角度的相似程度，并不能够完全表征波段的全部相似特征（Sun 等，2015b）。以相关系数CC 为例，相似矩阵仅代表波段之间的相关强弱，无法体现波段之间的信息可区分性。波段选择目的是寻找信息量较大、相关性较低且差异度较高的代表性波段。因此，常规谱聚类方法构建的相似矩阵并不能够代表波段选择所需的特征信息，无法得到满足分类应用需求的波段子集。

针对上述问题，本文提出鲁棒多特征谱聚类方法RMSC（Robust Multi-feature Spectral Clustering）来改进传统SC方法，选取更优代表性的波段子集。相比传统SC 方法，RMSC 认为每一特征的相似矩阵仅能反映波段聚类的部分结构信息且受到噪声的负面影响。RMSC 通过整合单个相似特征矩阵来得到涵盖多个特征相似信息的综合相似矩阵，实现不同角度的相似信息的汇总表达，提升相似矩阵的信息总量并降低噪声的影响，改善波段子集的选取结果。假设每一特征（如信息熵、波段相关性和波段差异性）构建的波段相似矩阵具有低阶的结构特征（Xia 等，2014），RMSC 能够分解单一特征相似矩阵为综合相似矩阵和噪声矩阵，并将综合相似矩阵的估计问题转换为低秩稀疏矩阵分解问题，采用增强拉格朗日乘子ALM（Augmented Lagrangian Multiplier）（Lin 等，2015）来进行优化求解。进一步，RMSC 利用谱聚类方法来聚合所有波段至不同的类别中，从各个类别选取代表性波段。本文采用Indian Pines 和PaviaU 两个常用的高光谱影像数据集，对比5种主流的波段选择方法来验证方法的效果。

2 鲁棒多特征谱聚类的波段选择

2.1 高光谱波段的单一特征相似矩阵

假设高光谱数据的所有波段构成二维矩阵Y=[y1，…，yN]∈RM×N，其中M和N分别为像素个数和波段数量，yi为第i个波段对应的向量；选取得到的波段子集为Φ=Y(：，κ)∈RM×k，其中κ为所选波段的索引集合，k为所选的波段子集大小。考虑到波段子集的较高信息量、较低相关性和较大差异性要求，本文采用光谱信息散度SID、相关系数CC、拉普拉斯图谱LG（Laplacian Graph）（Sun 和Du，2018）和光谱角度距离SAD 来构建多个特征的相似矩阵。SID 表征不同波段的相对信息量差异，构建波段信息量特征的相似矩阵。CC 表征波段的相关性，本文利用相关系数平方和来构建描述相关性特征的相似矩阵。LG 考虑波段的内在聚类结构，利用波段的邻域结构，构建邻域差异性特征的相似矩阵。SAD 考虑波段的光谱角度差异，构建反映波段向量形状差异特性的相似矩阵。上述4个特征度量，每一个特征的相似矩阵都能够涵盖部分的波段聚类的相似性结构信息，都为非负相似矩阵。

2.2 综合相似矩阵的估计模型

假设上述4个特征的波段相似矩阵都能从某一方面来表征波段的聚类结构，RMSC 通过构建波段综合矩阵来汇总4个特征矩阵的波段相似信息，更好揭示所有波段的内在聚类结构特征。相应地，每个特征的波段相似矩阵S(i)可以分解为两部分，

式中，S(i)∈RN×N分别为光谱信息散度SID、相关系数CC、拉普拉斯图谱LG 和光谱角度距离SAD构建得到的波段相似矩阵，B∈RN×N为待求的综合相似矩阵，E(i)∈RN×N为每个特征的误差矩阵，代表其噪声或粗差的影响。约束项rank(B)=r限制矩阵B为低秩。波段的子空间聚类结构，导致位于相同子空间（或类别）的波段相似系数较大，不同类别的波段相似系数较小，从而使得矩阵B具有低秩结构。每一特征的相似矩阵都能代表大部分的波段聚类结构信息，因此限定每一相似矩阵与综合相似矩阵的差异较小。利用式（1）的低秩和稀疏分解，能够分离出单个相似矩阵的噪声信息，降低噪声影响并汇总4个特征矩阵的波段聚类结构信息。

研究表明，核范数和L1范数能够分别很好地近似表达低秩和L0范数约束条件（Sun 等，2017b）。因此，综合相似矩阵B的求解转换为一个凸优化问题：

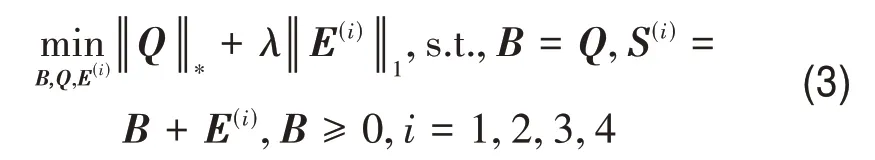
目标函数式（3）的拉格朗日方程可以展开为

式中，Λ(i)和Δ 是拉格朗日乘子，μ是惩罚参数，tr(·)是矩阵的迹。在t+1 次循环中，当固定其他变量时，变量Q的更新可以转换为

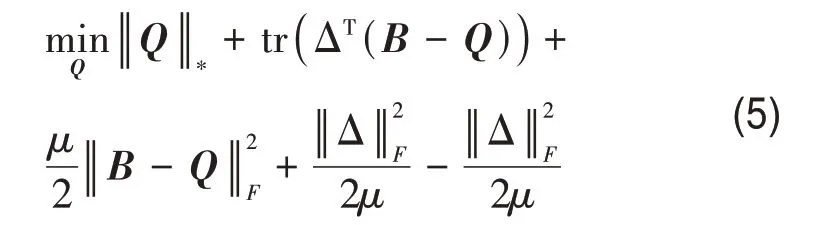
进一步，式（5）可以等价转换为

类似地，固定其他变量，求解式（8）来更新变量E(i)

接下来，固定其他变量，求解式（9）来更新变量B，

最后，固定其他变量，来依次更新拉格朗日乘子Δ(t+1)和，

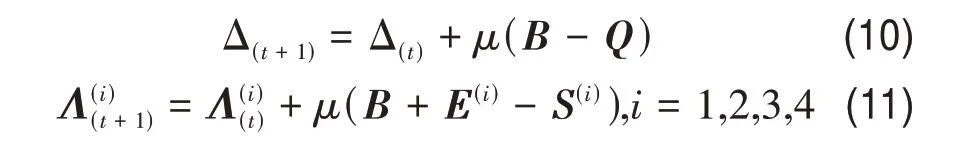
2.3 利用综合相似矩阵选取波段子集

利用优化估计的综合相似矩阵B^，采用谱聚类方法来选取最优波段子集。首先，利用B^ 来计算归一化拉普拉斯矩阵。其次，通过本征值分解来得到矩阵U，其每一列为拉普拉斯矩阵的前k个最小的非零本征值对应的本征向量。接下来，将矩阵U的每一列进行归一化处理，采用K-均值聚类方法来聚类至k个不同的类别中。最后，选择每一类中距离中心最近的行向量对应的波段来构成波段子集。RMSC选取k个波段的技术流程包括：

（1）转换高光谱影像数据立方体为二维的波段矩阵Y，利用SID，CC，SAD 和LG 度量，分别构建4个特征的波段相似矩阵；

（2）构建多特征谱聚类模型（2），将每个特征的相似矩阵分解为低秩矩阵和稀疏误差矩阵项；

（3）采用ALM算法来依次求解式（7）—（11），得到最优的波段综合相似矩阵B^；

（4）采用谱聚类方法来聚类综合相似矩阵B^，划分所有波段到k个不同的类别中；

（5）从各个聚类中寻找靠近中心最近的波段来选取得到最终的波段集Φ =Y(：，κ)。

3 实验与分析

3.1 实验数据

Indian Pines 数据由美国普渡大学的遥感应用实验室提供，于1992-06-12 通过美国JPL 成像光谱仪采集得到。影像的空间分辨率为20 m，光谱区间为200—2400 nm，预处理后的波段数为200 个。图1 为美国印第安纳州西拉法叶地区西部8 km 的一小块区域，影像大小为145×145像素，包含16类地物，其真实样本信息见表1。

图1 Indian Pines影像Fig.1 The Indian Pines image

表1 Indian Pines数据的地物真实样本信息Table 1 Ground truth of main classes on Indian Pines

PaviaU数据由自西班牙巴斯克大学智能课题组提供，由ROSIS 成像光谱仪采集得到，共103个波段，空间分辨率为1.3 m，光谱区间为430—860 nm。图2 为帕维亚大学区域的部分影像，大小为610×340像素，包含9类地物，其真实样本信息见表2。

图2 PaviaU影像Fig.2 The PaviaU image

表2 PaviaU数据的地物真实样本信息Table 2 Ground truth of main classes on PaviaU

3.2 实验分析

本节采用Indian Pines 和PaviaU 数据集，设计分类实验来验证RMSC 方法。对比的主流波段选择方法包括聚类策略方法WaluDI（Martínez-Usómartinez-Uso 等，2007）、排序策略方法快速密度峰值聚类方法FDPC（Fast Density-Peak based Clustering）（Jia 等，2016）、正交投影方法OPBS（Orthogonal Projections based Band Selection）（Zhang等，2018）和稀疏策略方法ISSC。同时，对比传统谱聚类方法SC-SID，其采用的波段相似特征性度量为光谱信息散度SID。实验分类器采用支持向量机SVM（Support Vector Machine），定量评价指标为总体分类精度OCA（Overall Classification Accuracy）。SVM 的核函数采用径向基函数，采用交叉验证方法来确定方差和惩罚因子的参数取值（https：//www.csie.ntu.edu.tw/～cjlin/libsvm/［2019-05-25］）。对每个数据集进行10 次进行独立试验，得到下述平均结果。

（1）不同波段子集大小的分类精度对比。Indian Pines 和PaviaU 数据集中波段数的选择区间为5—60，步长为5，随机选取10%作为训练样本，其余作为测试样本。Indian Pines 和PaviaU 数据集中，ISSC 的正则化因子分别取值为0.1 和0.001；RMSC的正则化因子分别取值为0.005和0.001。

图4 可以看出，OPBS 的OCA 曲线低于其他方法。RMSC 的OCA 在6 种方法中表现最优，高于SC-SID，这表明综合相似矩阵相比单一相似矩阵用于选择波段子集的显著优势。RMSC 的OCA 略高于ISSC。这是因为RMSC 采用综合相似矩阵，降低噪声负面影响并提升波段相似矩阵的信息量，从而提升波段选取效果。图3 和图5 为各种方法在波段数量为30 时得到的分类结果图。RMSC 波段子集的分类精度高于其他5 种方法，与图4 的结果保持一致。因此，在不同波段数量的条件下，RMSC的总体分类精度OCA表现最优。

图3 不同方法在Indian Pines数据的SVM分类图Fig.3 Different classification maps of Indian Pines

图4 不同波段子集下的各种方法的OCA曲线对比Fig.4 The comparison of different OCA curves with different number of selected bands

图5 不同方法在PaviaU数据的SVM分类图Fig.5 Different classification maps of PaviaU

（2）不同训练样本大小下的分类结果对比。实验中的采样比率区间为［0.05，0.1，0.15，0.2，0.25，0.3，0.35，0.4，0.45，0.5］，波段子集大小k都设置为30。图6 为RMSC 和其他几种方法的总体分类精度OCA 曲线图，总体结果与上述实验保持一致。随着训练样本的采样百分比增加，各种方法的总体分类精度OCA 逐渐提升。OPBS的OCA最低；FDPC 和WaluDI 的OCA 曲线高于OPBS，但明显低于ISSC、SC-SID 和RMSC。RMSC 的OCA在所有方法中表现最优，优于SC-SID和ISSC。

图6 不同训练样本大小下的各种波段选择方法的OCA曲线Fig.6 OCA curves of different methods with different size of training samples per class

（3）不同方法的计算效率对比。表3为不同波段子集大小条件下各种方法的计算时间，两个数据的波段子集大小的取值范围均为10—50。实验的计算平台为戴尔Win10台式计算机，硬件配置为Inter Xeon Gold 6130 CPU 2.10 GHz 和64 GB 内存，代码的执行环境为MATLAB 2014a。各种方法的计算时间随着波段数量增加逐渐上升。结合实验（1）和（2），可以看出，OPBS 方法的波段选择效果较差，但计算速度较快。WaluDI 的计算效率最低，选取的波段子集却优于FDPC 和OPBS。FDPC 和OPBS 的计算效率相比最高，但选取的波段子集结果较差。ISSC、SC-SID 和RMSC 的计算效率较高，尤其ISSC 和SC-SID，但RMSC 波段子集的分类精度最高。

表3 不同波段选择方法的计算时间对比Table 3 Lists of computational time from different methods on two datasets

（4）参数λ对RMSC 波段子集的影响分析。实验中，Indian Pines和PaviaU 数据的波段子集大小k设置为30，参数λ的选择区间为［0.001，0.005，0.01，0.05，0.1，0.5，1，5，10］。表4 列出Indian Pines 和PaviaU 数据中不同λ对应的总体分类精度OCA。可以看出，随着λ的逐渐增加，RMSC 波段子集的OCA 呈现波动但总体较为稳定。因此，参数λ的选择对RMSC 的影响有限，可以选择较小的λ来确保波段子集的较高分类精度。

表4 不同正则化参数λ下的RMSC总体分类精度Table 4 The OCA of RMSC with different choices of regularized parameter λ

4 结论

本文提出鲁棒多特征谱聚类RMSC模型来克服传统谱聚类方法中相似特征矩阵的不足，提升传统SC 用于高光谱波段选择的相似特征信息量，改善波段选择结果。RMSC 认为波段选择的目的为选取信息量大、相关性低且差异性强的波段子集。该方法整合光谱信息散度、相关系数、光谱角度距离和拉普拉斯图谱4个度量项的相似矩阵，转换波段综合相似矩阵的求解问题为单一相似矩阵的稀疏低秩分解模型；利用ALM 方法来优化求解目标函数，采用谱聚类方法来选取最佳波段子集。基于Indian Pines 和PaviaU 数据来设计4 组实验，验证RMSC方法的效果。实验结果表明，在不同的波段子集大小和不同地物的训练样本采样比例条件下，RMSC 波段子集的OCA 明显优于其他5 种主流方法WaluDI、FDPC、OPBS、ISSC 和SC-SID，而且计算效率较高。同时，正则化参数λ对RMSC波段子集的分类效果影响较小，较小的λ能够带来较高分类精度。后续工作将对比更多的波段选择方法，采用更多的数据集包括国产GF-5 卫星高光谱影像来进一步验证本文提出的方法。