数据驱动的定量遥感研究进展与挑战

杨倩倩，靳才溢，李同文，袁强强，沈焕锋，张良培

1.武汉大学测绘学院,武汉430079;

2.中山大学测绘科学与技术学院,珠海519082;

3.武汉大学资源与环境科学学院,武汉430079;

4.武汉大学测绘遥感信息工程国家重点实验室,武汉430079

1 引言

遥感卫星可以对地球表面进行大范围、持续的观测，为国家宏观决策、资源调查、灾害监测等提供及时、有效的数据支撑（徐冠华，1997）。遥感卫星获取的原始数据主要是电磁波信号，需要经过一系列的转换才能变成易理解、可应用的地表参量信息，这个转换过程被称为定量遥感。具体来说，定量遥感是利用遥感传感器获取的地表地物的电磁波信息，在先验知识和计算机系统支持下，定量获取观测目标参量或特性的方法与技术（李小文，2005）。随着遥感科学的不断发展，越来越多的卫星被发射升空，可获取的卫星数据类型变得复杂多样，数量也急剧增加，为定量遥感提出了新的挑战（宫鹏，2009；梁顺林等，2013，2016）。

作为新兴的遥感信息获取与分析方法，定量遥感强调通过数学的或物理的模型将遥感信息与观测地表目标参量联系起来，定量地反演或推算出某些地学目标参量（李小文，2005）。经典基于物理的定量遥感参数反演建模，依赖于对遥感系统机理、辐射传输理论、地表参量光学、几何等特征的理解（图1）。例如，在植被领域，Jacquemoud和Baret（1990）根据叶片内部辐射传输机制，建立了叶片的反射率/透过率估算模型PROSPECT；而后，Gastellu-Etchegorry 等（1996）基于三维辐射传输理论，建立了植被冠层模拟模型DART，实现了利用数学模型从遥感信号中提取植被信息的目的；近年来，Van der Tol等（2009）结合辐射传输和能量守恒，发展出了用于日光诱导叶绿素荧光模拟的SCOPE 模型。在水文领域，以地表能量平衡为基础的蒸散发估算模型Penman-Monteith（Monteith，1965）和Priestley-Taylor公式（Priestley和Taylor，1972），以及考虑积雪几何结构及微波辐射传输理论的雪参数计算模型Bicontinuous（Zhu等，2018），都得到了广泛的应用。大气领域，根据光谱吸收特征发展而来的差分吸收技术（陈良富等，2015）是目前痕量气体反演的主流方法；Koelemeijer等（2006）基于气溶胶基本物理属性构建的从遥感气溶胶光学厚度AOD（Aerosol Optical Depth）估算大气颗粒物质量浓度的理论公式，奠定了模型驱动的大气颗粒物浓度遥感反演的物理基础。这些方法有一个共同的特点，即都是从物理规律出发，构建从观测数据到目标参量之间的表达式，称之为模型驱动的方法。这类方法的优点是，观测数据和目标参量之间具有明确的因果关系，模型建立过程透明，可解释。但是，物理建模的方式难以准确地描述复杂多变的现实情况，一个精确、逼真的模型往往又十分复杂，计算成本高昂。除此之外，物理模型包含大量变量，这些变量难以获取和计算，也会给建模带来巨大的不确定性。

图1 模型驱动和数据驱动的定量遥感原理示意图Fig.1 Schematic diagram of the principles of model-driven and data-driven quantitative remote sensing

近年来，随着人工智能技术的发展和大数据时代的到来，数据驱动的定量反演方法开始飞速发展。如图2所示，这类方法从初始的数据或观测值出发，利用机器学习等工具寻找和建立内部特征之间的关系，从而实现时空预测或发现物理规律。得益于计算能力和人工智能算法的飞速发展，基于数据驱动的定量遥感反演方法在效率、精度等多方面都取得了卓越的成就，越来越广泛地被应用于植被、水文、冰冻圈、大气、地质等多个领域（陈仲新等，2016；李德仁等，2014b；Yuan等，2020；张兵，2018；Reichstein 等，2019；Tuia 等，2021）。然而，数据驱动的方法重在数据挖掘，忽视物理规律，因此，往往无法解释因果关系。这种机理的不透明性、因果的不可解释性也使得其受到了一定的争议和质疑。

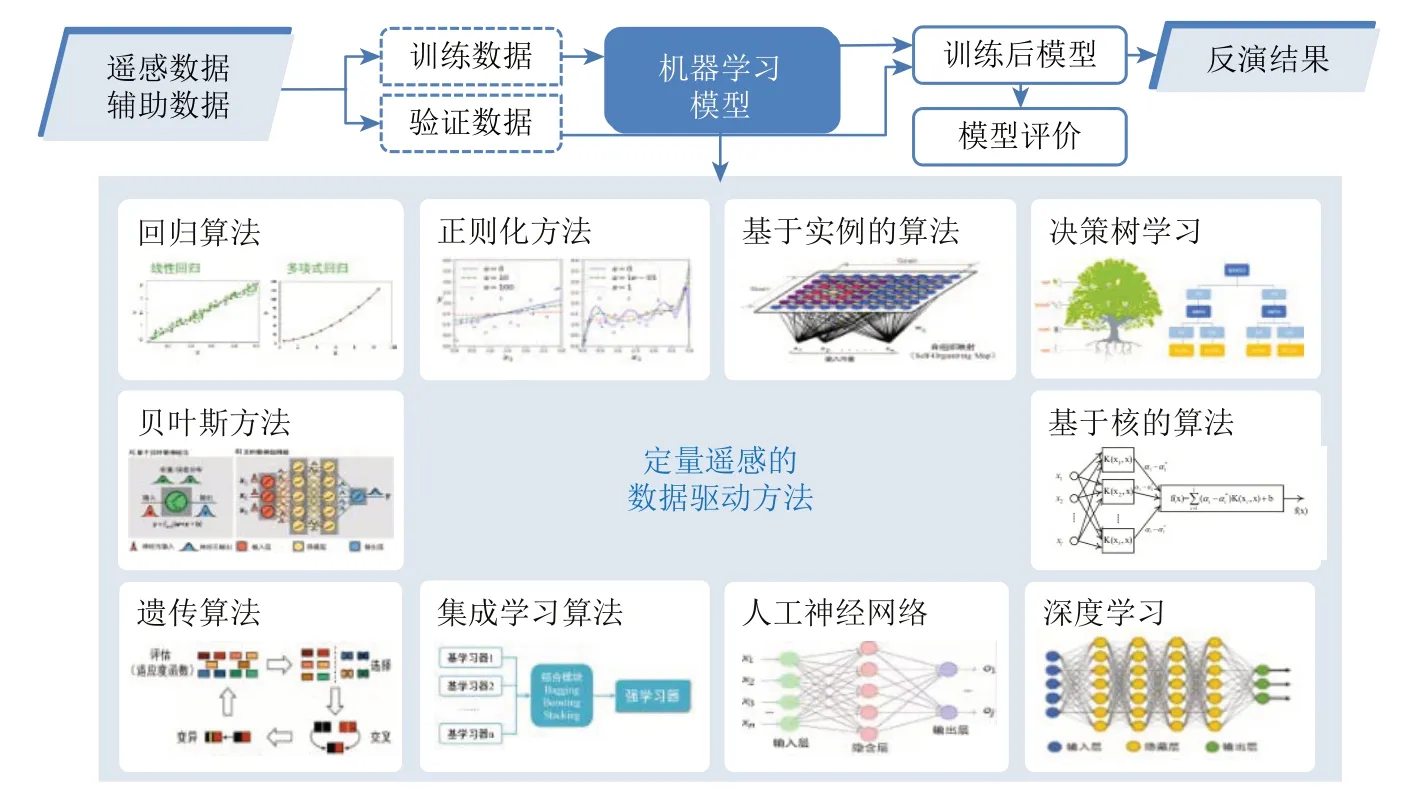
图2 定量遥感数据驱动方法流程示意图及方法分类概述Fig.2 Flowchart and classification of data-driven

模型驱动和数据驱动的方法优势互补，思考如何将二者结合，进一步提升定量遥感反演的精度，将是我们所面临的新一轮挑战。本文试图针对数据驱动的定量遥感方法进行概括，对现有的数据和模型驱动相结合的方法进行了总结，并梳理了目前我们所面临的挑战和一些潜在的发展方向。

2 数据驱动的定量遥感主流方法

本文列举了数据驱动的定量遥感反演中常用的机器学习算法，并根据算法的功能和形式的类似性，把算法进行了简单的分类（图2）。针对每一类机器学习算法，首先简单介绍其原理，阐述其在定量遥感中典型的应用实例，最后总结了该类方法的用于定量反演的优缺点（表1）。

表1 数据驱动的定量遥感方法原理及特点总结Table 1 A summary of the principles and characteristics of data-driven quantitative remote sensing retrieval methods

2.1 回归算法

定量遥感领域一种常用的较为简单的回归算法是线性回归（Linear Regression）。线性回归通过构建卫星观测和目标参量之间的线性关系，求解损失函数最小时的参数（Uyanık 和Güler，2013），实现由卫星观测到目标参量之间的反演。因建模快速简单的特点，线性回归在早期被广泛应用于各个领域（Wang和Christopher，2003；Hyyppä等，2000；Tai 等，2010）。例如Wang 和Christopher（2003）构建MODIS AOD 产品与PM2.5之间的线性关系，用于PM2.5浓度的反演；Tai 等（2010）在此基础上进一步引入气象要素，构建了多元线性回归模型；Hyyppä 等（2000）同样利用多元线性回归模型，从Landsat TM，Spot PAN 和XS 等卫星数据中反演得到了林分属性。除此之外，标准线性回归也在被不断的优化和改进，衍生出了诸多特点各异的线性回归算法。例如考虑到目标参量和卫星观测数据之间的关系会随着时间和空间而改变，学者们进一步引入考虑了时空异质性的线性混合效应模型（Lee 等，2011）和时空地理加权回归模型（Guo 等，2017；Qin 等，2017）以提升定量反演精度。

但线性回归方法不太适合处理具有非线性关系的数据，多项式回归（Polynomial Regression）（Edwards 和Parry，1993）则解决了这个问题。多项式回归的最佳拟合线不是一条直线，而是一条符合数据点的曲线，且一些自变量的指数是大于1的。相较于线性回归，多项式回归总体上更灵活，可以模拟一些复杂的关系。Cannizzaro 和Carder（2006）利用三次多项式函数拟合不同波段反射率比值与叶绿素a 浓度之间的关系，实现叶绿素a 浓度的遥感估算；Sawaya 等（2003）利用二次多项式拟合不透水表面面积百分比和IKONOS NDVI 之间的关系，实现了从NDVI 到不透水面的反演；Wang 等（2013）同样利用三次多项式，从窄波段植被水分和干物质指数比值反演得到了燃料水分含量。

在进行回归预测时，如果变量较多，往往要进行变量选择，得到最优的模型输入，因此，有学者提出了逐步式回归（Stepwise Regression）的策略。其基本思想是将变量逐个引入，引入条件是其偏回归平方和经检验后是显著的。同时，每引入一个新变量后，对已入选回归模型的老变量逐个进行检验，将经检验认为不显著的变量删除，重复此过程直至不能引入新变量，这时回归模型中解释变量集为最优。因其对输入变量的选择和控制，逐步式回归往往比非逐步式的方法可以取得更优的结果，Chen 等（2018）利用Landsat TM数据对灌木生物量估算的实验也证明了此观点。然而，Grossman 等（1996）在其用叶片反射率数据反演叶片生化信息的实验中发现，虽然逐步式回归可以得到最优的解释变量集，但是其选择出的波段与真实的吸收光谱并不相符，而且具有较大的随机性，选出的最佳波段会随着数据集、因变量类型的变化而变化。因此，作者呼吁，在鲜叶反射光谱问题上，应当谨慎的使用逐步式回归。

多元自适应回归样条MARS（Multivariate Adaptive Regression Splines）是逐步式回归的进一步推广，由美国的统计学家Friedman（1991）年提出。MARS是一种基于分段策略的非线性非参数回归方法，该方法以样条函数的张量积作为基函数，分为前向过程、后向剪枝过程两个步骤。其优势在于能够处理数据量大、维度高的数据，而且计算快捷、模型精确，可解释性强。在Kuter 等（2018）利用MODIS数据反演积雪覆盖比的实验中，MARS取得了和神经网络算法相媲美的精度，与此同时，MARS 的计算效率远高于神经网络算法。Huang 等（2020）利用MARS 进行河流组分浓度等反演，并基于MARS算法良好的可解释性，详细讨论了自变量和因变量之间的交互作用。Islam 等（2015）利用MARS和微波遥感数据进行降雨率的反演，并认为MARS具有高效、灵活的特点，将十分适用于全球降雨数据的反演。在地上生物量定量反演的实验中，作者利用高光谱数据及其他辅助变量作为输入，结果表明，MARS在高维数据下也可以取得较好的反演结果（Filippi等，2014）。

2.2 正则化方法

正则化方法一般指向模型中引入附加约束以防止过拟合和提升模型性能的一类方法（Bickel等，2006）。例如，为了解决标准线性和多项式回归在特征变量共线性的情况下会失败的问题，发展出了岭回归（Ridge Regression）（Hoerl 和Kennard，1970）和Lasso 回归（Least Absolute Shrinkage and Selection Operator）（Kukreja 等，2006），以及弹性网络（Elastic Net）（Zou 和Hastie，2005）。它们都是在回归优化函数中增加一个偏置项，以减少共线性的影响，从而减少模型方差。区别在于岭回归使用L2 正则化，Lasso 回归使用L1 正则化，而弹性网络ElasticNet 同时使用L1 和L2 正则化。这些正则化方法在输入变量具有高维度和多重共线性的情况下也能有良好的效果Kang 等（2018）利用这一特性，通过引入岭回归，解决了土壤湿度站点之间的共线性问题，实现了对稀疏土壤湿度观测的空间升尺度。除此之外，正则化作为一种灵活的约束方法，可以以不同的形式与多种不同的模型相结合。有许多学者根据待解决问题的特点，将一些先验知识作为正则化项加入到机器学习算法中，以提升模型性能。例如，Atzberger（2004）和Combal等（2003）将辐射信息作为正则化所需的先验信息，提升了基于人工神经网络的冠层参数反演模型的性能。Hang 等（2017）提出图正则化非线性岭回归算法（KGRR），并应用于高光谱分类和气溶胶反演任务。结果表明，相比于普通的岭回归算法，支持向量机，以及神经网络算法，KGRR在分类和回归任务中均具有更优的表现。未来，这种根据特定问题改进的机器学习算法，以及多类算法融合的模式，将成为学者们重点关注的方向之一。

2.3 基于实例的算法

不同于大多数机器学习算法都有围绕目标函数建立起来的明确的一般化描述，基于实例的算法（Instance-based learning）直接通过存储的数据集进行分类或回归来得到学习结果。代表性算法包括K 邻近算法（KNN），自组织映射算法SOM（Self-Organizing Map），局部加权回归等。定量遥感领域的应用包括利用K 邻近回归（KNR）进行叶面积指数（Wei 等，2017）、生物量（Antropov等，2017）的反演；利用SOM 算法实现二次浮游植物色素（El Hourany等，2019）、叶绿素a垂直分布（Charantonis等，2015）的估算，以及总悬浮颗粒物浓度产品的评估（Gao 等，2019）等。但基于实例的算法内存使用往往较高、计算成本高，无法用于高维特征空间，因此应用也较为受限。

2.4 决策树学习

决策树算法根据数据的属性采用树状结构建立模型，常见的算法包括：ID3（IterativeDichotomiser 3），CART（Classification And Regression Tree），以及C4.5。由于单棵决策树的学习能力有限（不如决策树的集成算法如随机森林），因此在定量遥感领域的应用较为有限，主要包括用于植被类型、土壤类型、积雪判别等分类问题（Elnaggar 和Noller，2009；Ghulam 等，2014；Grody 和Basist，1996），以及少量的回归反演任务中（Caicedo 等，2014；Jiang等，2021）。

2.5 贝叶斯方法

贝叶斯方法算法是基于贝叶斯定理的一类算法，常见的包括：朴素贝叶斯算法，平均单依赖估计AODE（Averaged One-Dependence Estimators），以及贝叶斯（信念）网络BBN（Bayesian Belief Network）。前两者主要用于分类问题，因此在定量遥感反演中应用较少。而贝叶斯网络则应用较多，尤其是在植被参数定量反演遥感问题上（Qu 等，2008；Xu 等，2019；Zhang 等，2012），其基本原理是利用叶面积指数、叶绿素浓度、光谱反射率、卫星观测角等参数，构建一个有向无环图，利用该概率图模型，结合贝叶斯理论，完成对植被参数的定量反演。由于贝叶斯模型可以在一定程度上反应变量之间的因果关系，并根据已有的知识做出推断，近年来，其与深度学习模型的结合也成为了一大研究热点，贝叶斯神经网络BNN（Bayesian Neural Network）也因此诞生。其核心思想是将神经网络中的权重看作某种分布，而非固定值。由于其预测值也是概率分布，因此，BNN 可以度量预测结果的不确定性。Ma 等（2021）利用BNN，结合MODIS 数据，气候数据和土壤属性数据，实现了对玉米产量的预测，并对预测值的不确定性进行了评估。BNN 不仅能够评估预测结果的不确定性，也能够在小样本情况下取得很好的效果（Ma 等，2021），然而，目前基于BNN 进行参数定量反演的工作还相对较少，值得进步一步探索和挖掘。

2.6 基于核的算法

基于核的算法把输入的原始空间的特征映射到高维甚至无穷维空间中，并在高维空间学习得到对应的线性模型，使模型具有极强的非线性表达能力。其中最著名的当属支持向量机SVM（Support Vector Machine）。SVM 最初主要被用于分类任务，后来Vapnik 等（1996）发展出了用于回归的SVM算法，称为支持向量回归（SVR）。SVM 算法适合小数量样本数据；算法设计很好的避免了维度灾难，可以解决高维问题；不但简单，而且具有较好的鲁棒性和泛化性。因此，20世纪以来，深入地球和遥感科学的各个领域，得到颇为广泛的应用。其他基于核的算法也包括相关向量机（RVM），核岭回归（KRR）等，也已被应用于陆地、海洋和大气等多个领域（Camps-Valls 和Bruzzone，2009；Verrelst等，2015）。Camps-Valls和Bruzzone（2009）在其专著中对基于核的算法在遥感领域中的应用做出了系统的总结，认为基于核的算法已经成为了遥感应用领域的标准方法之一。Mountrakis 等2011）在其综述论文中对SVM 算法在遥感中的应用，以及SVM 算法的优缺点做出了总结。作者指出，虽然SVM算法优势众多，但其依然存在参数敏感、噪声敏感，难以用于大规模样本训练的问题。因此，在地球大数据时代（李德仁等，2014a），面对海量的待处理数据，SVM 算法也存在一定的局限性，需要进一步的改进和提升（Foody，2008）。

2.7 遗传算法

遗传算法是一种基于达尔文进化论的全局寻优算法，最早由Holland 在1969年提出，后经多位学者整理形成（De Jong，1975；Goldberg和Holland 1988；Holland，1975）。遗传算法首先通过编码将待求解的问题表示成遗传空间的染色体或者个体，令个体之间进行交叉和变异；同时根据所求问题的目标函数来设计适应度函数，使得算法不断对编码后的参数进行搜索寻优，直到找到最优解或达到最大进化代数。遗传算法适用于非常复杂和困难的环境，比如，带有大量噪声和无关数据、事物不断更新、问题目标不能明显和精确地定义等；且具有较好的鲁棒性。在定量遥感领域，遗传算法也被用于土地利用分类（Tseng 等，2008）和冰云属性反演（Liu 等，2021）等问题。除此之外，作为一种全局优化算法，遗传算法也能很好的与其他算法相融合。例如，与偏最小二乘算法耦合（GA-PLS），从遥感反射率数据反演植被等效水厚度和鲜叶片燃料水分含量（Li 等，2008，2007）；与极值梯度提升树耦合（XGBR-GA）（Pham 等，2020），利用多源遥感数据反演得到地上生物量，并且取得了比梯度提升树、支持向量机、随机森林更好的精度；以及与神经网络算法耦合（GA-BP），协同主被动微波遥感，反演土壤水分。作者认为，遗传算法很好地弥补了神经网络容易陷入局部最小的缺点，且使神经网络具有较快的收敛性、全局优化的能力和较强的学习能力（余凡等，2012）。

2.8 集成算法

上述算法主要都是单个学习器，他们在性能提升上往往存在一定的瓶颈，也可能容易出现过拟合或欠拟合的问题；因此，集成多个学习器来提高模型性能的方法应运而生，这就是集成学习算法（Ensemble Learning）。集成算法根据集成方式的不同一般分为3 类：（1）Bagging。以并行的方式把弱学习器的结果组织起来，通过投票或取平均等折中的方式取得最终的结果，代表性算法为随机森林（Random Forest）。（2）Boosting。以串联的方式组织模型，根据旧模型中的错误来训练新模型，层层改进，代表性算法为AdaBoost、梯度提升决策树GBDT（Gradient Boosting Decision Tree）。（3）Stacking。使用上一阶段的预测结果作为下一层预测的输入特征，重新训练一个新的学习器，输出最终的结果。代表性算法为堆叠泛化（Stacked Generalization）。集成算法的泛化能力和预测性能通常比单个学习者更强大，因此应用十分广泛。从陆地遥感，到海洋遥感，到大气遥感，无论是分类问题，还是定量反演问题，集成学习等法，都得到了广泛的应用。（Healey 等，2018；Lee 等，2019；Wang 等，2019）。集成算法优越的性能使得它成为了机器学习领域重要的发展方向之一，其在定量遥感领域的应用潜力也有进一步挖掘的价值，值得重点关注。

2.9 人工神经网络

作为过去十年中最具影响力的技术之一，人工神经网络收到了空前广泛的关注。人工智能先驱的最初愿景是复制人类大脑的功能，人工神经网络便是模拟生物神经网络的产物。它由输入层，隐藏层和输出层组成，其中输入层从外部接收数据，一个或多个隐藏层处理数据，输出层提供一个或多个神经元输出结果。人工神经网络是机器学习的一个庞大的分支，有几百种不同的算法，深度学习就属于其中之一，将在下节具体讨论，因此，本节的神经网络算法主要指非深度学习的浅层网络。神经网络算法十分灵活，可以快速调整，适应各种不同类型的新问题，因此，同集成算法一样，应用十分之广泛。其在定量遥感领域的应用，可以追溯到20世纪90年代，最初主要被用于遥感影像分类问题（Parikh 等，1990），不久后也被引入定量反演问题中（Davis等，1993）。其中，最为常用的是具有多层感知器结构的反向传播神经网络BPNN（Back Propagation Neural Network）（Dong 等，2020；Tedesco 等，2004）。除此之外，自组织映射（Chang 和Islam，2000）、广义回归神经网络（Li 等，2017）等也有一定的应用。神经网络具有高度的灵活性，近几年，根据特定的问题而设计特定的神经网络，受到了诸多学者的关注。Li 等（2020a）将时空异质性融入广义回归神经网络，提出了时空加权神经网络，充分考虑了PM2.5浓度和AOD 关系的时空差异，提升了传统广义回归神经网络的效果。Wu 等（2021）将这种时空加权策略和时空邻近神经网络相融合，提出的时空神经网络加权回归算法，同样取得了比传统算法更优异的表现。这种考虑待解问题特性的而设计的神经网络，将是一个重要的发展方向之一。

2.10 深度学习

深度学习算法是对人工神经网络的进一步发展。近年来，随着计算能力的不断提升，深度学习迎来了飞速的发展，网络结构日趋复杂。深度学习在定量遥感领域的起步不久，却已经取得了突出的成就，受到了广泛的关注。深度神经网络DNN（Deep Neural Network）（Su 等，2020），深度信念网络DBN（Deep Belief Networks）（Shen 等，2018），卷积网络CNN（Convolutional Neural Network）（Malmgren-Hansen 等，2019），长短期记忆神经网络LSTM（Long Short-Term Memory）（Ma等，2019）、图神经网络GNN（Graph Neural Netwoek）均得到了应用和发展。Yuan 等（2020）对遥感领域常用的深度学习模型结构，深度学习在环境遥感中的具体应用，以及目前面临的挑战和可能的发展方向，做出了系统的总结：相比于深度学习算法的发展速度，深度学习在定量遥感领域的应用还有待深入，迁移学习、生成对抗学习、小样本学习、耦合物理规律的深度学习等问题仍有待探索。

3 数据驱动和模型驱动的结合

基于数据及归纳的人工智能方法（机器学习，Machine Learning）可以从不断增长的地理空间数据流中捕捉信息、提取模式（Reichstein 等，2019），有很强的数据适应性，但同时，机器学习缺乏理论支持、可解释性弱等“黑匣子”问题亟待解决。因此，传统的物理模型的发展也不容忽视。不同于机器学习，理论模型基于知识及演绎，包含丰富的底层系统知识，其结果可解释性强（Boukabara 等，2021）。在地球科学系统中，两者虽驱动力不同，却具有相同目的，即通过数据分析或数学建模来预测行为（Dueben 和Bauer，2018）。故在大数据背景下，数据驱动方法和模型驱动方法的优势结合成为定量遥感各研究领域的热点。

基于不同的主体，两者结合的相关工作可大致分为两组：机器学习辅助的模型模拟和模型辅助的机器学习。前者利用机器学习优化理论模型，进行集成建模；后者将先验知识整合到机器学习中，可描述为知情机器学习（von Rueden等，2020）。

3.1 机器学习辅助的模型模拟

模型模拟是一种自上而下的模型驱动方法，具有坚实的理论框架。从系统的角度出发，机器学习可从原始系统、子模型、参数3个层次对其进行优化（图3）。如图3所示，优化系统为利用机器学习方法纠正数据同化过程中可能存在的系统误差；优化子模型为训练XGBoost模型替代大气化学传输模型中的化学积分过程（Keller 和Evans，2019），以提高效率；优化参数为基于神经网络模拟气溶胶物理参数VEf和相关变量的函数关系，从而优化PMRS大气物理模型（Zhang和Li，2015）。

3.1.1 优化系统：校正系统偏差

假设没有观测偏差，模型模拟与观测值的偏差可归因于不完善的知识而产生的系统误差。机器学习能有效识别、提取并可视化模型错误的模式，从而纠正相应初始动态变量的隐式系统误差（Reichstein 等，2019）。近年，Pathak 等（2018）探索了混合“数据辅助”动力学模型在预测方案中校正偏差的可能性。进一步，机器学习辅助优化有助于填补系统知识空白、探索物理方程进而改进理论模型。

数据同化（Data Assimilation）使得观测与模型协同发展，是地球科学系统中的一个重大领域（Eyre 等，2020）。它以物理模型为基础，通过融合多源观测数据进行系统状态的估计、观测—模型的不确定度评估，从而提高系统的可预测性（Li等，2020b）。Geer（2021）分析了贝叶斯框架下数据同化和机器学习的统一性，机器学习的融入为搜索数据同化中统计度量的最佳拟合提供了可行方案。例如，Irrgang 等（2020）提出了一种基于机器学习的大气强迫不确定性估计方法，其结果作为数据同化中误差协方差信息的来源；Cintra和de Campos Velho（2014）利用机器学习模拟了Kalman 滤波方案从而嵌入大气环流模式；Ruckstuhl 等（2021）训练卷积神经网络来维持数据同化中的质量守恒，从而增强了遥感数据、地面数据与模型模拟结果的一致性。

3.1.2 优化子模型：代理建模

模型模拟的大框架往往由许多子模型构成，如果子模型是半经验性质的，其函数形式理论基础较弱（例如，生物过程），代理建模可在保持能量守恒定律等物理规律的前提下，实现子模型和全模型的误差分离，从而优化建模。另外，偏微分方程求解的不确定性问题也是模型发展存在的问题之一（Zanna 等，2019）。此思路已被用于优化海水运动场，De Bezenac 等（2018）建立了卷积-反卷积神经网络以学习海水的运动场，然后使用物理模型进一步处理以更新热含量和温度。Mo等（2019）利用深卷积编解码网络替代传统的蒙特卡罗（Monte Carlo）方法量化动态多相流问题的不确定性，提升了地下水模型的预测效率（如压力和饱和度）。在大气科学领域，Keller 和Evans（2019）将机器学习如随机森林方法引入大气化学传输模式，通过替代化学积分器这一子过程简化化学微分方程的计算，提升计算速度的同时，输出的大气污染物浓度与原模式精度相当如图3中优化统环节所示。Rasp 等（2018）将神经网络用于气候模型SPCAM（Super-Parameterized Community Atmosphere Model v3.0）中的大气亚格网过程的近似，具有快速准确的优势，显示了数据驱动下气候模式开发的潜力。

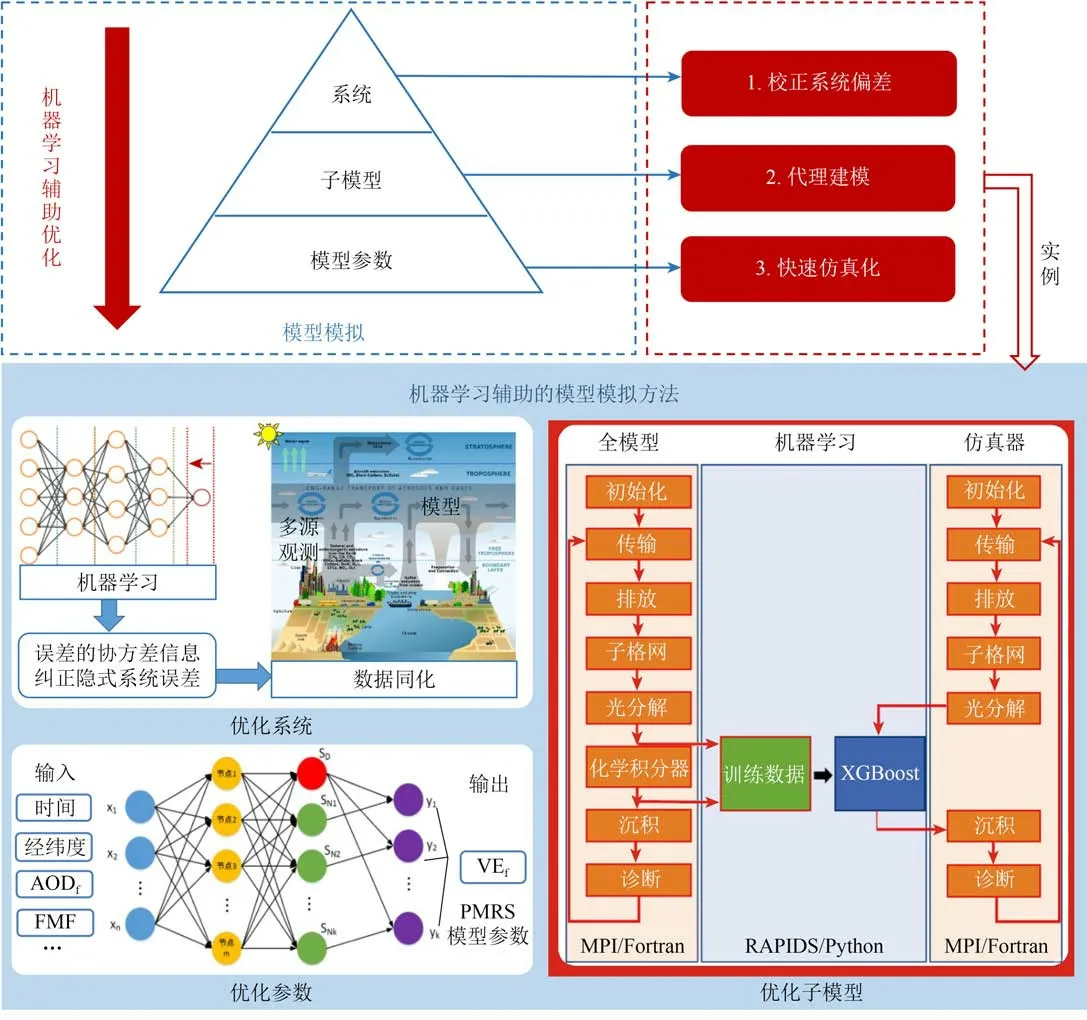
图3 机器学习辅助的模型模拟：3种优化思路Fig.3 Three optimization ideas for model simulation assisted by machine learning

3.1.3 优化参数：快速仿真化

机器学习可提供误差相对较小的模型参数的函数近似（Veerman 等，2021），实现快速仿真。针对气候模式难以表征的湿对流相关参数，Gentine等（2018）提出了一种新的基于机器学习的对流参数化方法，其从明确的模拟中学习对流的显著特征，计算效率显著高于超参数化；基于准地转海洋模式（Quasi-Geostrophic Ocean Model），Bolton 和Zanna（2019）成功利用神经网络表示涡流动量强迫的时空变异性，对动量的涡动参数化和更普遍的亚网格参数化有重要意义；目前，大气辐射参数和行星边界层的机器学习模拟也应用广泛，研究表明短波辐射计算因机器学习的参数仿真加快了约60 倍（Boukabara，2020）。Sawada（2020）结合微波亮温数据和MCMC（Markov Chain Monte Carlo）算法，使用统计机器学习的代理建模技术加速了陆地表面模型（Land Surface Model）中土地湿度和植被含水量相关的4个参数优化和不确定性评估。

此外，在实现快速仿真的同时，Yuval 和O’Gorman（2020）通过优化高分辨率模型训练数据，探索了机器学习应用于气候建模中亚网格过程的稳定参数化的可能性。对于大气领域的物理模型来说，代表气溶胶光学性质的相关物理参数对准确反演大气污染物（如PM2.5）至关重要。Zhang 和Li（2015）提出一种不依赖于地面站点数据的颗粒物反演模型PMRS（Particulate Matter Remote Sensing method），并将关键物理参数—柱状体积消光比VEf（columnar volume-to extinction ratio of fine particulates）拟合为有关细粒子分数的二次多项式。VEf包含复杂的粒子微物理性质，且与光学参数紧密联系，基于此，神经网络可建立VEf与多个相关变量之间的模型，例如遥感卫星提供的细粒子分数FMF（Fine Mode Fraction）、AOD 等。图3中优化参数环节展现了具体思路，通过捕捉上述变量、时空变量和VEf之间的复杂关系，优化该物理参数的表达，从而进一步提升PM2.5反演的精度。

3.2 模型辅助的机器学习

机器学习以数据作为驱动力，“自下而上”地刻画地球科学系统中各变量之间复杂的非线性关系。将物理模型有关的先验知识引入其中，有利于提高它的合理性及可解释性。从机器学习训练的角度出发，模式可从数据、过程、结果等3个方面对其进行增强（图4）。

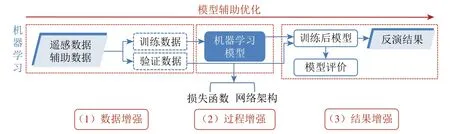
图4 模型辅助的机器学习的3种优化思路Fig.4 Three optimization ideas for model-assisted machine learning

3.2.1 数据增强

现实观测数据（例如遥感数据、地面数据等）通常具有非平稳性，而模型却没有直接的观测限制（van Donkelaar 等，2015）。将模型模拟数据作为机器学习的附加数据来源，数据集得以扩展，物理性知识融入训练过程，数据质量得以增强。

在大气污染物浓度反演过程中，化学传输模型CTM（Chemical Transport Model）可提供关于历史污染物浓度额外有价值的信息。例如，将CTM的模拟PM2.5值或PM2.5组分信息纳入总数据集，与卫星AOD 数据、气象变量等一同建模，其为PM2.5的时空变化提供了先验知识（LYU 等，2019）。为结合观测和多模型输出，Chang 等（2019）探索了一种新的方法（M3Fusion v1）以改进全球表面臭氧分布估计，进一步可利用机器学习优化。在水文领域，Yang 等（2020）为填充稀疏观测开发了物理过程和神经网络组合的水文模型，其在有限的观测数据下能模拟大流域的日流量，并探究了合成数据驱动的机器学习模型的性能优越性；Yin等（2021）融入地表水流系统输出，用贝叶斯机器学习集成方法较好地预测了地下水蓄水量变化。另外，Berger等（2020）通过耦合叶片光学特性模型PROSPECT-PRO 与冠层反射率模型4SAIL 生成了一个训练数据库，基于概率机器学习回归方法，提出了一种估计农作物氮含量的混合反演方法。目前高光谱及多光谱图像是遥感监测氮含量的主要数据来源，所建立的模型具有较强的泛化能力、较大的时空覆盖范围（陈永喆等，2017）。结合多源数据优势，耦合定量遥感和物理模型方法进行反演，也将成为未来研究的一大热点。

3.2.2 过程增强

目前，生成对抗网络GAN（Generative Adversarial Networks）得到迅速发展以实现将模拟集成到学习算法中的功能，例如，PI-GANs（Wu 等，2020）确保了生成样本的气候协方差与训练数据集的气候协方差相匹配。理论上，模型能引导机器学习的训练过程，给予算法相应的物理约束，基于此在不同领域也开发了不同的混合机器学习模型。具体方式主要分为以下两种。

（1）较为流行的方法是将物理约束作为损失函数的附加项，增强学习结果的物理一致性。Beucler 等（2020）使用温度—密度—深度的物理转换关系设计神经网络损失函数的一部分，基于湖泊模型模拟构建了物理引导的神经网络（PGNN）以反演水温。在此基础上，Jia等（2018）考虑LSTM 模型的时间建模结构，增加了对预测水温随时间变化的约束，使训练过程遵循能量守恒。Zhao 等（2019）将基于能量平衡、扩散理论的二次Penman-Monteith 方程方程嵌入损失函数以反演蒸发模型中的潜在热通量，实验证明该网络具有更高的泛化能力。Beucler 等（2020）以约束矩阵的形式反映对流模型中需要遵循的守恒规律，设计损失函数中的附加项并进行加权组合，相比于原始网络，对流增湿变量的预测误差显著降低。

（2）通过更改网络架构，将模型中的物理规律整合入训练过程，从而形成约束层。Jiang 等（2020a）构造了一个特殊循环神经层来包装物理模型（时间动态地球科学模型），作为深度学习架构中一部分进行训练，输出动态响应（如每日的径流量），中间变量例如积雪蓄水量也得到较高精度的模拟。同时，Beucler等（2020）探究了ACnet网络以预测对流增湿和增热变量，平衡了模型精度和物理一致性，网络把质量、能量、辐射守恒定律整合于约束层以输出额外的变量值，计算残差从而协同优化网络。为预测云过程（即对流和辐射）对气候影响的多维向量。Beucler 等（2019）在构建网络时纳入4种守恒定律，同时提出设计损失函数和更改网络架构两种方法，前者合理选择物理附加项的加权值，后者通过求解约束方程组计算输出向量的4个分量，结果表明物理约束信息可以显著提高模型泛化能力。此优化思路同样可应用于其他领域，通过变换与各反演变量相关的物理模型的表达形式，将其合理嵌入神经网络以实现反演，理论上遥感模型的精度及普适性将得到进一步提升。

上述模型辅助机器学习的过程增强使得整个任务序列是通过统一的人工智能架构完成，从结构上弥补了机器学习的物理不一致问题。此外，基于深度学习的灵活性和易于扩展性，常规神经网络层也可置于物理约束层之上以提供输入，例如云的参数化（Rasp等，2018），Jiang等（2020b）对网络施加一组偏微分方程约束，搭建了一个时空超分辨率框架以从低分辨率输入中生成高分辨率时空解，此研究对于定量遥感也具有一定意义。

3.2.3 结果增强

神经网络中的性能度量可用两种方法来表示，一种是损失函数，另一种是辅助度量，后者通过定义和跟踪一个或多个额外的期望性能标准（不必可微），在每次网络训练后对其进行评估，以确保立即检测到不可接受的权衡（Ebert-Uphoff 和Hilburn，2020）。为了充分挖掘降水的潜在降尺度解，Chen 等（2020）设计了一个学习降水图的隐式物理运动估计框架（RainNet）并将8 个基于数据集物理性质的度量标准纳入评价标准。从这个角度看，模型约束可作为机器学习的结果增强手段。

其次，可从网络解空间的角度出发进行增强。Kraft 等（2020）提出了一个端到端的全球混合水文模型，其目的为反演总蓄水量、径流量、蒸散量以及雪水当量。模型将概念性水平衡模型机理融入动态神经网络的解空间，使相关变量保持可解释性。从深度学习的角度来看，混合方法可看作是神经网络的正则化，将解空间限制为物理上合理的结果。同时，复杂物理模型的大范围动力学模拟（如云分辨率模型）对神经网络结果的测试也奠定了坚实的基础（Pal等，2019）。

3.3 两者融合的问题与挑战

任何直接从数据中学习的方式都必须应对地球科学发展的挑战（Geer，2021），其中包括以定量的方式表示不确定性、建立观测数据与地学过程的联系等。在大数据时代，二者融合同样面临类似问题。

（1）物理模型内部机理的复杂性。优化模型中的某一步骤或参数，是近年来机器学习嵌入物理模型中的主流方法，故明确各领域有关参数意义至关重要。解决此问题需促进地理学、生物学、人工智能学等众多领域交叉合作，探寻与已知或未知参数相关的变量，赋予数据可解释性从而以简代繁，使机器学习有针对性地提升精度。

（2）联合模型的不确定性。将物理意义与大数据驱动思路有效结合，如何减少联合模型的不确定性是需要攻克的一大难关。例如，在带有物理约束条件的深度学习训练中，若地面测量数据与物理模型输出值同为训练真值，则需合理分配二者占比，降低网络学习中的不确定性，从而使其更好地协同优化网络。另外，定量指标是评价模型结果的重要标准，机器学习注重精度，物理模型强调地学意义，在训练模型过程如何均衡考虑两类指标以优化建模尤为关键。

（3）联合模型的泛化能力。由于样本的限制，机器学习方法在小区域内表现良好，泛化能力因数据性质及训练方法而有所差别，当适用于普遍数据的物理模型嵌入后，模型是否能在大范围内保持良好的预测能力，仍有待验证。

（4）联合模型的可迁移性。不同领域研究基于的物理模型、观测数据类型不一致，应用的人工智能方法也大相径庭，当联合模型的优良架构（如GAN）出现，是否可以在理论相近的子领域进行模型迁移，例如云辐射、气溶胶、颗粒物等大气相关研究方向，此思路则需要多个领域共同探究并深入合作。

（5）小样本情况下的联合建模问题。物理模型中的相关参数往往表征了复杂的物理特性，且与多种性质相关，故某些物理模型的中间参数难以通过观测获得，即训练真值数量较少。当样本稀疏时，需要通过合适的机器学习方法来表达、模拟及验证参数，此外，不拘泥于该替代建模步骤的样本验证，也可对后续步骤的精度提升效果做出定量评价，判断机器学习训练的模型是否可靠。

物理模型包含丰富的可解释性知识，多源数据的融入有助于改善理论、优化系统，机器学习的辅助有利于其效率、精度的提升。虽然放弃物理模型知识并从零开始使用机器学习很有诱惑力（Sønderby等，2020），但考虑模型理论并将其嵌入学习过程会从先前的知识中获益，从而优化反演结果。实现数据驱动和模型驱动方法的协调发展，使两者相互促进、相互融合，也是深入研究地球科学系统各领域问题的大势所趋。

4 结语

定量遥感可以看作是将数据转化为信息的过程。模型驱动的定量遥感通过现有认知，如物理规律、生化性质等，从数据中提炼信息，形成新的认知。是一个旧认知产生新认知，旧模型驱动新模型，从而不断完善对地球系统的认知和建模的过程。数据驱动的定量遥感则通过对数据进行“学习”来得到目标信息，它不关心现有的认知和理论框架，而关心如何“学习”。从简单的一元线性回归，到集成学习、深度学习；从单一场景、单一要素的物理建模，到考虑多场景，多要素，数据驱动和模型驱动的方法都经历了长足的发展，在不断进步和完善。然而，随着对两类模型研究的深入，他们的各自的局限性也日渐凸显，数据驱动的方法忽视内在机理，弱化因果关系；模型驱动的方法不确定性大，成本高昂。基于此，耦合物理规律和机器学习，构建模型和数据共同驱动的反演框架，成为了定量遥感领域新的研究热点。现有研究或用机器学习优化物理模型，或用物理规律增强机器学习的预测能力，均取得了一定的成效。然而，当前的耦合仍然为浅层的耦合，对复杂的物理模型内部机理挖掘尚浅，模型效果提升较为有限。除此之外，联合模型的不确定性、泛化能力、可迁移性、小样本情况下的适用性仍有待探讨。未来，探索深度耦合的新思路，新方法，将是定量遥感发展的重要方向之一。