半导体激光器速率方程的参数提取(特邀)
,黄永光,刘祎慧
(1 中国科学院半导体研究所材料重点实验室,北京100083)
(2 中国科学院大学材料与光电研究中心,北京100049)
(3 低维半导体材料与器件北京市重点实验室,北京100083)
0 引言
在模拟通讯系统中,激光器需要以较大的工作电流工作在线性区以满足微波性能需要。为描述微波性能会引入一些噪声等指标,如三阶交调(Third Order Intermodulation,IMD3)、二次谐波(Second Harmonic Distortion,HD2)、相对强度噪声(Relative Intensity Noise,RIN)等[1-3]。直接获取这些指标需要通过复杂的测试系统,不仅设备昂贵而且测试难度大,很难便捷、准确地获取所需的性能指标,这样就对半导体激光器的性能评估造成较大困难。
根据速率方程理论,半导体激光器的动态性能指标与激光器器件参数之间存在着定量关系。从速率方程中提取半导体激光器参数并对其进行量化分析有助于进一步优化提升半导体激光器的动态性能,从而对半导体激光器的设计、制作和应用提供重要理论参考。通过先将激光器的部分性能指标测试出来,再利用速率方程理论提取器件参数重新计算器件在大电流工作下的微波性能指标,可以有效降低器件测试成本、提高器件设计效率。文献常规的参数提取方法可以得到半导体激光器工作在偏置电流较低(10~40 mA)的参数值,但这种方法在大电流工作时的器件参数提取不太准确,而且需要测啁啾等更多繁杂的测试[4-7]。
本文介绍了一种利用小信号频率响应曲线精确提取半导体激光器谐振频率fr与阻尼因子γ的新方法,且对应激光器的驱动电流范围广,给出的案例驱动电流范围为20~90 mA,可满足大电流工作需要。根据激光器的功率-电流(P-I)响应特性,结合已提取的器件参数,代入速率方程可计算出激光器的各个性能参数,方法便捷、准确。
1 理论推导
在讨论半导体激光器器件设计参数与相应的器件动态指标的关系时,常采用速率方程理论。它以唯象参数为工具,建立起光子与载流子之间的相互作用关系。半导体激光器单模速率方程表达式为[8-10]

输出功率P(t)与光子密度S(t)的关系式为
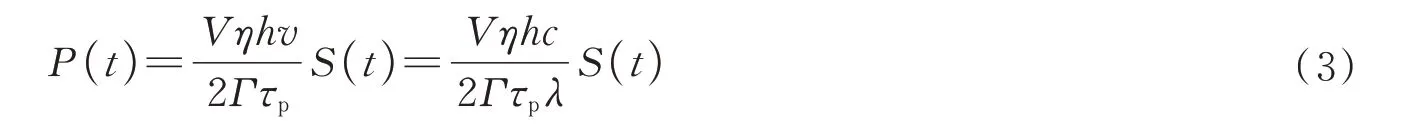
式中,N(t)为载流子密度;S(t)为光子密度;I(t)为注入电流;V为有源区体积;e为电子电荷;τn为载流子寿命;g0为光增益系数;ε为增益压缩因子;N0为透明载流子密度;Γ为限制因子;τp为光子寿命;β为自发发射因子;P(t)为输出光功率;η为微分量子效率;h为普朗克常量;v为光频率;c为光速;λ为波长。
当半导体激光器工作在直流稳态的情况下,载流子密度和光子密度达到稳定状态,这时有

结合式(1)~(3),并利用直流稳态工作条件式(4)进行推导变换可得
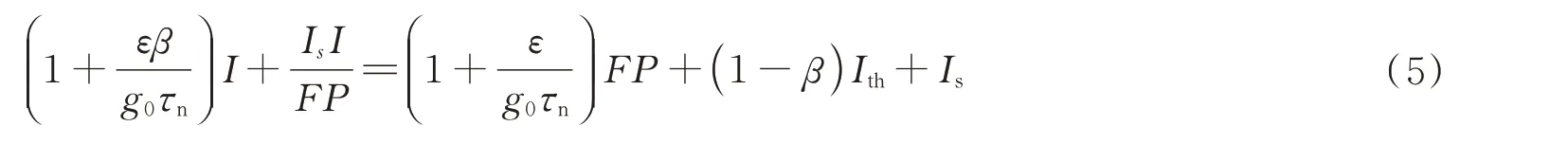
式中,Ith为阈值电流,IS为自发发射因子,F为中间变量,具体的变量值为

当激光器工作在阈值附近时光子密度很低,εS很小可以忽略[7,11-12],因此式(5)可简化为

式中,Is在阈值处很敏感,在阈值以上时,自发辐射基本上可以忽略,Is趋向于0,此时功率与电流的关系式为

当半导体激光器工作在动态调制状态下时,由式(1)和(2)可以推导激光器动态小信号强度调制的频率响应特性,可近似表示为[7,13]

式中,γ是阻尼因子。
经过推导可以得到fr、γ 与电流的关系为

式中,中间值A 的表达式为

对式(12)与(13)进一步推导,可建立γ与f2r之间的关系,即

式中,K为K因子,其表达式为

通常带宽测试中存在RC 等寄生参数,考虑寄生参数的激光器幅频响应特性表达式为[14]

由于寄生参数与偏置电流无关,而探测器的响应在测试中也认为是不变的,同样与偏置电流无关,因此可以利用不同偏置电流下的S21参数提取本征激光器fr与γ。利用小信号测试系统测得不同偏置电流下小信号幅度频率响应求差值可得H21(f),用对数坐标可表示为

利用式(18),结合测试得到的半导体激光器在不同电流下的S21曲线,可提取激光器的fr与γ,具体实例在结果与分析中。通过此种方式拟合的参数值,忽略了半导体激光器在高电流下较为明显的增益压缩效应,通过对参数提取的公式进行推导和查证,可得到其成立的条件为[5-6]

式中,Z=4π2f2r+1/2γ2,为中间变量。
在低电流下,2Z/γ2的比值较大,式(19)的条件基本成立,但是随着激光器工作电流的增大,γ值增大,2Z/γ2的比值减小,式(19)条件成立的可信度降低,利用式(18)提取fr与γ得到的结果是不准确的。而当激光器工作在微波通讯系统时,需要分析器件工作在大电流状态下的性能,此时激光器增益压缩效应明显。因此,在分析激光器工作在大电流状态时,需要考虑激光器在大电流下的增益压缩效应,更为精确完整的激光器小信号频率响应表达式为[5,15]

利用式(20)可得到提取激光器fr与γ更为准确的表达式
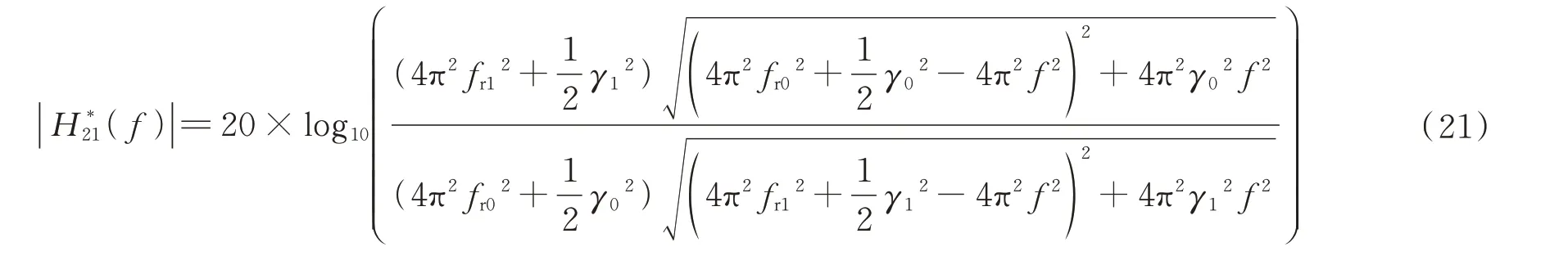
通过一系列公式的推导,得到f2r以及γ与I更为准确的关系式如下

根据上述关系式可建立γ与f2r之间的关系

根据设计的激光器结构可计算得到Γ、V,结合以上数值分析,通过一系列的运算,即可求得速率速率方程式(1)和(2)中的所有参数值,其详细的提取方法和计算结果记录在第2 节的结果与分析中。
2 结果与分析
所分析的半导体激光器是本课题组自行设计和流片的分布反馈激光器(Distributed Feedback Laser Diodes,DFB LD),将流片得到的激光器芯片贴装在高速接地共面波导(Grounded Coplanar Waveguide,GCPW)上,裸芯片通过锥形光纤耦合进系统。通过光矢量分析系统测得激光器在不同偏置电流下的小信号频率响应曲线(S21),如图1(a),工作电流设置范围为20~90 mA,可以看出,随着偏置电流的增大,激光器小信号调制响应带宽增大,响应曲线愈趋于平坦。通过直流测试系统可测得激光器的P-I曲线,如图1(b),可以看出,激光器在偏置电流为0~100 mA 内保持着良好的直流线性度。

图1 不同偏置电流测试下的半导体激光器响应曲线Fig.1 The response curve of a semiconductor laser on different bias currents
采用传统的参数提取方法,根据式(18)对不同电流下的S21曲线进行拟合,得到激光器的fr与γ,如表1中所示,标注为传统方法提取结果。根据式(21)拟合的结果同样标注在表格中,并标示为本文方法。利用表1 中的fr与γ值,绘制出f2r与偏置电流I的关系曲线并利用式(12)进行线性拟合,得到的拟合结果如图2(a)。激光器的偏置电流I取值范围为20~90 mA 时,线性拟合的曲线与提取的参数值并不完全重合,由式(12)可知,理论上f2r与I应该为完美的线性关系。同时从图中可以看出,当I的值在20~40 mA 时,f2r与I基本呈线性关系,符合式(12)。文献[4,16]中提取fr与γ值时基本上都是采用此种方式,同时针对激光器的工作电流也比较低。绘制出f2r与γ的关系曲线并利用式(15)进行线性拟合,如图2(b)所示,发现在低电流下重合性好,在高电流下的重合性还是欠佳。因此,认为用以往传统提取方法得到的参数值在低电流下是准确的,但是在高驱动电流下,其结果准确性存疑,而且用此种提取方法无法直接得到速率方程式(1)和(2)中的所有参数,存在明显的不足。
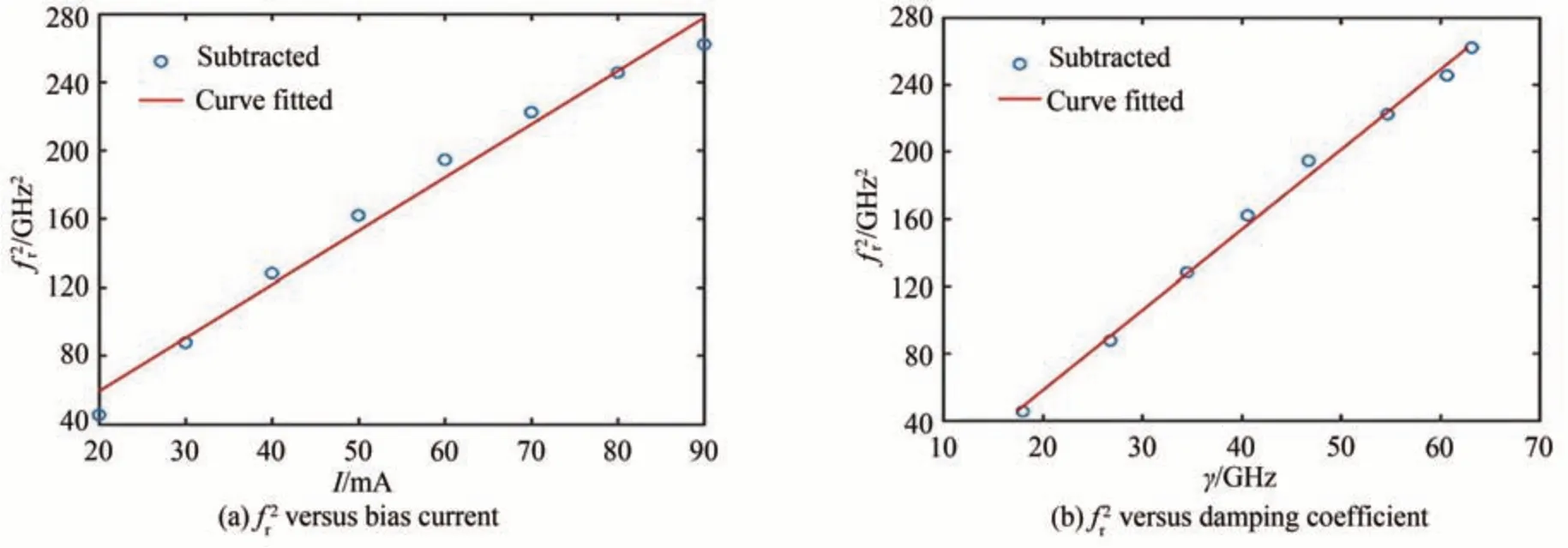
图2 不同偏置电流和阻尼因子对应谐振频率f2r 拟合值与参数提取值对比Fig.2 The value comparison between curve fitting and parameter subtracted data in terms of different bias currents and damping factors

表1 利用式(18)(传统方法)和式(21)(本文方法)分别拟合得到的fr 与γTable 1 The fitting results of fr and γ obtained by traditional subtraction method according to Eq.(14)and improved parameter extraction formula according to Eq.(21)respective
根据表1 的计算结果,可进一步计算得到2Z/γ2的比值,如表2。

表2 表达式2Z/γ2 的计算值Table 2 The calculated value of2Z/γ2
从表2 中可以看出,随着激光器驱动电流的增大,2Z/γ2减小,高电流下计算得到的值约为低电流下的1/2,因此在高工作电流下,式(19)的条件并不成立。利用表2 的数据对条件式(19)进行过详细的分析和计算,此计算结果同时也验证了对图2 的分析。因此,当激光器工作在高偏置电流下,需要用完整的参数提取式(21)进行拟合计算。利用图1(a)中的S21曲线对流片制作的DFB 激光器进行参数提取,工作电流范围为20~90 mA,得到的fr与γ如表3。其拟合曲线如图3,其中图3(a)为利用20 mA 与40 mA 进行拟合时的图像,图3(b)为利用20 mA 与60 mA 曲线进行拟合时的结果,其他电流下的拟合曲线基本相似,可以看出拟合曲线重合性的很好。

图3 利用不同电流下的S21曲线拟合出fr 与γFig.3 The fitting results fr and γ according to S21 curve on different bias currents
对比表1 中传统方法和本文方法提取结果,可以看出在宽电流范围内,阻尼因子γ的值都很接近。低电流下fr的值相差不大,而随着DFB 激光器偏置电流的增大,前后两种方法提取的fr差值逐渐增大。利用表3中的数据,可计算得到Z的值,将其与电流I作图,并利用式(22)进行拟合,如图4(a)。同理可以画出f2r与γ的关系曲线,并分别利用式(24)进行拟合,可以得到K与τn的值。
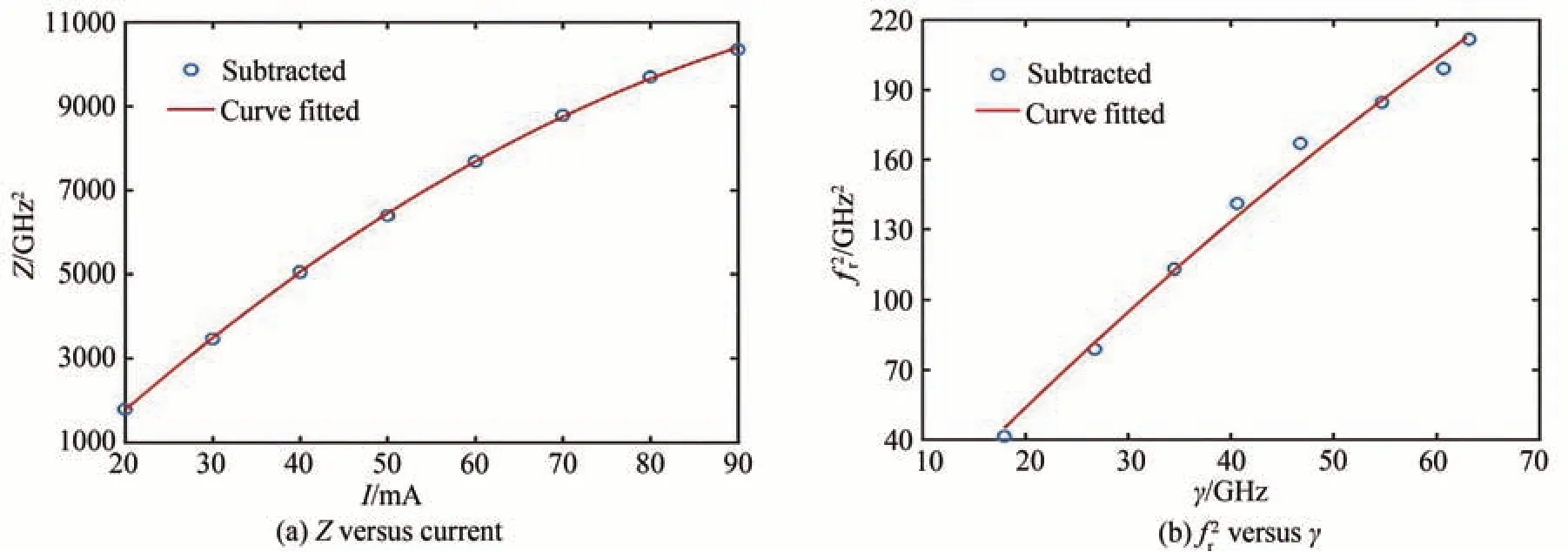
图4 不同偏置电流和阻尼因子对应谐振频率f2r 和中间变量Z 的拟合值与参数提取值对比Fig.4 The value comparison of f2r and Z between curve fitting and parameter subtracted data in terms of different bias currents and damping factors
从Z与I的关系图4(a)可以看出,在20~90 mA 宽电流范围内,激光器提取的结果与式(20)完美拟合,呈二次关系,与图2(a)对比拟合效果明显更好。从图4(b)可以看出,fr与γ的关系与式(22)也基本上重合,与图2(b)对比,同样拟合效果更优。因此,可以认为通过这种方式提取的fr与γ是更加准确的,更加接近真实的值。
根据激光器的结构进行计算,取V=18 um3、Γ=10%,结合数值分析与图1(a)中测试得到的P-I曲线,可以得到速率方程式(1)和(2)中的所有参数值,如表3。

表3 利用改进过的方法提取得到的激光器参数值Table 3 The subtracted laser parameter values by a new improved method
到此,提取了半导体激光器宽电流下的fr与γ,同时得到了速率速率方程式(1)和(2)中的所有参数值,之后便可利用得到参数值来分析激光器性能。此种方法要求的测试项目少,提取简单方便,成本低,在科研和工程中都极具意义。
3 结论
本文改进传统的参数提取公式,利用S21曲线即可提取得到fr与γ,在此基础上,结合常规的P-I曲线,即可得到速率方程中的参数。该提取方法可以在较宽工作电流下得出准确的fr与γ值,在此基础上得到了相对准确的半导体激光器速率方程的各种参数值,有助于快速地计算和评估激光器的各项性能指标,快速地找出优化激光器性能的方向。

