考虑驾驶行为的电动汽车电池电压预测方法*

朱 曼 谢宗锐 张 晖▲ 陈 枫 马 枫 李少鹏

（1. 武汉理工大学智能交通系统研究中心 武汉 430063；（2. 武汉理工大学国家水运安全工程技术研究中心 武汉 430063）

0 引 言

在环境污染和能源危机的压力下，以电动汽车为代表的新能源汽车已成为未来的发展趋势和全球竞争与发展的焦点[1-2]。根据公安部发布的统计数据：截至2022年6月底，国内新能源汽车保有量已经达到1 001万辆，占汽车总量的3.23%，其中，纯电动汽车保有量810.4 万辆，占新能源汽车总量的80.93%[3]。2022年1—8月，我国新能源汽车销量386万辆，其中纯电动汽车销量304万辆，电动汽车占新能源汽车比例达78.76%，可以看出电动汽车是新能源汽车主要的组成部分[4]。

纯电动汽车的电池系统是其核心竞争力，动力电池的性能对电动汽车的整体性能和发展前景起直接决定作用[5]。锂离子电池以其能量密度高、无记忆效应、寿命长等优点，逐渐成为了动力电池的首选[6-7]。电池系统中单个电芯的电路故障，会导致整个电池组出现故障，直接影响电池系统的正常运行，严重时电池内部会出现热失控，甚至导致着火、爆炸等事故，严重危及乘员的财产和人身安全[8]。因此，需要高效的电池管理系统(battery management system,BMS)来确保电动汽车的安全运行，实现电池系统的健康状态估计[9-10]。电压作为电池系统的核心参数，对电池电压进行准确的预测是保证电池系统健康的关键，精准的电池电压预测可以对实现车辆实时监测电池系统健康状态提供理论支撑。但现有的文献在电动汽车运行研究方面，鲜有将动力电池系统与驾驶行为结合考虑的情况。Neubauer等[11]测试了不同驾驶行为和气候对电动汽车能耗变化和行驶里程的影响，发现极端环境和激进驾驶员的驾驶行为会使动力电池的峰值温度过高和电池的过度退化。梁海强等[12]发现激进的驾驶模式会加剧电池老化，老化速率整体比温和型的驾驶模式快1.73%～10.37%。可见，驾驶行为的变化极大影响着电动汽车动力电池的状态，因此，要提升电动汽车运行安全性，实现对电动汽车动力电池电压更精准的预测，结合驾驶行为参数尤为重要。

Feng 等[13]利用最小二乘法搭建了三维电化学-热-内部短路(internal short circuit,ISC)耦合模型，探索了测量的电压、电流和温度与ISC 状态之间的相关性。Zhao等[14]研究了1种将锂离子电池动态精确建模与递归神经网络(recurrent neural network,RNN)在不同工况下的故障诊断方法，该模型能够准确预测电池电压，误差小于5%。Yao 等[15]提出了1 种基于电网搜索SVM的电池系统智能故障诊断方法，可以识别潜在的故障状态并对故障的严重程度进行分类。在车辆运行过程中，驾驶人不同的驾驶行为特征使车辆处于不同的驾驶工况下，而不同的驾驶工况会使得动力电池的相关参数如电压、电流等出现不同的波动变化，在2019 年Hong 等[16]发表的文章中，首次考虑了驾驶行为对电池电压的影响，通过研究发现制动踏板行程值、速度等驾驶行为与电池电压存在显著的相关性，并利用长短时记忆神经网络(long short term memory，LSTM)提出了1 种新颖的电压故障诊断和预警方法，但该研究的数据颗粒度低，低频率的数据可能难以反映出电池电压的跳动变化。

针对现有的电动汽车电池电压预测研究采用的数据颗粒度较低、少有结合驾驶行为、动力电池电压预测精度低的问题，基于自然驾驶实验采集的精细化纯电动汽车历史运行数据，研究了车速、加速度、加速踏板行程值、制动踏板行程值等驾驶行为参数与动力电池电压的相关性，采集精细化的电动汽车数据，基于LSTM构建了电压预测模型，提前预知电池电压的波动，并且优化了电池电压预测模型，提高了电池电压预测的精度，为保证电动汽车电池的健康运行提供有力的理论支撑，保障电动汽车全生命周期安全运行。

1 实验数据采集与处理

1.1 自然驾驶实验

为了充分考虑驾驶过程中的随机性和驾驶路段多样性，确定使用东风某车型作为实验车型，以此设计了电动汽车自然驾驶实验。实验通过T-BOX、ADAS 和三轴陀螺仪设备采集高精度（所有参数采样频率均≥1 HZ）的电动汽车动力电池参数（电流、电压、SOC、温度等）、驾驶行为参数（速度、加速度、制动踏板行程、加速踏板行程等）。结合本研究的具体要求，最终在20辆电动汽车中加装实验设备来完成本次实验和研究。

自然驾驶是驾驶人驾驶自身车辆在实际道路上行驶，整个实验的周期较长，且实验过程的数据记录是在不干扰驾驶人正常驾驶的前提下进行，其目的是获取最贴近驾驶人自然生活的驾驶数据。本文选择的是东风某镍钴锰酸锂电池的纯电动车（见图1），该车型的车辆信息见表1。

表1 电动车车辆信息Tab.1 Electric taxi vehicle information

图1 实验车辆Fig.1 Experimental vehicle

自然驾驶实验中，先后选择了20名正常驾驶员进行实验，20 名驾驶员身体健康，驾龄均为5 年以上，人口统计学特征见表2。

表2 实验人员统计学特征Tab.2 Statistical characteristics of the experimenter

此外，该实验在GB/T 32960.3—2016《电动汽车远程服务与管理系统技术规范第3 部分：通信协议及数据格式》[17]规定的新能源汽车实时信息上报数据种类的基础上，还另外采集驾驶人驾驶行为数据和汽车运动状态数据。采集的部分字段信息见表3。

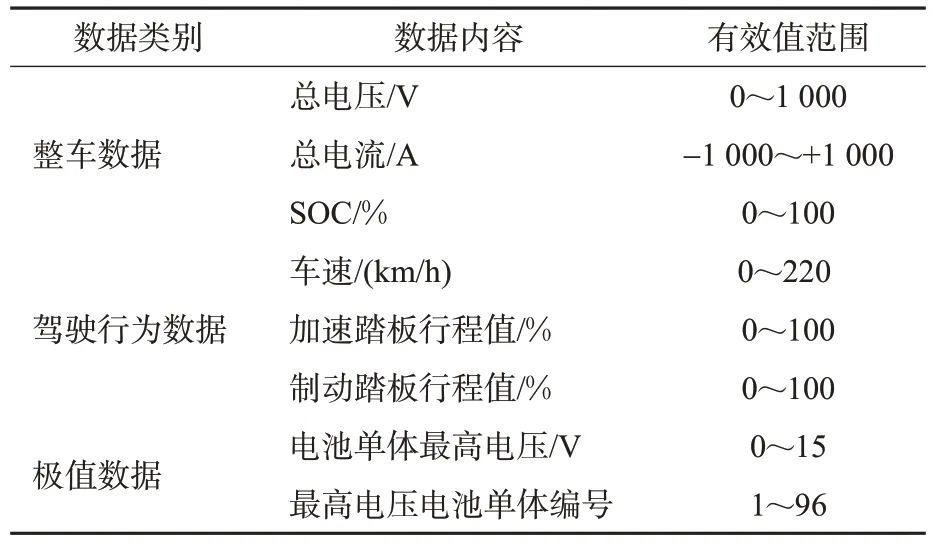
表3 实验采集部分字段信息Tab.3 Experimental collection of partial field information

确定了实验车辆、实验人员、实验数据采集/存储设备以及后续研究所需要的数据字段，在武汉市开展了本次自然驾驶实验，采集了2022 年2 月—11月共10个月的电动汽车自然驾驶实验数据。

1.2 数据预处理

由于传输丢包和获取错误，车辆全生命周期数据中存在大量无效项和错误帧。为了准确高效地分析数据，需要根据合理的数据处理规则对数据进行清洗，这样可以在不排除干扰项的情况下，最大限度地保留数据特征，提高分析效率。采用的数据处理规则见表4。

表4 车辆数据处理规则Tab.4 Rules for vehicle data processing

完成数据清洗后，为了更好的分析不同的驾驶工况与动力电池参数间的关联影响，需要对主要分析的参数实现数据时间对齐，驾驶行为中，加速踏板行程值、制动踏板行程值和加速度的采样频率为10 Hz，按照该采样频率对高采样频率数据进行数据整合。

为了尽可能保留高频数据所保留的信息，本文使用滑动平均方法对高频数据实现数据合并。计算见式（1）。

式中：yn为第n个参数的滑动平均计算结果；M为计算窗口的长度，即采样频率；xi为i秒内的所有数据。最终经过数据预处理得到的数据样例见表5。

表5 数据整合表Tab.5 Data integration table

2 驾驶行为参数与电池相关分析

2.1 驾驶工况与电池参数变化规律分析

电动汽车在运行的过程中，随着驾驶行为的变化会出现多种驾驶工况，不同的驾驶工况对应着电动汽车不同的输出，即对应着不同的电池电压、电流等多维特征值的变化[18]。

由上述可知，驾驶工况决定着放电过程特性，也影响着动力电池的状态。为了准确地分析驾驶工况对动力电池参数变化的影响，首先需要确定驾驶行为的表征参数，保证后续研究不同驾驶工况下动力电池参数变化规律的可靠性[19]。基于以往的文献，本文选取研究分析的驾驶行为参数包括加速踏板行程值、制动踏板行程值、车速、加速度。

根据获取的电动汽车实时运行数据进行电池组电压、电流、SOC等动力电池参数随驾驶过程中工况变动的动态变化规律分析。选取车辆1某天运行时长为60 min的片段进行分析，时间跨度为17：10—18：10。由于数据采样的频率较高，采集的数据量足够精细，并且数据量较大，选取的片段能够较好反映驾驶工况与电池参数变化规律。根据得到的加速踏板行程值、制动踏板行程值、车速、电池组电压、电池单体电压、电池电流、SOC数据，绘制的变化曲线见图2。

由图2 可见：加速踏板行程值变化决定着电池组电压与电流的起伏变化：电流与加速踏板行程值的变化轨迹一致的，呈正相关，加速踏板行程值增大时，电流增大，反之亦然；而电压与电流是呈对称反向变化的，即电流增大时，电压下降，电流下降时，电压上升，所以电压与加速踏板行程值的变化轨迹相反，呈负相关。这是由于当驾驶人踩下加速踏板，使行程值增大时，车速增大，意味着此时动力电池组需要增大功率输出以驱动车辆加速行驶，所以电池组的输出电流会随之增大，而电压会随之减小。

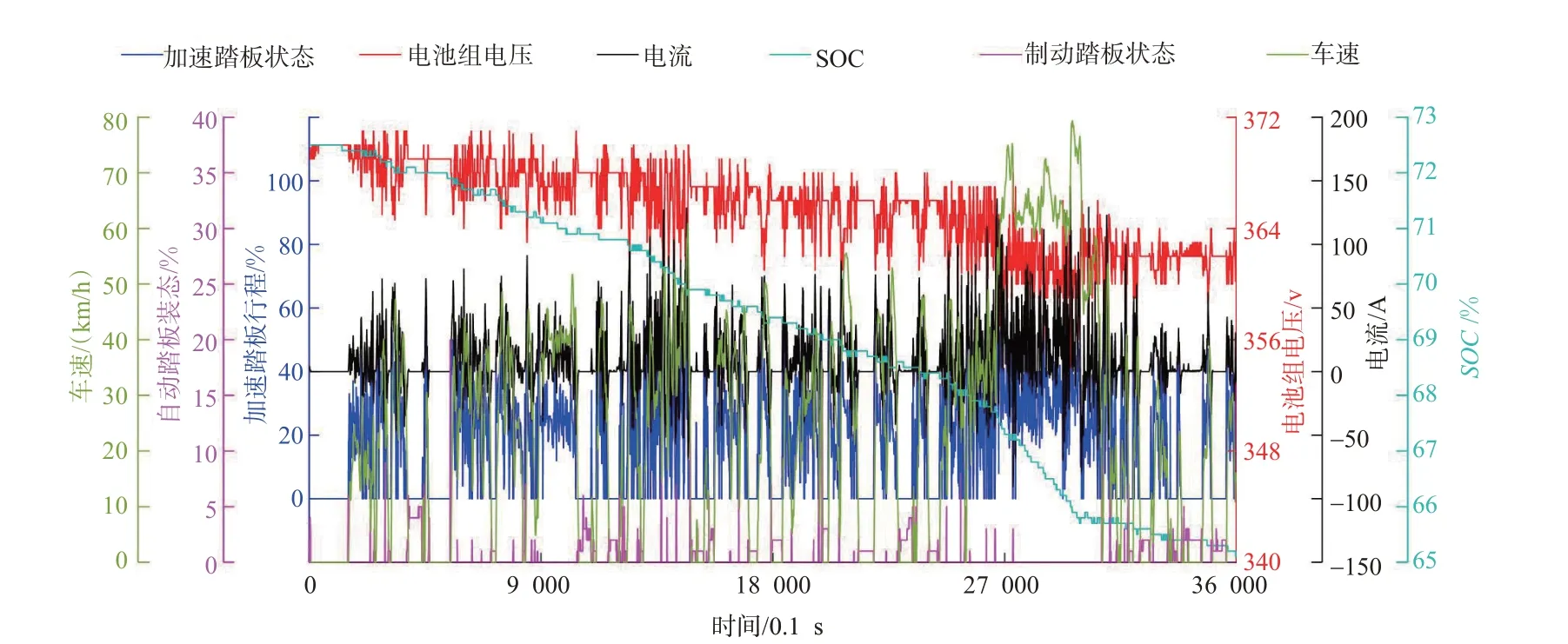
图2 车辆1运行时长为60 min的片段Fig.2 Asegment of vehicle 1 running for 60 minutes

加速踏板开始处于完全松开状态的时刻起，电压会从当前值逐渐上升，直至达到最大电压值，此过程与电流减小至0 然后继续减小至负向最大电流保持一致。之后，电压值随着车辆减速而逐渐减小。若在电压减小的过程中，驾驶人踩下制动踏板，此时电压再次开始增大直至最大值，而后逐渐减小至稳定值，此时表明能量回馈结束。此阶段下，加速踏板完全松开时的车速越大，则可达到的最大电压越大。

2.2 驾驶行为参数与电池参数相关系数计算

确定与电池组电压相关的特征参数，利用皮尔逊相关系数进行相关性分析，本次分析提取的动力电池参数包括：电池组电压、电池单体电压、总电流、电池SOC、探针温度；驾驶行为表征参数包括：加速度、加速踏板行程、制动踏板行程、车速；此外，本次分析还提取了环境温度数据进行计算。

皮尔逊相关系数，又称皮尔逊积矩相关系数，是用于度量2组数据X，Y之间的线性相关性，其值介于-1～1 之间[20]。皮尔逊相关系数的值越接近1，表示2 组数据的相关性越强。2 个参数之间的相关性可通过绝对相关系数值进行评估：极强相关（0.8～1.0），强相关（0.6～0.8），中度相关（0.4～0.6），弱相关（0.2～0.4），极弱相关（0～0.2），驾驶行为参数与电池参数相关系数计算结果见图3。

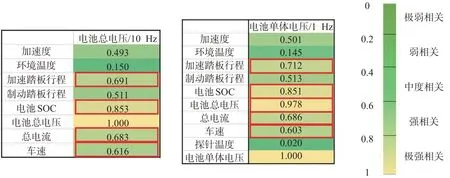
图3 电池组电压与各参数间的相关系数Fig.3 Pearson Correlation Coefficient between battery voltage and parameters

由图3 可见：电池组电压（也称为电池总电压）和各参数之间的相关系数与电池单体电压的计算结果非常接近，并且二者本身就具有极强的相关性；以电池单体电压为例，电池SOC、电池组电压与电池单体电压极强相关，相关系数分别为0.851，0.978，加速踏板行程值、总电流、车速与电池组电压强相关，相关系数分别为0.712，0.686，0.603。制动踏板行程值、加速度、环境温度、探针温度与电池单体电压相关性较弱。

通过相关性分析结果，最终确定了与电池组电压相关的驾驶行为、动力电池特征指标：加速踏板行程值、车速、电池SOC、总电流。

3 预测模型与方法

3.1 LSTM神经网络模型

长短期记忆神经网络（long short term memory，LSTM）是最经典的带有门控结构的递归神经网络（recursive neural network，RNN）。RNN 是1 类面向时间序列结构进行建模的人工神经网络，时间序列往往具有十分显著的前后依赖关系，而RNN引入了时间维度的循环连接，在不同时间点添加新的隐藏层，使整个神经网络具备了对时间序列前后状态的建模能力，这就表示RNN 的输出除了作为运算结果，也可以成为下一时刻的输入信息，影响下一时刻的输出。正因为这一特性，RNN 在文字识别、交通流预测等方面具有良好的应用前景。

然而，标准RNN 的缺点是不能忽视的，它存在长期依赖问题，在较远的时间步长中，其反向传播的过程存在梯度爆炸或消失[21]。LSTM 因其特有的门控结构，在捕获长时时间序列方面取得了更大的成功，因此该模型在时序数据的研究领域中得到了更广泛的应用。在LSTM 中，有2 个重要参数，即门结构和单元状态。LSTM 的关键是单元状态，该模块类似于传送带，实现LSTM 中的数据传输。门结构是1 种按需传输信息的方式，在LSTM 中，包含3 类门结构：遗忘门、输入门和输出门，可以向单元状态添加或删除信息。LSTM 结构见图4。

图4 LSTM网络结构Fig.4 LSTM network structure

LSTM模型中在LSTM 模型的训练过程中需要设置和优化许多参数，主要包括时间步长（time stamp，TS）、学习率（learning rate，LR）、批处理大小（batch size，BS）、LSTM/全连接神经元个数（LSTM units/ dense units）、LSTM/全 连 接 神 经 网络 层 数（LSTM layers/ dense layers）、随机失活因子（dropout factor）、训练次数（epochs），具体含义见表6。

表6 LSTM 超参数Tab.6 LSTMhyperparameters

训练LSTM 模型的这些参数需要很长时间，尤其是当模型具有大型数据集时。但是，不可能在短时间内将参数调整到最优。因此，应根据经验设置1组可操作的超参数，这些参数需要逐步优化以获得优化的模型，实现更精准的预测。

3.2 考虑驾驶行为的电动汽车电池电压预测建模

根据上文的相关性分析结论，利用电池电压与行车工况之间的映射关系，以驾驶行为参数和动力电池相关参数作为特征用于训练。将电池组电压、总电流、电池SOC、加速踏板行程值、车速这5 个参数作为输入，电池组电压作为输出，训练并测试LSTM 模型，实现对电动汽车电池组电压的预测。使用python 编程语言中的keras 高级神经网络应用程序编程接口搭建电池组电压预测模型。

在每次前向传播结束时，LSTM 的预测电压与真实电压之间的差异可以通过损失函数计算。对于电池组电压这类连续数据，采用均方误差（mean square error，MSE）损失函数，计算见式（2）。

式中：N为序列的长度，与输入时间步长单位一致；Volt为预测电压值，V；Volt*为实际电压值，V。

LSTM 电压预测模型结构见图5。

图5 LSTM电压预测模型结构Fig.5 LSTM voltage prediction model structure

根据本文的研究目标，由于车辆4，5 含有故障数据，因此选用其他18 辆车的数据作为研究对象，以车辆1，6～20 的正常运行数据作为模型输入进行预测建模，训练集与测试集的数据比例为8∶2。

由4.1可知：LSTM建模首先需要根据经验设置1组可操作的超参数，此处初始设置的1组超参数见表7。初始设置的TS=10，这是由于电压数据不具有周期性，且电压的变化受驾驶行为的影响，因此输入的时间步长较小，单次只输入1 s的数据用于模型训练。

表7 LSTM 模型初始设置参数Tab.7 LSTM model initial set parameters

驾驶行为参数与电动汽车内部参数的数据维度存在差异，为了降低不同数据间存在的量纲差异，更好地结合驾驶行为数据与电池数据，减少极端数据带来的数值影响，同时提升LSTM模型的计算速度，用式（3）对输入的数据进行0-1归一化处理。

式中：k为数据维度；X为原数据；Xmin为数据的最小值；Xmax为数据的最大值。

对于评价回归预测的结果，通常会使用平均绝对误差（mean absolute error，MAE）、平均相对误差（mean relative error，MRE）、均方误差（mean square error，MSE）、均方根误差（root mean square error，RMSE）等多个指标进行评价。为了评估训练良好的LSTM 电池组电压模型的预测性能，本文使用MSE和MRE这2 个指标来评价模型的预测结果。MRE的计算见式（4）。

式中：n为训练或测试样本的数量；为电池系统的预测电压0值,V；Ui为真实电压值，V。

基于预先设定的超参数，电池组电压的预测结果见图6。此时预测电压和实际电压间的MRE≈0.17%，MSE≈0.70，2个数值结果表明LSTM模型已经取得了较好的预测结果，预测的电压值较接近真实的电压值。由图6 可见：在实际电压出现极小值的时间点，尤其是在750～2 000 s时间段的极小值电压，预测电压值不能准确地反映当前的极小值电压；并且在1 250～1 750 s时间段里，预测值在极大值点接近真实值，但在380～381 V的电压区间里，预测值与真实值存在着一定的偏差，拟合的效果没有很好地反映出真实电压的走势。

图6 初始超参数下的电压预测结果Fig.6 Voltage prediction results under initial super parameters

为了达到更好的预测效果，需要对模型的超参数进行优化。超参数优化的方法主要有3 种：网格搜索法、随机网络和贝叶斯优化[22]。随机网络和贝叶斯优化方法一般适用于千万级别以上的数据量，这样可以降低模型训练的复杂度，但使用这2 种方法时，如果一旦找到了1个局部最大值或最小值，它会在该区域不断采样，所以它很容易陷入局部最值。而对于本文所训练的车辆数据，样本数量约为7 000 000，样本数据量不算庞大，可以使用网格搜索方法（grid search,GS）寻找最优参数。GS 算法利用穷举法优化模型参数，设置参数及取值范围，将范围内所有网格节点取值代入模型计算，本文利用MSE作为评价指标，以每2个超参数为1组，使用GS算法进行迭代优化。

GS算法通过试错法确定1组超参数作为原始样本网格，训练LSTM 模型并计算原始样本网格的MSE，计算样本网格附近所有网格对应超参数下的MSE，选择MSE局部最小的网格作为新的样本网格，直到所有相邻网格对应的MSE都大于中心样本网格的MSE。最终，选择最近的样本网格的超参数作为最终的超参数。优化流程见图7。

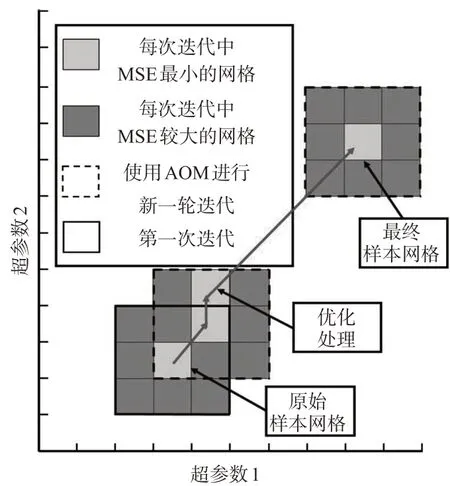
图7 超参数优化流程图Fig.7 Hyper parameter optimization flow chart

利用所述的超参数优化步骤，最终确定了预测模型最优的超参数，见表8，对应的最优超参数预测结果见图8，预测结果的最小MSE=0.46。

图8 参数优化后电压预测结果Fig.8 Voltage prediction results after parameter optimization

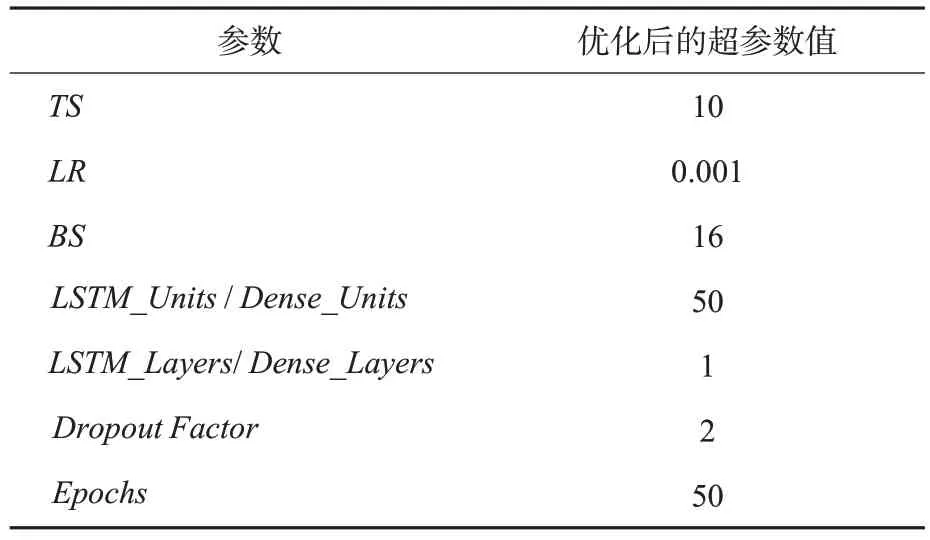
表8 LSTM 模型优化后的参数Tab.8 Parameters after optimization of LSTM model

此时在测试集中，真实值与预测值间的MRE=0.13%，MSE=0.46，优于初始超参数设置的结果；并且在380～381 V 的电压区间里，相较于初始超参数的预测结果，预测值与真实值实现了较好的匹配，电压的走势也更加贴合实际的电压值，体现了优化参数后模型良好的预测效果。

4 预测模型验证

4.1 模型优越性验证

一般的前向传播神经网络只能建立输入输出一对一的映射，而LSTM 得益于其内部的时间步长概念，可以拓展为序列间的映射，因此构建LSTM神经网络时，可以形成一对一、一对多、多对一或者多对多的映射关系。本文所采用的是五对一的模型结构来实现电池组电压的多步前向预测。为了验证所使用模型结构的优越性，比较了一对一（电池组电压单变量预测）和只考虑动力电池参数影响的三对一（电池组电压、电池SOC、总电流）映射关系下各预测模型的MRE和MSE值。在相同超参数的前提下，三对一LSTM模型的MRE和MSE值分别为0.20%和0.986，一对一LSTM模型的MRE和MSE值分别为0.22%和1.02，均高于本文所提出的五对一模型，见图9。由图9可见：只考虑单一特征输入的电压预测模型比多特征输入的电压预测模型预测准确率低，因此表明驾驶行为特征参数也应是电池组电压预测所需考虑的重要因素。

图9 不同电压预测模型结构预测精度分析Fig.9 Analysis of structure prediction accuracy of different voltage prediction models

此外，为了体现模型较好的预测精度，本文将该模型与其他文献中常用的方法进行横向的对比分析。正如引言中提到，相关的学者在他们的研究中同样也实现了精确的电压预测[14,16]，他们分别使用RNN模型、LSTM模型进行研究，数据的采样频率为0.1 Hz，预测精度分别为文献[14]的预测MRE＜5%，文献[16]的预测MRE=0.56%，MSE=0.61，见表9。

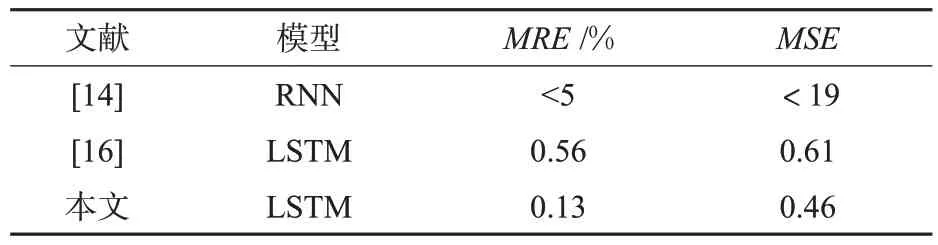
表9 电压预测精度对比Tab.9 Voltage prediction accuracy comparison

本文对电池组电压的预测的MRE和MSE分别为0.13%和0.46，均显著低于上述2 种方法，在横向对比2 篇电池电压预测文献时，本文的模型在预测的精度上显著优于上述文献的方法。结果表明：考虑驾驶行为参数能更好地预测电池的电池电压参数，并且反向验证了驾驶行为参数对电池的影响。

本文使用了武汉自然驾驶实验的高精度数据，使用高精度的数据（10 Hz）能更精确的反映驾驶行为对电压的影响，更细致地挖掘电压的变化状态。因此，本文提出的方法比其他方法具有更优越的预测性能。

4.2 模型鲁棒性验证

为了验证LSTM 模型对电池组电压预测的鲁棒性，选取另外2辆未发生故障的车辆（车辆2、车辆3）数据输入至模型中用于模型的测试验证，2辆车均选取了2022年3月6日的数据作为模型输入数据，车辆2数据的起始时间为14：40—15：00，车辆3数据的起始时间为16：47—17：07，利用MSE和MRE这2个指标评估LSTM模型的预测的准确程度。2辆车的预测结果见图10，车辆2、车辆3 预测电压和实际电压间的MRE分别为0.15%，0.17%，MSE分别为0.50，0.55，2 辆车的预测精度均优于文献[14]和文献[16]的预测结果，模型预测的准确性、有效性得到进一步验证。

由图10 可见：2 辆车预测的结果曲线在电池电压运行走势上能保持较好的一致性。车辆2的预测结果见图10(a)，预测曲线虽然未能达到部分极端的电压极小值点，但在总体的电压走势与实际电压基本保持一致，并且在极大值电压点基本与实际电压保持一致；车辆3 的预测结果见图10(b)，总体的电压走势与实际电压也基本保持一致，并且预测电压的极值点接近实际电压的极值点，因此认为该模型可以较好地反应电压未来的走势，可以为电动汽车电池健康预警提供理论的支撑。

综上所述，本文搭建的LSTM 模型表现出了良好的预测性能，预测电压与真实电压比较接近，并且该模型能够准确预测出电压的未来走势，模型的鲁棒性和准确性得到了保证。

5 结束语

通过开展电动汽车自然驾驶实验，探索驾驶行为对电动汽车动力电池参数变化的影响，构建了基于LSTM 神经网络的电池组电压预测模型，采用网格搜索法对预测模型中的超参数进行优化，并采用均方误差和相对平均误差指标计算模型预测的准确率，结果表明优化超参数后的模型表现更佳。同时，将结合了驾驶行为参数的预测模型与一对一架构和只考虑动力电池参数的多对一架构进行比较，考虑驾驶行为参数的五对一模型有效提高了电动汽车电池电压预测的精度，验证了预测模型的优越性；选取其他2 辆正常运行的车辆，将2 辆车的数据输入至该模型中进行电压预测，预测的结果能够较好地拟合车辆运行过程中的正常电压，并且预测的精度均得到提高，优于横向对比的文献[14]和文献[16]，进一步验证了模型的鲁棒性，为实现电动汽车动力电池电压异常风险预警提供了模型支撑，对电动汽车的运行安全研究具有一定指导意义。本文虽然通过研究取得了一定的成果，但由于数据样本的限制，且对故障本身缺少一定的机理研究，在动力电池内部机理深入分析等方面存在一定的不足。针对本文的不足，需要在未来的研究中逐步完善和补充。

1）增大预测模型输入样本量，并对超参数进行进一步优化，实现更精准的电压预测。对于LSTM 神经网络而言，输入样本的大小和多样性可以决定训练模型的学习能力。本文输入的正常车辆样本数据无法覆盖车辆运行的全生命周期[23]，因此需要定期更新输入数据集，进一步提升模型的预测效果。

2）对电动汽车故障进行更深入的机理分析，周围环境的温度和湿度对动力电池的内部运行也具有潜在影响[24-25]，可能会导致车辆在运行过程中出现故障，因此，车辆运行的周边环境在实时的车辆故障诊断中能够提供一定的参考价值。