高速公路限速策略优化方法与评价模型*

杨雅钧 张 驰▲ 唐 翔 亓 鑫 赵一静

（1. 长安大学公路学院 西安 710064；2. 长安大学运输工程学院 西安 710064；3. 广西交通设计集团有限公司 南宁 530029）

0 引 言

随着我国经济的发展，公路里程迅速增长，高速公路路网的建设与完善也在快速发展，但与此同时也带来了各种安全问题。交通事故受人、车、路、环境等多方面影响，其中车速过高或失控是最主要的因素之一，超速行驶容易造成各种事故，对安全行车影响极大。因此采用限速手段对公路进行安全管理，可以达到“对症下药、精准治理”的效果。由于限速所考虑的因素复杂多样，行业内并未形成共识，缺乏相关规范的专业支撑，如何让限速更加安全、高效、合理，是需要思考的问题。

对于限速区间的优化方法研究，目前主要为限速区间长度值以及限制速度值确定2个方面。在限速区间长度值的研究中，结合道路行驶状况及线形设计参数，2011 年，徐婷[1]通过VISSIM 仿真软件结合交通量、道路线形以及车辆行驶速度等数据给出了限速区间的设置长度以及过渡段长度的建议阈值；2017年，李瑞等[2]通过构建公路安全与效率指数的评价指标模型，结合理论计算和问卷调查对限速区间长度进行了最小值的标定；2020年，季托等[3]根据高速公路不同断面形式提出分流交织区的限速方案；在设计参数方面，美国、南非等国家通过制定规范的方式对公路中的限速区间最小长度值进行了规定[4-5]。在限制速度确定值研究中，部分学者针对可变限速对交通运行的影响开展研究，2017 年，Zhang等[6]通过对传统可变限速策略进行改进，提出了入口匝道与上游公路延误间的平衡点；2018 年，Papamichail等[7]提出采用比例积分的可变限速控制算法，同时评估了道路通行能力的有效性；2018 年，于德新等[8]在可变限速控制算法中引入速度限制条件，并采用遗传算法求解出了优化模型；2018年，林莉[9]为实现分车道控速的决策参考，提出了不同车型的换道限速模型；2019年，Qian等[10]通过对道路实测限速效果回归，得到双间隔一致性检查可保证变限速控制最稳定，但限速区间行驶时间最长的结论；2020 年，柳本民等[11]以追尾事故数据为样本，对比不同限速条件下的事故百分比，发现道路限速对事故产生的影响较大。在限速方案可信度研究方面，2017 年，Lee等[12]研究发现大多数驾驶人认为限速信息不同于预期速度，提出限速值的确定需考虑限速可信度这一因素；部分研究考虑不同环境条件下的限速策略，如2018年，张驰等[13]首次将雾天不同能见度下车辆横向偏移系数作为评价指标，建立雾天的动态限速模型。

综上，目前国内外关于限速区间长度值的研究大多基于驾驶人角度，主要考虑驾驶人满足视认距离的基本条件，仅能保证驾驶人的行驶安全，忽略了通行效率的降低。关于高速公路限速值的研究，大多只针对某一路段或者全线，缺乏对路段间差异性的考虑，结合路段划分提出限速标准。由于我国地形复杂，很多高速公路地处山区，存在较多大型构造物路段和不良线形路段，路段间差异大。例如山区高速公路中的隧道路段，因其行驶环境封闭，驾驶人行驶过程中难以准确估计车速，需采取交通控制措施以增加行驶安全性，但目前研究较多针对每条隧道的单独限速措施，忽略了山区高速公路中隧道占比较高路段间的行车安全性。为了完善目前我国高速公路中限速相关的理论研究及应用方法，笔者从限速区间长度、划分和优化组合这3 个方面进行分析，提出1 种基于聚类分析的高速公路限速区间确定方法。首先，以满足驾驶人视认标志以及平稳操作为目的，对限速区间最小长度进行了计算分析；其次，以速度突变作为控制因素对高速公路进行了路段分类，并且给出了各个路段限制速度的建议值；然后，基于有序聚类法对限速路段进行优化组合，保证了限速区间的规范性及合理性；最后，通过对我国某山区高速公路进行实例分析，以现有的限速方案与本文提出的限速方案进行对比分析，论证说明本文提出的确定方法的有效性。

1 限速区间长度研究

JTG/T 3381—02—2020《公路限速标志设计规范》[29]中对于限速区间的划分仅给出了推荐划分方式，将限速路段划分为一般限速路段以及特殊限速路段，而没有给出不同类型区间限制速度的具体措施；对于区间长度的规定，仅考虑2种类型路段分类提出统一的参考值，仅规定限速路段的长度不宜小于规范值。难以适应我国线形指标复杂多变的山区高速公路。

限速区间长度的研究理论较为成熟，主要研究限速标志设置条件及驾驶人对限速标志的视认等方面，同时驾驶人对限速信息的接收和处理也十分重要，需要充足的时间保障驾驶人对信息进行反应和操作[14]。

高速公路限速区间长度包括驾驶人对限速标志的视认距离、限速标志设置的前置距离，以及驾驶人的心理稳定距离，见图1。

图1 限速区间组成示意图Fig.1 Schematic diagram of the composition of the speed limit section

1.1 标志视认距离

视认距离为在特定速度下驾驶人能够认清标志内容的最短距离，该距离计算见式（1）[15]。

式中：S为标志视认距离，m；h为汉字高度，m；a为驾驶人视角，°。

相关分析表明：路侧标志最理想的视线偏角为10°～15°[16]，见图2。考虑满足最短视认距离，选取偏移视角最大值20°来进行视认距离的计算。

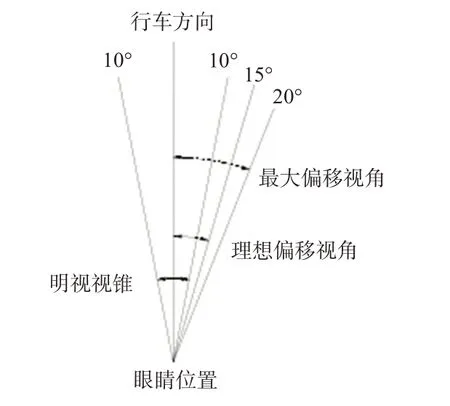
图2 驾驶人视角偏移图Fig.2 Driver's angle deviation figure

运行速度与汉字高度的关系相关规定[17]见表1。

根据驾驶人偏移视角、运行速度与汉字高度的关系相关规定[17]，采用式（1）计算不同速度限制值情况下限速标志视认距离，其取值见表1。

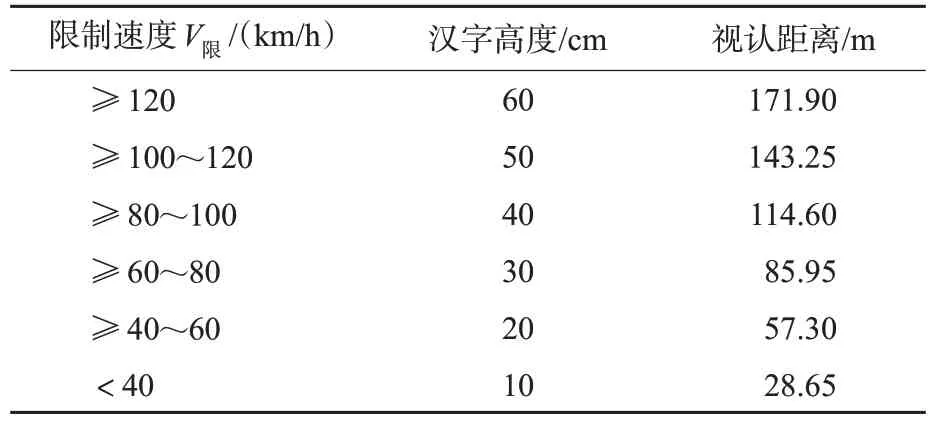
表1 不同限制速度下标志视认距离Tab.1 Sign recognition distance at different speed limits

1.2 标志设置前置距离

前置距离表征限速标志应在距离限速区间起点前的一定距离处设置，从而保障驾驶人从前一路段进入限速区间路段之前有充足的时间按照限速标志内容进行减速、变换车道或采取其它必要措施。本研究前置距离参考GB 5768.5—2009《道路交通标志和标线 第2 部分：道路交通标志》[18]中警告标志的前置距离一般值来选取，其取值见表2。

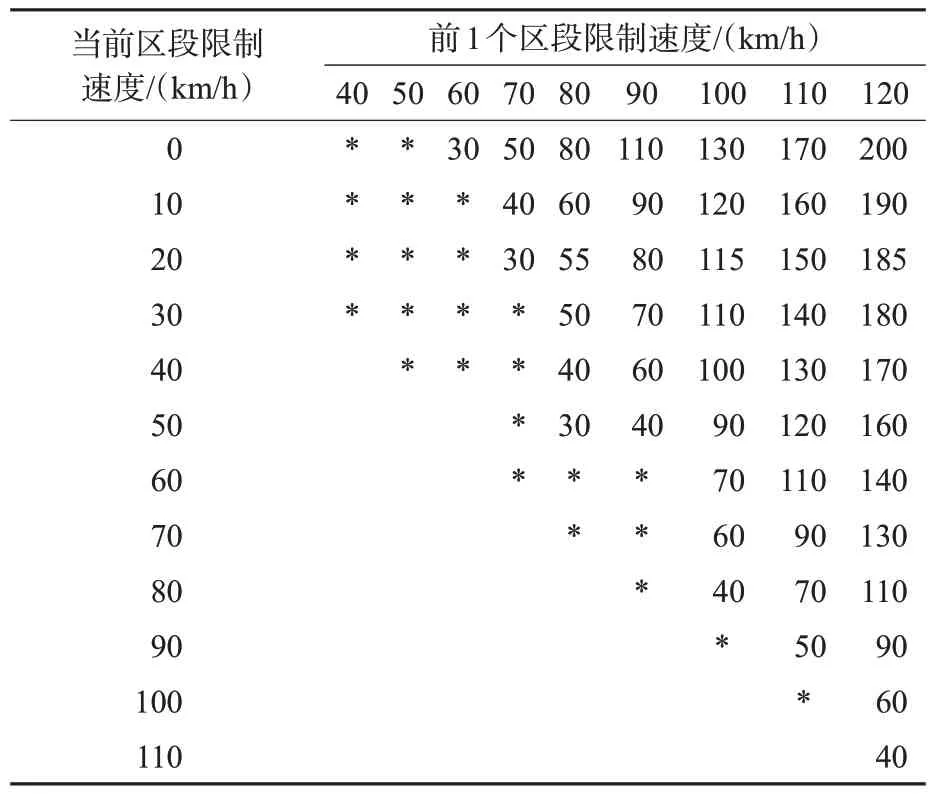
表2 警告标志前置距离一般值Tab.2 The general value of the front distance of the warning sign单位：m

1.3 驾驶人心理稳定距离

当驾驶人驶入限速区间后的一段时间内，驾驶人期望能以平稳的速度（限制速度）行驶，缓解之前一系列行为而带来的紧张疲劳感，另外也为驾驶人适应限速区间的交通环境预留较为充足的时间。

根据交通部公路安全保障工程技术组[19]在不同行驶速度下，当V限≤80 km/h、80 km/h＜V限≤100 km/h、100 km/h ＜V限≤120 km/h时，满足驾驶人心理稳定行驶的最短时间分别为40，72，144 s，计算后其取值见表3。

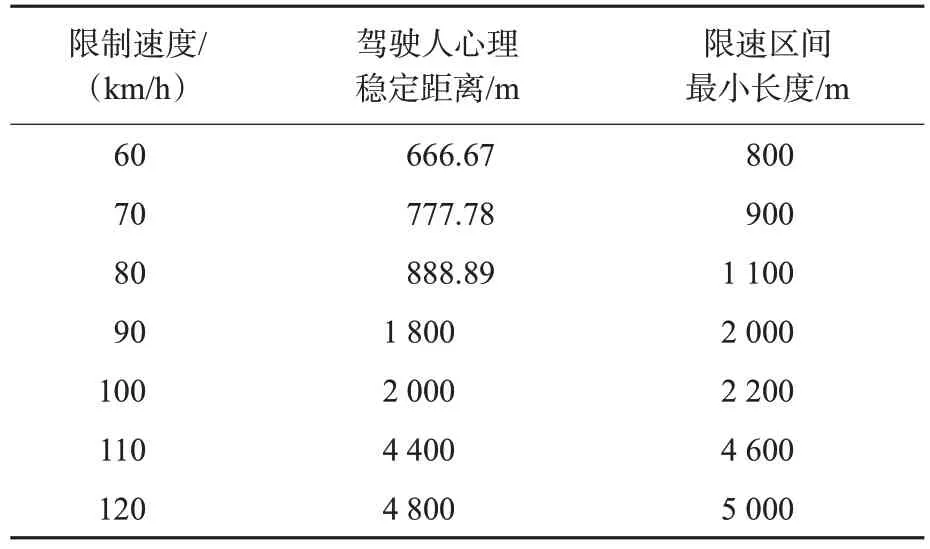
表3 限速区间最小长度Tab.3 Speed limit section minimum length

1.4 限速区间最小长度确定

限速区间的最小长度为标志的视认距离、限速标志设置的前置距离以及驾驶人心理稳定行驶距离最小值的代数和，见表3。为了方便驾驶人遵从限速标志上的信息，按照100 m 为最小单位对计算长度进行取整。

2 限制区间划分

研究表明[20]：发生交通事故时，碰撞车辆瞬时速率变化越大，事故的严重程度也越大，车辆产生的冲击力同样增大，从而发生严重事故的概率也明显上升。因此，为保障行驶车辆的运行安全，需考虑减小车辆的速度差，即降低不同路段间速度的离散性。因此，减少事故发生频率才是高速公路限速管理的根本目的。

根据高速公路事故数据统计以及工程经验分析，高速公路易造成车速突变的路段主要有隧道路段、互通式立体交叉路段、小半径曲线与直线衔接路段、连续下坡路段等，均为高速公路的事故多发点[21]。因此，本文路段划分的依据是是否会产生车速突变。

2.1 划分方法

在研究路段划分时，我国学者通常采用2 种方法来进行，即定长法与非定长法。考虑到在应用到限速区间划分时，定长法最大的缺陷为不能保证限速区间内路段属性保持一致，与实际情况不相符。且当路段存在隧道、立交等构造物时，盲目划分限速区间会降低模型可信度，见图3。

图3 定长法的缺陷Fig.3 Defects of fixed length method

考虑定长法存在上述不足之处，不定长法的“不确定性”更能适应公路中存在多种不同属性路段的特点，并且能够满足多种限速值下的不同限速区间长度的要求，因此本文选择不定长法作为路段划分的方法。

2.2 区间划分

GB 5768.5—2017《道路交通标志和标线 第5部分：限制速度》[23]中规定限制速度应该将道路设计速度作为基准，仅分类对限制速度可提高或减少的值给出了参考值，难以满足随着车辆性能提升，设计速度与实际车速间的差异。

本文采用不定长法将路段分为基本路段、桥梁路段、隧道与隧道群路段、互通式立体交叉路段、长直线接小半径曲线路段、连续下坡路段和复杂组合路段，研究不同路段的限速值确定方式。

2.2.1 隧道与隧道群路段

考虑我国高速公路很多位于山区，山区公路中隧道占比较高，隧道限速成为高速公路限速的难点。目前，我国通常采用设计速度来进行隧道路段的限速管理，因此当隧道洞口前路段线形条件较好时可以结合下述预测模型以及公路设计速度进行限速管理：①平纵线形指标满足3 s 一致性要求；②视距条件良好；③隧道内视线诱导、照明设施设置良好。当隧道洞口前路段线形条件受限时（特别是在山区高速公路中），宜采用设计速度进行限速管理，如：①横断面宽度在洞口衔接处突变；②洞口处设置缓和曲线。

高速公路隧道与隧道群路段的限速取值采用JTG B05—2015《公路项目安全性评价规范》[17]，见表4。

表4 隧道路段运行速度预测模型Tab.4 Prediction model of running speed of tunnel section

2.2.2 其余路段

基本路段及互通式立体交叉路段按照JTG B05—2015《公路项目安全性评价规范》[17]中相关规定进行限速计算。桥梁路段按照GB 5768.5—2017《道路交通标志和标线 第5部分：限制速度》[23]相关规定采取限速措施。

长直线接小半径曲线路段限速值计算采用方超[22]给出的运行速度与半径间的关系式，同时考虑到该模型的适用性后对其进行相关修正，见式（2）。

式中：v曲为限速值，km/h；R为圆曲线半径，m。

连续下坡路段限速值计算采用张驰[24]利用某高速公路特征断面长大下坡的实测数据，得到该路段货车速度的分布特性，并对现有的模型进行误差分析，最后修正得到有效性较高的预测模型。根据特征断面速度得到的连续长大下坡路段运行速度预测模型，见式（3）。

式中：vtruck为大货车的运行速度，km/h；G为路段（即车辆行驶处至坡顶）平均纵坡，（°）；L为累计坡长，m。

可将该预测模型简化，见式（4）。

对现有的模型进行误差分析，根据实际交通密度值进行修正，见式（5），修正后得到有效性较高的预测模型，见式（6）。

式中：K为平均交通密度，veh/km；Q为平均流量，pcu/h；v为路段平均车速，km/h。

式中：vs为限速值，km/h。

本文定义复杂组合路段为：在一定的路线长度范围内，可能产生速度突变的单元路段存在2种或2种以上的路段。本文中的复杂组合路段包括连续下坡路段+隧道路段、弯坡路段+隧道路段、连续下坡路段+互通式立体交叉路段、弯坡路段+互通式立体交叉路段这4种。

针对连续下坡和互通式立体交叉的组合路段，一方面做好连续下坡路段相关限速措施，限速值一般为设计速度或适当提高10 km/h；另一方面通过设置预告标志提醒驾驶人在坡底存在互通式立体交叉，使得车辆能够减速，提高行车安全性。

连续下坡与隧道的组合路段，存在路基和隧道护栏衔接问题和隧道洞口存在白洞效应，车辆在连续下坡路段行驶速度较高，驾驶人在洞口容易出现制动不及时引发交通事故的安全隐患。高伟[25]采用不同方法研究连续下坡与隧道组合路段的限速值，得到的结果均以设计速度作为限速值。因此对该组合路段本文以设计速度作为限制速度基准值，并根据相邻限速路段进行调整。

根据前文分析以及相关规范[26-27]可知：当隧道的圆曲线半径值为710～1 000 m，纵坡为3%～4%时，称为弯坡与隧道组合路段。隧道路段洞口运行速度和道路线形指标关系不大，隧道内车辆行驶过程分为调整阶段、稳定阶段和恢复阶段。结合弯坡路段线形特点和隧道内光线不足的特点，从安全角度考虑，该组合路段以设计速度作为限制速度基准值。

当互通式立交主线范围圆曲线半径值为700～1 000 m，纵坡为3%～4%时，称为弯坡与互通式立交组合路段。该组合路段运行速度特征与互通式立交路段类似，对互通立交范围内的主线路段做速度预测，实验结果为不同情况下的车辆运行速度差值集中在3～8 km/h 之间。GB 5768.5—2017《道路交通标志和标线第5部分：限制速度》[23]中规定将第85%位的速度作为基准，可在该速度的基础上取上下5～10 km/h 范围内的速度值为限制速度。因此弯坡与互通式立交的组合路段参照运行速度预测模型[17]，限制速度参考值在弯坡路段的速度预测基础上进行5～8 km/h的折减。

3 限速区间优化组合

根据前文对不同路段进行了简单的划分后，应该考虑不同区间之间的重新划分、融合，即优化组合的可能性，来满足限速区间的最小长度要求。

视认距离、前置距离及心里稳定距离均是从安全角度考虑，但是在确定限速区间最小长度值时不仅要从安全角度考虑，保证效率性也是科学限速的重要因素，因此需要选择1 个表征效率的指标描述通行效率水平。

通常用交通延误、行驶时间、通行能力以及饱和度等来描述道路的通行效率水平。通行能力以及饱和度作为宏观指标，数据获取难度较大且独立性较差，交通延误与行驶时间数据获取较为容易。但行驶时间较难表征通行效率的高低，交通延误表征了车辆行驶过程中受到阻碍所损失的时间，所受到的阻碍主要包括其他车辆干扰。交通延误较低时，驾驶人受到其他车辆影响较小，交通流相对稳定，因此路段的通行效率采用交通延误表征是可取的。

3.1 限速区间优化方法

聚类分析法将样本中的相似个体按照物以类聚的方式划分。有序聚类分析法中基于划分和层次的分析法适用于存在层级关系的样本数据，与限速区段的划分特点相适应，因此本文选用此聚类方法对高速公路的限速区间进行优化。

结合高速公路特点及限速路段设置原则，根据第2节中划分区间的限速值进行区间的初步分段限速。本文所采用的优化限速区间的有序聚类分析法，可以在不打乱次序的条件下按照一定原则对区间进行合并优化。假设高速公路全线路段划分N个限速路段，并对每个限速路段进行编号，见图4，令vi表示第i个限速路段的限制速度值，li表示第i个限速路段的区间长度（i=1,2,…,N）。

图4 限速路段划分示意图Fig.4 Schematic diagram of speed limit road segmentation

本文区间划分优化方法存在以下假设：①限速区间内车辆均以限制速度匀速行驶；②限速区间如果发生拥堵能迅速疏散；③车辆在全线路段服从均匀分布；④不考虑驾驶人对限速区间措施的服从概率。

根据以上假设，本文限速区间划分原理为：由前文提出的限速区间划分及限速值初步分段限速，之后根据限速区间最小长度判断各个路段是否需要优化组合，对不满足要求的路段通过与相邻路段直接组合或分割相邻路段重新组合构成新的限速区间，新限速区间应满足长度要求并且交通延误最小，并对优化后的新限速区间采用限速区限速的方式。

分割相邻路段的具体过程如下，其具体步骤见图5，该过程假设第i个区间段长度不满足要求。

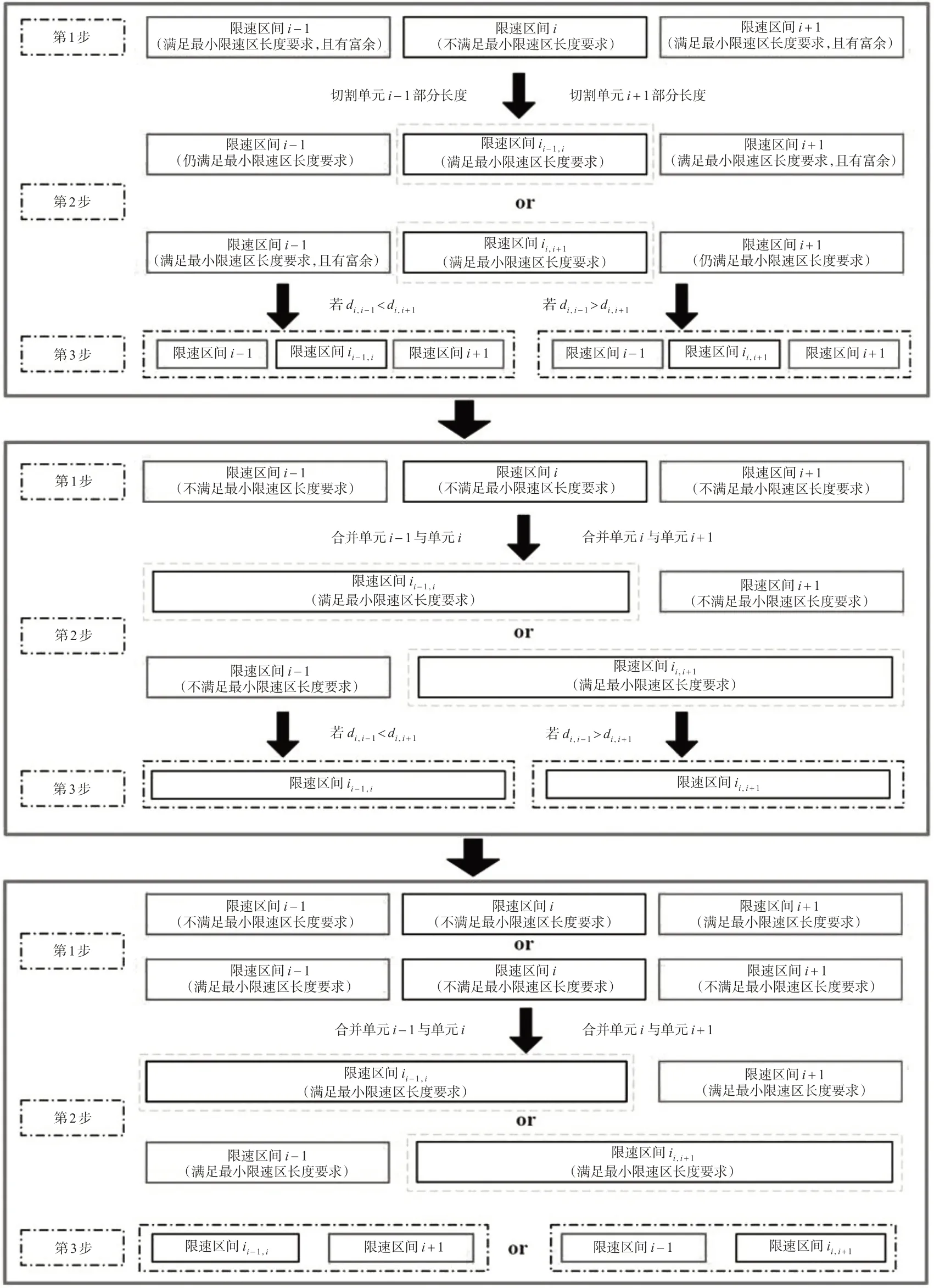
图5 限速路段划分优化方法流程图Fig.5 Flow chart of optimization method for speed limit road segmentation

1）当相邻限速区间均满足长度要求。分割相邻限速区间i-1 和i+1，当分割后i-1 限速区间依然满足最小长度要求时，将分割的单元与限速区间i合并为新的限速区间ii-1,i，计算交通延误值为di-1,i；同理当分割后i+1限速区间满足最小长度要求时，进行同样操作，新的限速区间为ii,i+1，交通延误值为di,i+1。比较di-1,i和di,i+1，选择交通延误较小者作为最终的划分区间。在保证相邻限速区间分割后长度满足要求的情况下形成的新限速区间依然无法满足最小长度要求时，同时分割相邻限速区间i-1和i+1，分割方法同上，以交通延误最小作为指标选择最终限速区间。

2）当相邻限速区间均不满足长度要求。先将限速区间i-1 与限速区间i合并为新的限速区间ii-1,i，计算交通延误值di-1,i；同理合并限速区间i和i+1，新的限速区间为ii,i+1，交通延误值为di,i+1。比较di-1,i和di,i+1，选择交通延误较小者作为最终的划分区间。若合并后的区间仍不满足长度要求，将合并后的区间再假设为区间i，进行相同的区间分割方法。

3）当相邻限速区间中1个满足长度需求。当限速区间i-1 长度不满足要求，合并限速区间i和i-1，新的限速区间为ii-1,i；当限速区间i+1长度不满足要求，合并限速区间i和i+1，新的限速区间为ii,i+1。

3.2 限速区间优化方法有效性分析

当完成高速公路限速区间划分及其优化组合后，需对其进行优化前后的指标对比分析来验证所提出方法的有效性。在分析指标的选择上，本文同样从安全以及效率2个方面来进行。目前研究中主要的安全评价指标为：交通事故率、冲突率，速度离散性以及车头间距与车头时距；效率评价指标为：交通延误、车辆行驶时间、道路通行能力和饱和度。根据指标的适用性及代表性，具体选取结果见表5。

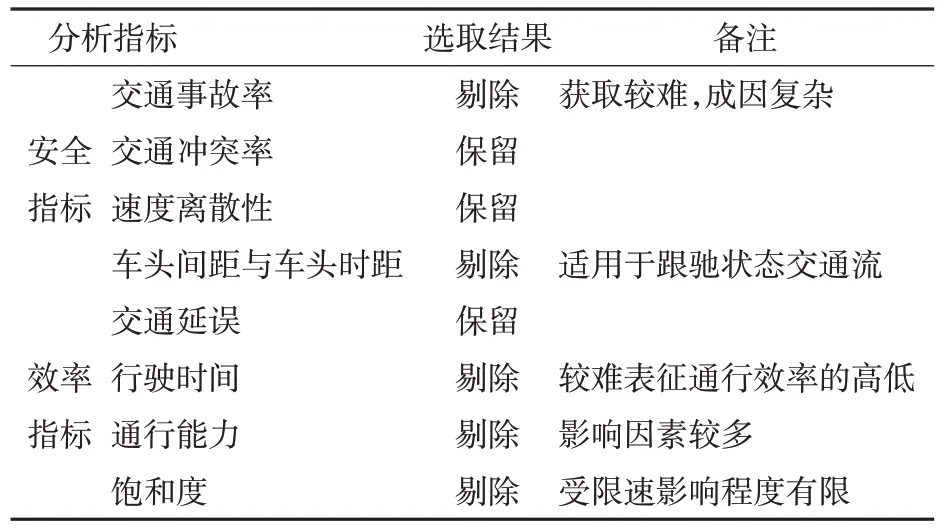
表5 分析指标选取Tab.5 Analysis index selection

因此，在交通量一定的前提下，根据各个指标间的关系建立了对应的交通安全以及效率评价指标模型，由于选取的安全评价指标与交通安全间的关系均为负相关，建立式（7）；根据所选效率评价指标与交通效率间的正、负相关关系，建立式（8）。其中，速度离散性指标根据郝亮[28]的相关成果，以相对速度差来表征路段的速度离散程度，其定义见式（9）。

式中：f安为交通安全评价指标；VR85-15为相对速度差，km/h；Q为路段交通量，pcu/h；TC为交通冲突数，起；f效为交通效率评价指标；Vˉ为路段平均速度，km/h；t为路段行程时间，s；d为路段交通延误，s；ρt为大型车比例，%；V85为路段第85%车速，km/h；V15为路段第15%车速，km/h。

当VR85-15大于20 km/h 时，应考虑按JTG/T 3381—02—2020《公路限速标志设计规范》[29]设置必要的过渡段。

4 实例分析

用于实例分析的高速公路应具有较长的里程数、具有一定的复杂组合路段和设计指标不宜过高几个特点，因此本次分析选用的高速为我国西南某山区高速公路，其设计指标见表6。

表6 设计指标参数Tab.6 Design index parameters

虽然该高速公路未突破规范规定要求[26]，但是在实际运营过程中道路上的运行速度达到100 km/h，某些路段运行速度甚至达到了120 km/h，因此指标采用存在一定的安全隐患。统计该高速公路2017—2019 年共计309 起交通事故，发现事故形态主要是制动不及时，车辆撞向路侧和中分带护栏，主要原因是车辆超速导致的。

经过实地调研，该高速公路限速统计见表7。

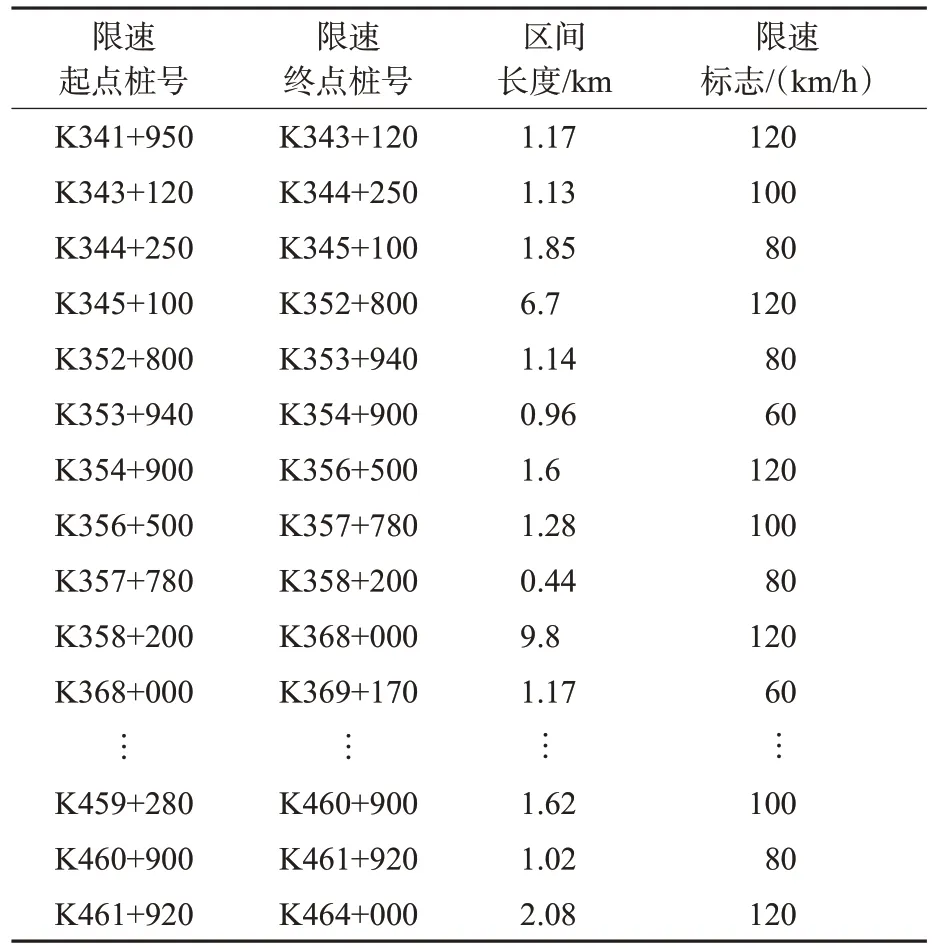
表7 限速统计表（部分）Tab.7 Speed limit statistics table(part)

全线共设计44个限速区间，一方面制定限速方案时没有考虑限速区间长度的问题；另一方面限速区间过于密集，影响驾驶人驾驶体验，也增加了行车操作难度。因此该高速公路事故频发的原因除了自身建设条件有限以外，限速方案的不合理也是重要原因。

根据所提出的模型对该山区高速限速路段进行梳理及优化，对比相邻区间组合前后的交通延误值重新对区间进行划分，优化后的限速区间见表8。

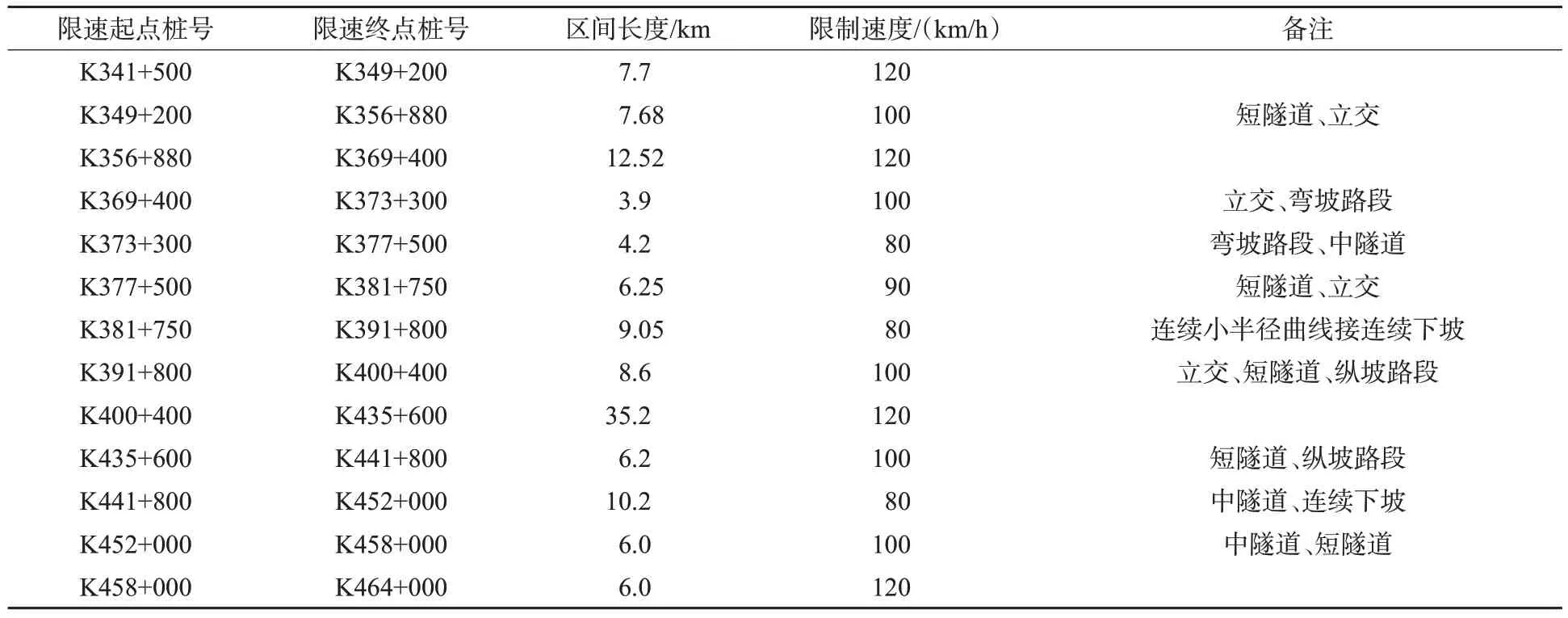
表8 优化后的限速区间Tab.8 Optimized speed limit section

应用VISSIM 仿真软件对该高速公路限速方案进行仿真模拟，按照1∶1 比例尺进行建模，对该高速公路3%以上的纵坡进行了修正。并将限制速度作为期望速度，在路段的起点、中间位置及终点设置数据采集点，并针对较长区间路段及线形指标变化较大的路段进行适当加密。仿真参数设置为：车道宽度3.75 m，单向4 车道，路段长度123 km。仿真车辆参数见表9，数据输出起始节点选择仿真的第一辆车到达路段终点时刻，仿真1 h 后结束仿真试验。

表9 仿真车辆参数Tab.9 Simulation vehicle parameters

对该高速公路进行实地调研后，选取7 个特征断面，测得其平均小时交通量约为1 082 辆/h，见表10。选择小客车、大货车作为代表车型，大型车比例为17.47%，其余车型均已根据JTG D20—2017《公路路线设计规范》[26]中的车辆折算系数进行换算。

表10 实测小时交通量统计Tab.10 Measured hourly traffic volume statistics单位：辆/h

运用VISSIM 进行仿真模拟，其操作界面、仿真参数设置见图6。

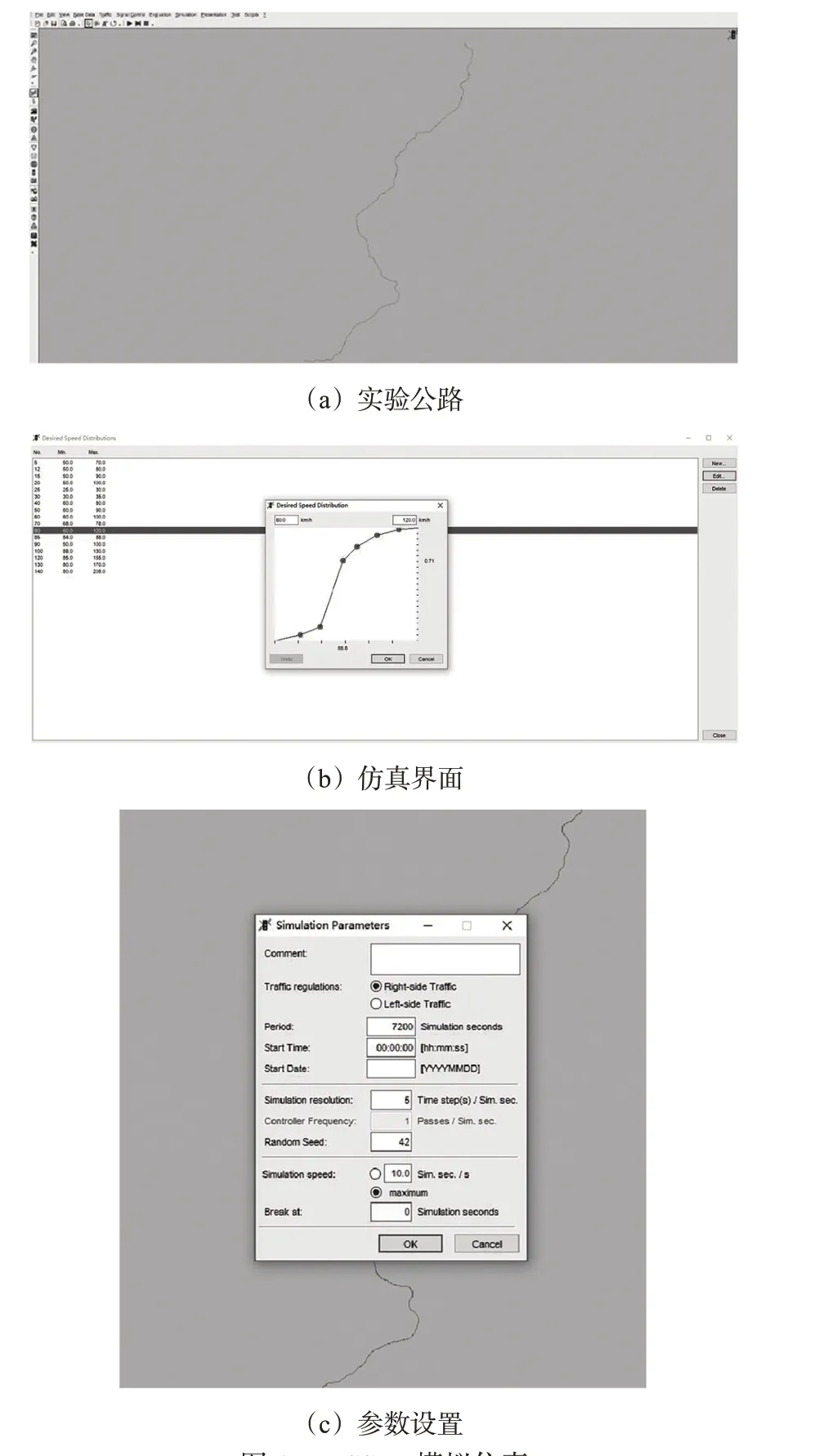
图6 VISSIM模拟仿真Fig.6 The VISSIM simulation

分析VISSIM输出的数据，并把车辆行驶轨迹输出后利用SSAM 交通冲突安全分析软件处理，原限速方案的路段仿真及交通冲突分析结果见图7。

图7 原限速方案Fig.7 Original speed limit scheme

优化后方案的路段仿真及交通冲突分析具体结果见图8和表11。

表11 限速方案对比Tab.11 Speed limit plan comparison

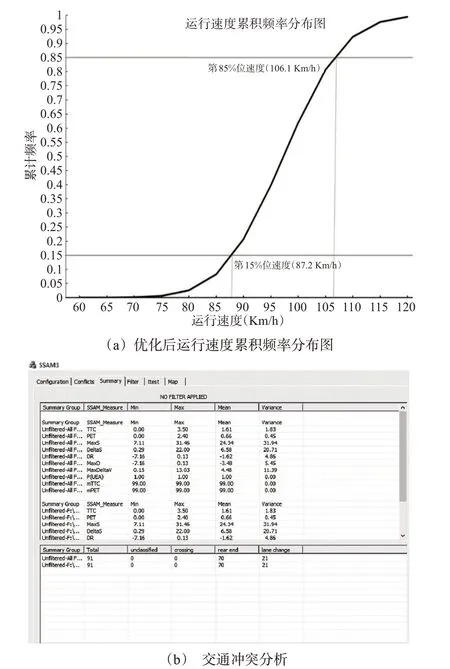
图8 优化后方案Fig.8 Optimized scheme

根据前文提出的有效性评价模型，原限速方案的安全评价模型参数及效率评价模型参数为

优化后方案的安全评价模型参数及效率评价模型参数为

安全评价模型数值越小越安全，而效率评价模型数值越大效率越高。分析可知：安全评价模型参数值优化后比原限速方案降低了约29.49%，效率评价评价模型参数值优化后比原限速方案提高了约21.90%。

本文以是否造成路段行驶速度突变作为划分依据，将路段分为不同属性的限速单元，采用有序聚类方法对其限速段进行聚类整合，并基于交通延误最小方法进行限速单元的优化。通过对比分析各指标，可得优化后该高速行程时间变短，交通延误减少并且平均速度提高，这表明优化后的高速公路车辆行驶的整体通行效率提高；优化后该高速相对速度差变小，这表明优化后的高速公路整体的速度连续性得到提高，速度离散性减小；优化后交通冲突数变小，其中换道冲突数大致没变，追尾冲突数大大减少，这表明优化后的高速公路整体的安全性得到提升。综上所述，优化后的高速公路无论是安全性还是通行效率均得到增强，这表明所提出的模型方法是可行有效的。

5 结束语

针对目前高速公路限速标准存在的问题，分别对限速区间长度取值、限制速度确定以及限速区间划分优化进行研究，综合提出了一套高速公路限速区间确定方法。

1）通过对标志视认距离、标志设置前置距离以及驾驶人稳定行驶距离进行分析，综合确定了高速公路限速区间长度的最小值；以行驶速度易发生突变为标准对路段进行划分，并确定各路段的限速值；基于有序聚类分析法结合最小交通延误值重组限速区间，优化了各限速区间的组合。

2）根据我国某山区高速限速方案，采用本文的模型方法进行优化，利用VISSIM 软件仿真分析，经对比后发现安全方面优化后模型参数值降低了约29.49%，效率方面优化后模型参数值提高了约21.90%，结合各指标变化表明经过优化后高速公路整体的安全性和通行效率均得到提高。

3）本文选择小客车、大货车作为代表车型进行研究，用VISSIM对该高速公路限速方案进行仿真模拟，模拟的车辆行驶轨迹难免会与实际情况有出入。后续应进一步分析不同车型的行驶特征，深入研究高速公路限速区间长度和区间的划分的优化方法。

本文建立的高速公路限速区间确定方法，优化了在制定限速区间长度以及限速区间划分方面相关问题，为我国高速公路限速值制定不科学、限速区间划分不合理等问题提供了参考。