理解：从“发现”到“迁移”的脚手架——例谈促进学生理解的教学设计策略

周晓萍

在日常教学中，我们经常会有这样的体验，课堂上学生似乎对所学知识已经掌握得比较好了，但课后练习效果却并不理想。这一现象说明课堂上“掌握得较好”是个假象，那只是一种浅层的“发现”和模仿而已，学生对所学知识并未真正理解、内化。教学中教师要努力为学生搭建“理解”的脚手架，引导他们将所学知识技能迁移到新的问题情境中，从而解决实际问题。

一、优化方式，举一反三

一次单元测试中，有这样一道题：“一支篮球队三场比赛的平均得分为105分，要使平均分达到120分，第四场应得（ ）分。”班上47名学生，仅有28名学生解答正确，正确率仅59.6%。这类题型在测试前学生已经练习过，已总结出这类题的数量关系是“第四场得分=四场总分－三场总分”。单元测试中正确率依然偏低意味着有相当一部分学生对这一数量关系的理解不到位或者根本没理解。于是笔者及时调整了教学策略，优化了讲评方式——

第一层次：让解答正确的学生阐释“120×4－105×3”这一算式的每一步分别表示什么，唤起大部分学生对解答该题基本数量关系的记忆。

第二层次：引导学生用画图的形式换个角度去理解（如图1）。

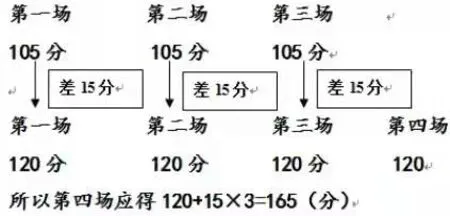
图1

第三层次：改变该题的应用情境，编题：“吴××（班上的一名学生）若在最近的单元测试中语文和数学两门平均分是70分，如果他想让语数英三门的平均成绩达到75分，那么他在接下来的英语测试中需要获得（ ）分？”包括吴同学在内的全班绝大部分学生都正确解答出了这道题，并且大部分学生用的是第二种解题思路。

第四层次：你能编一道类似的考题吗？

针对该教学环节进行的三个方面的优化，有效促进了学生对知识点的理解，提高了他们的举一反三的能力。

一是转换角色，以学生能理解的方式解析

此类题中的数量关系对于大部分学生而言是比较难理解的，于是，当教师站在学生的角度去思考问题，以边画图边解析的比较直观的方式去引导学生分析数量关系时，他们一下子就明白了。理解了解法二的思路，又促进他们进一步去理解解法一的思路，于是数量与数量之间的关系就明晰了，理解也就真正达成了。

二是改变应用情境，用学生能理解的内容铺陈

第三层次以学生身边的实际例子即吴姓同学作为题材引入题目，则一下子打开了学生思维的闸门，他们很容易地把数学模型从题目的细节中抽取出来，从而利用平均数的知识顺利地解答该题。这也再次表明，紧密联系学生的生活实际优选教学内容，是促进学生理解的重要策略之一。

三是鼓励参与，将学生卷入深度理解的场域

在解决问题的教学中，为帮助学生正确理解数量关系，改编数据、情节、问题结构等，以题组形式呈现是常用的方法，本环节也是通过改编不断强化学生对一类题的基本数量关系的理解。特别重要的是，改编的主体由教师的示范引领转入学生的全员参与，在那一刻，会编题、能解答出同学所出的题既是对学生知识掌握程度的再度考查，也是一次学法指导的良机。这一形式本身也是促进他们深度理解的又一手段，“举一反三”“变中求不变”等数学思想方法得以无痕渗透。

二、深化内容，凸显本质

有这样一道找规律填数题：

用左边的“十”字框在表中框出5个数，先算算这5个数的和，再想想算出的和与中间这个数有什么关系。如果5个数的和为105，请在“十”字框中写出这5个数（如图2）。

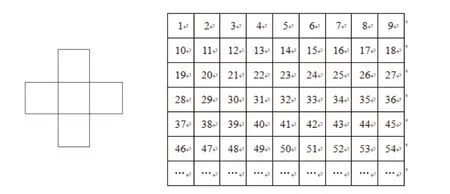
图2

初次教学该内容时，分两步走——

第一步，举例→发现规律。引导学生用“十”字框任意框选一组数，通过几组数的计算反馈，组织交流时发现“十”字框中五个数的和总是中间那个数的5倍，并且未发现任何反例。因此，如果5个数的和为105，则可以用105÷5求出中间的数为21，继而从表中可以找出另外四个数分别是20、22、12、30。

第二步，巩固→初步建模。在学生初步发现规律后，给出了两道模仿练习题：如果5个数的和为120，这5个数分别是多少？如果5个数的和为65呢？由于这两题的答案都可以从表中找到，此时的巩固还未对学生的思维形成挑战。事实上，绝大部分学生都是先用总和除以5求出中间的数之后，再到表中去框出其他四个数的。于是出示如下的题：如果框出的5个数的和是375呢？你还能在“十”字框中填出这5个数吗？该题的答案是无法直接从表中简单找到的，此时学生不得不丢开表格，进一步探究“十”字框中5个数之间的本质关系。通过深入探究和思考，他们发现“十”字框中横向排列的三个数每两数之间相差1，而纵向排列的三个数每两数之间相差9。至此，5个数的相互关系基本理清。

然而，当学生在家庭作业中遇到下题时（如图3），却有75%的学生出现了错误，他们在“十”字框中是这样填写的：

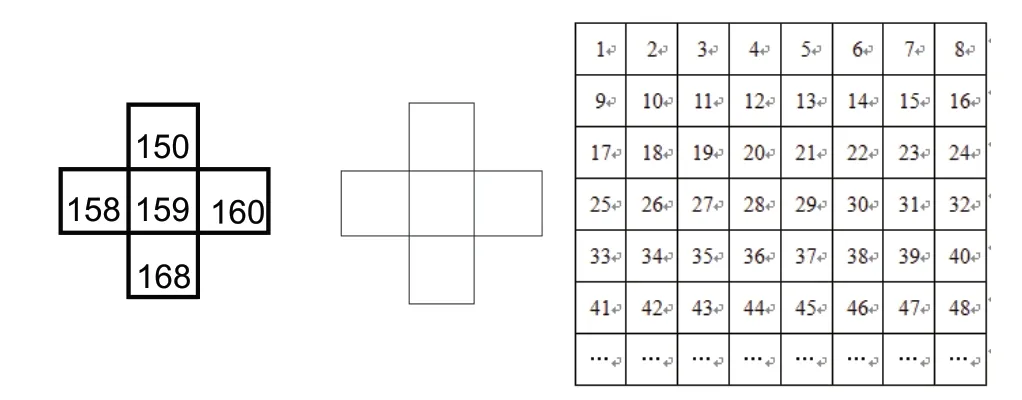
图3

用左边的“十”字框在表中框出5个数，先算算这5个数的和，再想想算出的和与中间一个数有什么关系。如果5个数的和为795，你能在左边的“十”字框中写出这5个数吗？

换了一个数表就频频出错，意味着学生对规律的认识不深刻，一旦情境发生变化，迁移便无法顺利完成。能否将知识迁移到新的情境中去，是 “理解” 是否真正达成的表征。基于“理解”来思考本题的教学，又该如何来设计呢？

在原有的两个环节基础上再增加两个环节：

第三步：变式→凸显本质。出示家庭作业中的那道题，引导学生发现，每行9个数变为每行8个数后，上下两行间相对应的两个数的差也随之发生了改变，因此，“十”字框中的5个数不仅会随着中间那个数的变动而变动，也会随着数表中数的排列特征而改变。

第四步：理解→迁移应用。再次聚焦问题，追问：从前面的两例中我们发现，“十”字框中纵向排列的三个数之间的关系会随着每行数的个数的变化而变化，而横向排列的三个数每两数之间的差却都是1，那么，横向排列的数差只能是1吗？你能自己设计一个数表，给大家提供一个继续深入探究的素材吗？

增加的环节三通过聚焦问题、反馈、诊断性评价等，把学生的潜在误解揭示出来，“逼”着他们提前暴露出认知上的问题。环节四则帮助学生揭示了他们的问题、疑问、假设，引导他们深入地探究该题基本框架之外的未知领域，逼近所研究问题的本质属性，从而帮助学生搭建起从“发现”到“迁移”的“脚手架”，赋予他们一种高阶思维，提高他们在灵活变化中解决实际问题的能力。