广州南沙某桥头路基处理方案对比及其工后沉降分析

周文辉，肖 宁，占 辉，贺佐跃

(1.广东省交通规划设计研究院集团股份有限公司，广州 510507；2.广州市南沙新区明珠湾开发建设管理局，广州 511466)

桥头路基差异沉降是导致跳车的主要原因，严重影响了行车舒适度和安全性[1]。由于软土工程性质的特殊性，软土区的桥头路基处理更具挑战性。常用的软土地基处理措施包括堆载/真空预压、水泥搅拌桩、高压旋喷桩、CFG桩和管桩等[2-4]，但这些处理并不完全适用于桥头路基。

规范规定：桥头路基工后沉降不应大于10 cm，因此在进行桥头路基处理时，应选取合理的处理措施。苏谦等[5]分析了泡沫轻质土进行桥头路基换填的效果和经济性。高志伟等[6]分析了采用复合地基处理后，路面结构对车辆行驶振动特性的影响作用。吴勇强等[7]对环杭州湾地区厚覆盖层桥头路基真空联合强夯、旋喷桩及轻质土换填等不同处理方法的效果进行了详细分析。张军等[8]通过现场试验和数值模拟，对路桥过渡段路堤加筋的处理效果进行了分析。贾亮等[9]进行了过渡段工后沉降监测试验研究，得到了沉降随时间和空间的变化规律。邓露等[10]确定了过渡段容许台阶高度，并提出了更合理的高度控制标准。郑俊杰等[11]通过路桥过渡段桩承式加筋路堤现场试验研究，发现在桥台附近减载作用明显，并随距桥台距离增加而逐渐减弱。羊晔等[12]通过研究过渡段差异沉降控制标准，得到不同路堤高度时路面纵坡与差异沉降的关系式。沈水龙等[13]通过分析3种常用的过渡段地基处理方法，介绍了缓解跳车现象的设计施工CA工法。这些研究均只研究了桥头路基处理的某一方面，而在实际工程中，由于土体性质的显著差异性，这些研究的应用受到限制[14-17]。此外，对于高等级道路，桥头路基工后沉降的控制要求较高，相关处理措施还需进一步研究[18-20]。

本文针对广州市南沙区某工程项目，通过规范法和数值分析两种计算手段，对堆载(等载)预压+塑料排水板+管桩、直接管桩这两种桥头路基处理手段及其对工后沉降的影响进行对比分析，以期为该地区的实际工程提供参考。

1 工程概况

广州市南沙区明珠湾区横沥岛尖路网工程地处南亚热带，海拔低，气候类型属于亚热带季风区，夏长冬短，湿润多雨。该区域内水系发达、河涌密布，具有深厚的软弱土层，如图1所示。桥头路段路基高5 m，顶宽20 m，路肩坡度为1∶1.5，采用堆载(等载)预压+塑料排水板+管桩复合地基处理(方案1)，即先进行等载预压、再进行管桩处理，对比方案为直接进行管桩复合地基处理(方案2)。这两种方案的路肩均采用水泥搅拌桩处理。管桩外径0.4 m、壁厚0.1 m，桩长31 m，间距2.2 m，正方形分布。水泥土搅拌桩直径0.5 m，桩长20 m，间距1.2 m，三角形分布。塑料排水板为C型，截面尺寸为100 mm×4.5 mm，等效直径为0.067 m，长25 m，与管桩、水泥土搅拌桩相间分布。这两种处理方案的具体步骤如下。

图1 工程区域卫星地形图

1)方案1：堆载预压+塑料排水板+管桩。施工步骤大致为塑料排水板→分层堆载→等载预压→卸载→管桩→路堤→运营。其中，管桩仅在路基顶宽范围内施工，两侧路肩采用水泥土搅拌桩处理。

2)方案2：管桩。施工步骤大致为管桩→路堤→运营。同样的，管桩仅在路基顶宽范围内施工，两侧路肩采用水泥土搅拌桩处理。土层、既有路基、管桩和水泥搅拌桩的主要物理、力学参数分别见表1、表2。土层厚度按照表1层序依次为1、15、11.5、4.5、5 m。

表1 土层主要物理、力学参数

表2 既有路基和桩的主要物理、力学参数

2 计算条件

方案1在规范法岩土中的实现方法为：先计算堆载预压，再以计算结果作为管桩计算的初始条件，将这两个步骤的位移结果进行叠加。方案2在规范法岩土中可直接进行计算。为考虑分层堆载时间、等载预压时间及路堤再加载时间等因素的影响，上述两种处理方案的计算条件见表3。

3 规范法计算结果分析

路基底部中点沉降随时间的变化规律如图2所示，其中图例数字与表3中的序号一致。由图可以看出，在上述两种方案中，该点沉降随时间均表现出先快速增加、再趋于稳定的变化规律。方案1中，该点沉降均达到0.7 m以上；分层堆载时间越长、或等载预压时间越长，该点稳定沉降均越大；路堤再加载时间对该点沉降随时间变化规律几乎无影响。此外，相较于方案1，方案2中该点沉降很小，最大仅约为3 mm。

表3 计算条件 单位：月

图2 时间vs沉降(规范法)

路基底部中点沉降速率随时间的变化规律如图3所示，其中图例数字与表3中的序号一致。由图可以看出，在上述两种方案中，该点沉降速率随时间总体上均表现出逐渐减小并趋于稳定的变化规律，但在堆载或填土施加时刻，沉降速率会表现出突变。方案1中，该点沉降速率最大值均达到3 mm/d以上；分层堆载时间越长或等载预压时间越长，该点稳定沉降速率均越大；路堤再加载时间对该点沉降随速率时间变化规律几乎无影响。此外，相较于方案1，方案2中该点沉降速率很小，最大仅约为0.33 mm/d。

图3 时间vs沉降速率(规范法)

表3中各序号的工后沉降如图4所示。由图4可以看出，无论采用何种方案或计算条件，计算得到的工后沉降均为0。规范规定：桥头路基的工后沉降不应大于10 cm，但实际工程中几乎不会出现工后沉降为0的沉降。这与规范法岩土的计算方法有关，也说明了该软件在进行分步计算工况时存在一定缺陷。

图4 工后沉降(规范法)

4 数值计算结果分析

由前文可知，规范法岩土在进行分步计算工况时存在缺陷，而数值方法可有效地解决分步工况问题，在几何建模方面也有充分的自由，在实际工程中的应用也越来越广泛。Midas GTS有限元数值模型如图5所示，模型长235 m、宽100 m，管桩、水泥搅拌桩及塑料排水板模型分别以紫色、绿色及灰色表示，如图6所示。对于方案1，管桩、水泥搅拌桩及塑料排水板均激活；对于方案2，仅激活管桩。

图5 数值模型(整体)

图6 数值模型(管桩、水泥搅拌桩和塑料排水板)

方案1共有10个模拟阶段，分别为：①初始静力平衡，位移清零；②分层堆载1，填土高度2 m；③分层堆载2，填土高度2 m；④分层堆载3，填土高度1 m；⑤静置期1，等载预压时间；⑥撤除塑料排水板；⑦堆载卸载；⑧管桩、水泥土搅拌桩施工；⑨路基填土加载；⑩静置期2，180月，同时在路基顶部施加20 kPa荷载。

方案2共有7个模拟阶段，分别为：①初始静力平衡，位移清零；②管桩、水泥土搅拌桩施工；③路基填土1，填土高度2 m；④路基填土2，填土高度2 m；⑤路基填土3，填土高度1 m；⑥工后基准期，1月；⑦静置期2，180月，同时在路基顶部施加20 kPa荷载。

路基底部中点沉降随时间的变化规律如图7所示，其中图例数字与表3中的序号一致。由图7可以看出，方案1中该点沉降随施工阶段会波动，且稳定沉降均达到约0.37 m；分层堆载时间、等载预压时间及堤再加载时间对该点沉降大小的影响总体较小。此外，相较于方案1，方案2中该点沉降较小，最大仅约为0.12 m。

图7 时间vs沉降(数值分析)

路基底部中点沉降速率随时间的变化规律如图8所示，其中图例数字与表3中的序号一致。由图8可以看出，与规范法计算结果类似，在上述两种方案中，该点沉降速率均在堆载或填土施加时刻表现出突变。方案1、2的沉降速率最大值均达到15 mm/d以上；分层堆载时间越长、或等载预压时间越长，该点稳定沉降速率均越大；路堤再加载时间对该点沉降随速率时间变化规律几乎无影响。

图8 时间vs沉降速率(数值分析)

表3中各序号的工后沉降如图9所示。工后沉降为路基填筑完成至180月期间内的沉降。由图9可以看出，总的来说，相较于方案1，方案2的工后沉降要大5 mm左右。分层堆载时间、等载预压时间及路堤再加载时间等，对方案1工后沉降的影响总体上很小；路基填土时间增加可降低方案2的工后沉降。这里计算得到的工后沉降均位于1～2 cm，远小于规范要求的10 cm。然而，计算结果仍表明方案1更能降低工后沉降。此外，还表明数值计算能够较好地解决分步计算工况问题。

图9 工后沉降(数值分析)

路基中线沿深度方向的沉降如图10所示，其中图例数字与表3中的序号一致。由图10可以看出，方案1最大沉降发生在深度为0处，达到约0.39 m；分层堆载时间、等载预压时间及路堤再加载时间等对路基中线沿深度方向的沉降可以忽略不计。相较于方案1，方案2时路基中线沿深度方向的沉降很小，仅约为0.15 m，且在该方向上的变化也很小。

图10 中线沿深度方向沉降(数值分析)

若以桩施工完成时间为基准，可得到桩施工完成至模拟结束期间内发生的沉降，即净沉降如图11所示。由图11可以看出，同样的，分层堆载时间、等载预压时间及路堤再加载时间等对路基中线沿深度方向的沉降可以忽略不计。在沿深度方向上的沉降增量，两种方案几乎相同个，均为5 mm。然而，方案1的最大沉降不超过8.5 cm，而方案2的沉降均超过10.4 cm。这表明经过堆载预压后，土层的固结度显著增加，有效减小了土层的后续沉降。

图11 中线沿深度方向净沉降(数值分析)

由前文可知，软弱土层的固结程度与桥头路基工后沉降密切相关，固结程度大小会显著影响土层的力学性质。因此，这里将以表3中序号1的计算条件为基准，对②5淤泥质粉质黏土的力学参数，即黏聚力、内摩擦角和压缩模量等对工后沉降的影响进行分析。

工后沉降随黏聚力的变化规律如图12所示，黏聚力分别为3、5.5、8 kPa，其他参数均保持不变。由图12可以看出，总的来说，随黏聚力增加，方案1的工后沉降逐渐增加，而方案2的工后沉降逐渐减小，但增加或减小幅度较小。相较于方案1，在本文黏聚力分析范围内，方案2的工后沉降仍然大5 mm左右。计算结果表明：当在管桩施工前进行堆载预压时，软弱层黏聚力越大，工后沉降也越大；而无堆载预压时，黏聚力越大，工后沉降略小。

图12 黏聚力vs工后沉降

工后沉降随内摩擦角的变化规律如图13所示，内摩擦角分别为3°、5.5°和8°，其他参数均保持不变。由图13可以看出，总的来说，随内摩擦角增加，方案1、2的工后沉降均减小，但减小幅度较小。相较于方案1，在本文内摩擦角分析范围内，方案2的工后沉降仍然大5 mm左右。计算结果表明：当在管桩施工前进行堆载预压时，软弱层内摩擦角越大，工后沉降也越小；而无堆载预压时，内摩擦角越大，工后沉降则越小。同时也表明可采取适当的地基处理措施，提高土层的内摩擦角，降低工后沉降。对比本文分析的两种方案，相较于方案2，方案1增加了堆载预压，因此工后沉降要更小。

图13 内摩擦角vs工后沉降

工后沉降随压缩模量的变化规律如图14所示，压缩模量分别为0.25、1、2.6 MPa，其他参数均保持不变。由图14可以看出，随压缩模量增加，方案1的工后沉降逐渐增加，相较于压缩模量为0.25 MPa时，压缩模量为2.6 MPa时的工后沉降要大8 mm左右。而方案1的工后沉降随压缩模量逐渐减小，但减小幅度较小。压缩模量越小，两种方案的工后沉降差值越大，当压缩模量为0.25 MPa时，工后沉降差值达到约14 mm。这表明：当在管桩施工前进行堆载预压时，较小的压缩模量能够得到较小的工后沉降。

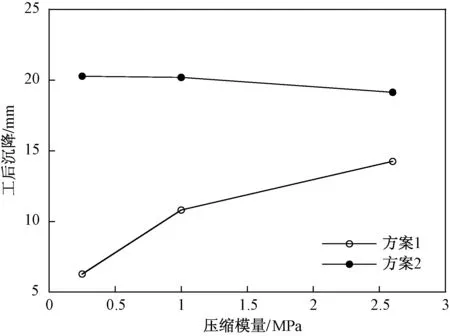
图14 压缩模量vs工后沉降

需要注意的是，黏聚力、内摩擦角和压缩模量等力学参数的减小，说明土层性质越差，总沉降量也越大。但这些力学参数与工后沉降之间的关系，并不是简单的单调关系。这与路基的处理方式有关。

1)对于方案1，由于在管桩施工前进行了堆载预压处理，黏聚力和压缩模量增加会导致工后沉降增加，而内摩擦角与之相反。堆载预压能显著提高软弱土层的固结度，但当黏聚力和压缩模量较大时，尽管总沉降会更小，但同等堆载作用下施工期的沉降作用相对减弱，导致工后沉降相对增加。而内摩擦角施工期的沉降作用仍相对较强，导致工后沉降相对减小。

2)对于方案2，尽管黏聚力、内摩擦角和压缩模量增加均导致工后沉降减小，但由于在管桩施工前未进行堆载预压处理，因而减小幅度总体上较小。

此外，通过规范法和数值法的对比分析表明：当采用管桩复合地基处理时，规范法的工后沉降均为0，明显与实际工程不符。若仍采用规范法，将导致设计偏于不安全，而数值法能有效避免这种情况。当土质发生变化时，数值法得到的工后沉降也随之发生变化，并能够根据工后沉降进行设计方案的调整，而规范法无法做到这一点。

5 结论

1)规范法仅能考虑分层堆载时间和等载预压时间的影响，未能考虑路堤再加载时间的影响，无论采用何种方案或计算条件，计算得到的工后沉降均为0。这与实际不符，说明该软件在进行分步工况及工后沉降计算时存在缺陷。

2)数值分析能够同时考虑分层堆载时间、等载预压时间及路堤再加载时间的影响，也能够较好地解决分步计算工况问题。方案2的工后沉降要大，表明经过堆载预压后，土层的固结度显著增加，有效减小了土层的后续沉降。

3)对于方案1，随②5淤泥质粉质黏土的黏聚力或压缩模量增加，工后沉降均逐渐增加，而内摩擦的影响与之相反；对于方案2，随黏聚力、内摩擦角或压缩模量增加，工后沉降均逐渐减小，但减小幅度较小。

本文仅对两种设计方案进行了对比分析，后续相关的监测工作在施工完成后逐步开展，但本文分析结果仍为该地区其他类似实际工程的设计和施工提供了重要参考。