微分几何学在中国的早期发展及其启示——基于学术谱系视角

陈克胜

(西北大学科学史高等研究院，西安 710127)

建设数学强国目标已成为中国社会各界共同的期盼，其标志性的表现主要有：中国数学家敢于和能够挑战一些重大的数学问题、在现代数学发展的若干分支中有新的突破、有原创性的成果等。但是数学是一门累积性很强的科学，一些重要成果的突破往往需要经历一段较长时间的前期积淀过程，需要有若干代甚至几十代数学家携起手来共同奋斗、前仆后继，如哥德巴赫猜想的证明等，这样便容易形成数学家学术谱系。所谓数学家学术谱系，是指由数学学术传承关系(包括师承关系在内)关联在一起的、不同代际的数学家所组成的学术群体，它是数学学术传统的载体。由此，研究数学家学术谱系成为一种必然，其研究价值最突出的是：可以探索数学发展规律和数学家成长规律等。从某种程度上来说，中国现代数学家学术谱系研究对于当前中国探索走向数学强国之路具有重要的借鉴意义和现实价值。

微分几何学是由国外移植到中国最早的现代数学分支之一，姜立夫是将微分几何学引入到中国的第一人。此后，中国历代微分几何学家们在进行学术研究的同时，都非常重视微分几何学方向的人才培养，由此比较早地形成了具有一定学术水平和规模的中国学术群体，某些成果也已达到世界一流的水平。除此之外，人们更感兴趣的是：微分几何学在中国早期的发展中取得成功的深层次原因是什么？是否存在某些规律？其规律又是怎样的？对于当前中国建设数学强国有何启示？

关于微分几何学在中国的研究已相当多，大体可以分为三类：第一类侧重于微分几何学家个人的学术经历和成就，如程民德主编的《中国现代数学家传》[1]，张洪光的《二十世纪伟大的几何学家陈省身》[2]。第二类侧重于微分几何学发展内史，如苏步青的《几何学》[3](与严志达合写)、《一般空间几何学的新发展》[4]和《十年来中国微分几何的发展》[5]，美国费兹吉拉尔德(A. Fitzgrald)和麦克莱因(S. MacLane)的《纯粹和应用数学在中国》(PureandAppliedMathematicsinthePeople’sRepublicofChina)[6]。第三类是侧重于将中国在微分几何学的工作置于整个微分几何学发展中，如日本数学家窪田忠彦(T. Kubota，1885—1952)的《仿射平面理论的若干评论》(EinigeBemerkerkungenzurAffinflachenTheorie)[7]。上述成果是从不同角度进行研究，主要回答“是什么”的问题，但是很少涉及微分几何学在中国所蕴涵的某些发展规律。值得关注的是，国内研究者开始尝试从学术谱系的角度来研究中国部分微分几何学家及其成就，如李大潜和华宣积的《苏步青与中国微分几何学派》[8]，但仅局限于中国某个学术群体。本文将基于学术谱系研究的视角来梳理早期有影响的中国部分微分几何学家的师承关系及其合作者关系，由此探索中国微分几何学家的学术成长及其人才培养规律；探讨微分几何学的中国学术传统，由此探索微分几何学在中国的发展规律。

为了研究的需要，本文选取了程民德主编的《中国现代数学家传》和卢嘉锡主编的《中国现代科学家传记》[9]中入传的微分几何学家或有关的数学家，即本文考察的对象主要是在民国时期成长起来的中国部分微分几何学家。通过对这些已入传的微分几何学家开展学术谱系研究，基本可以达到所要求的相关研究的目的。

1 中国部分微分几何学家谱系及其特征

1.1 中国部分微分几何学家的学术谱系

一般认为，微分几何学的中国先驱主要是姜立夫、孙光远和苏步青[1，10]。他们早期都是到国外学习微分几何学，学成回国后共同努力在中国耕耘微分几何学，由此逐渐形成了微分几何学的中国学术谱系(图1)。

姜立夫的学术引路人是美国哈佛大学库利奇(J. L. Coolidge，1873—1954)，博士毕业后曾留校做奥斯古德(W. E. Osgood，1864—1943)的助教。孙光远是另一位留学美国并致力于微分几何学的中国早期学者，师从芝加哥大学莱恩(E. P. Lane)。苏步青则东渡日本，跟随东北帝国大学窪田忠彦学习和研究仿射微分几何学，使得苏步青不仅是微分几何学的中国早期学者，而且也是日本培养的第一位国外微分几何学家。

除了美国和日本之外，德国、法国和英国等也对中国早期微分几何学产生非常重要的影响。对中国微分几何学产生影响的德国数学家主要有汉堡大学的布拉施克(W. J. E. Blaschke，1885—1962)和凯勒(E. Kähler，1906—2000)。布拉施克曾与日本的窪田忠彦师出同门[4]，他曾培养了他的第一位中国微分几何学家汤璪真，后来，李森林受汤璪真的影响也走上了微分几何学研究之路。布拉施克曾受邀到北京大学讲学，改变了吴大任和陈省身的学术研究方向。吴大任和陈省身都是在南开大学受到姜立夫的影响而走上微分几何学之路，后来两人同时考取了清华大学研究生，师从孙光远继续学习和研究微分几何学，毕业后，两人到德国汉堡大学留学都跟随布拉施克；另外，陈省身在汉堡大学参加过凯勒主持的讨论班，学术受益匪浅。对中国微分几何学产生影响的法国数学家主要有巴黎大学的嘉当(E. Cartan，1869—1951)、斯特拉斯堡大学的埃瑞斯曼(C. Ehresmann，1905—1979)。嘉当在巴黎大学曾先后培养了两位中国微分几何学家，他们分别是陈省身和李华宗。陈省身跟随布拉施克获得博士学位后，到法国巴黎大学做嘉当的助教；李华宗在英国师从爱丁堡大学斯图伊克(D. J. Struik，1894—2000)获得博士学位后，到法国也跟随嘉当继续研究微分几何学。其间，法国数学家埃瑞斯曼与陈省身曾同窗师从嘉当，此种关系对后来的中国留学生产生了较大的影响，主要有田方增、余家荣、严志达、吴文俊等曾先后到法国留学跟随埃瑞斯曼，学习和研究代数拓扑学或微分几何学。其中，严志达在西南联合大学跟随陈省身之后，由陈省身推荐，师从埃瑞斯曼继续研究微分几何学。

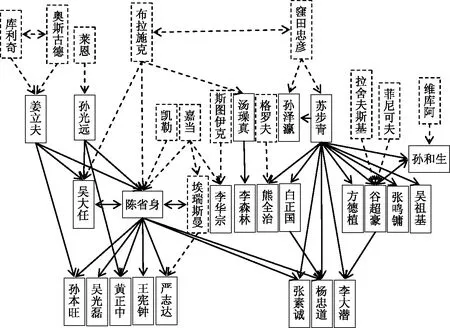
图1 中国部分微分几何学家学术谱系注：虚线表示国外导师，实线表示国内导师，单尖头被指的是学生，双尖头表示学术合作。

20世纪40年代，陈省身在整体微分几何学的研究方面有了突破性的进展，对整体微分几何学的发展产生了深刻的影响[11，12]。而这些成就主要得益于陈省身留学德国和法国的学术经历，其学术研究达到世界一流的水平。由此带动一批中国青年学子追随陈省身从事整体微分几何学或相关的研究，除了严志达外，还有孙本旺、吴光磊、王宪钟、黄正中等。孙本旺、吴光磊和王宪钟都曾在西南联合大学参加由陈省身组织的微分几何学讨论班，其中，孙本旺先期就曾师从姜立夫学习微分几何学，后来留学美国纽约大学柯朗(R. Courant，1888—1972)数学研究所，师从弗雷德里希(K. O. Friedrichs，1901—1983)，转向泛函分析和偏微分方程论的研究，并成功地将其应用于微分几何学；黄正中在上海交通大学毕业后，在南京大学工作中受到孙光远的影响，开始学习和研究微分几何学，后来曾得到陈省身的指导继续从事微分几何学研究。

日本数学家窪田忠彦曾先后培养了两位中国微分几何学家，他们分别是苏步青和孙泽瀛。其中，苏步青的中国微分几何学工作最为突出，不仅表现在学术研究方面，更重要的是培养了一批有影响的中国微分几何学家，形成了中国微分几何学派[9]，涌现了熊全治、张素诚、方德植、吴祖基、白正国、谷超豪、孙和生、张鸣镛、李大潜和杨忠道等杰出的数学家。其中，熊全治后来在苏步青的推荐下留学美国，跟随美国密西根州立大学格罗夫(V. G. Grove)继续研究射影微分几何学；杨忠道后来到中央研究院数学研究所跟随陈省身转向代数拓扑学，不久由陈省身推荐给美国图兰大学的华莱斯(A. D. Wallace，1905—1985)继续代数拓扑学；谷超豪后来到苏联进修，跟随拉舍夫斯基(П. К. Рашевский，1907—？)和菲尼可夫(С. П. Хиников)继续学习和研究微分几何学；张素诚后来到中央研究院数学研究所跟随陈省身转向拓扑学，不久到英国留学跟随怀特海(J. H. C. Whitehead，1904—1960)继续学习和研究拓扑学；孙和生后来到莫斯科大学跟随维库阿(И. Н. Векуа，1907—1977)学习和研究函数论，并将其应用于微分几何学，回国后，曾与谷超豪有过密切的学术合作；李大潜在复旦大学师从苏步青、谷超豪，后来到法国留学跟随里翁斯(J. L. Lions，1928—2001)转向微分方程论。

除了上述之外，还有华罗庚带领其学生陆启铿等曾涉足到与微分几何学有关的研究工作[3]，刘亦珩在西北大学组织黎曼几何专门化讨论班，带领一些学生开展微分几何学的研究[1]。

1.2 中国部分微分几何学家的学术谱系特征

1.2.1国内与国外导师并存

微分几何学是由国外移植到中国，并逐渐在中国得到发展，这决定了中国微分几何学家的学缘关系呈现出国内与国外导师并存的特征。早期，国外导师成为中国微分几何学家学术成长的主要学术引路人；后期，国内导师开始独立担当培养中国微分几何学家的重任，并成为主力军，但师从国外导师依然是中国微分几何学家学术成长的重要方式和途径。例如，姜立夫和孙光远早期师从国外导师，学成回国后参与中国现代数学建设，并以其微分几何学研究来带动对新一代中国微分几何学家的培养，陈省身就是典型的代表。陈省身在国内获得清华大学硕士学位后，到国外留学攻读博士学位，在布拉施克、嘉当等导师的影响下，学术研究很快进入学术前沿。而陈省身学成回国后，他继承先师的传统，在开展学术研究的同时，也担负起培养新一代中国微分几何学家的重任，培养了学生严志达等。后来，严志达留学法国师从嘉当的学生埃瑞斯曼。

1.2.2多个与单个导师共存

一般地，导师是数学家学术成长的关键，中国微分几何学家的学术导师表现为多个与单个共存的现象，有的只有一位导师，有的则受到多位导师的指导。导师的多少不仅仅是攻读学位的需要，更重要的是学术研究的需要。例如，窪田忠彦是苏步青在微分几何学的学术成长中唯一的导师，苏步青学成回国后就能够独立地开展研究工作，由此开创和领导了被国外同行誉为的“中国微分几何学派”，而他的有些学生在学术成长中考虑到学术研究的需要，曾受到多位导师指导，如谷超豪的学术导师有苏步青、苏联的拉舍夫斯基和菲尼可夫。

1.2.3链式与网状结构并存

中国微分几何学家学成回国后除了继续开展学术研究之外，还积极地参与中国现代数学的建制化建设，担负着人才培养的重任，其主要途径是在中国大学创建数学系、领导并组织微分几何学讨论班。这样，除了在国外留学师从同一位或相关联的导师之外，中国微分几何学家还由于国内各研究单位之间的学术交流而呈现出以师生关系为主、具有链式与网状结构并存的学术谱系。例如，姜立夫和孙光远开创的微分几何学群体和苏步青领导的微分几何学群体，是当时微分几何学在中国的两大重要学术群体，其成员在导师的推荐下相互交流。如张素诚、杨忠道在浙江大学跟随苏步青之后，师从陈省身学习和研究微分几何学或转向代数拓扑学。

2 微分几何学的中国学术传统与特征

学术谱系不仅反映了科学家的师承关系和合作者关系，而且反映了学术传统的传承、发展或转向；学术传统是维系一个包括学术谱系在内的学术共同体健康发展、不断取得成果的内在生命力[13]。

2.1 微分几何学的中国学术传统

微分几何学是一门既古老又年轻的学科，几乎与微积分同时产生和发展。到20世纪上半叶，微分几何学的基本发展态势是：1870年克莱因的《埃尔朗根纲领》发表后的半个世纪内，射影微分几何学的研究相当活跃，并且在传统的射影微分几何学的基础上，仿射微分几何学于20世纪20年代创立起来，其中苏步青领导的中国学术群体在仿射微分几何学领域做出杰出贡献，成为微分几何学的世界三大学派之一。另一个重要发展方向是嘉当把李群和微分几何结合起来，成功地建立了外微分流形理论和活动标架法，奠定了现代微分几何学的基础，由此，到20世纪40年代，形成了整体微分几何学，其中陈省身在高维黎曼流形上的推广方面做出了重要贡献，成为整体微分几何学的重要贡献者之一。等距浸入和子流形几何也是当时微分几何学的一个重要研究方向，但中国很少涉及[14]。正是在当时这样的微分几何学蓬勃发展的大背景下，微分几何学开始引入中国，并很快开展了卓有成效的工作。同时，由于受到中国时局、学术研究、学术条件等多种因素的影响，微分几何学在中国主要形成了两个代表性的学术传统：一个是姜立夫和孙光远开创的射影微分几何学的中国学术传统，后来由陈省身发展到整体微分几何学传统；另一个是苏步青领导的仿射微分几何学传统。

2.1.1由射影微分几何学传统到整体微分几何学传统

姜立夫在美国哈佛大学库利奇的指导下，运用代数和微分几何方法来研究射影空间的直线和非欧空间的球面之间的关系。孙光远是受美国导师莱恩的影响，从事射影微分几何学的研究。姜立夫和孙光远先后学成回国后，都是将布拉施克编著的《微分几何学讲义》(VorlesungenUberDifefretialGeometrie)作为教材在中国传播微分几何学，后来，将布拉施克邀到北京大学讲学，使其学术传统在中国得到很好的传承。吴大任继承了姜立夫、布拉施克的学术传统，从事积分几何、射影几何、非欧几何、微分几何等研究，将积分几何的运动主要公式推广到三维及以上空间，证明了关于欧氏平面和空间中的凸体弦幂分的一系列不等式等。陈省身在布拉施克的指导下，运用嘉当方法即活动标架法和等价方法来研究微分几何，后来陈省身跟随嘉当，直接继承了嘉当的学术“衣钵”——微分形式的运算，并受代数拓扑学的启示而创建了外微分方法。这种方法不仅揭示了外微分与积分是两个互补的运算，而且揭示两者都与斯托克斯定理相联系，这是目前用于解决由嘉当所开创的将几何结构的等价转换成微分形式组的等价问题的最为理想的方法。此外，此时的纤维丛及主丛上的联络理论在嘉当的带领下也刚刚发展起来，外微分方法也是将等价问题与联络理论联系起来，陈省身发现了一种内蕴联络，并给出了高斯-邦内特公式的内蕴证明。随后，陈省身受到埃瑞斯曼工作的启示，发现复流形上的不变量-陈示性类，由此，使陈省身成为示性类理论的原创者之一。1946年，陈省身发表的《大范围微分几何的某些新观点》，指出了嘉当的联络思想与纤维丛理论的密切关系，从而把微分几何进一步推进到大范围微分几何。总之，陈省身受到布拉施克、嘉当和埃瑞斯曼等的学术影响，在整体微分几何学的研究有了突破性的进展，使陈省身成为整体微分几何学的重要开拓者之一[15—17]，也就是说布拉施克、嘉当和埃瑞斯曼的学术传统在中国成功地得到发展。

此外，李华宗继承他的导师斯图伊克对张量微分几何的研究，后来也受嘉当的影响，开展了微分几何学中关于施考特恩(J. A. Schouten)的接触变换研究。汤璪真博士毕业后回国直接使用其师布拉施克的德文著作《微分几何讲义》在国内大学进行教学，同时也开展相关的微分几何学研究。李森林在武汉大学受到汤璪真的影响而对微分几何学产生兴趣，后来受到国内数学专业发展的影响，转向微分方程论研究。

陈省身学成回国后继承先师的传统，并担负起培养新一代数学家的重任，其中有一部分学生从事整体微分几何学或相关的研究，使其学术传统在中国得以传承和发展，代表人物有严志达、孙本旺、吴光磊、王宪钟和黄正中等。严志达、孙本旺、吴光磊和王宪钟主要是在西南联合大学参加由陈省身主持的微分几何讨论班，系统地学习了布拉施克和嘉当的几何理论，其中包括重要的李群理论，这对于他们后来从事微分几何学的研究产生了重要的影响。其中，严志达后来到法国留学师从埃瑞斯曼，在李群的拓扑方面和曲面丛的几何方面有新的突破，如在嘉当理论的意义下考察K维元素射影联络空间；孙本旺后来前往美国留学，师从弗雷德里希转入研究泛函分析和偏微分方程，并将其成功地应用到与微分几何学有关的四维辛空间的曲线和超曲面研究；吴光磊的主要工作是算出了丛的贝蒂数(Bitti number)，证明了在子流形的法丛上的高斯-邦内特公式；王宪钟早期从事活动坐标架理论和射影微分几何的研究，西南联合大学毕业后参加由陈省身在中央研究院数学研究所主持的拓扑学讨论班，开始转向拓扑学，后来，留学英国曼彻斯特大学师从纽曼(M. H. A. Newman，1897—1984)继续拓扑学研究。黄正中在上海交通大学任教时曾受到陈省身的指引而走向微分几何学研究，也取得了一些重要成果，例如，对于C1黎曼流形给出鉴定法坐标的充分必要条件，首次解决了托马斯(T.Y.Thomas，1899—？)所提出的n-1型和n-2型黎曼空间，对空间曲线的封闭性提出鉴定方法等等。

2.1.2苏步青领导的微分几何学学术传统

苏步青是在继承窪田忠彦学术思想的基础上发展了微分几何学，其中包括著名的“苏步青锥面”“苏步青链”，这成为整个仿射微分几何曲面论的核心，苏步青成为仿射微分几何学的领导者之一，由此也奠定了他领导的微分几何学学术传统的基础。

苏步青曾先后在浙江大学和复旦大学开展教学与研究，组织和领导微分几何学讨论班，由此取得了卓有成效的工作，该群体被誉为“中国微分几何学派”，主要成员包括熊全治、方德植、谷超豪、张素诚、吴祖基、白正国、孙和生、张鸣镛和李大潜等。其中，熊全治早期开展局部射影微分几何研究，后来在美国留学师从格罗夫，转向整体微分几何，特别是积分几何；方德植的研究工作受苏步青的影响非常大，研究了仿射曼赫依姆曲线(Mannheim curve)等，将苏步青所研究的射影微分几何的曲面进一步推广到射影微分几何的曲线；谷超豪成功地解决了苏步青所提出的K展空间理论中一个未能解决的问题，后来到莫斯科大学访学，受拉舍夫斯基和菲尼可夫的影响，研究无限连续变换拟群等；张素诚早期在苏步青的基础上开展有关平面曲线奇异点的研究，后来受陈省身和怀特海的影响，转向拓扑学；吴祖基创立了“吴氏二曲面”，开创了与曲面共变的渐近直纹面的研究；白正国开展射影曲面论的研究，解决了射影微分几何学中著名的富比尼问题(Fubini’s problem)，后来转向一般空间的微分几何学的研究，特别是在闭曲线的整体几何学的研究，推广了著名的芬切尔定理(Fenchel’s theorem)；孙和生在苏步青的指导下，结合吴新谋和维库阿的学术思想，将广义解析函数论应用到微分几何曲面变形论；张鸣镛早期主要是对芬斯勒流形(Finsler manifold)做出了一些重要成果，后来到厦门大学转向函数论的研究；李大潜早期在苏步青领导的学术团队的熏陶和训练下，曾在闭曲线的整体几何学领域有所成就，但是后来留学法国师从应用数学家里翁斯，转向应用数学研究，再后来与谷超豪在微分方程论领域开展合作研究。

由上可见，微分几何学的中国学术传统已基本形成，这是在继承国外优秀学术传统的基础上由数代中国微分几何学家共同努力的结果，同时，也可以看出导师起到的关键性影响。但令人惋惜的是，由于国内战争等多种因素的影响，陈省身后来到美国工作，对中国的整体微分几何学发展影响比较大：虽然陈省身继承前辈并开辟微分几何学的中国新传统，且继续发挥其积极的作用，但是正处在学术发展关键时期的陈省身离开中国前往美国，从某种程度上来说，削弱了整体微分几何学在中国发展正劲的势头，而对美国几何学的快速发展发挥着举足轻重的作用，“复兴了美国的微分几何，形成了美国的微分几何学派”，“就美国几何学复兴的一个决定性因素而言，我认为是陈省身于20世纪40年代末由中国移居到美国发挥着决定性的作用”，并且培养了野水克己(Katsumi Nomizu)、奥斯兰德(L. Auslander)、丘成桐等杰出的微分几何学家[15]，从而使美国在微分几何学领域走到世界的前沿。

2.2 微分几何学的中国学术传统的特征

2.2.1源起并发展于国外优秀的学术传统

微分几何学的中国学术传统源起于国外。20世纪初微分几何学处于迅速发展时期，中国学子跟随国外导师才开始接触和学习微分几何学，这也显示了中国微分几何学学术传统所具有的显著特征：他们的导师基本上都是当时微分几何学的权威或领导者。因此，他们不仅跟上了微分几何学的发展主流，而且继承了国外导师的学术思想和学术风格，奠定了微分几何学的中国学术传统的良好基础。例如，苏步青师从窪田忠彦开始了他的微分几何学学术之路，而窪田忠彦曾与布拉施克同窗，是当时射影微分几何学发展的主要领导者，其中布拉施克是当时仿射微分几何学的主要开创者，窪田忠彦的学术传统为苏步青后来在仿射微分几何学的研究奠定坚实的基础，开创了所谓的“苏步青锥面”“苏步青链”，使苏步青成为仿射微分几何学的主要贡献者和领导者。又如，陈省身在布拉施克和嘉当的指导下，迅速达到微分几何学研究的前沿，证明高维的高斯-邦内特公式，提出了陈示性类，为整体微分几何学的建立奠定了基础[18]。

2.2.2融入微分几何学的发展主流

微分几何学引入中国后，中国微分几何学家便开始独立开展研究，并在国内组织一些微分几何学讨论班，将在国外学习或正在研究的微分几何学作为讨论和研究课题，从而紧跟微分几何学前沿问题研究的步伐。同时，采用“请进来，走出去”的办法，先在国内打基础，后到国外继续深造。从而使中国能够基本上融入微分几何学的发展主流，并有机会达到学术前沿。例如，严志达、孙本旺、吴光磊和王宪钟都是在西南联合大学参加由陈省身主持的微分几何讨论班，学习和研究“黎曼几何”“圆球几何学”和“外微分方程”等课程，这些课程都是陈省身在德国和法国留学时学习的最新内容，甚至是其正在研究的整体微分几何学的相关课题。他们有了对学术前沿的认识，后来相继到国外深造，继续围绕整体微分几何学而开展相关的研究。

2.2.3学术研究同国家命运与发展相结合

现代数学引入中国之际，中国青年学子正经受着20世纪初“辛亥革命”“五四运动”等的影响和洗礼，“科学救国”思想深入到中国青年学子的心中。在这样的社会大背景下，中国微分几何学家从一开始便怀揣“科学救国”思想，将国家命运与发展同其学术研究紧紧联系在一起，并且把这种学术追求和精神信念深深地融入在他们的学术研究中，通过言传身教潜移默化地影响着后来者，成为一种学术的精神传统代代相传，这是微分几何学的中国学术传统最显著、独特的特征。例如，姜立夫在时代背景的感召下，通过考试赴美国留学，并且立下了“中国要富强起来，需要科学，数学是科学的基础，因而需要数学，立志要把现代数学移植于中国”的宏愿。在1919年5月，姜立夫获得博士学位后，在哈佛大学工作期间，欣然接受南开大学聘约回国，于1920年初在南开大学创办数学系。由此，姜立夫成为现代数学在中国最早且最富成效的一位播种人，并为中国现代数学事业贡献了毕生精力。姜立夫的学术传统和爱国精神在中国得到继承和发展，陈省身就是典型代表之一。陈省身在国内接受高等数学教育之后，留学德国和法国，此时的他在学术上开始崭露头角，但是他放弃国外优厚的待遇和优越的学术环境，毅然回到仍处在艰难抗战中的中国，并在非常艰苦的条件下在西南联合大学开展了富有成效的科研与教学工作，除了多篇论文发表在《数学纪事》(AnnalsofMathematics)等一流数学期刊上之外，更重要的是培养了很多优秀的青年数学家，如严志达、王宪钟、吴光磊等，他们后来都成为中国现代数学的中坚力量。

3 启示

微分几何学之所以在中国取得成就，主要是由于中国历代微分几何学家在模仿、摸索中推动微分几何学在中国的发展。因此，其背后也蕴涵着微分几何学在中国发展的某些规律，这为建设数学强国带来一些重要的启示。

3.1 关于中国微分几何学家的学术成长

(1)建立符合中国国情的人才培养机制。姜立夫等先驱者在模仿国外传统的基础上，努力在中国探索建立以学术研究带动人才培养的机制，也就是将学术研究同人才培养结合起来，引导学生通过解决微分几何学中的若干问题来逐渐促成他们的学术成长、塑造他们的学术精神。这种机制在后来得到很好的继承、巩固和发展。因此，促成中国数学家学术成长机制时，应进一步加强、完善或开拓以学术研究推动人才培养的中国学术机制。

(2)发挥导师的学术主导作用。中国微分几何学家在学术成长过程中，授业导师呈现多样性，不仅有国外导师，而且有国内导师，并且导师数量多寡不等。这些现象的背后起主导性作用的是导师的学术影响，导师的学术研究以及由此形成的学术传统影响和决定了跟随者的学术研究方向，从而也进一步地引导他们挑战微分几何学中的一些重要问题，在微分几何学发展主流中开展中国的原创性工作。因此，在制定促成中国数学家学术成长机制时，应注意建立导师全面负责制度，由导师的学术研究或由导师推荐来引导和影响学生逐步走上学术前沿[19]。

3.2 关于中国微分几何学的发展规律

(1)学术研究同国家命运与发展的结合。最早一批的中国微分几何学家都深深受到“五四”爱国运动的影响，“科学救国”促其努力开展学术研究，并且代代相传，“科学救国”的学术精神成为支撑其开展学术研究的主要精神动力。因此，中国现代数学发展应继承和发展这种将科研同国家发展相结合的精神动力，使之成为中国数学家刻苦工作的精神支柱和奋斗的力量源泉。

(2)在紧跟主流中展现创新。中国微分几何学家们开展学术研究主要是采取跟随方式，表现为从引入的开始便始终紧跟微分几何学发展主流。在这种跟随中,中国微分几何学得到长足的发展，在某些领域开始跻身于学术前沿，已有一些原创性的中国成果。因此，中国现代数学发展要融入到世界数学发展主流中，在紧跟主流的发展过程中，试图在若干条件成熟的领域争取有较大的突破，由此来做大做强中国现代数学。

3.3 关于中国微分几何学家的学术自信

中国早期微分几何学家在其学术刚刚起步的阶段之所以敢于选择、挑战学术前沿甚至当时是冷门的问题，其中无疑蕴涵着他们对其学术研究的自信，而这种信念主要源于他们所继承和发展的国内外优秀的微分几何学传统，形成于其学术研究和深度交流中。例如，陈省身由继承国内射影微分几何学转向整体微分几何学时，整体微分几何学当时还是冷门方向，陈省身在当时开展研究的过程中同样也受到过一些冷遇等现象，但他并没有由此而退缩、抱怨。相反地，陈省身有更加坚定的信心，这是因为：一方面，他与当时已是著名数学家的外尔(H. Weyl，1885—1955)、韦伊(A. Weil，1906—1998)、韦布伦(O. Veblen，1880—1960)等对于整体微分几何学形成了一些学术共识[2]；另一方面，他在整体微分几何学研究的过程中已形成并具备了对学科发展的敏锐性。因此，现任中国数学会理事长田刚教授在其就职报告中特别提到当前中国数学家的学术自信问题等。我们可以从中获得一点借鉴：中国现代数学家应该继承国内外优秀的学术传统，在学术研究和深度交流的过程中探索学术发展的共识，提高关于学术原创的敏锐度，克服学术“无人区”的心理障碍，从而确立学术自信。