《〈数度衍〉评林》初探

徐 君

(包头师范学院数学科学学院，包头 014030)

1 引言

《数度衍》(1661)是清初数学家方中通(1634—1698)的著作。全书共26卷，卷首分为数源、律衍、几何3卷，其余23卷，分述珠算、笔算、尺算、筹算等知识[1]，涉猎内容非常广泛，因此《数度衍》被史学家称为“是当时一部数学上的百科全书”[2]。江户(1603—1867)时代，中国传统数学东传日本的规模很大，前所未有。此间《数度衍》于1726年传入日本[3]，户板保佑(Toita Yasusuke，1708—1784)《关算完传》101卷(1780)转载了《数度衍》[4]，《数度衍》在关流中流传开来。小出兼政(Koide Kensei，1797—1865)所著的《〈数度衍〉评林》(天保4年，1833)是针对《数度衍》首卷“数源”与卷八“测圆”进行评论，也是现今极少可见的《数度衍》传到日本后对其进行讨论的史料证据。小出兼政，通称长十郎，字修喜。文政2年(1819)获宫城流皆传，文政9年(1826)6月入和田宁(Wata Yasushi，1787—1840)之门，同年8月师从日下诚(Kusaka Makoto，1764—1839)，受关流宗统皆传，另受最上流传百余卷。文政12年(1829)随关流大家和田宁受圆理豁术，故而自称为“四流兼学”(宫城流、关流、最上流、和田宁流)[5]。

现代中算史家对《数度衍》的研究多是从版本、内容以及取材来源等角度评述[2，6，7]，而东传日本的情形尚未涉及。《数度衍》传入日本一百多年后，已是和算发展晚期，小出著《〈数度衍〉评林》对《数度衍》内容进行探讨，自然引发研究者的关注。例如，小出著《〈数度衍〉评林》目的是什么，为什么仅选择“数源”与“测圆”两节内容进行评论，小出又做了怎样的工作，有何创新之处等问题。基于此，本文尝试对《〈数度衍〉评林》进行考查，展现小出对东方传统数学文化的理解与看法。

2 《〈数度衍〉评林》之内容

《〈数度衍〉评林》(图1)主要分为两部分：第1部分是对《数度衍》首卷“数源”节中方阵(纵横图)的分析讨论，又介绍了聚环与圆攒等内容；第2部分是结合点窜术对《数度衍》卷八“测圆”节勾股内容圆问题的推理演算。

图1 《〈数度衍〉评林》书影

2.1 方阵

《数度衍》首卷“数源”节中载有三阶、四阶至十阶的纵横图，但只有图而没有具体的构造方法。因而小出认为《数度衍》一书中虽给出三到十方阵的结果，但并没有明确指出方法，即“为能尽人心之劳”[8](1)以下引文皆出此处，不再注明。。小出把方阵分为奇、偶两种情况。第一奇方阵：

评曰：以洛书称方阵，天理自然奇数也，三方、五方、七方皆谓奇方阵。随天数始于坎宫终于离宫，以中数(三方者五，五方者十三，皆仿之)为中央，以其方阵数(三方者三，五方者五)充震宫，是则洛书之本意也。

从位置角度给出一种构造奇方阵的思想。为说明需要，小出进一步定义了相关术语，以三阶方阵为例：

图2 洛书图

经纬之数各十五个，斜之数又相同(东西谓经，南北谓纬，以下仿之)。

如图2所示，其中采用八卦为主要术语，二、四、六、八、一、三、七、九分别处在方阵图中的坤、巽、乾、艮、坎、震、兑、离位置，即用八卦表示奇方阵中的八个方位。同时规定横为“经”，竖为“纬”。

可将“原表”作成如下形式的位置表(表1)：

表1 原表与译图表对照表

其中aji(i，j=1，2，…，n)，代表i经j纬的数字。则可知表中a32代表数字八，a23代表数字六，如此类推。小出以三、五阶方阵为例，解释从原表推算出侧书的过程，并找到规律，列表如下(表2)：

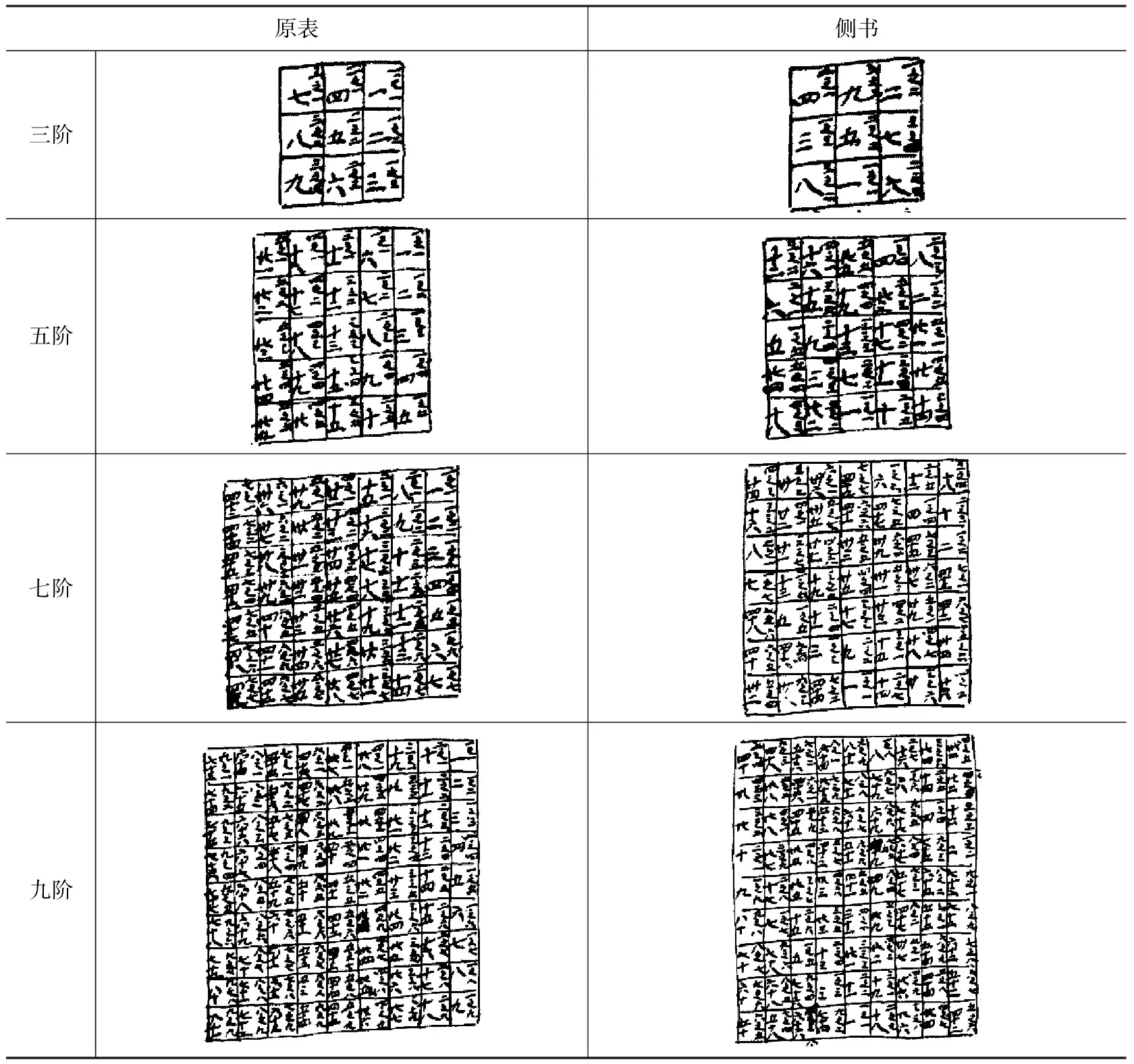
表2 原表推算侧书的过程

从而总结出求解奇方阵的一般方法，具体如下，先列出“原表”图(图3)，其中n=3，5，7，…。

之后求解侧书图，按以下规律填写数字：

图3 奇方阵通用原表图

图4 奇方阵通用侧书图

(2)填充震宫位置的数为a1n，即“以其方阵数充震宫”，以“中纬行”为对称轴，得到兑宫位置的数为an1，同时下标数j按从1至n的顺序填写，而i的顺序与j相反，可找到“中经行”。

(3)“中纬者”的下标数j是从1至n，由北向南顺次排列，即“顺升”。处在中纬行东侧位置的下标数依次“进位”(例如1，2，3，4，5。进一位为5，1，2，3，4；进二位为4，5，1，2，3；其他仿此)之后“顺升”，即“东纬者进位顺升”。而处在中纬行西侧位置的下标数依次“退位”(例如1，2，3，4，5。退一位为2，3，4，5，1；退二位为3，4，5，1，2；其他仿此)之后“顺升”，即“西纬者退位顺升”。

(4)“中经者”的下标数i是从1至n，由西向东顺次排列，即 “一二三顺行”。处在中经行南侧位置的下标数“自二始”，之后依次“顺旋”，即“南经者自二始顺旋”，而处在中经行北侧位置的下标数始自n，之后依次“顺旋”，即“北经者自三(n)始顺旋”。

这样，小出又以五方阵为例验证此法的正确性，并进一步推导出七方阵与九方阵图，而小出所得结论与《数度衍》原书中的不一样，显然是由两人所用方法不同所致。

第二“偶方阵之解”。原文有：

夫偶方阵者有二种，一者以四方、八方、十六方为质题；一者以六方、十方、十二方为文题。是谓奇偶因数，六则二与三相乘(二、三之六)，十则二与五相乘(二、五之十)，十二则三与四相乘(三、四之十二)也。奇偶相因之数则别有补术焉。偶者坤二、巽四、乾六、艮八也，皆在隅宫。视于偶方阵之中央无中间可座之所,坎宫、离宫亦同，奇偶之术所以异矣。

小出的“质题”原图列表如下(表3)：

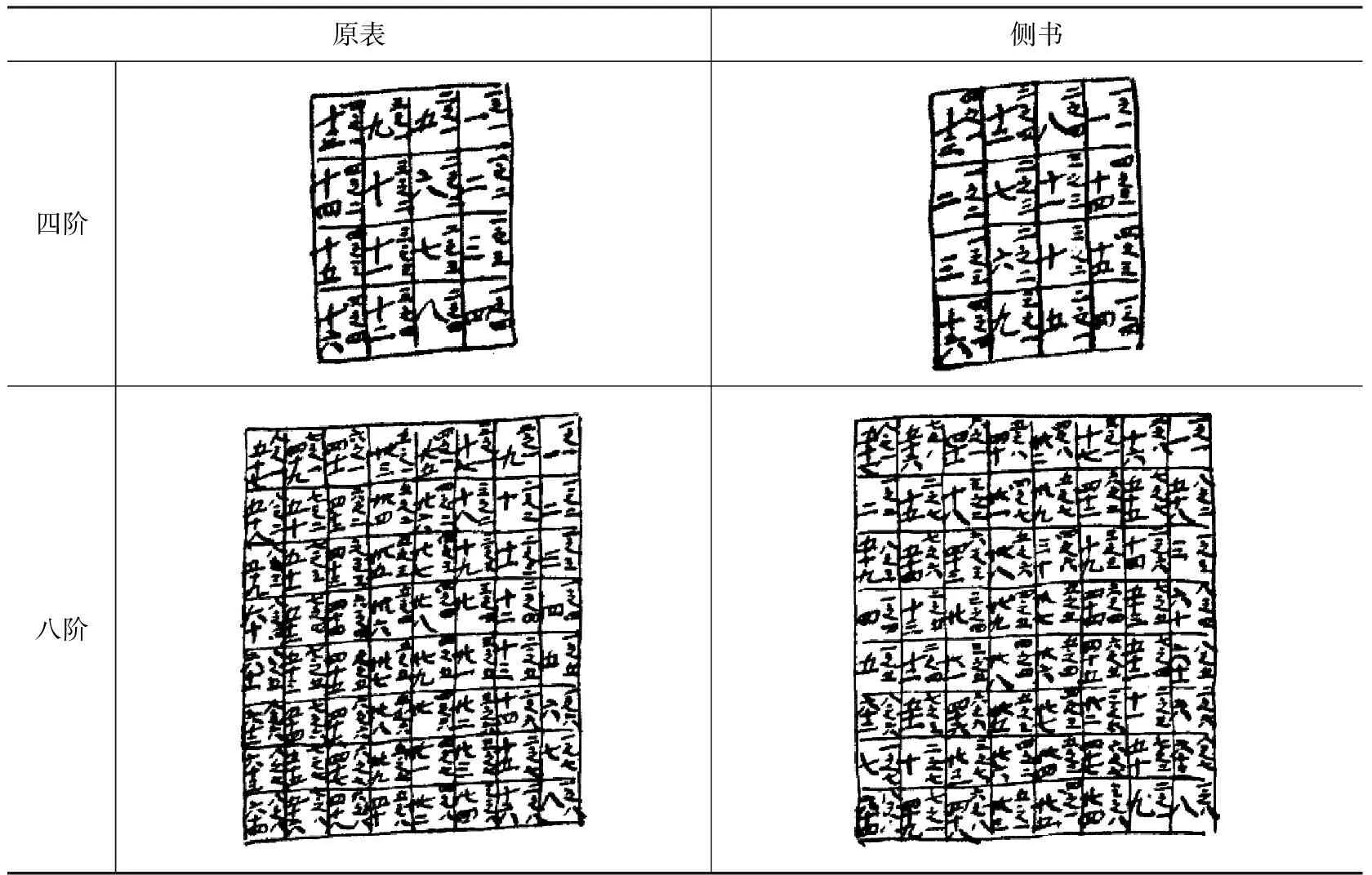
表3 小出的“质题”原图与侧书

图5 质题方阵通用侧书图

2.2 勾股内容圆问题

小出在“勾股内容圆之条”中说：“夫以勾股者，矩之根元，而算家不依于此理而何得方理之术乎。方成而后求圆理，皆在此勾、股、弦之三件。今本书(《数度衍》)勾股内容圆术凡八十八题(2)实际上是89道题，原文数量计算有误。，各难问也，视其术则最能竭，借字显术不备解矣。”

指出“勾股”之“理”在和算中的重要意义，且称赞《数度衍》中“勾股内容圆术”的89个问题“视其术则最能竭”，但其中的不足是“借字显术不备解”。因此小出结合点窜术逐一地对89问进行推算证明，以下仅选择第1题进行介绍，以现其旨(表4)。

表4 《数度衍》“勾股内容圆术”第1题图文对照表

《数度衍》原文的解法：“勾股相乘，得十二万二千八百八十。倍之，得二十四万五千七百六十为实。勾股求弦，得五百四十四，以并股，得一千○二十四为法。除实得二百四十为圆径。”

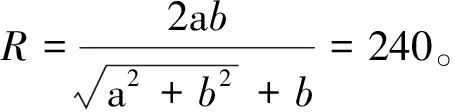
表5 推算过程原文与译文对照表

续表5

3 讨论

由上可知，小出给出一种构造方阵的新方法。在勾股内容圆问题中，逐一详细地为每个问题列出求解过程，补充《数度衍》中没有做的工作，并表现出了一定的解题技巧。当然，小出在此所做工作并不仅是为了补充方法这么简单，还有更深的寓意。为此，先对中日“纵横图”的发展历程进行简要回顾。“纵横图”一词，由南宋杨辉首创，易纵横图起源于易数研究，数学之中纵横图可能受到易纵横图的启发，甚至可能直接源于易数研究[9]。汉代已有了三阶纵横图，称为九宫图。到了13世纪纵横图开始向高阶发展，杨辉《续古摘奇算法》(1275)中已有了十阶纵横图，此外还有幻圆等组合图形。与他同时代的丁易东在其《大衍索隐》中也对纵横图颇有研究[10]。在明朝王文素的《古今算学宝鉴》(1524)和程大位的《算法统宗》(1592)中有不少关于纵横图的讨论。《算法统宗》给出纵横图14种，这些图大部分与杨氏的图相同，仅有“五五图”“六六图”“聚六图”“八阵图”4种稍异。方中通《数度衍》载纵横图14种，大部分引自程氏《算法统宗》，仅“五五图”与程氏的图稍有不同。随着中算数学著作传入日本，和算家对方阵也进行了研究,给出多种方法。如有：关孝和(Seki Takakazu，1642？—1708)的《方阵之法·圆攒之法》(1683)明确总纲，以例说明构造。建部贤弘(Takebe Katahiro，1664—1739)的《建部先生方阵新术》(年代不详)用格交换方法构造方阵。久留岛义太(Kurushima Yoshihiro，？—1757)的《方阵之法并解》(年代不详)采取斜进法说明构造过程。还有松永良弼(Matsunaga Yoshisuke，？—1744)、安岛直圆(Ajima Naonobu，1732—1798)等人都曾研究过纵横图的构造方法。但小出的方法与以上各法都不同，小出的方法应源于宅间流五代传人松岡能一(Matsuoka Yoshiichi，1737—1804)的《方阵圆阵解》(年代不详)，通过内容比较可发现，在求奇方阵时，小出的构造法与松岡一致，但松岡没有给出任何文字解释，使读者较难理解其中的道理，小出则给出了细致、全面的说明。求偶方阵时，小出给出了构造“质题”方阵的新方法，松岡则没有发现这一做法。

再看勾股内容圆问题的发展过程。勾股容圆问题可追溯到方中容圆、圆中容方等相容问题，中国现存最早的数学著作《算数书》中就有“以圆材方”和“以方材圆”的问题[11]。《九章算术》初次载有勾股容圆问题，即已知勾股形的勾、股，求其内切圆的直径。到宋、元时代，勾股容圆成为重要的研究专题，集中体现于李冶(1192—1279)的《测圆海镜》(1248)。书中以“圆城图式”为核心，构造性地编创了170道题[12]。《数度衍》中的勾股内容圆问题根源于李冶的《测圆海镜》，但从方氏收录的内容来看，应是受到了顾应祥《测圆算术》(1553)的影响。早期的和算著作中也有许多关于勾股容圆问题的记述，如村松茂清(Muramatsu Shigekiyo，1608—1695)的《算俎》(1663)，泽口一之(Sawaguchi Kazuyuki，生卒年不详)的《古今算法记》(1671)，井关知辰(Izeki Tomotoki，生卒年不详)的《算法发挥》(1690)等，其特色是把勾股容圆题改变为勾股内容两圆、三圆等问题。之后，勾股容圆问题研究朝着容多圆的方向发展，有马赖徸(Arima Yoshihiro，？—1757)的《拾玑算法》(1769)、藤田贞资(Fujita Sadasuke，1734—1807)的《精要算法》(1781)，以及安岛直圆的《不朽算法》(1799)等书，又创造了许多与勾股容圆相关的奇特图形问题。

另外，还有必要指明小出所使用的符号体系点窜术。点窜术可追溯到关氏的傍书法，傍书法源于天元术。关氏傍书法不仅可表示分数与无理数，还改天元术的筹算为笔算。特别是多元高次方程符号表示法的建立，既可以在解题中对方程进行恒等变形，又可以消去某些没有必要的未知量，这种计算方法称作演段术。傍书法与演段术合起来称为点窜术。点窜术后经建部贤弘、松永良弼等和算家的发展与改进，构成了和算的符号体系。

小出所采用点窜术的基本符号书写方法如下所示(表6)：

表6 小出所采用点窜术的基本符号书写方法与今译符号对照表

中间的竖线来源于中国古代的算筹，当为负数时，在竖线上加一斜线。竖线还等同于现代的分数线，在竖线的左右两侧书写文字，右侧为分子，左侧为分母。由于中间的竖线源于算筹，所以在计算过程中，系数有时也用筹式表示，即中国古代的算筹表示法。通过前面的介绍可知，在具体的解题过程中，点窜术不仅能准确展现出计算过程，还能很好地表达数学家的思维过程，同时体现数学符号语言的简洁与高效。

可见，和算家对中算纵横图、勾股容圆问题和数学符号的继承与发展，即中算与和算一脉相承，中算是和算的母体，和算的问题、语言、方法来源于中算或由中算衍生、发展而来，且上述数学知识在和算中也得到较好发展并成体系。小出也深明此理，他指出：“夫以勾股者，矩之根元，而算家不依于此理而何得方理之术乎。方成而后求圆理，皆在此勾、股、弦之三件。”即“勾股”源于中算，“勾股”是“矩之根元”，有了此理才推出“方理之术”，进而有了和算中优秀成果“圆理”。从而可揭示出小出著《〈数度衍〉评林》的目的，就是数学的传承与发展要有新问题的提出、新方法的出现以及数学符号语言的改进，即创造性的继承是数学文化发展与延续的保障。小出之所以借助《数度衍》一书来阐述自己的观点，主要应有四个原因：第一，方中通著的《数度衍》主张的是“西学中源”说，其中包含有中算为主的东方传统数学文化源远流长之意。第二，方中通在介绍纵横图与勾股内容圆问题时都没有给出计算方法，也为小出研究工作提供了空间。第三，小出所讨论的纵横图与勾股算术内容在中算与和算中一直都有着较好的发展，不仅传承时间久远，而且各种构造方法也层出不穷，借此能较好地说明东方传统数学文化源远流长的原因。第四，《数度衍》一书的内容几乎收录了当时中国传统数学中的全部内容，选择对《数度衍》进行评论，更能突显宣扬东方传统数学文化的意义。

4 结语

以汉字文化圈整体视域研究东亚数学史，不仅历史资料互补，而且通过对和算、东算的汉文化溯源以及对中算在周边国家发展态势的考察，可以深化对各国数学史的理解与认知，进而认识东亚数学的共同特征[13]。《〈数度衍〉评林》不仅体现了小出对数学文化传承与发展的认识，也反映了中算与和算之间的关系。和算家对方阵构造法的探究、勾股容多圆问题的发展和点窜术符号体系的建立，说明和算在中算的基础上，创造了新的数学问题、语言、方法，这正是和算文化体系逐渐形成的原因之一。小出重视数学思想方法在数学中不可或缺的地位，应推陈出新，而方中通在“西学中源”思想指导下编写《数度衍》一书，强调中算文化历史的源远流长。不管东方传统数学文化或“兴”或“衰”，数学家都会孜孜以求，研究不殆，究其根因，是数学家对东方传统数学文化的自信、自强、自立。可以说，创造性的继承是数学文化发展与延续的保障，文化自信是数学文化生存的根基。