电化学阻抗谱物理模型求解方法

李琛坤，王 帅，黄 俊

（1中南大学化学化工学院，湖南 长沙 410083；2乌尔姆大学理论化学研究所，德国 乌尔姆 89069）

电化学阻抗谱(electrochemical impedance spectroscopy，EIS)具有原位、无损的优点，被广泛应用于电化学储能(二次电池、燃料电池)和转化器件(电解池等)的性能监测、故障诊断和参数辨识[1-3]。在EIS实验中，我们用电化学工作站先将测试体系控制在一个稳定状态，然后施加微弱的电压或电流激励，测试相应的电流或电压响应。傅里叶变换后的电压和电流的比值即定义为阻抗。

其中，F表示傅里叶变换算子。测量不同频率下的阻抗便构成了EIS。

对测量得到的EIS 进行解析，需要相应的模型。常见的模型分为等效电路模型[4-5]和物理模型[1,6-7]。等效电路模型是指用电路元件(电阻、电容和电感等)的串并联来模拟研究体系。如图1 所示，物理模型是指将研究体系内发生的物理过程用相应的控制方程来描述。求解控制方程，即得到EIS的解析解或数值解。李响等人[7]详细推导了多孔电极EIS 的表达式，并细致分析了不同过程对EIS 响应的影响。等效电路模型的优点在于通用性好、计算量小和操作简单，缺点是物理机理不明确。程蕾等[8]推导了玻碳电极界面EIS的等效电路模型。通过拟合实验数据，定量对比分析了修饰前后电极表面的特征变化。由等效电路模型衍生而来的弛豫时间分布(distribution of relaxation times，DRT)[9]可以有效辨识不同过程的时间常数和阻抗，一定程度上辨析内部机理，因此得到了广泛的应用。物理模型的优点在于对体系内的物理过程描述清晰，适用于研究内部机理。基于控制方程建立的物理模型则有助于解析实验数据，辨析机理。因此，本文主要围绕物理模型展开介绍。

图1 (a)EIS测试原理；(b)典型的EIS实验结果；(c)物理模型构建原理(其中i0为交换电流密度，c为浓度，D为扩散系数)；(d)2阶RC等效电路模型Fig.1 (a)Principle of EIS measurement;(b)Typical experimental results of EIS;(c)Principle of physical model construction,(i0 is the exchange current density,c the concentration,D the diffusion coefficient);(d)Equivalent circuit model of second-order RC

本文首先介绍了EIS物理模型三种常见的求解方法：解析求解，时域数值方法和频域数值方法。其中，解析求解指通过合理假设，推导出EIS的解析表达式。时域数值方法指利用有限元等方法在时间-空间维度求解微分方程，而后通过傅里叶变化得到EIS 的数值解。频域数值方法指在频率-空间维度求解微分方程，而后计算EIS数值解。介绍完三种方法后，本文以电池中常见的金属离子沉积反应为例，对比了不同方法的优缺点，并对每种方法的适用场景进行了分析。

1 三种计算方法介绍

下文将以一个经典的带有法拉第反应的双电层界面为例，具体介绍上述三种方法。笔者[10]此前对双电层的平衡、非平衡、交流状态下的建模进行了详细的推导和总结，可以作为初学者的指南，感兴趣的读者可以进行查阅。笔者[11]同时梳理了EIS 在电催化界面和反应中的研究和最新的进展。相比之下，本文重点关注EIS物理模型的求解方法。

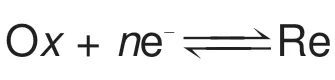
图2 (a)带氧化还原反应的电极/电解质溶液界面示意图；(b)EIS解析解的Nyquist图；(c)基于时域数值方法的EIS数值解与解析解的对比；(d)基于频域数值方法的EIS数值解与解析解的对比。频率范围为105～10-4 Hz。其余参数如下：c0 = 0.1 mol/L，D = 1 × 10-10 m2/s，j0 = 1 A/m2，α = 0.5Fig.2 (a)Schematic diagram of electrode/electrolyte solution interface with a redox reaction;(b)Nyquist plot of analytical solution of EIS;(c)Comparison of numerical and analytical solutions of EIS based on TSM numerical method;(d)Comparison of numerical and analytical solutions of EIS based on FSM numerical method;Frequency range is 105～10-4 Hz.Other parameters are as follows:c0=0.1 mol/L,D=1×10-10 m2/s,j0=1 A/m2,α=0.5

溶液中离子传输仅由浓度梯度驱动，控制方程为菲克第二定律。

其中，Di为离子的扩散系数，i= Ox表示氧化物，i= Re表示还原物。

假设本体电解质位于无穷远处，x= ∞，离子浓度为本体浓度

在电极表面，x= 0，反应物被消耗，产物被生成。消耗/生成的速率和反应速率的关系如下

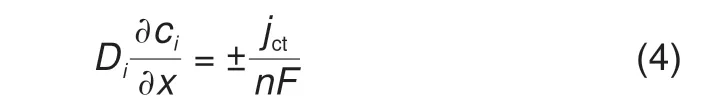
其中负号对应氧化物，正号对应还原物，氧化反应的电流定义为正电流，F为法拉第常数，n为转移的电子数，jct为法拉第反应的电流，一般通过Butler-Volmer方程计算[12-13]

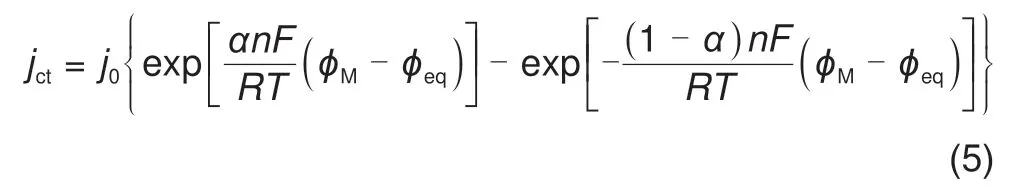
其中，j0为交换电流密度，α为电荷转移系数，F为法拉第常数，R为理想气体常数，T为温度，φM为电极电势，φeq为平衡电势，利用能斯特方程计算[12-13]

其中φ为标准平衡电势，γi为活度，c为表面浓度。

总电流除了反应电流，还有双电层电流jdl

其中，Cdl为双电层电容，一般依据Gouy-Chapman-Stern模型计算[12-13]

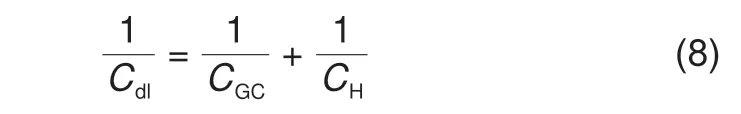
其中，CGC=ϵs/λD为Gouy-Chapman电容，ϵs为溶液本体的介电常数，λD为德拜长度。CH=ϵHP/δHP为Helmholtz 电容，ϵHP和δHP分别为Helmholtz 层的介电常数和厚度。

1.1 解析求解

对方程式(2)施加傅里叶变换可以得到频域的控制方程

傅里叶变换后的边界条件如下，本体x= ∞处

电极表面，x= 0处

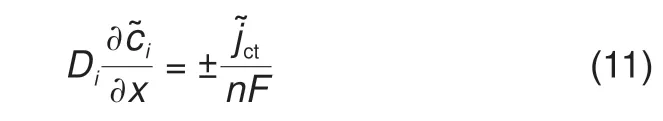
结合边界条件式(10)和式(11)，可以得到方程式(9)的解析解为

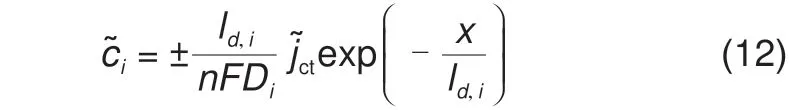
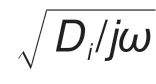
对Bulter-Volmer 方程做线性化展开，利用傅里叶变换可以得到

在稀溶液中，γOx=γRe= 1，把方程式(14)代入方程式(13)得到

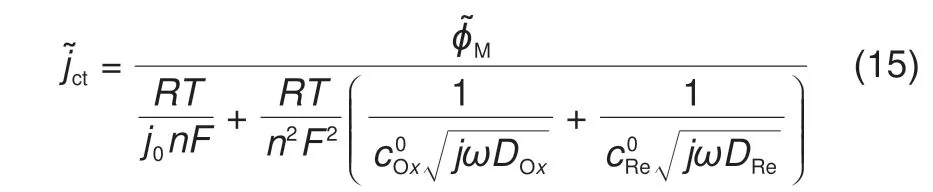
对方程式(7)做傅里叶变换，可以得到频域的双电层电流

1.2 时域数值方法

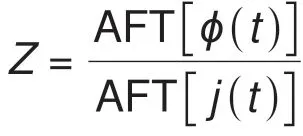
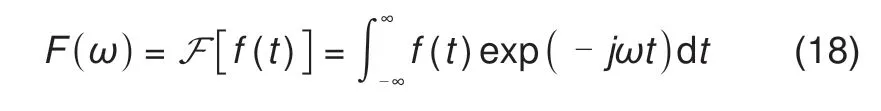
其中，f(t)为系统的时域响应信号，F为傅里叶变换算子。

对信号f(t)做线性插值处理可以得到

其中，σ(t)为归一化的阶跃函数。

把方程式(19)代入方程式(18)可以得到AFT 的表达式

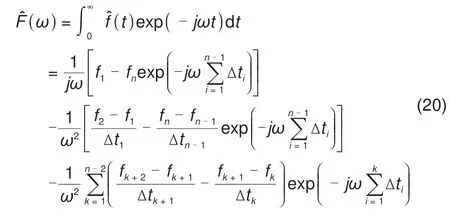
基于TSM 求解，再通过AFT 变换得到的EIS数值解和解析解的对比如图2(c)所示。在高频区域，数值解和解析解基本完全重合。低频区域的偏差略有增加，主要原因是有限元等方法求解微分方程会累计误差。

1.3 频域数值方法

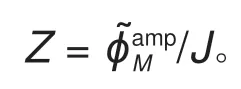
基于频域数值方法得到的EIS 数值解和解析解的对比如图2(d)所示(具体的MATLAB 程序放在支撑文件)。可以明显看到，数值解在整个频率范围内都和解析解很吻合，表明FSM 数值解精度较高。

2 求解案例

2.1 金属离子沉积反应体系

2.1.1 控制方程

溶液中离子的传输采用Poisson-Nernst-Planck(PNP)方程[14,20-22]描述。

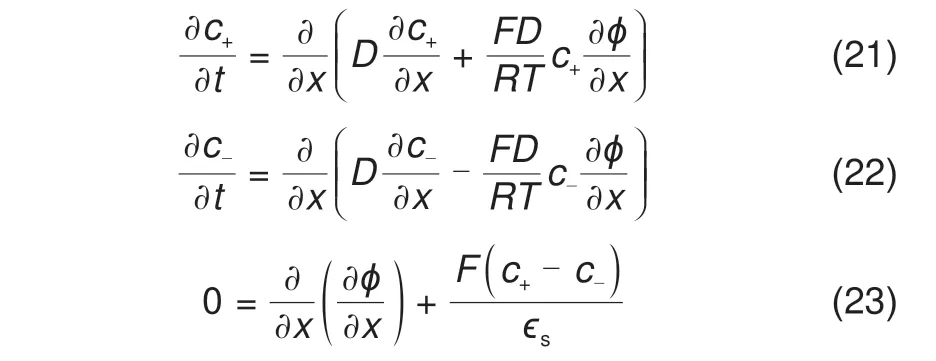
其中，c+和c-分别为阳离子和阴离子的浓度，D为扩散系数，ϵs为本体溶液的介电常数。

2.1.2 边界条件和初始条件

研究体系的边界分为左边界和右边界，左边界为Helmholtz 平面，x= 0 处。边界条件设置如下，对于阳离子，发生电子转移反应，阳离子通量和反应电流的关系见式(24)

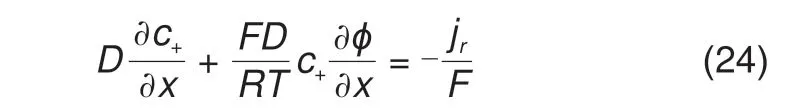
其中，jr为法拉第反应的电流，这里采用Frumkin-Butler-Volmer(FBV)方程[13]计算

其中，c0为阳离子的本体浓度，k0为反应速率常数，η为反应的过电势。η=φM-φHP-φ，φHP为Helmholtz平面处的电势。

对于阴离子，不参与反应，所以离子的通量为0

对于电势，从电极表面到Helmholtz 平面，电势线性下降[22]，所以电势的边界条件为

由于所有的电荷均为体电荷，Helmholtz 平面体积为0，不存在净电荷。因此，根据高斯定律，Helmholtz平面两侧的电势梯度满足如下关系

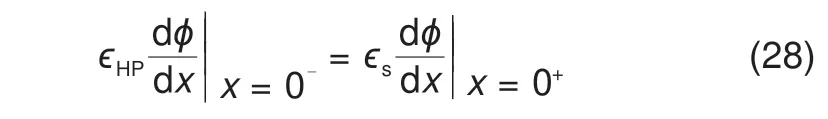
方程式(28)代入方程式(27)可得电势左边界的最终形式

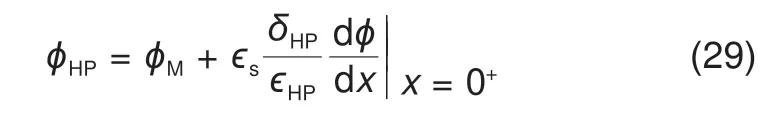
右边界为溶液本体，x=xb，电势为0，离子浓度均为本体浓度

结合边界条件对控制方程进行求解，我们可以得到零电荷电势(Potential of zero charge，PZC)下的解析表达式[10]

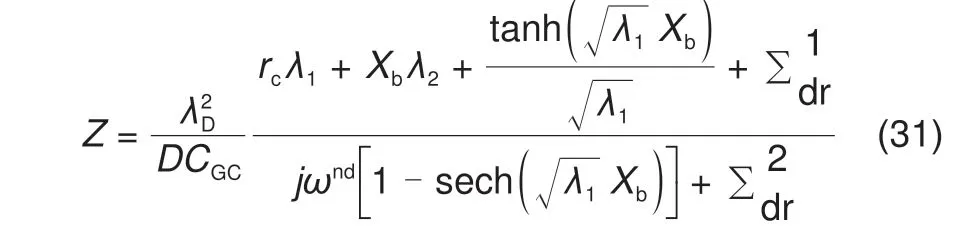
其 中，rc=CGC/CH为Gouy-Chapman 电 容 和Helmholtz电容的比值，ωnd=ω/D为无量纲的角频率，Xb=xb/λD为无量纲的电解质溶液厚度，λ1= 1 +jωnd，λ2=jωnd，和为沉积反应相关的变量。

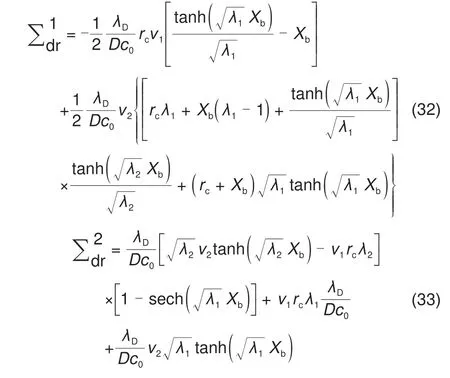
其中，ν1=k0{αexp(αΠ0)+(1-α)×exp[-(1 -α)Π]0]}，ν2=k0exp[ -(1-α)Π0]，Π0=(--φeq)F/RT为稳态的过电势，上标0 表示该变量为稳态变量。

2.1.3 数值求解

需要注意的是，在金属沉积反应中，边界条件中严格考虑了双电层的存在。因此，双电层电流不能再以Cdl为常数进行计算，而应该从电荷量求导去计算[22-23]

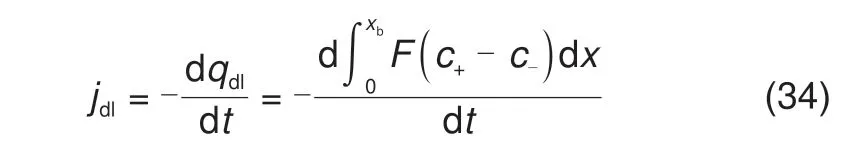
其中，qdl表示双电层中积累的净电荷量，负号表示积累的电荷和电极所带的电荷相反。

总电流的表达式如下

基于频域方程的数值求解则先要对控制方程和边界条件做傅里叶变换，具体的计算详情这里不再赘述[22-23]。频域下的控制方程(这里只考虑PZC下的情况)如下

在x= 0处，频域下的左边界条件为

在x=xb处，频域下的右边界条件为

2.1.4 三种方法结果对比

图3(b)～(d)依次为金属沉积反应EIS 解析解，时域数值方法的EIS数值解与解析解的对比，和频域数值方法的EIS 数值解和解析解的对比(具体的MATLAB 程序放在支撑文件)。需要注意的是，这里的解析解和数值解都只适用于PZC[22-23]。对于非PZC下的求解，初始条件不再满足均匀假设，离子浓度和电势均存在分布。特别是在双电层中，电势梯度和浓度梯度极大。笔者尚未看到有相关研究在考虑界面反应和双电层的条件下，自洽求解了非PZC下的EIS。

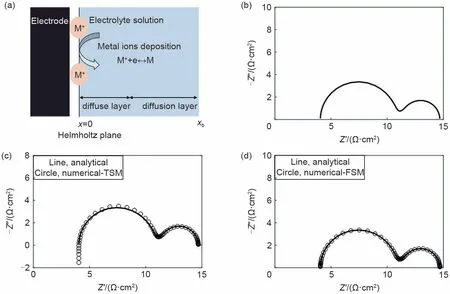
图3 (a)金属离子沉积反应电极/电解质溶液界面示意图；(b)EIS解析解的Nyquist图；(c)时域数值方法的EIS数值解与解析解的对比；(d)频域数值方法的EIS数值解与解析解的对比。频率范围为105～10-1 Hz。其余参数如下：c0 = 0.1 mol/L，D = 1 × 10-12 m2/s，k0 = 4 × 10-4 mol/(m2·s)，α = 0.5Fig.3 (a)Schematic diagram of electrode/electrolyte solution interface with metal ion deposition reaction;(b)Nyquist plot of EIS analytical solution;(c)Comparison of numerical and analytical solutions of EIS based on TSM numerical method;(d)Comparison of numerical and analytical solutions of EIS based on FSM numerical method;Frequency range is 105～10-1 Hz.Other parameters are as follows:c0=0.1 mol/L,D=1×10-12 m2/s,k0=4×10-4mol/(m2·s),α=0.5

从图3(b)解析解的结果可以看出，EIS 由高频反应半圆和低频扩散半圆构成。解析解作为精确解，用来评价不同数值方法求解EIS 的精度。图3(c)为时域方法的数值解和解析解。二者在中低频区域吻合较好，高频区域数值解出现感抗行为。从笔者的经验来看，主要是因为计算双电层电流采用的数值积分及微分存在较大的误差，进而导致高频感抗的行为。图3(d)对比了频域方法的数值解和解析解。不管是高频还是低频，数值解和解析解均很好吻合，表明数值解精度较高。

从三种方法对比结果可以得出，解析解避免了数值求解微分方程，因而精度最高。但解析解往往需要大量数学运算，才有可能推导出复杂体系的解析EIS。相比之下，数值解借助有限元等方法，可以直接得到体系的EIS数值解。对比不同数值方法的结果，可以得出，频域数值方法的EIS数值解精度较高，而时域数值方法的EIS数值解，低频区域精度较高，高频区域精度较低。因此，笔者建议优先选取频域数值方法计算EIS。

2.2 单价离子和多价离子阻抗的对比

金属离子沉积反应中，常见的离子价态为一价、二价和三价。图4 对比了不同价态离子的EIS(具体的MATLAB程序放在支撑文件)。其中，图4(a)和(b)分别为TSM 数值方法和FSM 数值方法的结果。在TSM 数值方法的EIS 结果可以看出，高频仍然存在感抗特征，其余部分和FSM 方法的结果一致，这也说明了FSM 方法的求解精度更高。对于不同价态的离子，在保持其余参数不变的情况下，离子价态越高，阻抗越小。主要原因在于，一方面FBV方程中考虑离子价态后，反应电流极大地增加。另一方面，通过积分电荷量计算的双电层电流也增加。因此，总电流极大的增加使得高价态离子的EIS减小。但需要注意的是，对于真实的研究体系，不同价态离子的动力学参数往往差别较大，读者需要结合实验标定相关参数，然后利用模型去拟合和解析实验数据。

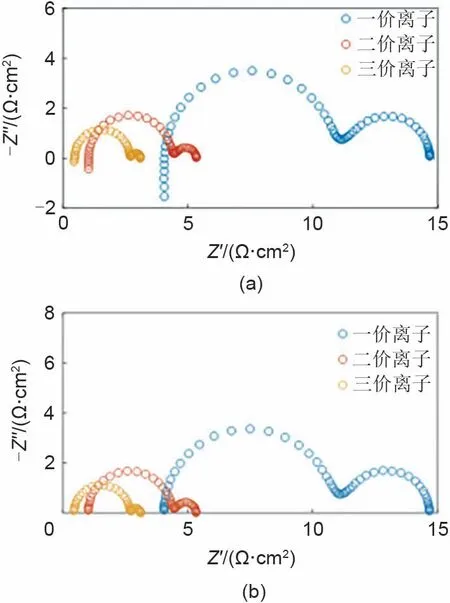
图4 (a)基于TSM数值方法的EIS结果对比；(b)基于FSM数值方法的EIS结果对比(除考虑不同离子价态外，其余参数均与图3 保持相同)Fig.4 (a)comparison of EIS results based on TSM numerical method;(b)comparison of EIS results based on FSM numerical method(Except for different ion valence states,other parameters remain the same as Fig.3 )

3 三种方法优缺点对比

图5对比了三种求解方法的优缺点。其中，解析求解优点在于物理含义清晰，易于分析高低频的渐进行为。缺点在于推导复杂，复杂体系难以解析求解。数值方法优点在于求解简单，无复杂推导。缺点在于计算耗时。其中，时域数值方法求解精度低于频域数值方法。但频域数值方法无法获得时域信号，难以有效判断中间变量的正确性。

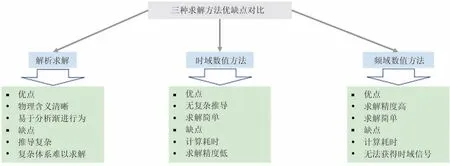
图5 三种求解方法优缺点对比Fig.5 Comparison of advantages and disadvantages of three solving methods

4 结论和展望

本文简要介绍了EIS 物理模型常见的三种求解方法：解析求解，时域数值方法和频域数值方法。随后结合具体的例子对比了不同方法的优缺点，得到的主要结论如下：解析解精度最高，但一般只适用于PZC 条件；对于非PZC，考虑双电层的条件下，无法求出解析解。对于数值解，优先推荐频域数值方法，精度较高且没有高频感抗行为。

为拓宽EIS在电化学中的应用，尚有很多工作值得开展。

（1）本文的解析解和数值解都只适用于PZC条件，对于非PZC下的EIS求解，笔者尚未看到有相关研究。如何自洽求解非PZC下的EIS是一个值得研究的课题。

（2）本文只考虑了单电子转移的反应，而燃料电池、电解水等电化学装置中的反应均为4电子和2电子反应。分步考虑电子转移反应，建立微观动力学模型，再计算EIS对于理解反应速控步骤，辨析反应机理等至关重要[24-25]。

（3）本文仅考虑了一维平板电极情况，而真实的研究体系多为粗糙界面、团聚体颗粒和多孔电极。Song等人[26]和Kant等人[27-29]的研究表明，几何效应对EIS响应有很大的影响。