异形截面立体编织的锭子轨道设计方法
孙志宏, 方 涛, 王振喜, 邵国为, 徐 昌, 王 兵
(1.东华大学 纺织装备教育部工程研究中心, 上海 201620;2.航宸石家庄新材料科技有限公司, 河北 石家庄 051430)
三维旋转编织成型工艺复杂,比二维编织有更多的叶轮和锭子,其锭子轨道设计也不局限于单条轨道,而是多条轨道相互交织。采用这种方法生产出的异形截面编织物作为复合材料预制体,有着优异的力学性能,在汽车、航天航空和军事领域都具有广泛的应用前景。
对于编织轨道的设计和锭子的排布方案,大多基于经验设计而效率低下,其基本的理论还不够完善。早在20世纪,Berger[1]在无结网编织的专利中提出轨道开关的变换机制;Laourine等[2]在文献[1]基础上,通过叶轮阵列排布,并且在所有轨道交叉的地方增加轨道变换装置,最大限度地提高了锭子运行的灵活性和编织物截面形状的多样性;文献[3-5]综合性地介绍了三维编织的种类和原理,并对三维织物轨道排布进行了分析,预测不同的轨道排布形式对纱线浮长的影响;Potluri等[6]研究了三维编织物的织造过程,以及锭子数量和转速对编织物结构的影响;Tolosana等[7]发明了一个Braid3DTex的软件系统,该软件能够很好地对编织过程进行数值模拟,但是在轨道设计和锭子排布方面无法做出有效的提示;Yu等[8]以薄壁织物为研究对象,提出了薄壁织物分支处防止锭子干涉的约束条件;Du等[9]通过建立数学模型对多层连锁的轨道进行研究,但其通过减少锭子数量解决锭子干涉的方法降低了机器的利用率。
为了提高异形截面编织物的轨道设计效率,本文建立多轨道交织的数学模型,探索研究更加通用的异形截面编织物的轨道设计方法和锭子排布方法。
1 三维旋转编织的基本原理
旋转式编织工艺来源于“Maypole”[10]式编织工艺,在编织过程中,锭子在旋转叶轮的拨动下沿着预定的轨道运动,锭子之间的相互交错运动使其携带的纱线产生交织,从而形成编织物。图1(a)是笔者课题组研制的立体旋转编织机[11],在轨道交叉处有变轨转盘,如图1(b)所示。锭子运动到交叉处时,可由变轨转盘的状态决定其是继续在原叶轮槽口中,还是进入相邻的叶轮槽口中。通过改变变轨转盘的状态,可在同一台机器上生产出不同截面的织物。

图1 异形截面立体织物的编织机和变轨转盘状态
异形截面立体织物的编织通常会有多个锭子同时运动,避免锭子运动时的相互碰撞是设计时需要考虑的关键问题之一。锭子交换原理如图2所示。由图2可知,同时进入P0点的锭子序列有且只有两条,分别为序列A和序列B,锭子随着叶轮旋转在轨道P0处相遇,但在P0处至多只能有一条序列上有锭子,叶轮上空出来的槽口用于相邻叶轮之间交换锭子。
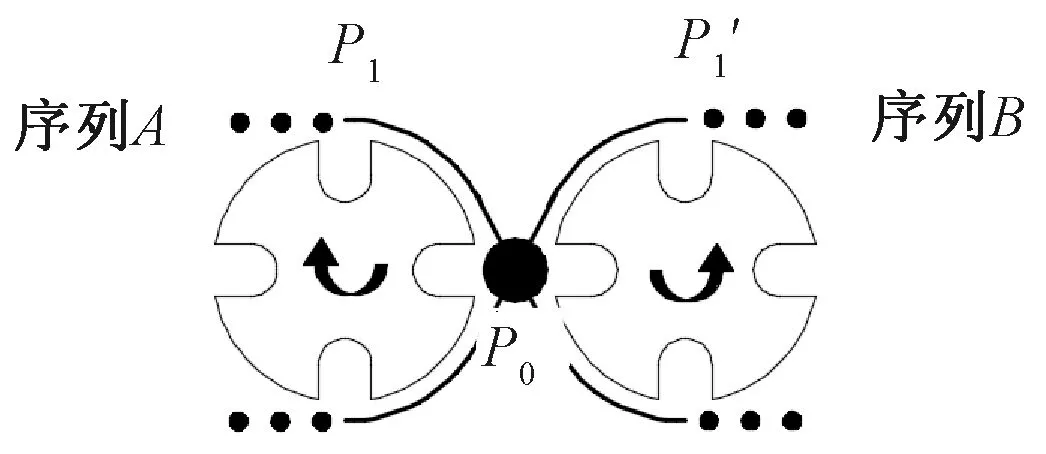
图2 锭子交换原理
如果序列A在t0时刻经过P0点的槽口携带锭子,那么序列B在t0时刻经过P0点的槽口一定不携带锭子。再经历时间Δt之后,P1点和P'1点的槽口将运动到P0点,所以在前一时刻,P1点和P'1点最多只有一个位置的槽口携带锭子。以P0点为起点,采用“1”和“0”(“1”表示槽口携带锭子,“0”表示槽口不携带锭子)表示锭子的携带情况,则序列A和序列B可能的状态如表1所示。两序列相同位置的槽口含锭子状态可分为三类:第一类是槽口锭子处于互补状态,如状态1、2、3和4;第二类是槽口锭子都为空的状态,如状态5;第三类是组合状态,如状态6和7。

表1 序列A和B槽口状态
在实际的编织过程中,为防止锭子的干涉,同一轨道上的锭子通常采用周期排布规律,根据表1中所示的锭子序列的基本状态组合,可以得出不同周期的锭子排布规律,如表2所示。值得一提的是,这种锭子序列的周期性排布方式,原序列和互补序列其实是同一序列,只是进入到同一个槽口相差W×Δt的时间,Δt为叶轮转过一个槽口的时间,W记为该排布规律的错位数。如序列A“1010010110100101…”其互补序列B为“0101101001011010…”,序列A在随着叶轮转动4个槽口之后,便和序列B的当前状态一模一样,该序列的错位数W为4。

表2 锭子排布规律
2 锭子排布方案分析
2.1 多条轨道闭环交织分析
锭子的干涉通常发生在轨道的交叉处。本文以轨道交叉点处的锭子序列状态为研究对象,再推广到一般情况。以排布周期是8、排布序列是“10100101”的锭子排布规律为例,绘制两条轨道在交点处的锭子状态,如图3所示,其中序列A的部分序列在t0时刻为“…10100101…”,序列B的部分序列在t0时刻为“…01011010…”。将两锭子序列拉直,如图4所示。
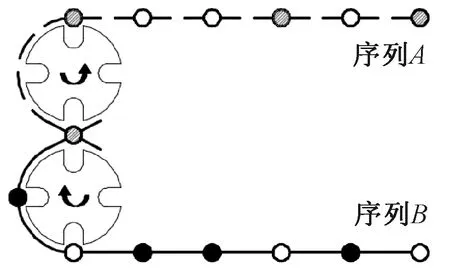
图3 交点处锭子排布
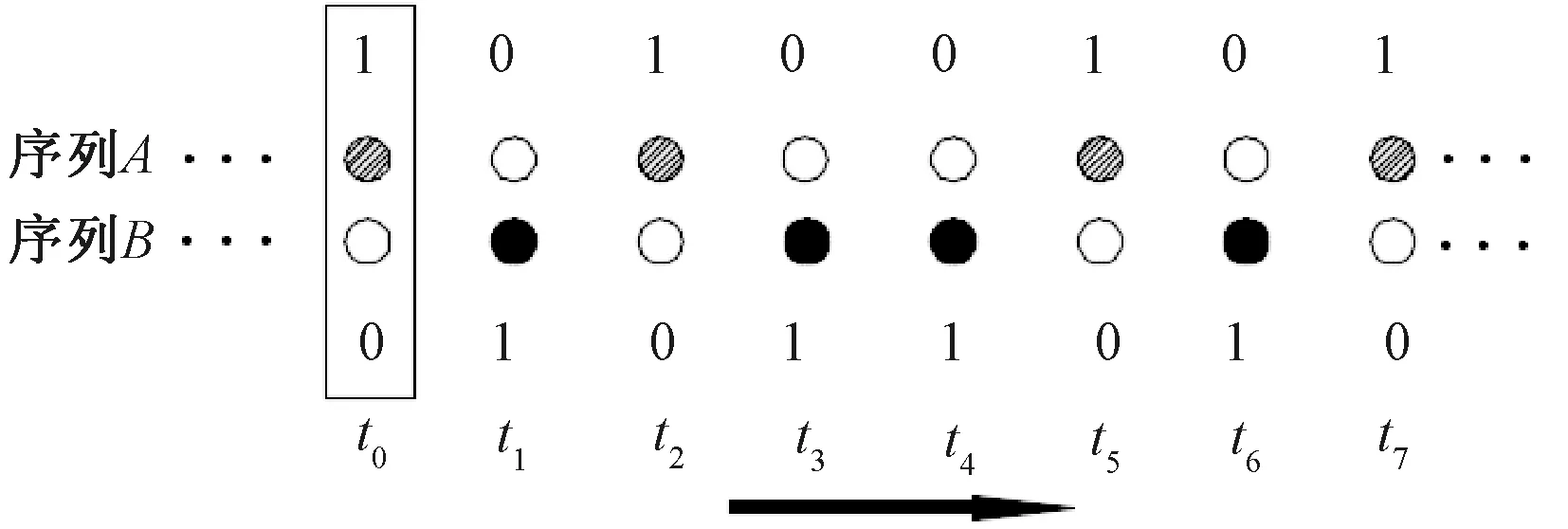
图4 交点处锭子序列拉直处理
图4中的矩形框标注的状态是图3中两叶轮交点处的状态,记此时为t0时刻,经过Δt时间后,交点处的状态随着叶轮的转向(图中序列向右的方向)移动一个槽口位置,到达t1状态,再经历6×Δt的时间,最终到达t7状态。由于锭子采用周期排布(此示例中周期为8),因此在任意时刻,交点处的状态必为t0~t7时刻中的一个,只要两条锭子序列在交点处错开相应的位数,其在运行的过程中就永远不会发生干涉。
在实际立体织物的编织过程中,轨道较为复杂,通常由多条轨道拼接而成,这样会在轨道之间产生多个交点。多个交点之间相互的制约关系给锭子排布带来了更大的困难。取某立体织物编织轨道中的4条轨道片段,其中,A、B、C、D为两条轨道之间的交点,n1、n2、n3、n4分别为4条轨道在两个交点之间的槽口数,如图5所示。根据两条轨道在交点处互补不干涉的原理,可以设计出轨道1和轨道2在B点不干涉、轨道2和轨道3在C点不干涉、轨道3和轨道4在D点不干涉的轨道排布方案。在B、C、D点不干涉的约束条件下,已经确定了4条轨道的排布,而轨道4和轨道1在A点再一次出现相交,轨道形成了闭环,那么A点处是否会出现干涉则无法再一次使用互补原理判断。在立体编织物设计时,多轨道交织形成闭环的情况非常多。研究多轨道闭环交织不干涉是解决立体编织物轨道设计的重要部分。
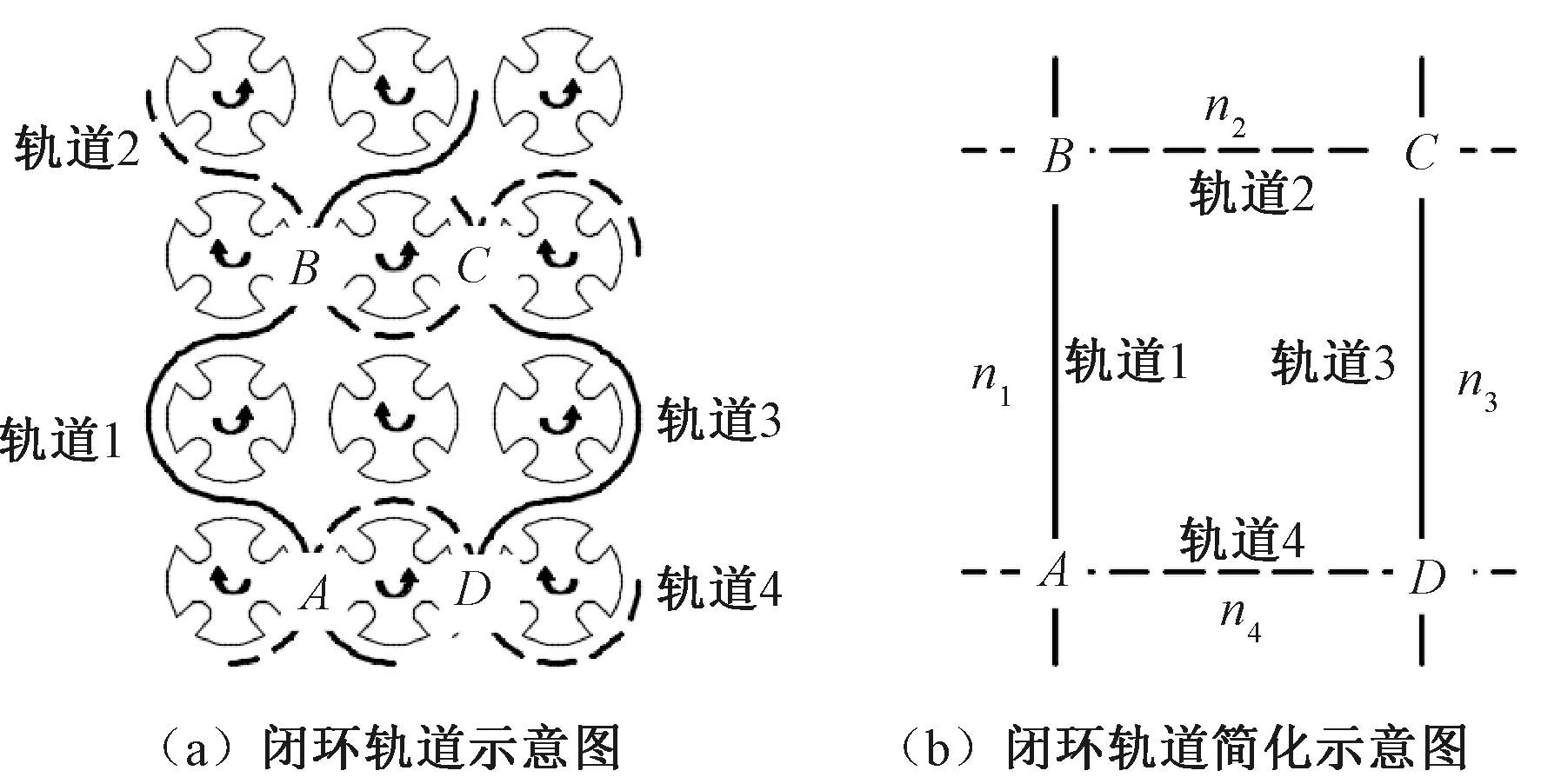
图5 闭环轨道及其简化图
为了方便描述,采用图5(b)中的简化轨道进行分析,且锭子的排布周期为T,错位数为W。周期为T的排布序列,每个槽口的锭子状态可能有T种。记槽口在某时刻的状态为

式中:x为槽口序号,x=1,2,…。假设在t0时刻轨道1在A点的状态为
S1A=S(φ)
(1)
式中:φ为轨道1在A点的初始相位,且φ=1,2,…,T。轨道1在A点和B点之间相差n1个槽口,因此,t0时刻轨道1在B点的状态为
S1B=S(n1+φ)
t0时刻轨道1和轨道2在B点交叉,因此,两者在B点的锭子排布时序应满足互补关系,即轨道序列在相位上相差W,轨道2在B点的状态用函数关系可表示为
S2B=S(n1+φ+W)
以此类推,在t0时刻,轨道2在C点的状态为
S2C=S(n1+n2+φ+W)
轨道3在D点的状态为
S3D=S(n1+n2+n3+φ+W×2)
如果不考虑轨道4和轨道1在A点相交,那么轨道4从D点开始,经过n4个槽口之后,在A点的槽口状态满足:
S14=S(n1+n2+n3+n4+φ+W×3)
(2)
根据两条轨道交点处的轨道状态应该互补的原则,式(1)和(2)中状态函数自变量的取值应相差n×T-W,方可保证轨道4和轨道1在A点相交且不干涉,由此得到:
n1+n2+n3+n4+φ+W×3-φ=n×T-W
化简得:
n1+n2+n3+n4=n×T-4×W
(3)
由上述分析可知,如果多条轨道相交形成闭环,闭环上的槽口数须满足一定的关系,如式(3)所示。其中“4”代表该闭环包含的轨道片段数量,记为K,则闭环上的轨道含槽口总数M为
M=n×T-K×W
(4)
当K=1时,仅有一条轨道自身交叉,形成两个交叉点P1和P2,锭子排布周期T=8,错位数W=4,如图6所示。由图6可知:在P1点的左侧,有一个单条轨道形成的闭环,n=1,环上经过的总槽口数等于1×8-1×4=4,满足式(4);P1点右侧有两个单条轨道形成的闭环,n=2,轨道经过的槽口数满足2×8-1×4=12,仍然满足式(4)。P2点的分析方法和P1点类似,不再赘述。

图6 单条轨道自身交叉
此结论可以用于复杂立体编织时轨道设计合理性的自动化检验,通过寻找轨道中的各个闭环并计算其是否满足不干涉约束条件,可快速进行编织轨道的设计。
2.2 自动化检验程序设计
为了便于进行多轨拼接编织工艺中轨道设计及锭子排布,本文采用有向图[12]的结构表达轨道交叉点及槽口数,然后将该有向图转换成邻接矩阵并进行运算。
在旋转编织工艺当中,主轴总是朝着一个方向旋转,因此每个叶轮的旋转方向是唯一的。每个锭子的走向由携带锭子的叶轮旋向决定,因此每条轨道上的锭子在两点之间的走向是单向且唯一的,故图7所示轨道槽口之间的关系可用如图8所示的有向图来表示。
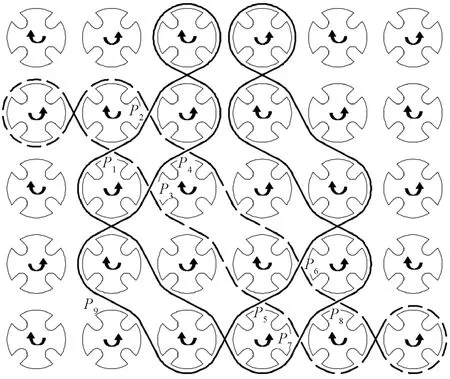
图7 编织轨道实例

图8 轨道的有向图表示
将不同轨道之间的交点和各交点之间的轨道含有的槽口数作为研究对象。在图8中,用P1、P2、P3…PN表示不同轨道的交点,作为有向图的顶点,与顶点相连的每条边上标记的数值称为权值,表示两个交点之间轨道含有的槽口数。有了交点和槽口之间的关系,便可以定义矩阵G来描述它们之间的关系,其表达式如式(5)所示。
(5)
式中:
通过编制程序可计算出轨道中所有的回路及判断每条回路所经过的槽口总数是否满足约束条件,其具体过程为:当P点是当前被访问的轨道交点时,P'是即将要访问的轨道交点,在对P做过访问标记之后,选择一条从P出发的未检测过的边(P,P'),如果发现顶点P'已经被访问过,则重新选择另一条从P点出发未检测过的边,否则沿着边(P,P')到达未曾访问过的P',对P'访问并将其标记为已访问过,然后从P'开始访问,直到搜索完从P'出发的所有路径,重复上述过程,直到出现某个顶点和第一个顶点相同,输出保存顶点信息,记为一条回路,并计算回路的槽口信息是否满足约束条件,给出提示信息。轨道回路计算流程框图如图9所示。
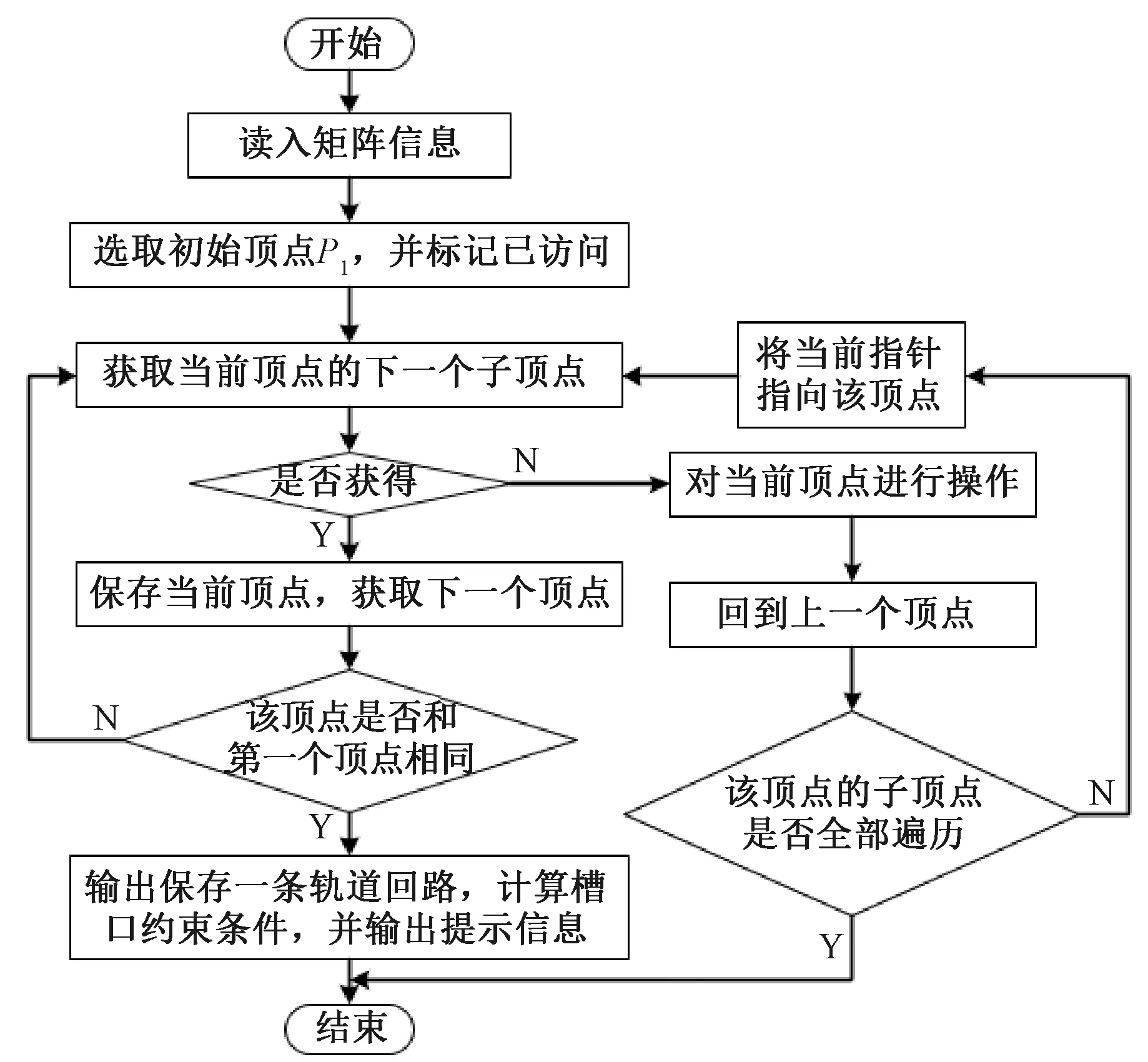
图9 轨道回路计算流程图
图7所示的两条锭子运行轨道之间有多个交点,将图7中的信息转换成计算机可以直接读取的矩阵如式(6)所示,计算每条回路是否满足不产生干涉的约束条件。计算结果提示,P1P7P5P3P1、P1P7P5P9P3P1、P1P7P5P3P4P2P1、P1P7P5P9P3
P4P2P1、P1P7P8P6P5P3P1、P1P7P8P6P5P9P3P1这几条轨道不满足槽口约束条件,且所有轨道都包含轨道片段P1P7。根据这样的信息,可以对轨道排布进行调整,调整后的轨道设计如图10所示,对其再次进行计算,可验证所有轨道都满足槽口总数的约束条件。

图10 调整后的轨道

(6)
3 三维立体编织的轨道布置方式
本文第2节提出了编织轨道合理性的检验方法,但是实际设计编织轨道时,还应遵从更加简易的规则。在三维编织机上,每个叶轮的槽口数都是4,但是采用等效叶轮的方式可以等效出8槽口叶轮。编织平台上基本的4槽口叶轮如图11(a)所示,其中间的两个叶轮可以等效成一个8槽口叶轮,如图11(b)所示。
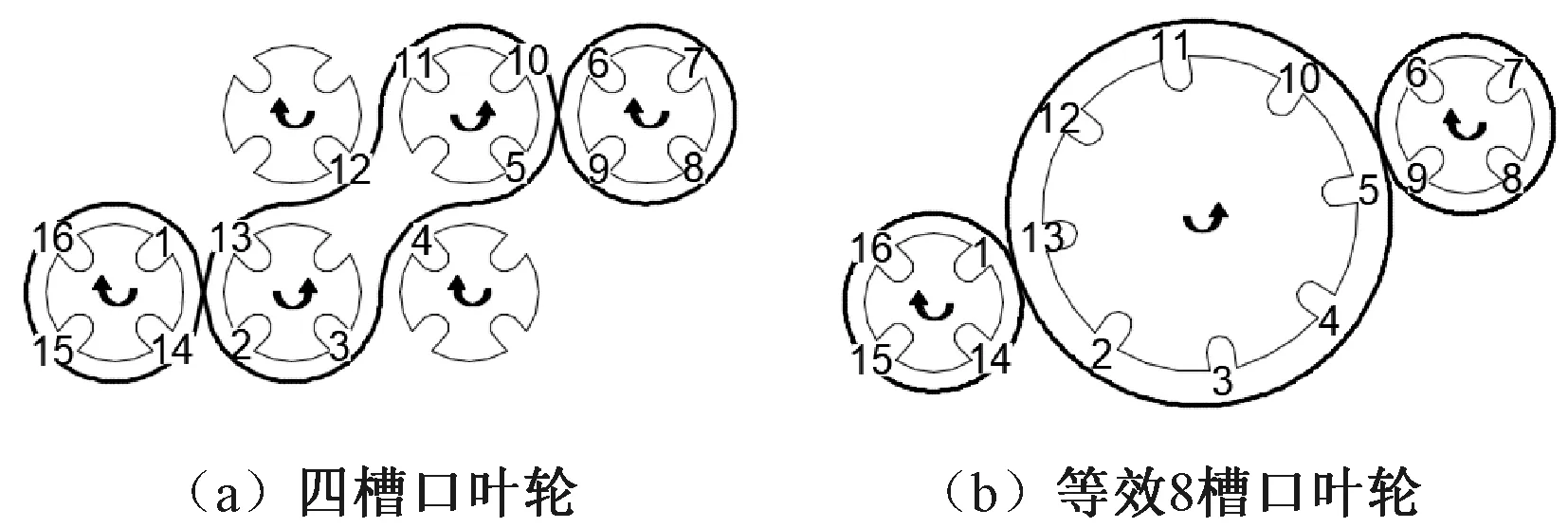
图11 等效叶轮
对每一条轨道都采用两端分别为4槽口叶轮,中间全部为8槽口叶轮,锭子排布周期为8,错位数为4的“10100101”锭子排布序列,单条轨道不会发生干涉。按照这种轨道布置方式,可以灵活地延长并形成各种走向的轨道,如图12(a)所示。通过多条轨道组合,能够设计出不同截面立体织物的编织轨道,且经过计算可知,通过这种轨道组合形成的立体织物编织轨道不会发生干涉。在立体织物设计过程中,可优先选取此种轨道设计方法。图12(b)所示是由3条不同形状的轨道组成的T形截面立体织物编织轨道,通过本文第2节的程序计算得出,采用锭子循环周期为8和错位数为4的锭子排布规律不会发生干涉,排布方式也如图12(b)中所示,并采用图1(a)中的立体编织机进行编织试验,所得织物如图13所示。

图12 单条轨道设计形式和轨道组合示意

图13 T形截面立体织物
4 结 语
本文基于旋转编织的基本原理,分析得到了多条轨道交织时轨道闭环经过的总槽口数应该满足的约束条件,并通过采用邻接矩阵表达轨道信息的方式,提出了轨道设计合理性的计算评价方法,对干涉位置进行提示,减少了轨道设计的工作量。针对立体旋转编织平台提出了一种8槽口等效叶轮,并利用8槽口等效叶轮和4槽口叶轮组合的轨道设计,更加快速地设计出了立体编织物的编织轨道,对异形截面三维旋转编织物的设计有指导意义。

