三维突变截面预制件的编织工艺
邵国为, 孙志宏, 王振喜, 王 兵, 李雪清
(1.东华大学 a.机械工程学院,b.纺织装备教育部工程研究中心, 上海 201620;2.航宸石家庄新材料科技有限公司,河北 石家庄 051430;3.中国纺织机械协会, 北京 100028)
三维编织技术能够在厚度上增强复合材料,并且能够适应各种复杂截面形状的立体织物制备工作[1],例如,从管状结构到实心立体结构,从薄壁工字梁到厚壁火箭喷嘴结构。采用三维编制技术制得的复合材料的纱线交织模式和结构横截面形状多种多样。这些优势使三维编织复合材料在航空航天工业、医疗装备等特殊领域得到日益广泛的应用[2-5]。目前这些应用涉及的三维编织结构件均是等截面结构或渐变截面结构,而三维突变截面结构的编织工艺尚有困难。
专家学者先后提出多种异形截面结构件的编织工艺设想,目前主要有行列式法和旋转法。行列式法在变截面编织成型工艺上的应用主要集中在渐变截面结构织物的编织[6-7],通过改进携纱器[8-10]的结构来达到渐变截面结构织物编织的目的,生产效率得到提高,但是改进的携纱器尺寸过大,致使编织相同尺寸的织物时参与编织的纱线数量大大减少。目前的三维旋转编织机采用步进式旋转法,纱锭每次旋转至纱线的交叉点处时都需要停转判断交叉点处是否需要交换锭子,编织效率较低。Schreiber等[11-12]开发了两代六角形三维旋转编织机,并拼接了各种等截面结构的三维编织织物的轨道,但未涉及可实现变截面三维织物的编织工艺。Tsuzuki等[13]应用角轮式三维旋转编织技术实现了“J”型、“T”型与工字型等多种等截面三维织物的编织。Yordan[14-15]分析了等截面三维编织织物的轨道拼接及其锭子不干涉布置方式,同样未提及变截面编织方面的具体成型工艺。Yu等[16]研究了基于角轮式的二维旋转编织技术及编织成型过程中的锭子不干涉理论。袁天行等[17]分析了无结网网状织物的编织工艺,但是其织物截面结构为圆形结构间的突变。
以上所述编织物均可在1台方形旋转编织机上实现。方形旋转编织机为特种形式的角轮式三维旋转编织机,其轨道花盘为方形,且叶轮和变轨转盘数量更多。本文运用轨道变换法在方形旋转编织机上拼接成轨道,采用“10”锭子排布方式避免锭子间发生干涉;分析轨道拼接机理并对突变截面三维编织预制件的纱线路径进行仿真,最后进行实物编织。
1 基于轨道变换法的轨道拼接机理
基于轨道拼接技术和旋转式编织技术研发的多功能编织试验研究装置如图1所示。其采用64个4槽口角轮,以8×8阵列布置在轨道花盘上,角轮为锭子运动的驱动源件。112个变轨装置分布在每相邻两个叶轮中间以实现轨道的拼接变换。具体流程为:先根据织物截面形状计算锭子走向,避免锭子发生碰撞;然后在计算机程序的控制下实时变换轨道编织方案,实现各种截面三维织物的编织成型。此装置不仅可以编织三角形、矩形、口字型等截面结构的定截面和薄壁织物,还可在不停机的情况下编织三维渐变截面以及三维突变截面结构织物。

图1 三维方形旋转编织机及其编织示意图
图2为2行×2列(2×2)角轮布置的轨道拼接示意图,其中:带圈数字表示图1中的锭子,带旋转符号的十字符号表示角轮,角轮四周的直线代表状态为0(轨道路线堵死)的变轨转盘。初始位置时变轨转盘的状态全部为0,即轨道全部断开,锭子只能在角轮槽口内绕角轮自转,此时将图2(a)内部4个变轨转盘的状态全部变为1(轨道路线重新连接),同时角轮驱动锭子旋转角轮45°(见图2(b)),由于图2(b)所示的内部位置处轨道连通,锭子03、12、33与42分别转到相邻的角轮处(见图2(c)和(d))。若是需要将轨道路线堵死,将图2(d)中的角轮再旋转45°,并使图2(d)所示内部位置的变轨转盘状态重新变为0即可。

图2 2×2角轮布置的轨道拼接示意图
图2所示的2×2角轮布置轨道中锭子布置采用较为常用的“10”排布[14](见图3),锭子“10”排布表示锭子的排布周期为2,当周期内的锭子在第1个槽口处有锭子时记为“1”,在第2个槽口处没有锭子时记为“0”,然后依次循环进行锭子排布。由于锭子排布周期为2,因此轨道中不存在锭子干涉问题。

图3 基于轨道变换法的加纱示意图
2 基于轨道变换法的锭子运动过程
2.1 基于轨道变换法的纱线编织操作
图3为基于轨道变换法的加纱示意图,其中,“2×2”“4×4”为轨道花盘上的角轮排列形式,分别表示“2行×2列”“4行×4列”。对编织轨道花盘和变轨转盘做简化处理,并用两种颜色区分锭子。初始状态的锭子按照半满(每个角轮最多携带两个锭子)状态布置在每个角轮的槽口中,以确保有最多的纱线参与编织;初始状态时变轨转盘的状态全部为0(轨道全部断开),当角轮开始转动后,角轮槽口内的锭子只能绕所在角轮转动,使得该角轮上两个锭子各自携带的一根纱线相互缠绕。
执行编织任务时,根据预制件的截面形状将初始位置状态时相应截面形状内的变轨装盘状态变换为1(图3(b)~(d)),形成截面需要的轨道交叉形式,即截面形状内的轨道由断开状态变为连通状态,只需在角轮转动到初始状态时变换截面内相应位置的变轨转盘状态(采用舵机控制,舵机额定转速为6.16 rad/s),即可执行下一个编织任务(角轮的转速为6.19 r/min)。而预制件截面形状区域外的变轨装盘保持初始状态,其每个角轮上两个锭子带动相应纱线在角轮自转驱动下相互缠绕。
当编织横截面形状沿编织方向连续变化的织物时,只需在锭子运动至变轨转盘的45°方向(见图2(a))时,将截面形状区域内的变轨装盘状态变换为1(轨道连通状态)即可。
锭子进入变轨转盘位置前后的示意图如图4所示。当锭子处于变轨转盘区域外时,变轨转盘的转动不受限制(见图4(a));而当锭子处于变轨转盘区域内时,锭子就像销钉一样使变轨转盘与轨道花盘连接在一起无法转动(见图4(b))。因此,只有锭子运动至偏离变轨转盘区域时,变轨转盘才能自由旋转,轨道才能正常拼接。

图4 锭子进入变轨转盘所在区域前、后示意图
预制件截面形状逐渐缩小(减纱)的工艺流程与图3的加纱操作相反,其是将预制件截面形状区域外的相应变轨转盘的状态变为0,使区域外的轨道断开,从而减少参与预制件截面形状内编织的纱线,而预制件截面形状区域内的纱线相互编织成型,最终完成编织作业。
2.2 轨道变换过程中的纱线数量加/减规律
由图3可以看出,当三维编织物的截面形状逐渐增大时,每次增加的纱线数量根据所增加的参与编织的角轮数量而定。从初始状态变为编织2×2矩形(截面形状)三维织物时,增加3个角轮参与编织,则增加的纱线数量为6(增加参与编织的纱线数量)=2(倍数)×3(增加的参与编织的角轮数量)。以此类推,当编织截面形状逐渐增大的三维织物时,需要增加的纱线数量(N+)与增加的参与编织的角轮数量(nh+)的关系为N+=2nh+;当截面形状逐渐减小时,其每次减少的纱线数量为N-=2nh-,nh-为减少的参与编织的角轮数量。
3 突变截面编织实例
3.1 矩形-圆形-矩形截面三维立体编织工艺
图5为截面形状突变的三维编织试件。该突变截面不仅截面面积变化,截面形状(矩形-圆形-矩形)也在变化,其中上、下两个矩形截面面积相等。在编织过程中,试件在截面P1与P2之间的截面形状为矩形,截面P2与P3之间的截面形状为圆形,截面P3与P4之间为矩形。

图5 突变截面三维编织试件
图5所示的三维突变截面试件共有4个截面,其中,截面P2与P3分别为减纱和加纱截面,设定截面P1至P2之间编织的纱线数量为N0,N0=2nhr,nhr为截面P1与P2之间参与编织的角轮数量。当编织至减纱截面P2时,参与编织的纱线数量为N1,N1=2(N0-nh-),nh-为编织机编织至截面P2时,减少的参与编织的角轮数量。而编织至加纱截面P3时,参与编织的纱线数量为N2,N2=2(N1+nh+),nh+为编织机编织至截面P3时,相对于截面P2增加的参与编织的角轮数量。
3.2 纱线路径拟合
拟合前的突变截面三维编织预制件的纱线路径仿真图如图6所示。图6中三维变截面立体预制件中纱线的空间路径为折线,无法体现纱线之间的真实交织情况,且其矩形截面与圆形截面处的区别不明显。

图6 拟合前的突变截面三维编织预制件的纱线路径仿真图
基于MATLAB软件中的样条指令csaps(x,y,p)对图6所示的纱线空间路径进行平滑处理,其中,x、y为位置点坐标,p为权因子,0≤p≤1。
式中:w为权重,默认为1。D2f为样条函数csaps(x,y,p)在xi处的二阶导数,根据原始空间路径的x,y,z数值,分别将z与x、z与y拟合,其中p=1。
每条空间纱线中的z与x样条函数中三次多项式的系数用矩阵CPP表示。
从而得到表示每个样条曲线的多项式s(z):
式中:ai,bi,ci,di(i=1,2,…,7)对应7个分段三次多项式的系数。
然后,利用函数xi=ppval(csaps(x,z,p),zi)与yi=ppval(csaps(y,z,p),zi)分别对z与x、z与y进行插值处理。插值后的纱线轨迹曲线如图7所示。从图7(b)的投影视图A中可清晰分辨出突变截面三维编织预制件中的矩形截面与圆形截面。

图7 拟合后的突变截面三维编织预制件的纱线路径仿真图
编织完成后的预制件如图8所示,中间部分的减纱区域(圆柱体区域)存在未参与编织的纱线,可将这些纱线剪掉。由于减纱后三维突变截面编织预制件内部的纱线间仍为六面约束,预制件多余纱线的剪除不会对其整体使用功能产生影响[9]。

图8 突变截面三维编织物
3.3 三维突变截面编织织物整体尺寸计算
如图1所示的方形旋转编织机有64个角轮,按8×8排布在轨道花盘上。角轮采用直径为90 mm的四槽口角轮形式;变轨转盘的直径为37 mm,高度为27 mm;编织机的整体尺寸为1 200 mm×1 200 mm×1 800 mm;共有128根纱线纱线可以用于三维突变截面编织物的编织;每个携纱器携带的纱线长度为15 000 mm。在根据轨道变换法拼接而成的轨道中,锭子携带纱线在轨道中运动,参与三维突变截面预制件编织的纱线相互交织,从而得到三维突变截面预制件在挤塞条件下的宏观尺寸,涉及预制件的长度T与宽度W、纱线在挤塞条件下横截面的宽度2b以及任意两相邻的平行纱线的距离2a,三维突变截面编织物成型后的纱线横截面为菱形,此时满足a=b[18]。具体表达式如式(1)~(4)所示。
(1)
(2)
(3)
(4)
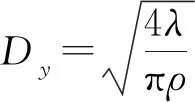
选用尼龙绳对三维突变截面织物进行编织,尼龙绳在挤塞条件下的截面为菱形形状[18],此时,其横截面的宽度为2b=3 mm,其截面面积为S=28.274 mm2。可得到三维突变截面编织物的矩形截面的长度和宽度为T=W=30 mm,圆形截面直径为25 mm。
4 结 语
提出一种可实现三维突变截面织物编织的轨道变换法,并以2×2角轮布置的轨道为例,分析基于轨道变换法的轨道拼接机理。2×2角轮布置的轨道中锭子布置采用常用的“10”排布,不需要对锭子之间进行复杂的干涉计算。 通过分析基于轨道变换法的锭子运动,给出了三维编织物截面形状突变时的加纱或减纱操作过程,得到了轨道变换过程中参与编织的纱线数量变化规律,即参与编织的纱线变化的数量始终是参与编织的角轮变化的数量的2倍。对三维突变截面编织物结构的纱线运动路径进行仿真,并在方形旋转编织机上进行编织。结果表明,基于轨道变换法的三维突变截面织物的编织工艺具备可行性,且操作过程简单。

