基于区间化参数的平面闸门主梁挠度可靠度分析

张迅炜，郑鼎聪，周建方

（河海大学机电工程学院，江苏常州 213022）

0 引 言

对闸门主梁进行挠度可靠度分析时，需要考虑3 个方面的因素。一是闸门主梁挠度的失效准则存在模糊性，即主梁的挠度失效并非按闸门设计规范（SL74-2020）［1］中所规定的，相对变形超过限值即绝对失效，相对变形小于限值则绝对安全。事实上，主梁从安全状态到失效应是一个逐步过渡的过程，而不是一个绝对边界。因此，常将主梁相对变形限值看作一个模糊变量。为使传统的可靠度计算方法仍适用于含模糊变量的主梁挠度可靠度分析，可采用当量随机化方法将主梁相对变形限值由模糊变量转化成随机变量。

第二个因素是闸门主梁的抗力R。当闸门主梁相对变形限值转化成一个随机变量后，抗力R也随之确定。由文献［2，3］可知，抗力R一般为对数正态分布，其数字特征主要受反映闸门主梁材料性能不定性的随机变量KM、反映闸门主梁几何尺寸不定性的随机变量KA、反映闸门主梁抗力计算模式不定性的随机变量KP以及相对变形限值的不定性K［w］的影响。KM、KA及KP可通过查阅文献得到，K［w］亦可通过计算求得，最终由误差传递公式可得抗力R的统计参数。至此，抗力R的分布类型及数字特征可知，故工作的重点在于研究第三个因素，即闸门主梁所受的荷载S。

在闸门主梁所受所有荷载中，静水压力对其可靠性的影响程度最大，故本文主要针对静水压力进行分析。目前，若要直接确定静水压力的随机分布尚有困难。由文献［4］可知，闸门作用水头与静水压力呈近似线性关系。因此，可通过对闸门作用水头进行分析获得静水压力的统计信息。然而，对闸门作用水头进行统计分析面临着数据不足的问题。由于基于有限的样本，难以建立闸门作用水头准确的概率模型，这使得可靠度分析的结果是否能够代表真实情况存在较大争议，该问题也在一定程度上限制了可靠性分析方法在闸门上的实际应用。

为此，笔者认为可对有限的闸门作用水头资料进行区间分析，将其均值及其标准差用区间量表示，并给出该区间包含参数真值的可信程度。此时，闸门可靠度分析由传统的全概率模型计算转为概率－区间混合模型计算。本文以丹江口水库某一平面深孔闸门为例，分别采用全概率模型及概率－区间混合模型分析闸门主梁挠度可靠度。结果表明，区间-概率模型分析结果包含了全概率模型的结果，并能给出相应的置信度，从而验证了静水压力的统计参数用区间变量表示的可行性。

1 静水压力统计分析

对闸门而言，最主要的荷载为静水压力，其大小通常用闸门作用水头来描述。目前，所能得到的统计资料大多是大坝的水头信息，因此，对闸门所受静水压力进行统计分析时，需将大坝水头的统计资料转化成闸门作用水头资料。闸门的作用水头HSG为：

式中：HS为大坝水头；H0为闸门孔口底槛对坝底高度，当大坝水头取设计值HSd时可得对应的闸门作用水头设计值HSGd。

由于所能得到的闸门作用水头的统计资料记录年份有限，以此为子样所求得的统计参数难以精确地描述大坝水头（即母体）的概率分布。因此，可采用参数的区间值，同时此区间包含参数真值的可信程度，即统计学中的置信区间［5］。

依据中心极限定理，在子样容量充分大时，子样均值趋向正态分布。此时的母体标准差σ是未知的，按照文献［6］，母体标准差σ未知时，在置信水平为1-α时的母体均值m的置信区间为：

置信水平为（1-α）时母体的标准差σ的置信区间为：

式中：S、n含义同前；(n- 1)与- 1)为卡方分布值。

为能够描述静水压力的不定性，结合式（1），可采用无量纲统计参数。即：

2 闸门主梁抗力分析

2.1 极限状态方程的建立

闸门主梁通常被简化为受均布荷载的简支梁，则其相对变形w为［7］：

式中：W为挠度；L为闸门主梁跨度；q为静水压力；E为闸门主梁的弹性模量；I为闸门主梁的截面惯性矩。

将其改写成一般式可得：

式中：S为荷载效应，S=q L2/8；C为与闸门主梁端部约束条件、跨度有关的系数，C=384/（40L）；EI为抗弯刚度。

依据闸门设计规范（SL74-2020），变形验算规定为：

由式（7）可建立闸门主梁正常使用极限状态方程为：

式中：［w］是闸门主梁相对变形限值。

在闸门设计规范（SL74-2020）中为一定值，参考文献［8，9］，认为［w］为一模糊量更为合理（下文中将规范中规定的闸门主梁相对变形限值用［w］K表示），其隶属函数为降半梯形分布（见图1），即：

图1 降半梯形隶属函数

式中：x1，x2为两个限值。

当x＜x1时，认为闸门主梁安全；x＞x2时，闸门主梁完全失效；x1≤x＜x2为过渡区，此时闸门主梁是否失效处于模糊状态，由文献［9］可知，露顶门x1=1/600，x2=1.1x1；潜孔门x1=1/750，x2=1.05x1。

由于结构模糊失效域μ(x)与结构模糊允许域互为补集，所以为升半梯形隶属函数：

采用文献［10］中的当量随机化方法，可将模糊量［w］转化为随机量，当量随机化后的均值及标准差为：

式中：x1与x2意义同上文。

在式（8）的极限状态方程中，荷载效应与抗弯刚度均在w中反映，与承载能力极限状态方程的表示不一致，为此，定义：

将式（6）代入式（8），并结合式（12）的定义，有：

上式与承载能力极限状态方程完全一致，可采用一次二阶矩法进行计算。

2.2 抗力的统计参数

极限状态方程式（13）中的抗力R可改写成一般的表达式：

式中：RK为相对变形达到闸门设计规范（SL74-2020）规定的闸门主梁相对变形限值［w］K时计算所得的抗力标准值；KP、KM、KA及K［w］分别为反映计算模式、材料性能、几何参数以及［w］不定性的随机变量。

抗力的不定性用无量纲统计参数KR来描述：

KR的统计参数可基于M、F及P的统计参数由误差传递公式推得，其平均值：

变异系数：

由（12）式可知，材料性能指的是钢材的弹性模量，目前国内统计量为KM= 1.0，δKM= 0.06；本文按文献［11］中有关规定对焊接工字钢截面统计参数分析的结果为KA=1.0，δKA= 0.022；由于闸门主梁是受弯构件，根据文献［12］，受弯构件计算模式不定性统计参数为KP= 1.0，δKP= 0.1。将相关数据代入式（11），可得露顶门［w］当量随机化后所得随机量的均值m=0.001 750，标准差σ=0.000 048 1；潜孔门m=0.001 367，σ=0.000 019 2。

此时，K［w］为：

变异系数：

由式（18）及式（19）求得露顶门K[w]= 1.05，δK[w]= 0.027 5；潜孔门K[w]= 1.025，δK[w]= 0.014 0。结合式（16）、式（17）及有关数据，可得闸门主梁抗力的统计参数见表1。

表1 闸门主梁抗力统计参数

参考文献［1，2］，闸门主梁抗力一般为对数正态分布。

3 概率—区间混合模型可靠度分析

带有区间变量Y的随机变量X从原空间映射到标准正态空间为：

对应的原极限状态方程在U空间的表达式为：

式中：Y为m维区间参数，Y∈［YL，YR］，YL和YR分别为区间参数的上下限。

由于区间变量的存在，原空间中的极限状态方程映射到标准正态空间后，将形成一带状区域（极限状态带），此时的可靠度指标β为一区间范围［βL，βR］，βL、βR分别为原点到带状区域两边界的最短距离，见图2。

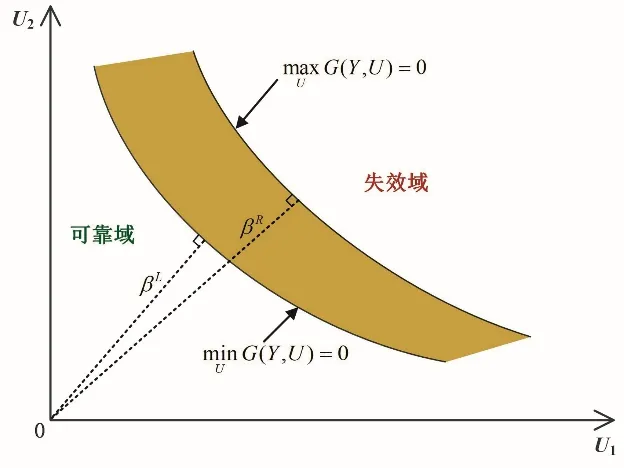
图2 极限状态带与可靠度指标

由文献［13］可知，若某一变量的累积概率密度函数CDF 关于其区间参数单调，则极限状态带的两边界必然对应着区间参数的上下限。区间参数可根据其对CDF的影响分为第1类区间参数和第2 类区间参数［14］。其中，第1 类区间参数是指CDF 的单调性仅与其参数本身有关，与随机变量无关，如正态分布中的均值μ；第2 类区间参数是指CDF 的单调性不仅与参数本身有关，且与随机变量相关，如正态分布中的标准差σ。

对于第1 类区间参数，受该类参数影响所形成的极限状态带的边界为光滑边界，易知极限状态带的边界与区间参数上下限的对应关系与CDF 的单调性及功能函数的梯度值∂G/∂Y有关。常见的CDF与第1类区间参数的单调性关系见表2。

表2 常见的CDF与第1类区间参数的单调性关系

极限状态带的边界与第1类区间参数上下限的具体对应关系见表3。

表3 第1类区间参数上下限与极限状态带边界的对应关系

对于第2 类区间参数，在具体计算过程中产生交叉分段的情况。因此，需在确定第1 类区间参数与极限状态带边界对应关系的基础上将该类区间参数的上下限代入试算，以获得可靠度指标上下限βL及βR。

4 算 例

丹江口水库一期工程的坝顶高程为162 m，最大坝高为97 m，相应的正常高水位为157 m。其中某一平面潜孔门的孔口底槛高程为113 m，主梁材料为Q235 钢。该水库1970-1999年共计30年的年最高水位资料见表4。

由于表4 中所给数据为水库水位，最终需将其转化为闸门作用水头数据。结合式（1）可知，闸门作用水头=水位－闸门孔口底槛高程。这样即可直接对闸门作用水头进行统计分析。由于可靠度分析中常见的分布类型包括正态分布、对数正态分布及极值Ⅰ型分布，故假设闸门作用水头服从上述三种分布，并在α=0.05 的置信度下采用K-S 检验法进行检验。检验结果见表5。

表4 丹江口水库年最高水位统计表

表5 闸门年最高作用水头分布检验

表5 中的结果表明，该闸门年最高作用水头不拒绝正态分布及对数正态分布，但拒绝极值Ⅰ型分布。其中，正态分布的统计量小于对数正态的统计量。因此，采用正态分布对闸门年最高作用水头分布进行拟合的效果最佳。

由于样本数量的限制，难以精确地得到闸门年最高作用水头均值与标准差。因此，采用参数的区间估计。依据式（2）及式（3）可求得该闸门在置信水平为0.95 时，年最高作用水头均值mHSG的区间及年最高水位标准差σHSG的区间为：mHSG∈(38.5，41.65）；σHSG∈（3.346，5.648）。根据《水利水电工程结构可靠性设计统一标准》（GB 50199-2013）［15］，对于正常使用极限状态，作用的分项系数应取为1.0，因此设计水位即为正常高水位。据此可推得闸门作用水头设计值=正常水位－孔口底槛高程=44 m。

按式（4）可得静水压力的无量纲统计参数K，其均值mK的区间及标准差σK的区间为：mK∈(0.875，0.947）；σK∈(0.076 0，0.128 4）。由于闸门作用水头用正态分布的拟合效果最佳，因此，可认为静水压力服从正态分布。

抗力的统计参数见表1。依据上文中的概率—区间混合模型可靠度分析方法，可知mK=0.875 对应极限状态带下界；mK=0.947对应极限状态带上界。见表6。

表6 闸门主梁混合模型可靠度计算结果

若使用传统的全概率模型进行计算，则mK=0.911 1，σK=0.095 5，求得闸门主梁可靠度指标β=0.724。对比表6中的结果可知，对静水压力统计参数进行区间估计后按概率—区间混合模型计算出的可靠度指标包含了全概率模型计算时的可靠度指标结果。且相较于全概率模型，区间概率混合模型能给出结果在该区间内的置信水平，可信度更高。

5 结 论

本文通过对有限的闸门作用水头数据进行区间分析，可将闸门静水压力统计参数用区间量表示。采用概率－区间混合的可靠度分析方法，以丹江口水库中的深孔闸门为例，对其闸门主梁进行了挠度可靠度分析，主要结论如下。

（1）用区间－概率混合模型计算的结果不仅包含了采用传统全概率模型计算所得的可靠度指标，且能给出可靠度指标在该区间内的置信水平，证明本文所采用的概率－区间混合的可靠度分析方法是合理可行的。

（2）采用区间化参数，能够有效地解决由于样本数据不足而无法得到闸门静水压力精确的概率分布的问题。 □