考虑生态灌溉需求的梯级水电站群多目标优化调度研究

王 娟，王冉旋，王 奕，马志贵，胡新源，钟平安

（1.国家能源集团新疆吉林台水电开发有限公司，新疆伊犁 835700；2.河海大学水文水资源学院，南京 210098）

0 引 言

流域梯级水电站群承担着防洪、生态、灌溉、供水等综合任务，微小的调度方式优化将带来巨大的经济、社会效益提升。实施水电站群联合优化调度不仅可以协调各水电站水量与水头的相互配合，充分挖掘其自身的潜在效益，而且可以利用各级水电站之间的水力、电力联系，实现梯级整体效益最大化［1-4］。

目前，水电站群多目标优化调度研究主要侧重于多目标优化调度数学模型建立、多目标进化算法及其改进、多目标竞争关系分析等方面［5-12］。周研来等针对溪洛渡-向家坝-三峡梯级水库联合蓄水调度过程中防洪、发电、蓄水和航运等目标之间的矛盾，推求了可权衡防洪与兴利之间矛盾的梯级水库联合蓄水方案［13］。杨晓萍等构建了乌江梯级水电站多目标优化调度模型，提出了一种新型的改进多目标布谷鸟算法［14］。现有研究大多侧重于多目标调度数学模型建立和求解算法改进，分析不同决策情景下多目标竞争关系和效益置换机理的成果较少。

本文以流域梯级水电站群为研究对象，综合考虑灌溉、防洪、生态、发电目标建立多目标联合优化调度模型，寻求梯级水电站群多目标联合优化调度方案。采用多目标决策和多情景模拟技术，量化多目标之间的置换率，剖析多目标之间的效益置换机理和水电站群联合优化调度增益机制。

1 流域与电站概况

以我国新疆某流域的梯级水电站为研究对象，该电站群自上而下分别记为：A电站、B电站、C电站、D电站、E电站，拓扑结构如图1 所示。C 站是该区域最大的水电站，承担区域电网主调峰任务。A 电站、B 电站、D 电站为拦河引水式水电站，C 电站和E 电站为坝后式水电站。D 电站与E 电站承担下游灌区的农业灌溉供水任务，D 电站发电引水渠道总长约31 km，发电尾水不用于灌溉，E电站发电尾水直接进入主河道用于农业灌溉。

图1 流域梯级水电站群拓扑结构示意图Fig.1 Topological structure of cascade hydropower stations in the River Basin

2 梯级水电站群联合优化调度模型

该流域梯级水电站群承担农业灌溉用水、生态流量保障、防洪、发电等多目标综合利用任务。本文所构建的模型以梯级水电站群发电效益最大为优化目标，将农业灌溉、生态流量、防洪目标转化为硬性约束条件，采用改进的差分进化算法求解优化调度模型。

2.1 目标函数

模型的调度期为年，时段长取旬，以调度期内梯级水电站群总发电效益最大为目标函数：

式中：NH为水电站总数；i为电站序号；T为总时段数；t为时段序号；prci，t为电站i在时段t的上网电价，元/度；Ni，t为电站i在时段t的出力，kW；dtt为t时段的小时数，h。

2.2 约束条件

（1）水量平衡约束。

式中：Vi，t+1和Vi，t是水电站i在第t时段末、初的水库蓄水量，m3；mi为水电站i的直接上游水库序号；NMi为水电站i的直接上游水库总数；Ii，t、Ri，t、Si，t分别为水电站i在时段t的区间入库流量、总出库流量、损失流量，m3/s；dtt'为第t时段的秒数，s；分别为水电站i在时段t的生态/灌溉供水流量、发电引水流量、弃水流量，m3/s。本文调度模型的时段长为旬，不考虑上下游水库时延。

（2）流量约束。

式中：EGi，tplan为水电站i在时段t的生态、灌溉用水计划值，m3/s；分别为水电站i在时段t的发电流量上下限，m3/s。

（3）水位约束。

（4）出力约束。

（5）水位变幅约束。

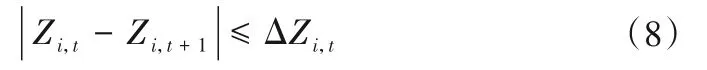
式中：ΔZi，t为水电站i在时段t的水位允许变幅，根据库区水位涨落安全和防冰凌的要求确定，m。

（6）调度期初、期末控制水位约束。

式中：ZIi和ZEi分别为水电站i的起调水位和期末控制水位，m。

2.3 求解算法

差分进化算法（Differential Evolution Algorithm，DE）是基于群体智能理论的启发式搜索算法。差分进化算法在流程框架上类似于遗传算法，主要通过变异、交叉、选择算子实现种群进化，从而最终求解优化问题［15］。本文采用改进的差分进化算法求解联合优化调度模型，主要步骤如下（见图2）：

图2 基本差分进化算法与改进差分进化算法流程对比图Fig.2 Flow chart of the basic DE algorithm and improved DE algorithm

（1）初始种群均匀生成。选择各水库水位为决策变量进行联合编码，算法中每个个体由各水库各时刻的水位组合而成，个体的维度D=NH×（T+1）。初始种群的分布状况对进化算法的全局收敛性能具有较大影响。传统的种群随机生成方式容易导致初始种群代表性不足和求解效率低的问题。本文采用种群均匀生成方式提高初始解的全域分布均匀性：

式中：为第0 代种群第j个个体第d维的决策变量值；Zd和分别为第d维决策变量的搜索上下限；P为种群规模。

（2）适应度函数设计。构造适应度函数ψ(·)来评价个体的优劣程度，该函数在目标函数的基础上额外增加了表征约束条件违反程度项。采用变系数罚函数法处理非等式约束：

式中：λ为最大惩罚系数；g为当前进化代数；Gmax为最大进化代数为水电站i的第k个非等式约束在时段t的违反值；K为非等式约束总数。

（3）变异操作算子。差分进化算法有两种传统的变异模式，分别为DE/Rand/1 和DE/Best/1，前者有利于保持种群多样性，具有较强的全局搜索能力，但收敛速度较慢；后者导向性好、收敛速度快，但容易陷入局部最优解。本文结合两种变异模式的优点，提出“Rand-Best耦合变异模式”用于个体变异：

（4）交叉操作算子。通过交叉操作算子得到试验个体：

（5）选择操作算子。选择操作比较试验个体与父代个体的适应度ψ(·)，适应度函数值较大者进入下一代种群进化过程：

（6）进化终止条件。设置进化终止条件为达到预设的最大进化代数Gmax。

3 结果分析

3.1 计算条件

以该流域某典型年的实际来水过程为例开展梯级水电站群联合优化调度研究。A 电站、B 电站的最小生态流量约束取5.5 m3/s，C电站和E电站汛期水位变幅约束值设为50、1 m/d。D灌区和E灌区的灌溉期为4-10月，生态或农业灌溉用水计划见表1。改进差分进化算法的参数设置为：种群规模P=200、缩放因子F=0.6、交叉概率Pc=0.9、最大进化代数Gmax=5 000。

表1 D灌区和E灌区生态或灌溉用水计划表Tab.1 Ecological or irrigation water plan of irrigation areas D and E

3.2 典型年优化调度结果分析

采用改进的差分进化算法求解梯级水电站群优化调度模型。对于该年份，五库联合优化调度后梯级发电量达40.17 亿kWh，比实际运行发电量（38.51 亿kWh）增加了4.32%，梯级发电效益达10.19亿元，与实际运行效益（9.77亿元）相比增幅为4.30%。

图3（a）展示了C 电站优化与实际水位、发电量过程对比图。与实际调度运行过程相比，C 电站主要通过整体抬高水库水位、增加发电水头来提高发电量，优化的消落水位（1 393.51 m）比实际运行消落水位（1 386.97 m）提高6.54 m。从水位和发电量的年内变化过程看，C 电站发电量增加的月份主要集中在4-8月和11、12月。1-3月，优化调度通过控制发电流量的方式避免水库水位的过度消落，虽然这3 个月的发电量比实际运行少，但优化调度显著提高了4-8月的发电水头，从而提升了后续五个月的发电效益。9-10月，实际调度运行通过增加发电流量的方式提高了发电量，但造成了水库水位的快速回落；而优化调度控制发电流量、保持较高水头运行的方式虽然在一定程度上降低了这两个月的发电量，但显著提高了11-12月的发电效益，实现了年发电效益的最大化和梯级五库整体效益的最优。

图3（b）展示了E 电站优化与实际水位、发电量过程对比图。E 电站优化的水位过程与实际水位过程相比更为平缓，除了1-2月和12月末有轻微波动外，其余时段都维持955 m不变。E 电站增发的月份与C 电站基本一致，主要集中在4-8月和11、12月，这与C电站在这些月份加大下泄流量有关。

图3 优化与实际水位、发电量过程对比图Fig.3 Comparison between the optimized and actual water level and power output process

图4 展示了D 电站和E 电站的生态、灌溉供水流量与发电引水流量过程。D 电站从主河道下泄的生态、灌溉供水流量严格等于两者的用水计划值，其余部分进入发电引水渠用于水力发电。E 电站的出库流量过程也完全满足生态、灌溉用水计划的要求。上述结果表明，本文采用变系数罚函数法能够有效处理流量、出力、水位变幅等非等式约束，所构建的水电站群联合优化调度模型能够在满足生态、灌溉用水计划的前提下实现梯级整体发电效益最优。

图4 生态、灌溉供水流量与发电流量过程Fig.4 Ecological or irrigation water supply and power generation flow

3.3 多目标置换关系定量分析

为了定量分析梯级水电站群发电、生态灌溉用水之间的多目标置换关系，本文引入灌溉用水计划倍比系数（α），通过摄动α值在表1 的基础上对D 灌区和E 灌区的生态灌溉用水计划进行同倍比缩放，生成一系列生态灌溉用水计划情景，计算公式如下：

式中：为水电站i在时段t的生态灌溉用水情景值，m3/s。

利用式（15）生成的生态灌溉用水情景值始终满足最小生态流量（5.5 m3/s）的要求，当α=1 时，即为原始的生态灌溉用水计划。

本算例共摄动10 组α值，采用改进差分进化算法分别求解不同α值情景下的水电站群联合优化调度模型，进而生成非劣解集。图5展示了不同灌溉用水计划倍比系数情景下各电站最优年发电量的结果。图5（a）为发电和灌溉供水目标的非劣解前沿，梯级总发电量和灌溉供水量之间存在明显的竞争关系，随着D 电站和E 电站对下游灌区灌溉供水量的增加，梯级总发电量呈现显著的线性下降趋势。灌溉用水计划倍比系数（α）每增加10%，梯级总发电量将减少0.220 21 亿kWh。将α值换算为灌溉供水量，梯级总发电量和灌溉供水量之间的定量置换率为0.084 5 kWh/m3。需要指出的是本节以典型年实际来水为例，小范围地扰动灌溉供水量，在该实验条件下，发电用水量的变化范围较小，因此计算得到的多目标定量置换率为定值。由图5（b）可知，C 电站发电量随灌溉供水量的增加反而呈增加的趋势。图5（c）表明：D 电站发电量随灌溉供水量的增加呈显著的线性下降趋势，α每增加10%，D 电站年发电量将减少0.244 26亿k Wh，两者的定量置换率为0.093 7 kWh/m3。D 电站为拦河引水式电站，其出库流量优先满足生态、灌溉用水计划并从主河道下泄，剩余部分进入发电引水渠道输送至下游31 km 处的发电厂房，发电尾水无法用于灌溉，因此D 电站的发电和灌溉供水目标之间存在直接竞争关系。由图5（d）可知，E 电站的发电量基本不受灌溉用水计划倍比系数的影响，这是由于E 电站的发电尾水直接进入主河道用于下游灌区农业灌溉，因此发电和灌溉目标不冲突。

图5 不同灌溉用水计划倍比系数情景下各电站最优年发电量变化过程Fig.5 Optimal annual power generation of each hydropower station under different scaling coefficients of irrigation water plan

3.4 多目标效益置换机理分析

为了进一步剖析发电和灌溉目标之间的效益置换机理，重点对C 电站和D 电站的优化调度过程进行详细分析。图6 展示了不同灌溉用水计划倍比系数情景下C 电站优化的水位、发电水头、出库流量、出力过程。灌溉用水计划倍比系数（α）的变化主要影响C电站4-8月的调度方式。4-5月，随着α不断减小，C电站逐渐加大出库流量；6-8月的规律则正好相反，即C 电站的出库流量随着α的减小而逐渐减小。

图6 不同灌溉用水计划倍比系数情景下C电站优化的水位、发电水头、出库流量、出力过程Fig.6 Optimal water level，water head，outflow and power output process of the hydropower station C under different scaling coefficients of irrigation water plan

图7为不同灌溉用水计划倍比系数情景下D 电站优化的生态、灌溉流量和出力过程。由于该典型年汛期来水偏丰，在α=1情景下D 电站6-8月的出力已经达到了装机容量（24 万kW）。当α不断减小时，若维持α=1情景的调度方式，则灌溉用水量的减少部分将全部转化为无效弃水，从而造成D 电站发电效益的损失。因此，随着α不断减小，C 电站和D 电站将联合优化调度方式调整为：4-5月，C电站加大出库流量，D电站提前加大出力直至装机容量；6-8月，C 电站控制出库流量维持D 电站满发且不产生弃水。由图7 可知，D 电站在不同α情景下的生态、灌溉供水流量均严格等于计划值，无弃水产生。图5 也表明，随着α的减小，C 电站发电量减少，D 电站发电量增加，梯级总发电量增加。上述联合优化调度策略的调整在一定程度上牺牲了C电站的发电效益，但通过梯级水电站之间水量、水头的置换实现了梯级整体效益的最大化。

图7 不同灌溉用水计划倍比系数情景下D电站优化的生态、灌溉流量和出力过程Fig.7 Optimal ecological or agricultural irrigation water supply，power output process of the hydropower station D under different scaling coefficients of irrigation water plan

4 结 论

本文构建了考虑生态灌溉需求的梯级水电站群多目标联合优化调度模型，通过多情景模拟定量分析了灌溉、发电目标之间的竞争关系和置换率，剖析了多目标之间的效益置换机理和水电站群联合优化调度增益机制。所建立的模型能够在满足生态、灌溉用水计划的前提下通过整体抬高水库水位、增加发电水头的方式显著提高梯级整体的发电效益。梯级总发电量和灌溉供水量之间存在明显的竞争关系，联合优化调度策略以局部水电站效益损失为代价，通过上下游电站之间水量、水头的置换实现了梯级整体效益的最优。上述结论对于明晰梯级发电效益增益机理、指导梯级水电站群中长期优化调度具有一定的参考价值。 □