基于正交试验的半开式离心泵轴向力影响因素研究

程效锐，骆嘉恒，蒋艺萌

（1.兰州理工大学能源与动力工程学院，兰州 730050；2.甘肃省流体机械及系统重点实验室，兰州 730050）

0 引 言

离心泵轴向力平衡一直是泵行业的热点问题。在叶轮上开设平衡孔是离心泵轴向力平衡的常用方法之一［1，2］。虽然叶顶间隙区域与主流区域相比占比小［3，4］，但间隙处的泄漏流对泵性能的影响不容忽视。叶顶间隙的存在是导致半开式离心泵的扬程效率偏低的主要因素，也是学者们对半开式离心泵研究的热点问题。DONG［5］等分析了4 种不同平衡孔直径轮毂腔内液体的泄露量。结果发现，在不存在平衡孔的情况下，轮毂型腔核心区内液体速度呈轴对称分布。ZHU［6］等提出了在轮毂间隙室增设平衡孔并安装平衡板的“组合孔板压力平衡法”，并证明该方法可以有效降低轴向力。王东伟［7］等提出将平衡孔位置偏移至靠近叶片背面可以改善离心泵的空化性能。CHENG［8］研究了平衡孔比面积大小对离心泵汽蚀性能的影响。刘在伦［10］等通过改变背叶片的宽度和数目来研究其对离心泵轴向力的影响。赵万勇［11］等通过经验公式计算某节段式多级离心泵轴向力，验证了用经验公式计算轴向力的准确性。LIU［12］提出离心泵后密封环间隙与平衡孔面积大小具有最优匹配值。钱晨［13］等通过研究平衡鼓间隙泄漏量变化对叶轮轴向力的影响。刘在伦［14］等通过改变叶轮平衡孔直径和后密封环间隙来改变比面积的方法来研究离心泵轴向力计算方法。XIA［15］指出压力面积不相等产生的轴向推力是预测轴向总推力大小和方向的重要因素。WILL［16］研究发现平衡孔可以减弱叶轮后侧间隙的对流尾迹流动。LIU［17］将径向间隙内的流动简化为平行板模型的黏性层流。

综上所述，许多研究人员最近使用平衡孔或平衡盘来减小轴向力。进行了设计、分析和优化研究。如何降低轴向力在目前的研究中还比较少见。半开式叶轮相比于闭式叶轮来说，没有叶轮前盖板，由于装配原因，会有一定的叶顶间隙来避免摩擦，从而会产生叶顶间隙泄漏。因此，本研究通过考虑叶顶间隙和平衡孔直径变化，以叶顶间隙和平衡孔直径作为试验因素，每个因素取5个水平，对其进行正交方案设计。基于L25（52）正交表，设计了25 组试验方案，对25 组试验方案的数值模拟结果分析以得到最优方案。

1 正交试验方案设计

1.1 模型及参数

本研究的半开式离心泵主要几何参数如表1所示。

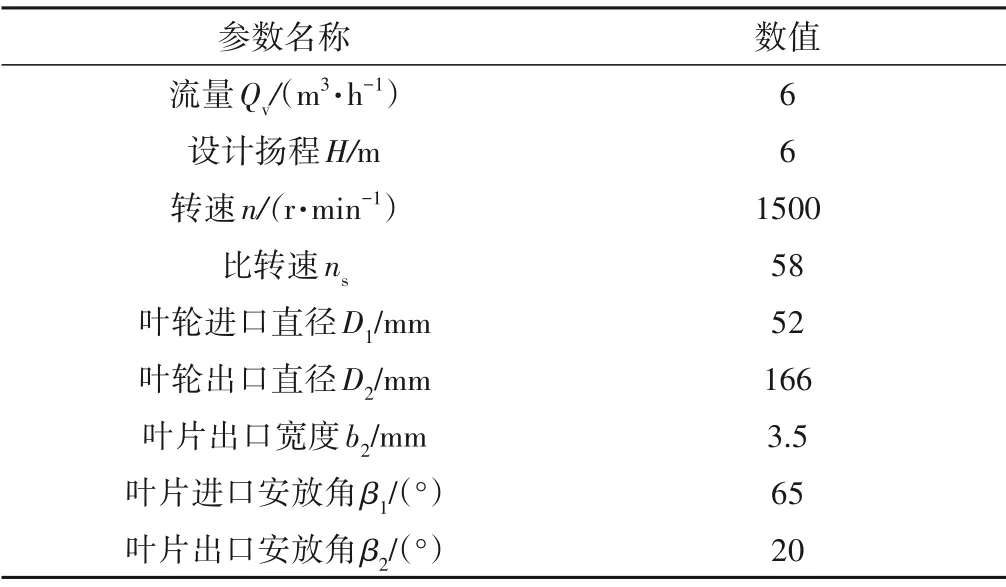
表1 半开式离心泵主要参数Tab.1 Main parameters of semi-open impeller centrifugal pump

本研究主要对半开式离心泵轴向力进行分析，半开式离心泵的轴向力分布如图1所示。半开式离心泵的轴向力是由作用在后盖上的力F1和作用在后盖前侧的力F3、叶顶间隙中的流体施加在叶轮上的力F2、叶片工作面和背面之间的动反力F4组成的矢量和。本研究半开式离心泵的轴向力T1的计算公式如下：

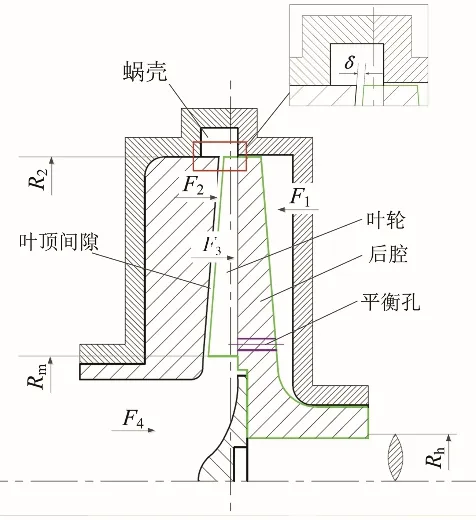
图1 半开式离心泵轴向力示意图Fig.1 Schematic diagram of axial force of semi open centrifugal pump

1.2 试验因素及方案确定

为了降低半开式离心泵轴向力，在本次正交试验方案中，以叶顶间隙和平衡孔直径作为试验影响因素，对影响半开式离心泵轴向力的影响因素进行研究。叶顶间隙是半开式离心泵的重要组成部分，对离心泵性能变化有很大的影响，开设平衡孔是降低离心泵轴向力最有效的方法之一。本研究选取叶顶间隙σ和平衡孔直径d为正交试验的试验因素。试验因素的水平取值如表2所示。

表2 因素水平Tab.2 Factor level

根据正交试验原理和L25（52）标准正交表［17］，由试验因素和因素水平得到25组试验方案，见表3所示。

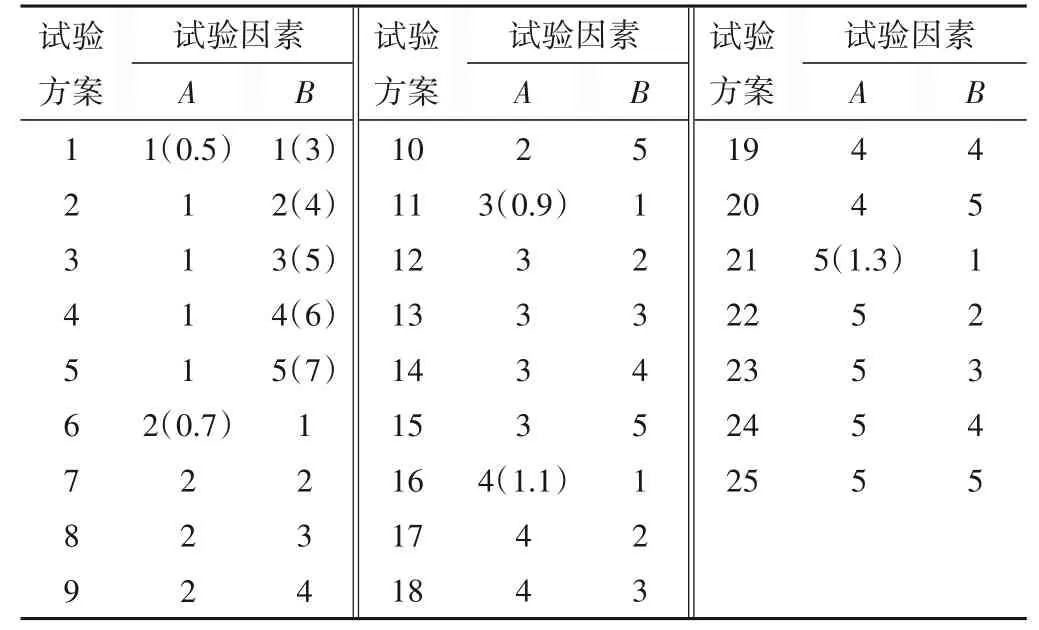
表3 试验方案Tab.3 Test scheme

2 数值计算和试验验证

2.1 三维模型建立

对半开式离心泵的叶轮、叶顶间隙，蜗壳，后腔，进、出口延伸段进行三维建模，整个半开式低比转速离心泵的三维模型如图2所示。半开式离心泵整体水体图如图2（a）所示，叶顶间隙、后腔水体示意图如图2（b）所示。

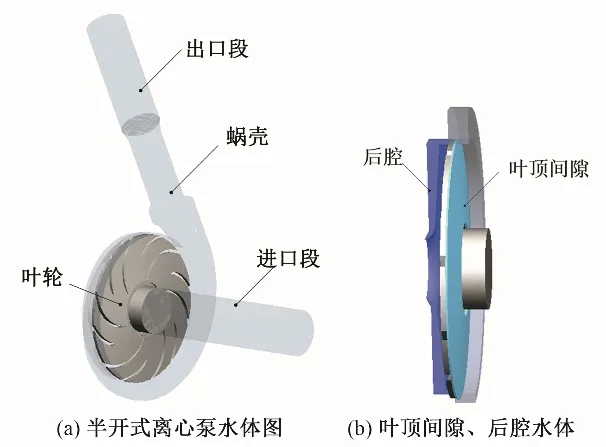
图2 半开式离心泵水体图Fig.2 Water body diagram of semi open impeller centrifugal pump

2.2 计算域网格划分

半开式离心泵流体域主要由进口延伸段，叶顶间隙，叶轮，蜗壳，后腔和出口延伸段六部分组成。应用ICEM 软件对进口延伸段，蜗壳，后腔和出口延伸段流体域采用四面体非结构化网格进行划分，对叶顶间隙和叶轮采用六面体结构化网格划分，对蜗壳和叶轮进行了局部加密处理，对叶顶间隙区域的网格进行了局部加密，加密层数为20 层，叶顶间隙近壁面第一层网格高度为6×10-5m，y+值取1～10，满足SST湍流模型计算的需要。主要流体域网格如图3所示。

图3 计算域网格示意图Fig.3 Schematic diagram of computational domain grid

考虑到网格数量和质量对计算结果的影响。在保证网格质量的情况下，分别采用网格数为540 万个、600 万个、680 万个和860 万个进行网格无关性验证。对比4 组不同网格数的半开式离心泵在0.8QV、1.0QV和1.2QV三种工况下的总轴向力变化情况，如图4 所示。从图4 中可以看出，当网格数增加时，低比转速离心泵总轴向力总体为下降趋势。当网格数达到680 万个时，3 种工况下的扬程趋于平稳。在设计流量下，从680～860 万个，总轴向力最大变化为24.83 N，占最高轴向力的3%，可认为是计算误差。因此，采用680万个网格数为计算域网格数。

图4 网格无关性验证图Fig.4 Grid independence verification diagram

2.3 数值方法和边界条件

本研究对半开式离心泵进行全流道数值模拟。采用SSTk-ω湍流模型，该模型对具有逆压梯度或者流动分离的流场中有较好表现。SSTk-ω模型的基本形式如下：

式中：Pk表示湍流脉动动能k的生成项；Pω为湍流脉动频率的生成项；Γk和Γω分别代表k与ω的有效扩散系数；Yk和Yω分别代表k与ω的耗散项；Dω代表正交扩散项。

假定离心泵在稳定工作时，内部流场为定常流动，选择SSTk-ω湍流模型。假设固体壁面无滑移，近壁面采用标准壁面函数。压力与速度的耦合计算采用SIMPLE 算法，对方程组的离散格式，压力项采用标准格式，速度项、湍动能项和湍流脉动频率均采用一阶迎风格式。

离心泵叶轮旋转区域与蜗壳、吸水室静止区域之间的耦合模型，选用多参考旋转坐标系模型（Multiple Reference Frame），旋转速度为离心泵转速（1 500 r/min），进口边界条件采用速度进口（Velocity-inlet），出口边界条件采用自由出流（Outflow），各交界面设为Interface，收敛精度为10-5。

2.4 数值模拟有效性验证

该试验在兰州理工大学流体机械及工程重点试验室进行，测试系统为低比转速离心泵可视化试验台，试验系统图如图6所示。试验中记录了流量从0 到9 m3/h 的泵进、出口压力和流速，通过公式计算出相应的泵的扬程和效率。离心泵的扬程计算公式见式（4），效率计算公式见式（5）：

图6 试验系统图Fig.6 Test system diagram

式中：H为扬程，m；Z为位置水头，m；P为压力，Pa；v为流速，m/s；ρ为流体密度，kg/m3；下标1表示泵进口，下标2表示泵出口。

式中：Q为流量，m3/s；H为扬程，m；P为输入功率，kW；ρ为流体密度，kg/m3。

试验设置转速为1 500 r/min，数值模拟流量从4 m3/h 到8 m3/h。如图5 所示，在额定工况下，数值模拟扬程值与试验值变化率在5%以内，数值模拟效率值和模拟值变化率在5%以内。这是由于本次研究对象为低比转速离心泵，而且流量较小，因此会出现较小的数值误差。

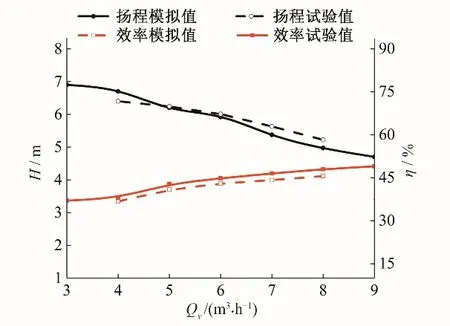
图5 离心泵的试验曲线与数值计算曲线Fig.5 Test curve and numerical calculation curve of centrifugal pump

2.5 叶轮和隔舌相对位置对泵轴向力及性能影响

对本研究离心泵叶轮叶片出口和隔舌位置进行调整，以长叶片出口与隔舌对齐为相对角度0°，压水室顺时针旋转以改变相对角度，设计了0°、15°、30°、45°四种位置方案。数值计算结果如图7所示，泵轴向力随着相对角度的增大逐渐减小，相对位置为0°时轴向力956.59 N，相对位置为45°时轴向力为896.795 N，降低了59.795 N，占原始方案泵轴向力的6%，扬程随相对位置变化在5%以内，效率随相对位置变化在1%以内。因此叶轮与隔舌相对位置对本研究泵轴向力及性能影响不大。鉴于以上结论，在本研究中采用复合叶轮长叶片出口正对蜗壳隔舌位置来继续本研究，具体的相对位置见图8所示。

图7 叶轮和隔舌相对位置对泵轴向力及性能影响曲线Fig.7 The influence curve of the relative position of the impeller and the diaphragm on the axial force and performance of the pump

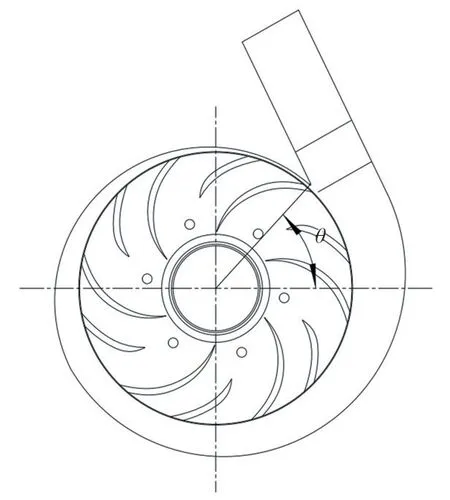
图8 叶轮叶片出口和蜗壳隔舌位置Fig.8 The position of the impeller blade outlet and the volute separation tongue

3 正交试验结果分析

对表3 中的25 组正交试验方案在额定工况下进行数值模拟。以本研究离心泵扬程、效率和输入功率作为试验指标得到如表4 所示的正交试验结果一，以半开式离心泵轴向力的组成部分作为试验指标得到如表5所示的正交试验结果二。

3.1 直观分析

根据表4 正交试验结果一所示。当叶顶间隙一定时，随着平衡孔直径的增大，该低比转速离心泵的扬程和效率都逐渐降低，输入轴功率逐渐增加。根据表5正交试验结果二所示，当叶顶间隙一定时，随着平衡孔直径的增大，该泵的轴向力逐渐降低，主要表现为作用在后盖板上的力F1的降低。说明增大平衡孔直径可以有效的降低轴向力。在相同的平衡孔直径下，随着叶顶间隙的增加，该泵轴向力也呈下降趋势，这说明叶顶间隙的增大也可以平衡轴向力。综上所述，叶顶间隙和平衡孔直径增大会降低轴向力。

表4 正交试验结果一Tab.4 Results of orthogonal test 1

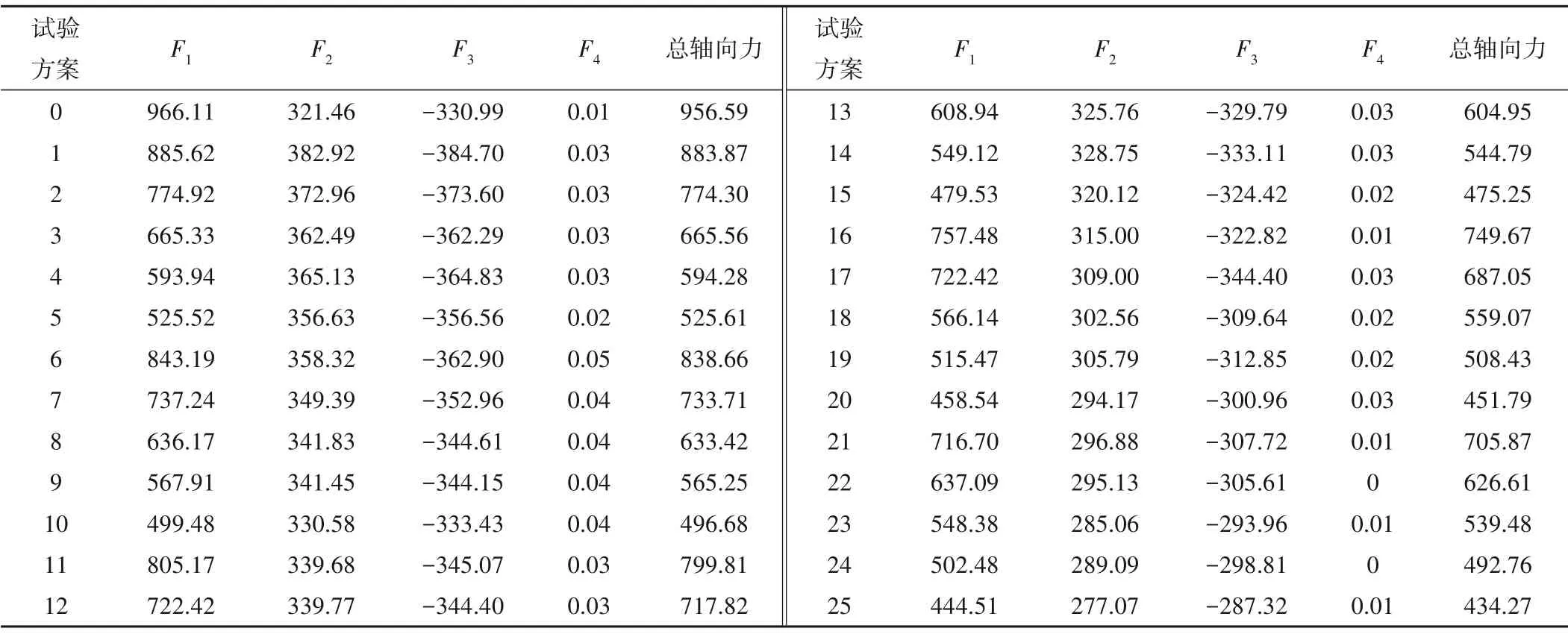
表5 正交试验结果二 NTab.5 Results of orthogonal test 2

3.2 极差分析

极差分析是处理正交试验数据的常用方法，极差值R的大小能够直接表明试验因素对试验评判对象的影响程度［18，19］。极差越大，说明该因素下的因素对试验指标的影响越大。根据表6中的计算数据，得出因素水平对4个试验评判对象的影响。

表6 试验结果极差分析Tab.6 Range analysis of test results

通过极差分析以看出，A（叶顶间隙）、B（平衡孔直径）两个因素对扬程、效率和轴向力影响程度不同，对输入功率变化影响不大。为直观显示试验因素对评判对象影响程度的影响，以试验因素为横坐标，评判对象（扬程、效率和轴向力）为纵坐标，得到如图9～11所示的水平指标关系。

如图9 所示，在额定流量下，A因素（叶顶间隙）变化对扬程的影响较大，随着叶顶间隙的增大，扬程下降的幅度较大。叶顶间隙从0.5 mm 增加到1.3 mm，离心泵扬程从7.12 m 降低到6.18 m，降低了9%。这是由于叶顶间隙增大引起的叶顶间隙泄漏量也随之增大，从而引起的扬程下降。而B因素（平衡孔直径）变化对于扬程的影响较小，平衡孔直径由3 mm 增加到7 mm，离心泵扬程从6.72 m 降低到6.49 m，降低了3%，这也说明了平衡孔直径在一定范围内变化，基本不会影响到半开式离心泵的扬程。

图9 各因素水平与扬程指标关系Fig.9 Relationship between each factor level and head index

如图10所示，在设计流量工况下，叶顶间隙的增大和平衡孔直径的增大，都会引起效率的下降。叶顶间隙从0.5 mm 增加到1.3 mm，离心泵效率从41.74%降低到38.17%，降低了3%。这而B 因素（平衡孔直径）变化对于扬程的影响较小，平衡孔直径由3 mm 增加到7 mm，离心泵扬程从42.63%降低到38.23%，降低了3.8%，这是因为叶顶间隙增大和平衡孔直径增大都会引起流体泄漏量的增加，从而导致叶轮效率降低，进一步影响该低比转速离心泵的效率。

图10 各因素水平与效率指标关系Fig.10 Relationship between the level of each factor and efficiency index

如图11 所示，叶顶间隙从0.5 mm 增大到1.3 mm，轴向力从688.72 N 降低到559.8 N，降低了128.92 N。而平衡孔直径由3 mm 增加到7 mm，轴向力从795.58 N 降低到476.72 N，轴向力降低了318.86 N，占到原始方案轴向力的34%。这充分说明叶顶间隙的增加对降低该泵的轴向力有一定的影响，而平衡孔的增大对半开式离心泵降低轴向力有显著作用。增大平衡孔直径可以有效地降低半开始叶轮低比转速离心泵的轴向力。

图11 各因素水平与轴向力指标关系Fig.11 Relationship between the level of each factor and axial force index

通过以上极差分析，可以得到的较优的试验方案分别为：对于扬程的优化水平组合为A1B1，对于效率的优化水平组合为A1B1，对轴向力的优化水平组合为A5B5。

3.3 最优方案的确定

综合以上分析，得到本研究正交试验的最优方案为A1B5，即叶顶间隙σ= 0.5 mm，平衡孔直径为d= 7 mm。

4 数值计算结果分析

4.1 数值计算曲线对比

原模型和最优方案半开式离心泵性能对比曲线如图12 所示。最优方案和原始方案的扬程在各个工况下基本保持一致，而效率在小工况流量下区别较大，随着流量的逐渐增加，效率变化逐渐减小。这是因为与原模型相比，叶顶间隙从1.3 mm降低到0.5 mm，叶顶间隙泄漏量减小，而开设平衡孔会造成一定的泄漏量，根据表5正交试验结果二来看，扬程变化不大。叶顶间隙降低，流体泄漏量减小，由于开设7 mm 平衡孔，流体流经后盖板时会产生较小的泄漏量，导致泵效率有所降低。优化前后的轴向力随流量增加变化较小，但总的来说，轴向力降低的比较明显，达到了降低轴向力的目的。在额定工况下，扬程降低了0.3%，效率降低了3.67%，轴向力降低了45%。由此可以证明在额定工况下，最优方案可以显著降低该低比转速离心泵的轴向力，同时对扬程和效率的影响较小。

图12 原始方案和优化方案曲线对比Fig.12 Comparison of curves between riginal scheme and optimized scheme

4.2 轴向力变化分析

根据正交试验结果，对原模型和正交试验结果进行各个组成部分的轴向力对比，如图13 所示。由图13 中可以看出，原模型轴向力主要来源于作用在后盖板上的力F1，这是因为半开式离心泵没有前盖板，因此轴向力主要分布在后盖板上。

图13 原模型和优化方案轴向力组成对比Fig.13 Comparison of axial force composition between original model and optimized scheme

原模型和最优方案作用在叶轮后盖板前侧的力F3和叶尖间隙中的流体施加在叶轮上的力F2均变化不大，其中原模型的F3比最优方案高25 N，原模型的F2比最优方案小24 N，占原始方案总轴向力的2.6%，对轴向力的影响可以忽略不计。叶片工作面和背面之间的动反力F4几乎没有变化，原模型该项为0.01 N，最优方案为0.03 N，可以忽略不计。作用在后盖上的力F1变化十分明显，最优方案的轴向力与原模型降低了440.59 N，占原模型轴向力的45.6%。这是因为叶顶间隙减小，叶顶间隙泄漏量减小，流体通过平衡孔的泄露量较大，从而导致后腔内侧的压力增加，进一步降低了该半开式离心泵的轴向力。

4.3 半开式离心泵轴面压力和速度分析

图14（a）为额定工况下原模型和最优方案半开式离心泵轴面压力云图，从图中可以看出，原始方案与优化方案的压力分布明显不同。最优方案叶顶间隙和叶轮的压力基本不变，而后腔压力降低十分明显，说明作用在后盖板上的力F1的变化是轴向力降低的主要组成部分。从图14（b）可以看出，该面上的速度增加，也反映出它的压力降低，进一步验证了最优方案可以有效的降低轴向力。

图14 额定工况下原模型与最优模型轴面压力与轴面速度场分布Fig.14 Distribution of axial pressure and axial velocity field of original model and optimal model under rated condition

4.4 半开式离心泵湍动能分析

图15 为额定工况下原模型和最优方案半开式离心泵轴面湍动能分布图，可以看出，最优方案的湍动能向后腔转移，主要体现在后腔与蜗壳的交接处和平衡孔向后腔传递，叶顶间隙和叶轮的湍动能发生断裂和减小，说明最优方案对于叶顶间隙和叶轮的能量损失减小。最优方案叶轮和蜗壳交接处明显减小，说明动静耦合面的湍动能减小，能量损失减小。分析表明，最优方案对半开式离心泵减小能量损失有一定的作用。

图15 额定工况下原模型与最优模型轴面湍动能分布Fig.15 Axial turbulent kinetic energy distribution of original model and optimal model under rated conditions

5 结 论

本研究采用数值分析和试验相结合的方法对半开式离心泵轴向力的影响因素进行正交试验分析研究，通过对比分析不同影响因素对该半开式离心泵轴向力分布规律，得出以下结论。

（1）当叶顶间隙一定时，增大平衡孔直径对降低轴向力有显著作用，平衡孔直径由3 mm 增加到7 mm，轴向力由792.58 N降低到476.72 N，降低了315.86 N，占原模型总轴向力的33%；当平衡孔直径一定，增大叶顶间隙也会降低轴向力，叶顶间隙由0.5 mm 增加到1.3 mm，轴向力由688.72 N 降低到559.80 N，降低了128.92 N，占原模型总轴向力的13%。

（2）通过对正交试验结果进行极差分析，以降低轴向力为主要评判目标，得到叶顶间隙与平衡孔直径最优匹配方案为叶顶间隙σ=0.5 mm，平衡孔直径为d=7 mm。

（3）根据正交试验结果发现，半开式离心泵的轴向力降低主要是由于作用在后盖上的力F1的降低导致的。最优方案的轴向力与原模型相比降低了440.59 N，占原模型总轴向力的45.6%。 □