基于GA-BP神经网络与正态区间估计的需水预测——以邯郸市为例

马于航，索梅芹

（1.河北工程大学水利水电学院，河北邯郸 056021；2.河北工程大学河北省智慧水利重点实验室，河北邯郸 056038）

0 引 言

城市需水预测是城市水资源管理和规划的重要环节，也是供水系统优化运行的基本内容［1］。城市需水量是一个受人口、地域、经济发展等诸多因素影响的变量，具有较强的非线性和不确定性。现有的需水预测方法包括传统预测（回归分析、指数平滑、趋势外推法等）［2-5］和新型预测（BP 神经网络、灰色预测、混沌理论、组合模型等）［6-12］。马兴冠等［13］研究表明指数预测、定额预测法、趋势法等方法只能反映一种平稳的几何增长过程，预测精度偏低，聂红梅［14］等比较了主成分回归、逐步回归、灰色模型和BP神经网络四种城市需水预测模型，其中BP神经网络具有强大的非线性拟合能力，利用BP 神经网络进行需水预测具有较高的预测精度；但在实际使用过程中，BP 神经网络具有收敛速度慢、易陷入局部最优的缺点。为加强BP 神经网络全局搜索的能力、提高网络性能与预测精度，引入遗传算法优化BP神经网络，构建GA-BP神经网络预测模型，具有一定的计算效果。在实际用水过程中，由于不确定因素的影响，需水量具有波动性和不确定性的特点，单一使用GA-BP神经网络预测模型得到的点预测结果、难以解决需水量的波动性和不确定性，而利用区间预测可以更好地反映城市需水量的实际情况。因此，在GA-BP 神经网络的基础上，引入正态区间估计的方法，进行城市需水量区间预测，可得到更稳定、更准确、更接近实际的预测效果。

本文以邯郸市为例，构建基于GA-BP神经网络与正态区间估计的组合预测模型，该模型使用主成分分析法、灰色关联分析法对需水影响因子进行两次筛选，筛选后的需水影响因子作为输入GA-BP 神经网络的训练样本，在使用GA-BP 神经网络预测基础上，引入正态区间估计，以实现提升预测精度、更好地反映城市需水量实际情况的目的。

1 组合预测模型的建立

基于GA-BP 神经网络与正态区间估计的组合预测模型主要分为以下几部分：主成分分析、灰色关联分析、GA-BP 神经网络预测、正态检验、正态区间估计。设计的组合模型技术路线如图1所示。

图1 组合模型设计Fig.1 Combined model design

1.1 影响因子筛选

1.1.1 主成分分析法

主成分分析法是一种常用的数据分析方法，其基本思想是将多指标的数据通过数据的线性变化（基变换）转换为几个线性无关的综合指标，舍弃部分信息量，从而达到数据降维和解决数据间多重共线性的目的。基本原理：

设Xmn=（X1，X2，…，Xm）为m个标准化指标组成的数据矩阵，每个指标有n个样本；

对矩阵X进行线性变化（基变换）得Ykn=PkmXmn，YT=（y1，y2，…，yk）（k＜m）为降维后的数据矩阵，由k个指标组成，每个指标有n个样本，这是降维的基本形式；

主成分分析法要求降维后数据矩阵的协方差矩阵为对角矩阵，即降维后各指标间线性无关且每次提取的主成分信息量最大：

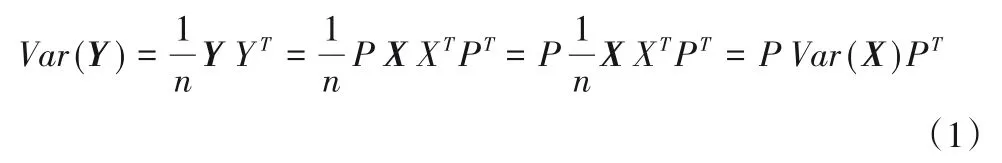
不难看出，进行线性变换时连续提取主成分的过程，其实就是矩阵X的协方差矩阵的对角化过程。通过矩阵对角化的方式对矩阵X的协方差矩阵进行运算，所计算得到的最大的特征值即为第一主成分的方差，也代表了信息量的多少，而相应的特征向量即是通过矩阵X线性变换所得到第一主成分的特征系数，它也可视为相应指标在主成分中所占有的最大权重。

1.1.2 灰色关联分析法

灰色关联分析法是一种关于多指标数据的分析方法，能够定量分析不同指标数据对某个指标的影响程度。基本计算过程包括：

设指标X0（k）=［X0（1），X0（2），…，X0（m）］；

影响因素指标Xi（k）=［Xi（1），Xi（2），…，Xi（n）］，i=1，2，…，n；

消除量纲影响进行初值化处理：

计算指标与影响因素数据Xi（k）差的绝对值：

计算关联系数：

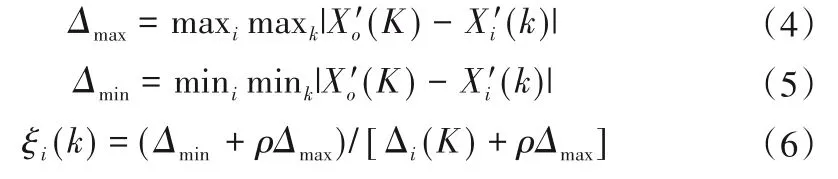
计算各影响因素与指标的关联度，并根据得到的关联度由大到小排序。关联度越大，代表两者之间的相关性就越强：

1.2 神经网络预测

1.2.1 BP神经网络

BP（Back Propagation）神经网络是一个由误差反向传播算法训练的多层前馈网络，大量研究证实了BP 神经网络在时间序列预测中的优越性，其基本结构由输入层、隐藏层和输出层三部分组成。其核心思想是模拟脑神经信号的传播方式，使用样本值进行多次训练，采用梯度下降的方法，进行误差反向传播，调整权值、阈值，确定影响因素与输出值之间的映射关系。其基本原理如图2所示。

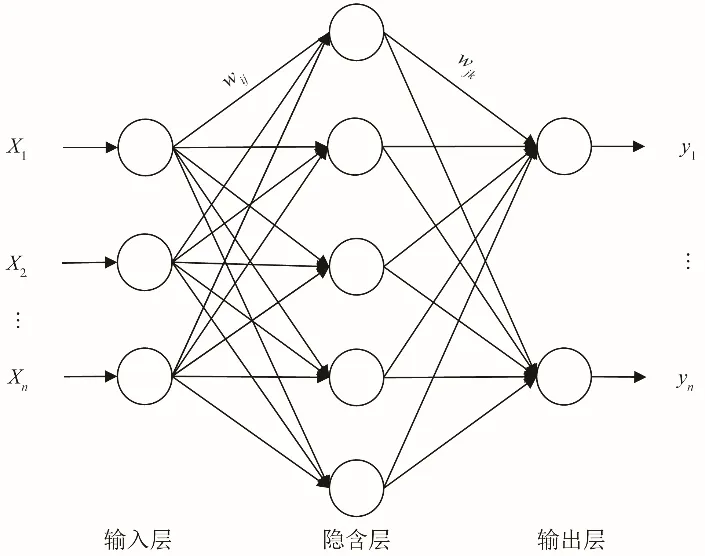
图2 BP神经网络基本结构Fig.2 Basic structure of BP neural network

神经元节点间正向传播，设输入层神经元Xi，隐含层神经元Hj，信号激活函数f（x），权重ωij，阈值bj：

误差反向传播调整权重，实际值Yn，模拟值yn，E（ω，b）为变量ω，b的误差函数：

1.2.2 GA-BP神经网络

GA-BP（Genetic Algorithm-Back Propagation）神经网络是使用遗传算法优化的BP神经网络。随机生成多组BP神经网络的权值、阈值（群体），个体是其中的一组权值、阈值，每个个体的染色体为权值或阈值，每条染色体的基因为权值或阈值的二进制编码，使用误差均方差或平均相对误差作为适应度函数，较小的误差个体更容易被选择（轮盘赌选择），从而进行染色体交叉以及基因变异，最终选出最优个体，即优异的影响因子与输出值间的映射关系。

1.3 正态区间估计

1.3.1K-s正态检验

K-s正态检验是一种用于测试单个样本是否符合特定分布的方法。基本原理是将样本数据的累积频率分布与正态分布进行比较。如果两者之间的差异很小，则假定该数据样本符合正态分布标准。在SPSS 软件上对样本进行K-s检验，计算P值，若P＞0.5，则接受零假设，认为样本符合正态分布。

1.3.2 正态区间估计

若总体X服从正态分布N（μ，σ2），σ2未知，对μ做区间估计。假设X1，X2，…，Xn是总体X的一个样本，样本均值为-X，样本方差为S2，则：

在置信度为1-α下，μ的置信区间为：

2 组合预测模型的应用与分析

2.1 需水量影响因子的率定

需水量的变化是社会、经济、科技、文化等因素综合作用的结果。本文结合邯郸市的用水结构，选取《邯郸市水资源公报》和《邯郸市统计年鉴》中2004-2019年的数据，初步选取了25 个影响邯郸市需水的因素：农业用水量（X1，亿m3）、工业用水量（X2，亿m3）、生活用水量（X3，亿m3）、地区生产总值（X4，亿元）、第一产业生产总值（X5，亿元）、第二产业生产总值（X6，亿元）、第三产业生产总值（X7，亿元）、农林牧渔业总产值（X8，万元）、粮食总播种面积（X9，hm2）、粮食总产量（X10，t）、有效灌溉面积（X11，hm2）、温度（X12，℃）、降水量（X13，mm）、日照时长（X14，h）、工业总产值（X15，万元）、重轻工业比值（X16）、发电量（X17，亿kWh）、洗煤（X18，万t）、钢材（X19，万t）、常住人口（X20，万）、城镇化率（X21）、年平均居民可支配收入（X22，元）、年平均居民消费性支出（X23，元）、年平均每人地区生产总值（X24，元）、公园绿地面积（X25，hm2）。

总需水量影响因子指标筛选。因为主成分分析法分析需水影响因子的主要目的是筛除存在重复信息的数据指标，灰色关联分析法主要目的为筛选出与目的指标发展趋势相近的数据指标，所以为保证入选指标具有代表性、全面性且对预测结果有促进作用，使用主成分分析法和灰色关联法对指标进行两次筛选。具体步骤和方法如下：

（1）使用主成分分析法对25个影响因子指标进行分析。分析结果如表1所示。

表1 相关系数矩阵特征值及方差贡献率Tab.1 Eigenvalues and variance contribution of correlation coefficient matrix

从表1得，4个主成分累计方差贡献率已达91.245%，说明4个主成分基本包含了全部指标蕴含的信息，因此提取4 个主成分，4 个主成分包含方差贡献率分别为69.61%、9.35%、7.32%、4.96%，据此对4个主成分中指标提取个数依次为14、2、2、1。

（2）将主成分中指标的特征向量由大到小排列，根据提取个数依次提取指标。结果如表2所示。

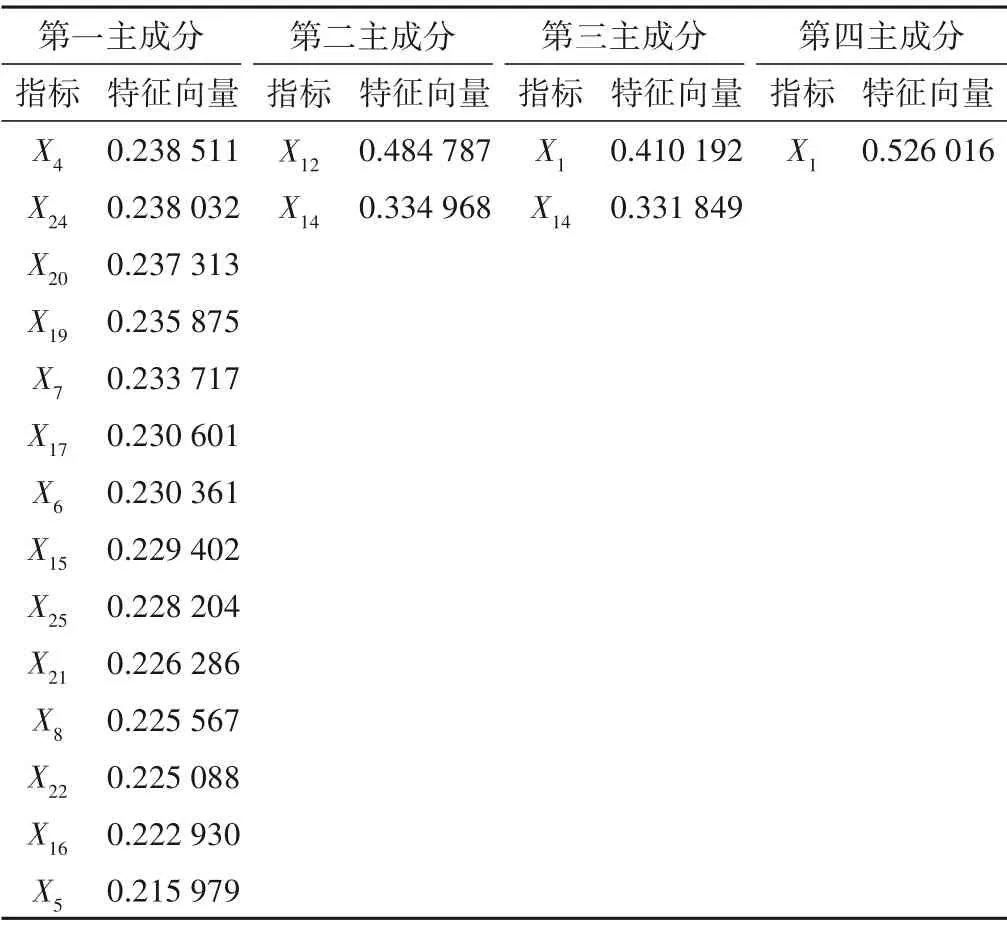
表2 主成分中指标的提取Tab.2 Extraction of indicators in principal components

提取主成分时，对应的特征向量是从数据矩阵线性变换获得的主成分系数，也可以视为主成分中指标的权重。因此，将主成分中所含指标的特征向量由大到小进行排列，按照贡献率的大小依次提取前14、2、2、1个指标。提取指标为X1、X4、X5、X6、X7、X8、X12、X14、X15、X16、X17、X19、X20、X21、X22、X24、X25，总 计17 个指标。

（3）计算所有需水因子指标与总需水量的灰色关联系数，使用灰色关联系数对主成分分析提取的指标第二次筛选。计算结果如表3所示。

表3 灰色关联系数计算结果Tab.3 Calculation results of gray correlation coefficients

结合主成分分析法提取的指标，依据灰色关联系数最终筛选出10 个总需水影响因子指标：第一产业生产总值、第二产业生产总值、有效灌溉面积、温度、日照时长、工业总产值、发电量、常住人口、城镇化率、地区生产总值（X5、X6、X11、X12、X14、X15、X17、X20、X21、X24）。

农业用水影响因子：第一产业生产总值、农林牧渔业总产值、粮食总播种面积、粮食总产量、有效灌溉面积、温度、降水量、日照时长8 个影响因子；工业用水影响因子：第二产业生产总值、发电量、工业总产值、洗煤、重轻工业比值、钢材6 个影响因子；生活用水影响因子：地区生产总值、常住人口、城镇化率、居民可支配收入、居民消费性支出、人均地区生产总值6个影响因子；总需水量影响因子：第一产业生产总值、温度、日照时长、有效灌溉面积、第二产业生产总值、发电量、工业总产值、常住人口、人均地区生产总值、城镇化率10个影响因子。

2.2 BP 神经网络及GA-BP 神经网络需水预测结果与分析

根据上述选定的用水影响因素，在matlab上编写BP神经网络、GA-BP 神经网络代码，使用2004-2016年的需水量和需水影响因素数据作为神经网络的训练样本，利用BP 神经网络、GA-BP 神经网络分别进行模拟，使用相对误差指数作为检验指标，对2017-2019年的数据样本进行检验分析。模拟预测结果如图3所示，模拟预测结果统计如表4所示。

表4 BP神经网络和GA-BP神经网络模拟预测结果统计 %Tab.4 Statistics of simulation prediction results of BP neural network and GA-BP neural network

图3 BP神经网络和GA-BP神经网络模拟预测结果Fig.3 BP neural network and GA-BP neural network simulation prediction results

为检验GA-BP神经网络预测精度，使用训练样本平均相对误差、检验样本最大相对误差两个指标从历史用水数据拟合、未来用水预测两个方面与BP 神经网络进行对比，其中，在对邯郸市农业用水、工业用水、生活用水、总用水进行模拟预测时，BP 神经网络训练样本平均相对误差为1.22%、2.00%、1.69%、1.24%，检验样本最大相对误差为2.37%、4.76%、4.12%、4.69%；GA-BP 神经网络训练样本平均相对误差为1.79%、0.78%、1.62%、0.85%，检验样本最大相对误差为1.85%、2.38%、1.87%、2.84%。可见，BP神经网络与GA-BP 神经网络训练样本平均相对误差基本都小于2%，训练样本平均相对误差较小，检验样本最大相对误差都在5%以下，整体上均可满足需水预测要求；对比BP 神经网络和GA-BP 神经网络预测结果，GA-BP 神经网络的历史用水数据拟合更好、预测精度更高。

2.3 基于GA-BP 神经网络与正态区间估计的组合需水预测

单一使用GA-BP神经网络进行需水预测，预测结果并不能很好的反映未来需水量实际状况，其主要原因为：一方面使用GA-BP 神经网络得到的预测结果为点预测结果，不能反映未来需水量的波动性和不确定性特点，另一方面，在实际进行GABP 神经网络预测操作时，即使在相同参数条件下，也会出现由于初始权重、随机阈值、过拟合等随机因素造成预测结果不唯一的现象。因此，构建基于GA-BP神经网络与正态区间估计的组合需水预测模型，在使用GA-BP 神经网络预测的基础上，引入正态区间估计，使用GA-BP神经网络的点预测结果作为正态区间估计样本，进行区间预测，具体步骤如下。

（1）将邯郸市2004-2016年总需水量与影响因子数据作为训练样本，2017、2018年数据作为检验样本，使用GA-BP 神经网络进行多次拟合，并选择训练结果，挑选出训练样本平均相对误差小于2%以及检验样本最大相对误差小于2%的GA-BP神经网络，然后使用挑选出的GA-BP 神经网络对2019年总需水量进行预测，取80 个GA-BP 神经网络点预测结果。预测结果频率分布如图4所示，预测结果统计如表5所示。

表5 GA-BP神经网络2019年总需水量点预测结果描述统计Tab.5 GA-BP neural network 2019 total water demand point forecast results descriptive statistics

图4 GA-BP神经网络2019年总需水量点预测结果频率分布Fig.4 Frequency distribution of GA-BP neural network 2019 total water demand point forecast results

（2）在SPSS 软件上对80 个GA-BP 神经网络2019年总需水量点预测结果样本进行K-s检验，经计算P=0.2，P＞0.05，接受零假设，即80 个2019年总需水量点预测结果样本服从正态分布。根据正态分布均值区间估计得：在置信度95%的情况下，基于GA-BP 神经网络与正态区间估计的邯郸市2019年总需水量区间预测结果为19.083 4～19.279 2 亿m3。邯郸市2019年总需水量为19.278 4 亿m3。结果分析如表6所示。

表6 基于GA-BP神经网络与正态区间估计的2019年总需水量区间预测结果Tab.6 Total water demand interval forecast results for 2019 based on GA-BP neural network with normal interval estimation

从表5 可以看出，在平均相对误差小于2%、检验样本最大相对误差小于2%的条件下，使用单一GA-BP 神经网络预测模型对2019年总需水量预测，点预测结果预测相对误差在-6.2%～5.13%之间。从表6 可以看出，在GA-BP 神经网络预测基础上引入正态区间估计的组合模型对2019年总需水量预测，预测相对误差在-1.01%～0.004%之间，基于正态区间估计与GA-BP神经网络的组合需水预测模型更稳定、预测精度更高。

3 结论与建议

3.1 结 论

本文结合邯郸市用水结构，采用主成分分析法、灰色关联分析法对邯郸市需水因素数据进行两次筛选，在使用GA-BP神经网络得到邯郸市需水量点预测结果的基础上，引入正态区间估计，对邯郸市总需水量进行区间预测。主要结论如下。

（1）BP 神经网络与GA-BP 神经网络两种预测方法均可满足基本需水预测要求，且GA-BP神经网络的历史用水数据拟合更好、预测精度更高；其中，在对邯郸市农业用水、工业用水、生活用水、总用水进行模拟预测时，GA-BP 神经网络训练样本平均相对误差为1.79%、0.78%、1.62%、0.85%，检验样本最大相对误差为1.85%、2.38%、1.87%、2.84%。

（2）单一使用GA-BP 神经网络对未来需水量进行预测时，预测结果不稳定，会出现误差较大的现象，其中，在训练样本平均相对误差小于2%、检验样本最大相对误差小于2%的条件下，使用单一GA-BP 神经网络预测模型对2019年总需水量预测，预测相对误差在-6.2%～5.13%之间。

（3）与单一使用GA-BP 神经网络预测模型相比，基于GABP神经网络与正态区间估计的组合需水预测模型更稳定、预测精度更高、更能反映未来需水量实际状况。在置信度95%的情况下，基于GA-BP 神经网络与正态区间估计的邯郸市2019年区间预测相对误差在-1.01%～0.004%之间。

3.2 建 议

城市需水预测从时间尺度上可分为短期预测（一年以内）、中期预测（一至十年）、长期预测（十年以上）。本文构建了基于GA-BP 神经网络与正态区间估计的组合预测模型，限于数据资料，以邯郸市为例仅验证了中期预测的可靠性，对于预测时间尺度在十年以上的长期预测来说，训练样本数据代表性较差，不能反映如未来节水政策、未来城市建设等不可量化信息，在预测精度上会有折扣；对于中、短期预测来说，节水政策、城市建设等不可量化指标信息在历史用水数据趋势中有所体现。因此从理论上讲，该模型在中、短期预测上有不错的精度，但在实际应用过程中需要进一步验证。 □