考虑再生水的多种组合情景需水预测及供需平衡分析

刘 晶，许月萍，郭玉雪，王贺龙，郑超昊，吴 垚

（1.浙江大学建筑工程学院水文与水资源工程研究所，杭州 310058；2.浙江省水利河口研究院，杭州 310058）

0 引 言

水资源短缺问题已成为中国城市转型发展面临的最大“硬件”约束之一［1］。因此，为保障社会经济可持续发展，需对水资源进行合理规划与配置。需水预测是水资源配置的前提，科学准确的需水预测结果为水资源供需平衡分析奠定基础。20 世纪70年代以来，国内外陆续开展了中长期需水量预测的工作。预测方法主要包括指数预测法、定额法、趋势预测法、回归分析等传统方法［2-6］和粒子群算法、人工神经网络、灰色模型理论、小波分析、随机森林模型、支持向量机［7-11］等计算机智能方法。传统需水预测方法具有便捷快速、适用性强等优点，计算机智能算法具有预测精度高、运算速度快等优点。但是，传统预测方法主观性较强，而人工智能方法容易陷入局部最优［12］，且机理不明。上述二者都不能从机理层面反映社会经济发展影响下用水结构和用水特点的变化［13］，无法描述经济-社会-生态需水系统的内在运行规律，导致中长期需水预测结果无法与区域经济社会的动态发展相适应。系统动力学模型可通过构建水-社会-经济-生态复杂系统各变量之间的相互关系，直观而完整的表现系统中需水量发展变化的动态过程［14］。

作为长三角一体化战略的组成部分和“一带一路”的重要节点，义乌市是新时期下我国工业城市产业结构升级转型加快的重要范本。城市升转型造成了义乌市用水形势的深刻变化，也为未来不同发展情景下的需水预测及水资源供需平衡分析提出了更高要求。本文以义乌市为例，采用系统动力学模型，通过设置48 种未来经济-社会-环境耦合需水情景，对区域2020-2050年的需水量进行预测。在此基础上，增加3 种再生水回用组合情景，对得到的144种供需情景进行比选，选出有利于水安全保障和区域生态环境可持续发展的6 种组合情景，以及适用于极端缺水情况的6 种组合情景，为中长期水资源规划和决策者提供科学依据和可选方案集。

1 系统动力学简介

系统动力学（System Dynamics，简称SD）由美国麻省理工学院Jay W Forrester教授于1956年创立［15］。它以控制论为理论基础，强调必须在了解内部结构组成的前提下，挖掘系统各部门相互交叉作用，把握参数物理意义及合理取值范围，从内部寻找行为发生的原因和发展方向，通过计算机仿真模型对实际系统进行模拟预测［16］。系统动力学模型理论的特性与水资源管理中各区域、各部门对水资源的需求量相互影响、相互作用、相互制约的关系相符合，因此系统动力学可应用于需水预测［17］，基于系统动力学的需水预测是从整体出发，根据水资源系统中各变量之间的因果和动态关系，构建水-社会-经济-生态耦合系统，综合考虑各子系统内各种因素之间以及不同子系统间各因素之间的相互作用，从水资源系统内部寻找行为发生的原因和发展方向，是一种定性与定量相互结合的方式［18］。

2 需水预测SD模型建立

2.1 建模目的

本文通过建立义乌市水资源供需平衡系统动力学模型，模拟预测2020-2050年义乌市总需水量以及总缺水量，动态反映未来社会经济发展对义乌市用水特点的影响，综合考虑生活、工业、农业和生态部门的用水需求，为未来长期的水资源高效开发利用和优化配置提供科学依据。

2.2 模型边界确定

系统边界指在问题的研究中涉及的各种因素，即系统变量。本文根据模型边界确定原则，结合义乌市规划资料，了解水资源供需系统的过程，结合水文系统、社会系统、经济系统和生态系统三者之间的耦合关系，分析关键因素，确定系统边界及变量类型，具体结果见表1。

表1 模型变量Tab.1 Model variables

从义乌市水资源供需系统内在变量之间逻辑关系和数据可获得性两个角度出发，依据两个系统变量的确定原则，共确定系统变量68 个，其中状态变量4 个、速率变量1 个、常量6 个、辅助变量57 个。其中，状态变量表示累积效应的变量，速率变量表示累计效应变化快慢的速度变量，辅助变量表示从积累效应变量到变化速度变量及变化速度之间的中间变量，常量表示在所考虑的时间内变化甚微或相对不变化的那些系统参数视为常量。特别的，图2 中＜Time＞、＜工业增加值＞、＜三产增加值＞、＜建筑业增加值＞表示4 个隐藏变量。所谓隐藏变量，是指已经存在于系统中的变量，但由于相关因素距离较远等原因，为了使画图更方便，流程图更美观，将这些变量设置为隐藏变量。

2.3 模型构建

模型从义乌市实际情况出发，确定68 个系统变量，结合水文、社会、经济、生态系统四者之间的交互关系，充分考虑再生水的回用，构建系统动力学模型，通过设置多种组合发展情景，对义乌市未来30年的总需水量和缺水量变化过程进行预测。结合供水预测结果，对未来水资源供需平衡状态进行分析。

2.3.1 数据来源

依据2009-2018年《义乌市水资源公报》、《义乌市统计年鉴》，以及《义乌市水资源综合规划》、《义乌市水资源调查评价》、《义乌市域总体规划（2013-2030年）》、《义乌市智慧水务业务应用建设》确定系统动力学模型的各参数。

2.3.2 模型建立准则

模型的模拟期为2009-2050年，时间步长DT为1年。2018年为基准年，规划水平年为2020年、2030年和2050年，2009-2018年为模型验证期。

2.3.3 建立系统因果关系及流程图

本文从系统内资源、人口、经济、社会和环境及其相互作用和相互制约的关系入手，考察系统的层次性、时序性、动态性、边界性、可控性，确定系统边界。义乌市水资源供需系统由需水子系统、供水子系统、社会子系统、经济发展子系统、环境子系统构成，系统内各要素跨子系统相互影响、相互作用、相互制约，形成具有多重反馈的因果关系结构如图1。

基于义乌市水资源供需系统因果关系反馈环（图1），构建义乌市水资源供需平衡系统的SD 模型系统流程图如图2所示，水资源供需平衡系统主要包括需水端和供水端［20］，其中需水预测是根据区域经济社会发展的用水现状，推算未来区域总需水量，为水资源的规划管理、供需关系分析提供基础。需水预测主要包括生活需水量预测、农业需水量预测、二产需水量预测、三产需水量预测和生态需水量预测。供水端除考虑传统方法中地表水可供水量、地下水可供水量和其他水可供水量（主要为雨水），也结合义乌市高效利用再生水以解决资源型缺水的战略规划，将再生水作为重要水源纳入供水端的预测。

图1 义乌市水资源供需系统因果关系反馈环Fig.1 The casual relationship and feedback mechanism of water resources supply and demand system in Yiwu City

图2 义乌市水资源供需系统SD模型系统流程图Fig.2 Flow chart of SD model system of water resources supply and demand system in Yiwu City

2.4 模型内部算法及参数估计

2.4.1 马尔萨斯-逻辑回归人口预测模型

马尔萨斯-逻辑回归人口预测模型是对传统人口预测模型马尔萨斯人口增长模型的改进模型，该模型适用于资源对人口增长有所限制的地区，本文基于该模型进行人口预测［21］。

式中：r为人口自然增长率（由区域人口增长规划确定）；N为人口增长阈值（以实际人口值与预测值拟合最优为原则选取）；t为预见期（在此文为2030年和2050年）；t0为基准期（在此文为2018年）根据马尔萨斯-逻辑回归人口预测模型推算，2030年义乌市常住人口为247.50万人，2050年常住人口约为293.76万人。

2.4.2 城镇化率预测模型

2009-2018年采用实际城镇化率，2030、2050年通过设定不同的发展情景确定（S0 零方案，S1 低增长，S2 稳增长，S3 高增长）。其中，S0零方案为对照组，即保持现状水平年（2018年）义乌市的城镇化率77.61%不变，反映发展水平不变情况下未来的需水情况加以对照；S1低增长情景表示由于经济社会等因素导致城镇化水平增速较慢的发展情景；S2稳增长情景表示在现有基础和规划条件城镇化稳步发展的情景；S3高增长情景表示在政策、经济等各因素驱动下城市化进程高速发展的情景。

由于过去10年，义乌市大力推动城镇化建设，城镇化率在2009-2018年年均增速已处于较高水平，城镇化率年均增长率为3.62%。S1 低增长发展情境下，假设城镇化率增速为过去10年的20%，得到2030年和2050年的城镇化率分别为84.85%和92.09%；确定S2 稳增长发展情境下2030年城镇化率为规划预测值90%，按照该年均1.24%的增长速度的50%，得到2050年城镇化率为96.2%；以稳增长情景S2 为基础，预测S3 高增长情境下义乌市2030年、2050年城镇化率分别为95%和98%。

2.4.3 节水意识预测模型

在实际生活中，居民节水意识实际增长过程是非线性的。近年来，居民素质上升明显，节水意识处于快速提升阶段，但这种提升不是无节制的，到达一定程度时，上升速度逐渐放缓，呈现由快到慢的趋势，并逐渐趋近于节水意识上限。该过程与sigmoid 函数变化过程类似，通过对sigmoid 函数的改进，根据节水意识对生活用水量影响的量化关系，参考已有研究［22］，对节水意识数学模型做出如下定义：

式中：M为超参数；θ为节水意识增长率，依据义乌市水资源系统特点，设定M=0.05。

根据居民节水意识的高低，通过对增长率θ的不同取值，将需水预测情景分为无节水意识情景J0、低度节水意识情景J1、中度节水意识情景J2，和高度节水意识情景J3，计算得到2030年和2050年的节水意识参数K2030、K2050，以判断不同节水意识情景下2030年和2050年可能的需水情况，如表3所示。

表3 义乌市4种不同节水情景 %Tab.3 Four kinds of different water-saving scenarios in Yiwu City

2.4.4 定额预测模型

在定额预测模型中，采用回归分析法，对2009-2018年各用水部门定额的统计值进行分析计算，得到规划水平年各部门的用水定额。结合《义乌城市总体规划（2030）》和《义乌市水资源综合规划（2030）》确定2030年其他变量的取值，对于模型中的6个常量，采用2018年的实际统计值。

（1）生活需水量预测。

式中：au(t)为城镇居民人均年用水定额，m³/人；UWD(t)为城镇生活需水量；aR(t)为农村居民人均年用水定额，m³/人；RWD(t)为农村生活需水量；DWD(t)代表第t年的生活需水量，k为节水意识。

（2）农业需水量预测。

式中：Ai表示第i种作物的种植面积；Qi表示第i种作物的灌溉定额；ƞi 表示第i种作物的灌溉水利用系数，如图1 所示；A1、A2、A3分别代表水田、旱地和经济作物的种植面积；Q1、Q2、Q3分别为3 种作物的灌溉定额；ƞ1、ƞ2、ƞ3表示第3 种作物的灌溉水利用系数；A1i、A2i、A3i分别代表某一频率的林果地、草场、鱼塘灌溉（或补水）面积；S1i、S2i分别为大、小牲畜头数；E1、E2、E3分别为林果地、草场、鱼塘灌溉（或补水）净定额；γ为林牧渔业利用系数，由供水规划与节水规划方案确定；AWD1为农田灌溉需水量；AWD2为林牧渔业需水量；AWD 为农业需水量。

（3）二产需水量预测。

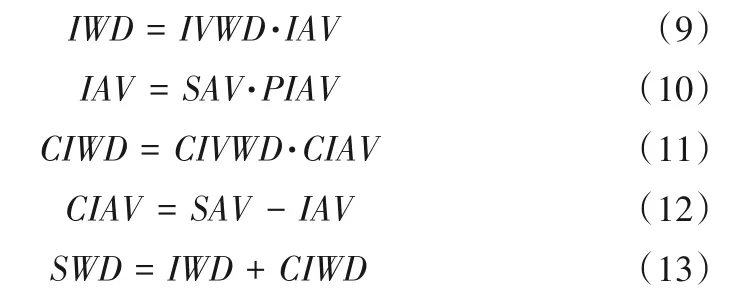
式中：SWD为二产需水量；IWD 为工业需水量；IVWD表示万元工业增加值用水量，该用水量与时间呈表函数关系；IAV为工业增加值；SAV为二产增加价值；PIAV为工业增加值占二产比例；CIWD为建筑业需水量；CIVWD表示万元建筑业增加值用水量，该用水量与时间呈表函数关系；CIAV为建筑业增加值，该值由二产增加值和工业增加值决定。

（4）三产需水量预测。

式中：TWD为三产需水量；TVWD为万元三产增加值需水量；TAV为三产增加值；GDP为国民生产总值；PTAV增加值占比，该比例为与时间有关的表函数。

（5）生态需水量预测。

式中：EWD为生态需水量；AAR为多年平均径流量；PEWD为规划百分比，该值为与时间有关的表函数，该规划百分比根据生态需水量与多年平均径流量的数量关系对历史序列取值。

根据生态需水量规划百分比取值的不同，将需水预测情景分为E0 零生态方案、E1 生态稳定方案、E2 生态高质量发展方案，如表4所示。

表4 义乌市3种不同生态情景 %Tab.4 Three different water-saving scenarios in Yiwu city

（5）可供水量预测。

式中：AWS为可供水量；ASWS为地表可供水量；AUWS为地下可供水量；OAWS其他可供水量；RAWS为再生水量；DWD为生活污水排放量；DWDR为生活污水治理率；IWD为工业污水排放量；IWDR为工业污水治理率；SRR为再生水回用率［23］。

污水资源化是解决水资源短缺的有效途径［24］。义乌市“十四五”规划中强调了将再生水作为重要水源，纳入水资源规划与配置。因此，本文根据污水回用率取值的不同，将供需平衡预测情景分为R1 低回用情景、R2 中回用情景（参考《义乌市城市总体规划》）和R3 高回用情景，对义乌市未来三十年水资源供需平衡状况进行分析，预测不同情境下的区域总缺水量，回用情景见表5。

表5 义乌市3种不同再生水回用情景 %Tab.5 Three different water-saving scenarios in Yiwu City

根据《义乌市水资源综合规划》，以现状工况下全市水资源供需平衡分析成果为基础，采用长系列调算法分析设计保证率下现状水平年义乌市可供水量为2.82 亿m3。义乌市境内水库水源挖潜包括调整八都、巧溪、岩口、长堰、柏峰、枫坑等6 座中型水库功能为城乡供水，建设上溪水厂、义南水厂与主城区城北水厂和义驾山水厂的连接干管，实现城乡一体化供水等措施。上述措施可增加优质水可供水量1 752 万m3。同时规划于后宅街道新建前傅水库，为主城区内科创新区提供优质水资源，规划水库集水面积1.45 km2，多年平均来水量110 万m3，正常库容65 万m3，95%保证率下优质水可供水量为70 万m3；于苏溪镇新建里深塘水库，为科创新区提供优质水资源，规划水库集水面积0.31 km2，多年平均来水量25 万m3，正常库容25 万m3，95%保证率下优质水可供水量为15 万m3；于廿三里街道新建鲍寺坑水库，为义东区提供优质水资源，规划水库集水面积2.88 km2，多年平均来水量220 万m3，兴利库容170 万m3，95%保证率下优质水可供水量为150 万m3。根据新版总规及《义乌市水利发展十三五规划》等，规划义乌江水源挖潜工程主要指双江湖水利枢纽工程。工程位于义乌江与南江汇合口下游2 km处，用于主城区、义南区及义西区工业用水和市政景观用水。双江湖规划水深4 m，水域面积4.5 km²，库容1 700 万m3，90%保证率下可新增年供水量7 300 万m3。上述工程措施已于2020年前完工。根据新版总规，境外引水工程主要包括金华安地水厂引水工程和九峰、安地水厂联合引水工程。其中2020年实施安地水厂引水工程，年引水量3 000 万m3；2030年实施九峰和安地水厂联合引水工程，年引水量5 000 万m3；合计引水量可达8 000 万m3。据相关研究成果，污水处理厂污水处理量的50%～70%可做回用处理，本次规划取50%。根据义乌市主要污水处理厂现状及规划（2020年）处理规模，估算义乌市污水处理可回用水量。根据上述对境内水库水源挖潜、义乌江水源挖潜、境外引水与中水回用等水资源开发利用方案所增加的可供水量分析成果，得到2030年规划水平年义乌市可供水量为3.54亿m³。在2030年可供水量预测基础上，充分考虑已成供水工程经过挖潜、改造、配套及水量的合理调配后新增加的可供水量，而且考虑了工程老化、损坏、淤积等因素对其供水能力的衰减影响。新建、续建工程，在考虑规划水源工程后，根据工程计划实施进度、资金投入程度、配套完善程度等分析其在规划水平年可能达到的供水量，依据义乌市多年平均实际供水增长率，预测得到2050年义乌市可供水量约为4.86 亿m³（此处为最大可供水量，不考虑极端异常气候情况和2030-2050年间新增供水工程建设情况）。

表6 义乌市需水预测模型参数设定Tab.6 Parameter setting of Yiwu water demand prediction model

2.5 模型检验

2.5.1 直观检验

通过分析系统因果关系和SD 流图，检验模型的驱动机制完善、结构设置合理，方程表述正确，量纲统一，通过系统动力学方法直观检验。

2.5.2 有效性检验

有效性检验是在模型直观检验通过后通过对模型进行模拟［13］，将模拟值与历史真实值数据进行对比，根据二者的偏差和符合程度，判断模型模拟的有效性。本文选择总需水量和国内生产总值两个关键变量，采用2009-2018年的历史统计数据对模型模拟值进行有效性检验（表7）。

由表7可知，实际值与模拟值相比，相对误差的绝对值基本都小于10%，就10年的验证期来说（以往研究多为5年以内［25，26］），与已有研究相比，模型的模拟值与真实值属于拟合较好的情况，模型模拟结果是可靠的。

表7 模型有效性检验Tab.7 Validity test of the model

2.5.3 稳定性检验

稳定性检验的方法为步长检验，通过设置不同的步长进行仿真，对比仿真结果，如果变化趋势基本一致，则表明模型不会产生病态结果。

如图3 所示，对模型设置不同的步长进行仿真可以看出选取不同步长的仿真结果变化趋势基本一致，模型具有较好的稳定性。

图3 不同步长国内生产总值仿真结果Fig.3 Different step sizes of GDP simulation results

3 义乌市需水预测结果及供需平衡结果分析

3.1 组合情景方案

以往对需水预测和水资源供需平衡关系的研究，多设置少数几个特定情景［27，28］，无法准确完善的反映需水量和供水量在各种不同条件下未来可能发生的变化。且这种情景设置的方式，也无法反映各因子动态变化对区域需水量和供需平衡状态可能带来的影响。

单一因子的变化无法真实反映未来在社会进步、经济发展和生态文明建设三者驱动下的用水特点的复杂变化［29］。因此，本文通过组合各影响因子梯度变化的方式得到多种组合情景。如表2～4所示，通过设置城镇化率参数、节水意识参数和生态发展参数的梯度变化，反映经济社会发展和生态文明建设需求对需水特点的影响，得到未来可能出现的需水组合情景共4 × 4 ×3= 48 种。在48 个需水组合情景的基础上，增加R1（低回用）、R2 中回用和R3 高回用三种再生水回用情景，得到共48× 3=144个水资源供需平衡分析组合情景。为义乌市未来将再生水作为重要水源纳入规划，构建新的供需平衡关系提供分析方法和决策指导。多种组合情景的设置可清楚反映未来各因子动态变化对区域需水量和供需平衡状态可能带来的影响，为决策者提供更加全面和为完善的决策依据。所有组合情景方案如图4所示。

表2 义乌市4种不同社会发展情景 %Tab.2 Four kinds of different social development scenarios in Yiwu City

图4 多方案组合情景设置Fig.4 Multiple combination scenario settings

3.2 情景方案优选

采用上文构建的义乌市系统动力学水资源供需平衡预测模型，对144 种组合情景进行模拟，得到各组合情景2009-2050年的缺水量。由于数据量较大，为方便数据分析，提取各组合情景2020年、2030年、2040年和2050年的缺水量作为各组合情景的缺水量代表值，进行进一步分析。为将144 个组合情景方案在2020年、2030年、2040年和2050年的表现作为一个整体评判，筛选出缺水量整体较少的组合情景方案，需对SD 模型模拟得到的缺水量代表值进行数据标准化处理，处理方法如公式（19）。

式中：i代表第i种水资源供需平衡分析组合情景；t表示缺水量预测的代表年份，分别为2020年、2030年、2040年和2050年；表示归一化处理后得到第i方案第t年的新的缺水量指标表示第i方案第t年的缺水量模拟值表示第t年所有方案中缺水量模拟值最小方案的缺水量表示第t年所有方案中缺水量模拟值最大方案的缺水量代表第i方案在第t年相对于该年的其他所有方案的缺水水平，越大表示相对其他方案来说该方案缺水情况较严重。

为分析在未来中长期范围内各组合情景的缺水量水平相对于其他方案是否有所改善，将2020年标准化后的各方案缺水量值作为横坐标值，即将2020年该方案在所有方案中的缺水水平作为参考系，将2030年、2040年和2050年的值作为纵坐标值得到共144 × 3= 432个点，每个点代表各组合情景在各年份的缺水量。如图5 所示，依据所有方案在不同水平年的缺水量的值，对组合情景方案进行初步筛选。

如图5所示，第一轮筛选中，为满足社会发展的用水保障需求，得到未来中长期时段内总缺水量较小的方案，丢弃缺水量在平均水平以上的方案，即纵坐标大于0.5的所有点。如图5所示，Ⅰ区和Ⅳ区的所有组合情景点总缺水量标准值小于0.5，总缺水量在所有组合情景中相对较小，保留这些组合情景点共56个。

图5 144种组合情景方案筛选Fig.5 Screening of 144 combinations of scenarios

第二轮筛选过程中，考虑两点筛选原则。一是考虑某一种方案相对于该年份的所有方案，其排名位置在规划水平年的缺水水平相对于2020年是否有所改善即将2020年该方案的缺水量排名位置作为基准值，将规划水平年（2030年、2050年）的缺水量标准化值与之相比，观察该方案相对于其他所有方案而言排名位置在未来是否有所改善，即该方案的动态发展是否优于其他方案。若该比值小于1，说明该方案相对于其他方案的缺水量排名较2020年有所提高，即图4 中Ⅰ区域。二是考虑规划水平年各方案总缺水量的大小，筛选出各规划水平年缺水量小于所有方案该年缺水量均值的方案。综合以上两点筛选原则，第二轮筛选得到32个组合方案。

第三轮筛选中，如图6 所示对第二轮筛选得到的32 个组合情景方案2020年、2030年、2040年和2050年的总需水量排序，将各个年份总需水量小于均值的20个组合情景作为A 区，将大于均值的12 个方案作为B 区。在A 区方案集中选择需水量最少，且城镇化率发展情景不为S0 的方案共6 个组合方案组成A方案集合，A 方案集合代表了社会经济取得一定发展条件下若出现极端缺水情况时需水量最少的组合方案，该方案集合中的优选方案有利于应对未来可能出现的极端缺水情况。依据该筛选条件，在A 区筛选得到的组合方案有：S1J3EOR2、S1J3EOR3、S2J3EOR2、S2J3EOR3、S3J3EOR2、S3J3EOR3；在B区方案集中选择需水量较少，城镇化率发展情景不为S0，生态发展情景不为E0 的方案共6 个组成B 方案集合，B 方案集合代表所有情景方案中需水量较小，生态较为友好，且综合考虑了社会经济不同发展水平的组合方案，该方案集合适用于非极端缺水条件下，保障区域水安全和社会-经济-生态环境系统可持续发展。依据该筛选条件，在B 区筛选得到的组合方案有：S1J3E1R3、 S2J3E1R3、 S3J3E1R3、 S1J2E1R3、 S2J2E1R3、S3J2E1R3。

图6 第一轮筛选所得56个情景缺水总量Fig.6 Total water shortage of 56 scenarios in the first round of screening

3.3 决策方案对比

如图8、9 所示，A、B 方案集各方案的总需水量在2018年之后稳步升高，A 方案集总需水量和缺水量整体小于B方案集合，B方案集中各方案总缺水量较A 方案集差异明显。值得注意的是，在A方案集中所有组合方案均为高度节水（J3）情景，而高回用（R3）和中回用（R2）情景各占一半，这表明在极端缺水条件下，提高居民节水意识的重要性相对提高再生水回用率更为重要。但是在B 方案集中，筛选出的所有组合方案均为高回用情景，高度节水情景和中度节水情景各占一半，这表明在依据该筛选条件，在保障区域水安全和社会-经济-生态环境系统可持续发展的综合要求下，且来水量正常条件下，提高再生水回用率较提高居民节水意识，对改善水资源供需关系更为有效。在A方案集中，S1J3E0R2和S1J3E0R3总需水量最少，在2030年和2050年均为3.68和6.07 亿m³；S3J3E0R2和S3J3E0R3 总需水量最多，在规划水平年需水量均为3.77、6.12 亿m³；S3J3E0R3总缺水量最少，规划水平年缺水量分别为0.24、1.26 亿m³；总缺水量最大的组合情景为S1J3E0R2，规划水平年缺水量分别为0.67和2.04 亿m³。B 方案集中，需水量最小的组合情景为S1J3E1R3，规划水平年需水量分别为4.42和7.17 亿m³；需水量最大的组合情景为S3J2E1R3，规划水平年需水量分别为4.54、7.51 亿m³；缺水量最小的组合情景为S3J3E1R3，规划水平年缺水量分别为0.97、2.36 亿m³；缺水量最大的组合情景为S1J2E1R3，规划水平年缺水量分别为1.00、2.70 亿m³。综上，A、B 方案集中，2030年和2050年总缺水量最小的方案相差0.73 和1.1 亿m³；总缺水量最大的方案相差0.33和0.66 亿m³。需要说明的是，该模型预测得到的各方案情境下的总需水量和总缺水量为不考虑新建或改建水源工程影响的模拟值。

图7 总需水量情景比选Fig.7 Total water demand scenarios comparison

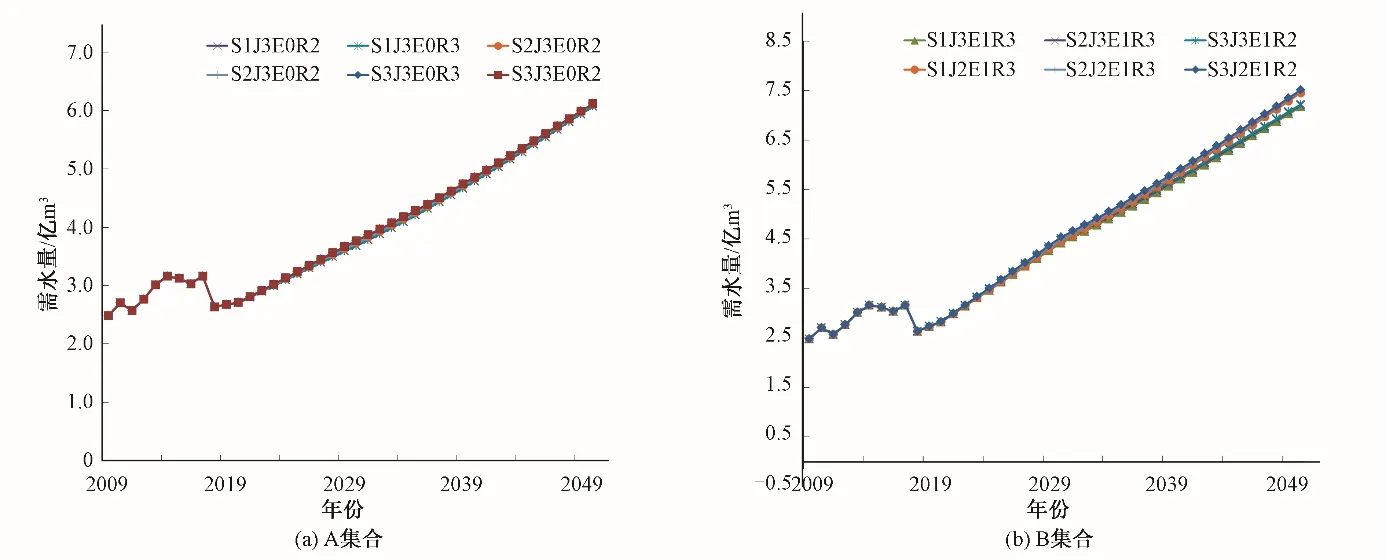
图8 优选方案总需水量变化过程Fig.8 Change process of the total water demand of the optimal scheme

图9 优选方案总缺水量变化过程Fig.9 Change process of the total water shortage in the optimal scheme

若未来中长期时段内，区域降水显著减少，处于严重资源型缺水状态，为降低区域缺水风险，可参考A 集合中的各组合方案，适当降低生态要求，优先保证生活和生产用水，从提高节水意识和再生水回用率两个角度减少缺水量，节水重点在于提高居民节水意识。若需保障区域水安全和社会-经济-生态环境系统可持续发展，可在B 集合中根据实际情况选择组合情景方案进行需水量预测和水资源供需平衡分析。在此基础上，将再生水回用率以及居民节水意识两个角度作为突破口，节水重点在于提高再生水回用率，参考方案B中二者的组合情景，获得不同节水意识和再生水回用率水平下未来30年的总需水量和缺水量，作为水资源中长期规划和节水战略决策的科学依据。A方案集合和B方案集合针对不同的情景，通过方案优选，从不同角度为决策者提供决策支持。决策者可根据实际情况选取组合情景方案，采用本文构建的系统动力学模型，得到义乌市未来不同情景下的缺水量和需水量。

4 结 论

本文从义乌市实际情况出发，确定68 个系统变量，结合水文、社会、经济、生态系统四者之间的交互关系，充分考虑再生水的回用，构建系统动力学模型。通过设置48 种未来经济-社会-环境耦合需水情景，对区域2020-2050年的需水量进行预测。在此基础上，增加3 种再生水回用组合情景，对得到的144种供需情景三轮方案根据不同发展要求和来水条件进行比选，选出A、B 两个方案集。其中一个方案集包括义乌市极端缺水情况适用的6 种组合情景，另一个方案集包括最有利于区域水安全保障和生态环境可持续发展的6种组合情景。这些组合情景为中长期水资源规划和决策提供科学依据和可选方案集。

（1）系统动力学方法可用于模拟预测复杂水资源系统未来中长期时段内区域总需水量以及总缺水量，动态反映未来社会经济发展对区域用水特点的影响，综合考虑了生活、工业、农业和生态部门的用水需求，为未来长期的水资源高效开发利用和优化配置提供科学依据。

（2）义乌市属于资源型缺水城市，提高再生水回用率可有效缓解该市用水紧张问题，在2030年和2050年将再生水回用率分别提高至60%和90%，可将总缺水量最大程度降低到0.24和1.26亿m³。

（3）多因子梯度变化驱动下的组合水资源供需情景设置，可为决策者提高更加全面的决策支持。本文通过方案优选对比发现，未来中长期时段内，再生水回用率对义乌市最有利于区域水安全保障和生态环境可持续发展的6种组合情景的总缺水量影响较大，居民节水意识对极度缺水条件下的水资源供需关系影响相对较大。 □