不同山葡萄品种光响应模型拟合及综合评价

刘阳阳，潘越，王世伟，虎海防

（1.新疆农业大学林学与园艺学院，乌鲁木齐 830052；2.新疆林业科学院园林绿化研究所，乌鲁木齐 830063）

新疆是我国最大的葡萄产区，具有独特的生态环境和区位优势，与法国波尔多、美国加利福尼亚并称为“世界三大黄金葡萄产区”。2018年新疆酿酒葡萄的栽培面积为3.25×104hm2，产量达32.08×107kg，高居全国第一［1-2］。近年来，由于投入不足、管理粗放、病虫害等问题，导致葡萄产量和品质降低，经济效益受损严重［3-4］。野生山葡萄（Vitisamurensis）原产于我国东北及华北地区，属葡萄科葡萄属藤本植物，具有抗寒性强、产量高、酒质好等特点。我国山葡萄自然资源集中分布于北纬40°—45°，不同区域共收集保存了365份山葡萄杂交种质资源［5］，并已在东北和内蒙古等地区大量推广种植［6-8］。新疆恰好处于山葡萄适宜种植区，气候条件优越［9-10］，因此，引入山葡萄品种在新疆种植对完善新疆酿酒葡萄资源类型、提高农户种植热情和经济收益具有重要意义。

根据植物对光照强度变化的敏感度及响应方式，提出借助直角双曲线模型［11］、非直角双曲线模型［12］、指数模型［13］和直角双曲线修正模型［14］对光响应参数进行拟合，以达到提高模拟准确度的目的，现已被大量应用于苹果［15］、混生地被竹［16］和山杏［17］等资源的评价。关于山葡萄光响应模型的筛选评价，国内尚未见报道，为此，本研究选取了6个山葡萄品种，在同质环境条件下，运用因子分析法利用4种模型的光响应曲线进行拟合，筛选光能利用效果最佳的山葡萄品种和最适光响应模型，旨在完善山葡萄评价体系，为山葡萄在新疆的推广利用提供技术参考。

1 材料与方法

1.1 试验地概况

试验地位于新疆阿克苏地区温宿县新疆林科院佳木试验站，占地面积80 hm2，海拔1 103.8 m，地下水深度2.8～3.3 m；属温带干旱气候，昼夜温差大，多大风降温天气，时常有倒春寒现象发生，夏季炎热而干燥，蒸发量大，年均降水量不足100 mm，年均气温10.1℃，极端低温-27.4℃，年均日照时数2 747.7 h，≥10℃年积温2 916.8～3 198.6℃，无霜期205～219 d。

1.2 试验材料

选取‘北冰红’‘双红’‘左优红’‘雪兰红’‘北国红’和‘双丰’6个山葡萄品种为供试材料，以‘威代尔’为对照（CK），于2019年秋季定植，选用2 a生苗木，南北行向定植，单臂篱架，田间正常肥水管理，株行距为1 m×3.5 m。

1.3 试验方法

每个品种挑选3株长势一致的植株作为3个重复，分别于2020年8月5日、7日和10日（葡萄转色期）11：00—13：00，以主蔓基部向上第8～10片成熟完整的功能叶为测定对象，使用Li-6400便携式光合仪（美国LI-COR公司生产），设定红蓝光光合有效辐射（photosynthetically active radiation，PAR）梯度为1 900、1 700、1 500、1 200、1 000、800、500、300、200、150、100、80、50、20和0 μmol·m-2·s-1共 15 个处理。改变光照强度后，最少稳定时间设定为120 s，当测量结果变异率小于0.05 s时，由仪器自动记录。测定时为保持环境的稳定性，叶室CO2浓度设定为（380±10）μmol·mol-1，叶温为（32±1）℃，湿度为自然 RH。通过光合电子流对光合作用和光响应结果建立光响应机理模型。进而绘制光响应曲线，计算光补偿点（light compensation point，LCP）、光饱和点（light saturation point，LSP）、表观量子效率（apparent quantum yield，α）、最大净光合速率（maximum net photosynthetic rate，Pnmax）和暗呼吸速率（dark respiration rate，Rdark）。

1.4 光响应模型拟合

利用非直角双曲线模型（non-rectangle hyperbola model，NH）［12，18］、直角双曲线模型（rectangular hyperbola model，RH）［11，19］、指数函数模型（exponential model，EF）［13］和直角双曲线修正模型（modified rectangular hyperbola model，MRH）［14，20-21］对山葡萄光响应参数进行模型拟合。

① 非直角双曲线模型拟合方程。

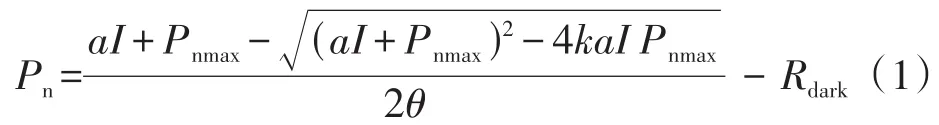
式中，Pn为净光合速率（μmol·m-2·s-1）；I为光合有效辐射（μmol·m-2·s-1）；Rdark为暗呼吸速率（μmol·m-2·s-1）；α为表观量子效率，是直线方程拟合弱光环境（≤200 μmol·m-2·s-1）的光响应，即光响应曲线初始斜率；Pnmax为最大净光合速率（μmol·m-2·s-1）；k为光响应曲线角（0≤k≤1）。

LCP为x轴与直线方程的交点（μmol·m-2·s-1）；LSP为直线方程与直线y=Pnmax的交点所对应x轴的数值（μmol·m-2·s-1）。二者的计算公式如下。

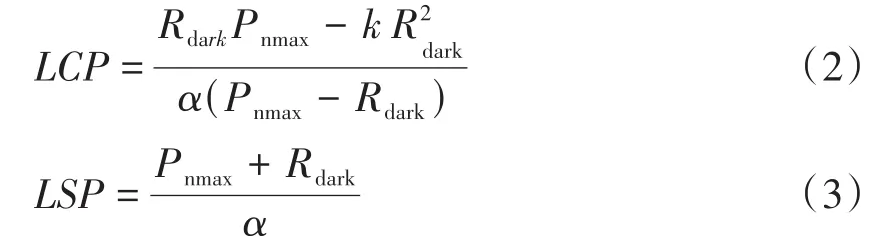
② 直角双曲线模型拟合方程。

式中，Pn、α、I、Pnmax和Rdark的定义与式（1）一致。

LCP和LSP计算方式与非直角双曲线模型一致。

③ 指数方程函数［13］拟合方程。

式中，Pn、α、I、Pnmax和Rdark的定义与式（1）一致；CD为弱光环境下净光合速率区域为0的指标。

LSP为光合速率为0.9Pnmax时所对应的光强；LCP为Pn为0时所对应的光强。

④ 直角双曲线修正模型［14，20-21］拟合方程。

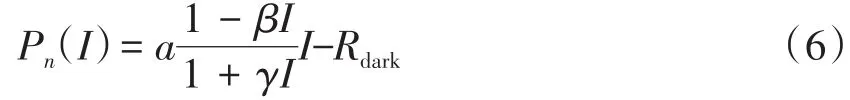
式中，Pn、α、I、Pnmax和Rdark的定义与式（1）一致，通过SPSS19.0计算α、β、γ和Rdark的值。

LSP根据以下公式计算。

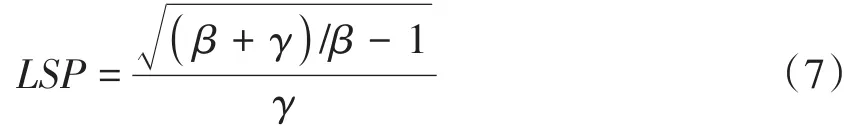
根据光饱和点计算Pnmax，公式如下。

将α、β、γ和Rdark的值带入方程，当Pn（I）=0时，求解I值即为LCP。

1.5 模型精准度评价

使用均方差法（root mean square error，RMSE）及平均绝对误差法（mean absolute error，MAE）对4个模型拟合结果的精准度进行评价，误差越趋近于0，表明拟合值越接近实测值［22］。计算方法见公式（9）、公式（10）。

式中，yt和分别是净光合速率的实测值和拟合值；n为样本数。

1.6 山葡萄品种综合评价

采用隶属函数法统一数量纲，指标α、Pnmax和LSP为正相关参数，采用公式（11）计算；LCP和Rday为负相关参数，采用公式（12）计算。

式（11）和（12）中，Uin、U′in分别为第n个样本第i个指标转化后的隶属函数值；Xin指第n个样本第i个指标的原始测定值；Ximax和Ximin分别指样本组中第i个指标的最大值与最小值。

利用标准化后的数据采用SPSS 22.0软件完成方差分析［23］和主成分分析［24］，提取出对光响应指标有显著影响的主成分，得出各成分的分值Fjn，以相应公因子的贡献率Ej为权重，计算综合分值Dn。

式中，Dn表示以主成分分析法得出的各样品光响应参数的综合分值；Fjn表示第n个样品第j个特征值＞1的主成分的分值；m为特征值＞1的主成分的个数；Ej为第j个主成分的贡献率。

将旋转载荷矩阵各主成分的载荷值除以对应主成分特征根可得得分矩阵，得分矩阵开算数平方根与标准化后的数据乘积即为各主成分的关系式，关系式分别如下。

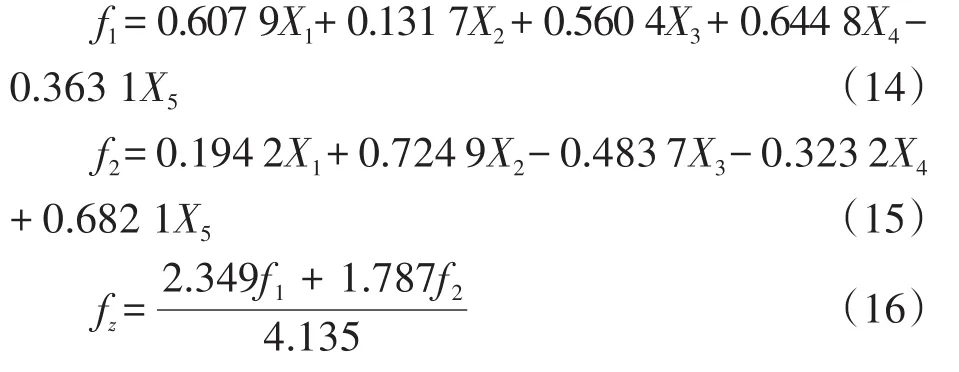
2 结果与分析

2.1 不同山葡萄品种的光合-光响应过程

不同山葡萄品种的光响应曲线结果（图1）表明，低光照强度条件下时（PAR≤80 μmol·m-2·s-1），除‘双丰’外，其他品种叶片的Pn对PAR表现均较为敏感，随着PAR的增加叶片Pn快速上升。当PAR＞80 μmol·m-2·s-1时，不同山葡萄品种表现出较大差异，如‘北冰红’和‘左优红’的叶片Pn增长最为显著。当PAR为 1 500～1 700 μmol·m-2·s-1时，各山葡萄品种的叶片Pn趋于平缓，区别在于‘左优红’的叶片Pn在PAR＞1 700 μmol·m-2·s-1时开始下降，而‘北冰红’叶片Pn仍呈上升趋势。‘威代尔’‘双红’‘雪兰红’和‘双丰’叶片Pn随着PAR的增加虽有所提高，但增幅均显著小于‘北冰红’和‘左优红’，当PAR为1 200～1 500 μmol·m-2·s-1时，表现出一定的光抑制现象。‘北国红’叶片Pn在PAR介于 80～1 500 μmol·m-2·s-1时增幅较小，但当PAR＞2 000 μmol·m-2·s-1时仍有上升趋势。综上所述，不同山葡萄品种的叶片Pn表现为‘北冰红’＞‘威代尔’＞‘左优红’＞‘双红’＞‘北国红’＞‘双丰’＞‘雪兰红’。北冰红’叶片Pn均值较‘威代尔’‘左优红’‘双红’‘北国红’‘双丰’和‘雪兰红’分别提高13.62%、17.42%、19.91%、32.67%、41.05%和43.51%。

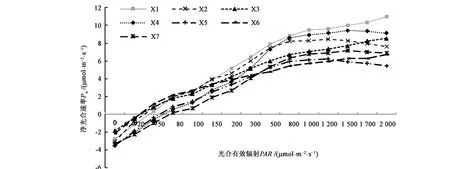
图1 不同山葡萄品种的光响应曲线Fig.1 Photoreactivity curves of different Vitis amurensis cultivation

2.2 不同光响应模型对光响应参数的影响

4种模型对不同山葡萄品种光响应拟合的参数见表1。表观量子效率（α）为光响应曲线的初始斜率，值的大小表示低光照强度下拟合曲线的准确度［25］。利用4种模型对7个山葡萄品种光响应进行拟合，各模型所得α值均小于0.125（表1），表明4种模型的拟合结果均在理论范围内。

决定系数（R2）反映了自变量误差与因变量之间的相关性［26］，取值为［0，1］，R2越大，说明曲线拟合效果越好，反之拟合精度越差。由表1可知，非直角双曲线模型在拟合‘北冰红’和直角双曲线模型在拟合‘左优红’时R2较低，分别为0.631 7和0.851 9；其他模型对各品种光响应过程拟合的R2均大于0.9，拟合精准度均较高，其中，直角双曲线修正模型对7个山葡萄品种光响应拟合的R2均最高。

暗呼吸速率（Rdark）为植物在暗光环境下消耗光合作用所产生有机物的值［20，27］。不同模型对Rdark的估算结果（表1）表明，直角双曲线修正模型对‘北冰红’‘双红’‘左优红’‘雪兰红’‘北国红’和‘双丰’的Rdark估算值与实测值最为接近；直角双曲线模型对‘威代尔’Rdark的估算值与实测值最接近；指数函数模型对山葡萄Rdark的估算值相较于实测值偏低；非直角双曲线模型对‘双红’‘左优红’‘雪兰红’‘北国红’和‘双丰’的Rdark估算值略高于实测值，但与直角双曲线修正模型拟合结果较为相近。

最大净光合速率（Pnmax）是指光强达到最大时植物的净光合速率［28］。直角双曲线模型、非直角双曲线模型和指数函数模型均能直接计算出各山葡萄品种叶片Pnmax，而直角双曲线修正模型（表1）不同，山葡萄品种叶片光合光响应曲线不同。模型的光响应特征值在拟合‘北冰红’‘双红’和‘北国红’时，参数β为负值，故In（μβ）无法计算，这一问题同样出现在青稞［29］、玉米［30］上，为此利用SPSS 22.0软件对Pnmax进行估算。不同模型的Pnmax估算结果（表1）表明，直角双曲线修正模型对‘威代尔’‘左优红’‘雪兰红’和‘双丰’叶片Pnmax估算值与实测值最相近；直角双曲线模型对‘北冰红’和‘北国红’叶片Pnmax估算值略高于实测值；其他模型的Pnmax估算值与实测值存在一定偏差。

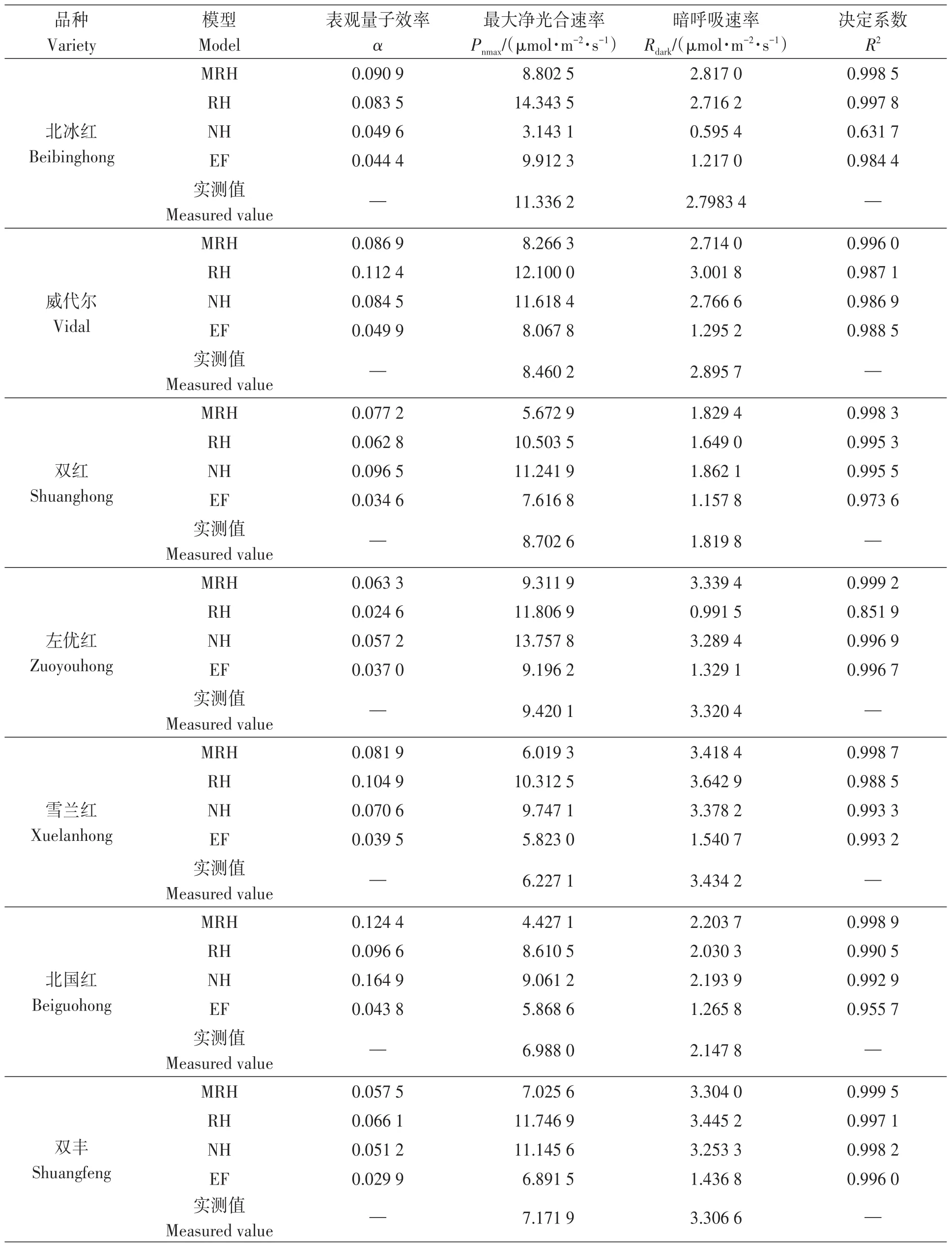
表1 不同山葡萄品种叶片光合光响应曲线不同模型的光响应特征值Table 1 Photosynthetic response characteristcs of Vitis amurensis leaves with different light response models

2.3 不同模型对光补偿点和光饱和点的影响

4种模型对7个山葡萄品种LCP和LSP的估算结果（表2）表明，非直角双曲线模型对‘北冰红’LCP的估算和指数函数对‘左优红’‘雪兰红’LCP的估算显著低于实测值，且LSP的估算结果均显著小于实测值，与田间实际调查结果差异较大。除‘北国红’外，直角双曲线修正模型对其余6个山葡萄品种LSP的估算值与实测值最为接近。由此可见，直角双曲线模型、非直角双曲线模型和指数函数模型不适用于山葡萄光饱和点的拟合；而直角双曲线修正模型能有效模拟光抑制情况，且所得估计值与田间实测值符合度较高。

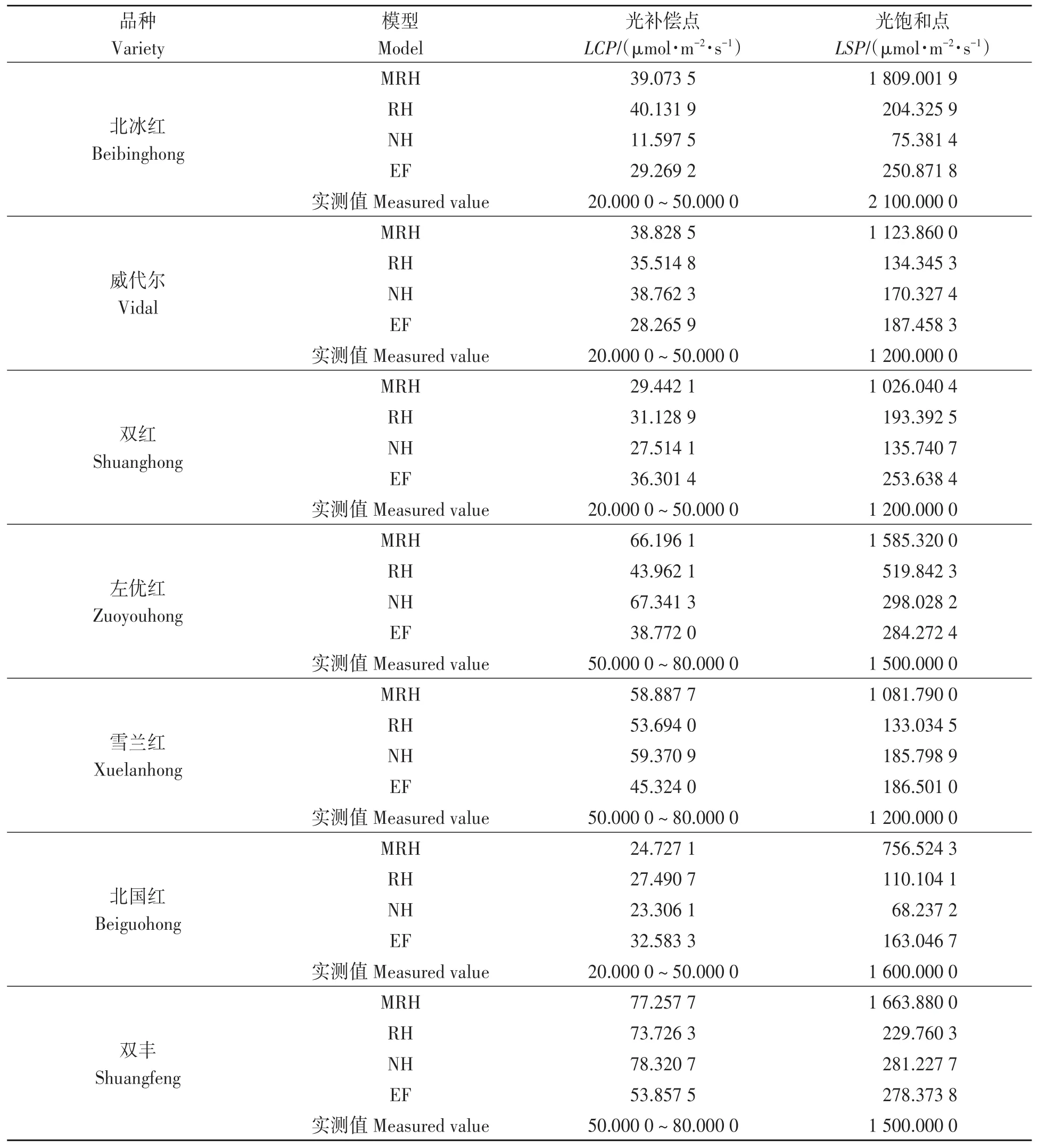
表2 不同光响应模型对山葡萄品种光补偿点和光饱和点Table 2 Light compensation point and light saturation point of Vitis amurensis by different light response models

2.4 不同模型拟合的光响应参数的比较

模型的均方差（RMSE）及平均标准误差（MAE）能够反映模型的拟合精度，RMSE和MAE值越趋近于0，R2越趋近于1，说明拟合精确度越高。4种模型的RMSE和MAE结果（表3）表明，不同模型对山葡萄光响应拟合时存在一定差异。其中，直角双曲线修正模型对各山葡萄品种光响应过程拟合的均值均最小、R2最大；非直角双曲线模型对除‘双丰’外的6个山葡萄品种的拟合效果仅次于直角双曲线修正模型；直角双曲线模型对‘双丰’的拟合效果仅次于直角双曲线修正模型，对‘北冰红’‘双红’和‘北国红’的拟合效果再次于非直角双曲线模型效果；指数函数模型对‘北冰红’‘左优红’和‘雪兰红’的拟合效果仅次于非直角双曲线模型。由此可见，直角双曲线修正模型为山葡萄光响应过程拟合的最优模型。

表3 不同光响应模型对山葡萄拟合优度比较Table 3 Comparison of the goodness of fit between different light response models

2.5 不同山葡萄品种的主成分分析

2.5.1 数据标准化 由于‘北国红’的LSP实测值与光响应模型拟合结果差异较大，因此在后续分析时予以剔除。

各个光响应参数的数量纲不一致，使得评价不具有可比性及统一性，因而在进行主成分分析前对数据进行标准化处理［31］。标准化后的数据结果见表4。经KMO和Bartlett球形检验，显著性为0.093，满足进行下一步分析的要求。

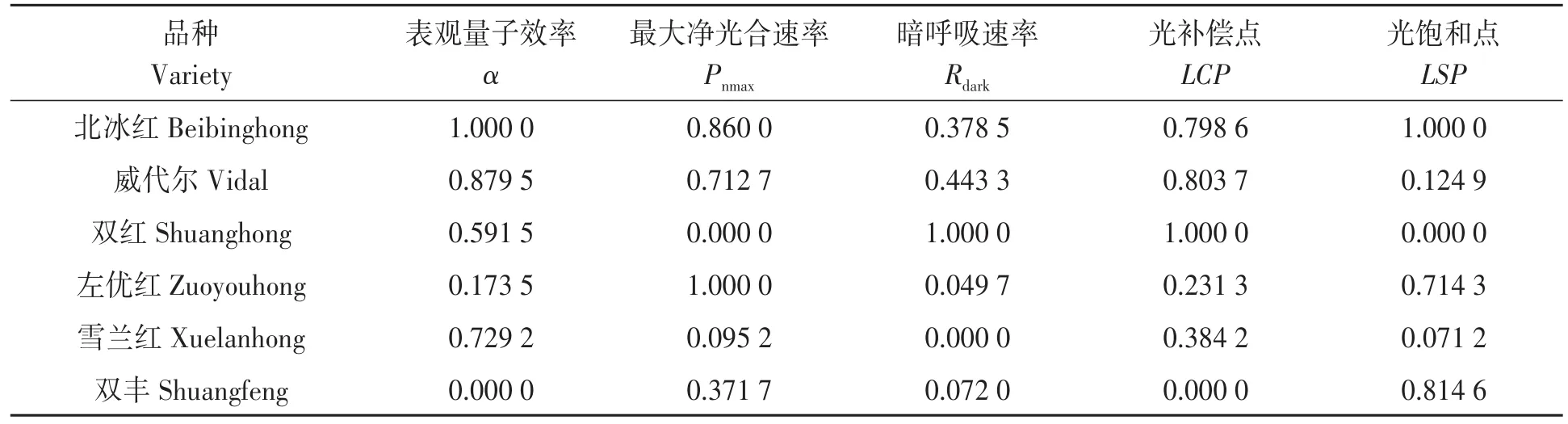
表4 山葡萄光响应参数标准化的结果Table 4 Result of standardization of light response parameters of Vitis amurensis

2.5.2 主成分分析 对标准化后的数据进行主成分分析，结果（表5）表明，从5项光响应参数中提取出2个特征根＞1的主成分，其中，第1主成分的贡献率为46.973%，第2主成分的贡献率为35.736%，两个主成分的累计贡献率达82.710%。第1主成分（f1）中载荷值较大且为正的指标有表观量子效率（α）、光补偿点（LCP）和暗呼吸速率（Rdark），载荷值分别是0.868、0.977和 0.738，主要反映暗光条件下叶片对弱光的适应能力，因此命名为弱光环境因子；第2主成分（f2）载荷值较大且为正的指标为光饱和点（LSP）和最大净光合速率（Pnmax），载荷值分别为0.831和0.939，主要反映叶片对强光的利用能力和植物的最大光合潜力，因而命名为强光环境因子。

表5 旋转后的主成分载荷矩阵Table 5 Principal component load matrix after rotation

2.5.3 不同山葡萄品种的综合评价 对6个山葡萄品种进行综合评价（表6），根据暗光环境因子f1排序为‘双红’＞‘威代尔’（CK）＞‘北冰红’＞‘雪兰红’＞‘左优红’＞‘双丰’。其中，‘双红’得分最高，暗呼吸速率Rdark和光补偿点LCP最高，该品种的优势在于适应荫蔽环境能力较强，且在暗光环境中呼吸消耗少；‘北冰红’排名居中，值得注意的是‘北冰红’光能利用效率α最高，说明该品种光能转化效率较高；‘双丰’排名最低，得分为负，即在弱光环境下光能利用效率低，呼吸消耗较大。根据强光环境因子f2排序为‘左优红’＞‘北冰红’＞‘双丰’＞‘威代尔’（CK）＞‘雪兰红’＞‘双红’，表明‘左优红’和‘北冰红’对强光环境的适应能力较强，在强光环境下不会受到光抑制，且在日照充裕的地区，光合作用制造的碳水化合物较多，枝条养分储备充足。综合排名fz由高到低排序依次为：‘北冰红’‘威代尔’‘双红’‘左优红’‘雪兰红’和‘双丰’，‘北冰红’得分最高，在强光环境和弱光环境均表现较好。

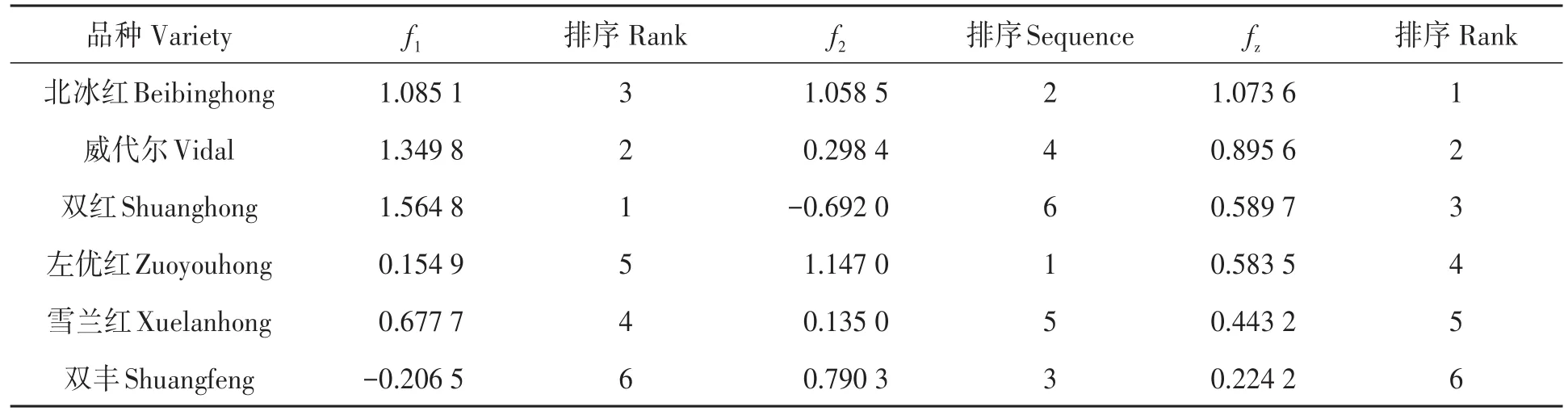
表6 不同品种的得分和综合得分Table 6 Scores and composite scores of different varieties

2.6 不同山葡萄品种的聚类分析

为使光响应参数指标相近的山葡萄品种归为一类，采用Ward聚类分析法加以区分［31］，图2中可以看出，第1类包括‘左优红’和‘双丰’，这2个品种α较低，Rdark、Pnmax和LSP较高；第2类包括‘北冰红’和‘威代尔’，这两个品种α和Pnmax较高，但LCP较低，Rdark中等，体现了较强的高光能利用效率，弱光效果不明显；第3类包括‘双红’和‘雪兰红’，这两个品种α居中，Rdark和LSP较低。

图2 聚类分析谱系Fig.2 Cluster analysis pedigree

3 讨论

大量研究表明，光响应模型的选取在不同品种间存在较大差异［35］。目前，直角双曲线模型、非直角双曲线模型和直角双曲线修正模型等众多数学模型被广泛用于植物光响应曲线的拟合［21，36］。不同模型对同一植物或同一模型对不同植物在拟合过程中存在差异性，为此，筛选合适的光响应模型显得尤为重要。本研究表明，4个光响应模型对山葡萄光响应拟合时均与实测值存在一定偏差，其中，直角双曲线模型在拟合‘北冰红’Pnmax和Rdark时与实测值最相近，指数函数在拟合‘双红’Pnmax时最趋近于实测值。但单一某个生理参数只能评价该模型的一个方面［11，16-17，37］，在选择模型时应考虑模型的整体拟合效果［14，17-18］。为此，综合分析表明，直角双曲线修正模型对山葡萄光响应拟合的RMSE、MAE最小，R2均达到0.99以上，明显高于直角双曲线模型、非直角双曲线模型和指数函数模型，可作为山葡萄光响应拟合的最佳模型，与夏江宝等［35］、李玉洁等［23］研究结果相一致。直角双曲线模型、非直角双曲线模型和指数函数模型属于没有极值的函数模型，无法直接计算LSP，SPSS线性回归所得LSP比实测值明显偏低，表明这3种模型对山葡萄光响应拟合时存在一定缺陷。

考虑到光响应参数指标的单位不一致，因此，本研究对各参数数据进行了标准化处理。利用标准化后的数据进行主成分分析，从5项参数指标中提取到2个主成分因子，因子间相互独立，避免了信息的干扰，有利于山葡萄品种的综合评价［24］。5个山葡萄品种及对照（CK）综合得分为：‘北冰红’＞‘威代尔’＞‘双红’＞‘左优红’＞‘雪兰红’＞‘双丰’。主成分分析法既能客观地筛选出综合表现良好的山葡萄品种，还能按照光响应类别分别对山葡萄进行评价。通过聚类分析显示，‘左优红’和‘双丰’具备阳生植物特性，光合潜力巨大，但在弱光环境下呼吸消耗较高，因此适合在日照时间充裕、光照较强的地区推广；‘北冰红’和‘威代尔’表现出较高光能利用效率，但弱光环境表现一般，并且‘威代尔’的LSP值较低，一方面可能是品种特性所致，另一方面可能是由于测定时间段内阴雨天较多，叶幕光截获效率未能有效释放，导致光合潜力没有充分发挥［32］；‘双红’和‘雪兰红’在弱光环境下可通过减少暗呼吸速率的消耗使植物体维持稳定状态。不同山葡萄品种在LCP、LSP、Pnmax、Rdark和α均存在较大差异，这可能是由于不同品种吸收同化养分的能力不同，且不同品种内源激素水平和生理代谢产物不同［17，26］。因此在品种推广过程中，应结合各地自然生态条件有选择的栽植。