边坡危险滑动面及稳定安全系数的力学解析方法*

吕爱钟 贾晓阳

(华北电力大学水利与水电工程学院， 北京 102206， 中国)

0 引 言

边坡稳定问题是岩土力学领域的一大经典问题，近百年来，学者们提出了一系列的稳定性分析方法。

最早提出的瑞典圆弧法(Fellenius， 1936)假设边坡的滑动面为圆弧面，在发生滑动破坏时滑动面上达到Mohr-Coulomb 强度准则的极限状态，在进行计算时，需要将滑动体垂直分成若干条块，并将条块视为刚体，通过假定条块间的内力，列出静力平衡方程对边坡稳定安全系数进行求解。这也就是经典极限平衡法的理论基础，基于这一原理和不同的条块间内力的假定，Bishop(1955)、Morgenstern et al. (1965)、Janbu(1973)、Sarma(1973)等研究者们提出了一系列的极限平衡稳定性分析方法。几十年来，极限平衡法因其计算简单并且适用范围广，迅速衍生出了一系列改进的分析方法。Maslov(1990)、Zhu et al. (2003)、Zheng(2009)基于滑动面正应力分布的假设，先后提出了满足平衡条件而且不需要将滑动体进行竖向分割的分析方法。陈祖煜等(2001)、朱大勇等(2007)和郑宏(2007)先后提出了边坡的三维极限平衡计算方法。

以往的极限平衡条分法在被广泛应用的同时，也暴露出其理论上的缺陷，例如：在分析中认为边坡体是不可变形的刚体，这显然是不符合实际的； 对条块间内力或者对滑动面上正应力分布的假定，以及对滑动面形状假定的是否合理？计算中只求解了平衡方程，所得结果是否满足变形协调方程？这是经典极限平衡法无法问答的问题(Lu et al.，2012)。

随着计算机技术的发展，有限元法等数值方法在力学计算领域得到了广泛应用，这种将物体微元化的求解方法不仅满足平衡方程而且还兼顾了变形协调方程，研究者们也将这种适用性很广的方法引入到了边坡稳定性分析问题中，但是传统的有限元法不能直接求得边坡的稳定安全系数。Giam et al. (1988)提出了一种根据有限元法计算应力场确定临界滑动面及最小稳定安全系数的模式搜索方法，Kim(1997)也提出了基于相似理论的方法。Ugai(1989)，郑颖人等(2002)，韩伟歌等(2019)，高冯等(2020)，刘康琦等(2020)等学者提出了强度折减法，通过不断增大折减系数，减小边坡材料的强度参数，直至边坡发生失稳破坏，将此时的折减系数定义为边坡的稳定安全系数。此类方法计算工作量较大，定义的稳定安全系数物理含义也不明确。

近年来，岩土力学研究者尝试了更多新方法来解决边坡稳定性分析问题。Huang et al. (1993)、杨明成等(2002)等学者提出了在有限元强度折减法或者条分法力学模型的基础上，逐段寻找最危险滑动面的局部最小安全系数法，这类分析方法在计算和收敛速度上有优越性，但无法回避强度折减法或条分法的局限性。王斌等(2017)，张巍等(2017)，刘鑫等(2019)等学者将物质点法引入边坡稳定分析中，这种方法能够很好地描述结构初始失稳破坏后的形态发展，但其计算十分复杂，无法得出意义明确的稳定安全系数。苏永华等(2019)假设滑动面为对数螺旋面，基于塑性极限分析的上限分析法构建边坡可靠度计算模型，引入响应面模型，求解得到边坡可靠度的一个上限解，其结果有一定的工程借鉴意义，但也只是陈祖煜提出的塑性边坡分析上下限原理的其一，不是准确结果。

寻找一种物理意义明确，假设条件少，计算操作简单的边坡稳定分析方法，这正是本文要研究的问题。

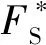
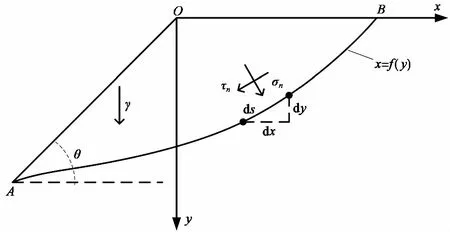
图 1 曲面上一点的法向正应力σn和切向剪应力τnFig. 1 The normal stress σn and the tangential shear stress τn at a point on the surface

本文提出的方法与经典的极限平衡法不同，计算分析过程中不需要将滑体划分成垂直条块，不需要假设滑面上的法向应力分布形式，而可以直接利用已有的坡体弹性应力解。算例表明：本文方法所得到的与简化Bishop法和有限元强度折减法获得的结果非常接近，且基本介于有限元法和简化Bishop法之间。

1 确定滑动面的原理

1.1 滑动面上的应力分布

当边坡只受到重力作用时，坡体应力场可直接通过弹性楔形体的弹性解给出(谷拴成等， 1994)：

(1)

式中：σx，σy分别为x、y向的正应力，本文规定以压为正；τxy为剪应力；γ为岩体的容重；θ为边坡的坡角。

当为平面应变问题时，AB曲面也可以理解为xOy平面内的曲线。当坡高为H时，可以求出通过坡角A的曲线x=f(y)上任一点的法向正应力σn和切向剪应力τn(图 1)：

(2)

式中：

(3)

1.2 极限平衡原理和安全系数

τn是引起坡体滑动的根源，而根据坡体材料满足的Mohr-Coulomb准则，σn所形成的内摩擦力和材料固有的黏聚力可以阻止坡体的滑动，则稳定安全系数FS的表达式为：

(4)

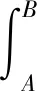
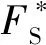
2 滑动面的参数表示

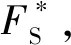
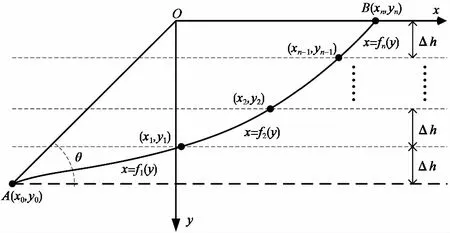
图 2 滑动面的分段表示Fig. 2 The piecewise description of sliding surface

如图 2所示，对曲面AB沿竖直方向进行等距分段，设每段曲面在竖直方向的高度都为Δh，且假定每段滑动面的形状都为一个二次多项式，当分段间隔Δh足够小时，这样描述的曲面可以反映足够多的曲面形状。需要指出的是，这里进行分段仅是为了描述滑动面形状，与经典极限平衡法对滑动体分条有本质区别。若曲面AB共被分成n段，则滑动面x=f(y)可以看作是如下的分段函数：

(5)

式中：ai，bi，ci(i=1， 2，..，n)为待定系数，式(5)中共有3n个未知系数，这3n个未知系数并不是相互独立的，根据对曲面AB的连续性和光滑性要求，可以证明只有n+1个是独立的。

曲面AB的连续性和光滑性是指分段函数在相邻两分段交界点处函数值及一阶导数值是相等的，由此通过式(5)可列出在n-1个交点处，所必须满足的2(n-1)个方程为：

(6)

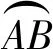
(7)

式(6)和式(7)共2n-1个方程，其中的yi(i=0， 1，..，n-1)是已知量。在这些方程中含有3n个未知系数ai，bi，ci(i=1， 2，..，n)，所以共有n+1个独立的待求未知量，本文将a1，b1，a2，a3…，an-1，an作为待求的未知量时，则由式(6)和式(7)可以求出其他未知量为：

(8)

式中：1≤i≤n-1，这样将滑动面分成n段共需要n+1个独立的未知量就可以描述整个滑动面了，变量个数的减少将更有利于最危险滑动面的优化计算。

3 最危险滑动面的搜索

3.1 计算前的理论准备

将式(3)代入式(2)可得：

(9)

式中的dx/dy=f′(y)可通过式(5)获得。式(4)可写为：

(10)

将式(1)代入式(9)，再代入式(10)便可得到计算任一曲面AB对应的FS的公式：

(11)

使用数值积分方法计算式(11)中相关积分值，将曲面AB上的每个二次曲面段沿竖直方向等距划分为m个微段，沿整个曲面共有m×n个微段，m×n+1个端点。当每个微段的长度足够小时，在每个微段上可以认为应力呈直线分布，式(11)中相关积分值可以使用梯形积分公式计算。

为了保证搜索过程中滑动面的合理性，还需要增加一些约束条件，本文仅对数值积分的分段点施加约束条件，第i个分段点的y坐标值为hi，则有

(12)

-f′(hi)>0 1≤i≤m

(13)

式(12)中，-hi/tanθ为坡面线AO上y坐标值为hi的点的x坐标值，f(hi)代表滑动面AB上y坐标值为hi的点的x坐标值，此约束条件的几何意义为限制坡体内任意深度处滑动面AB均在坡面线AO的右侧，保证滑动面上的点在边坡体的内部。式(13)中的约束条件的几何意义为保证滑动面曲线方程有单调性，防止曲线产生向坡肩方向的弯曲。

3.2 最危险滑动面的优化计算

经过上述准备之后，对最危险滑动面的搜索转化成寻找一组使稳定安全系数FS达到最小的一组系数a1，b1，a2，a3…，an-1，an，可以通过混合罚函数优化方法来实现这个过程(Fletcher， 1981； 万耀青， 1983)。

罚函数法是处理约束优化问题的一个有效方法，其基本思想是：将原问题的目标函数和约束条件按一定的方式构造出带参数的增广目标函数，把约束优化问题转化为一系列无约束优化问题来求解。按照约束形式和构造的函数及罚因子的递推方法等不同，罚函数法又分为内点罚函数法，外点罚函数法和混合罚函数法3种(Himmelblau， 1972)。内点法容易处理不等式约束优化设计问题，外点法容易处理等式约束优化设计问题，把外点法和内点法结合起来，则可同时处理既具有等式约束条件，又具有不等式约束条件的优化问题，这种方法称为混合惩罚函数法。

在本文的优化计算中，设计变量为滑动面的形状参数即X=[a1，b1，a2，a3…an-1，an]，使用的优化模型为：

(14)

式中：bi(X)>0表示不等式约束条件，可由式(11)，式(12)获得，即：

(15)

在本文的优化模型中，罚函数的形式为：

(16)

式中：r为罚因子，下标集合I1，I2定义为：

(17)

式中：X(0)为给出的原问题的计算初始点。优化过程可以通过编写的计算机程序来完成。

4 算例分析

以坡体高度为8m的土坡为例(Huang， 1993； 杨明成等， 2002)，坡体材料容重为18.5kN·m-3，并取两种不同坡率的边坡进行分析，一种是1︰1的边坡，另一种是1︰2的边坡。边坡材料的黏聚力c从2.5kPa变化到30kPa，内摩擦角φ从10°变化到20°，以考察强度参数变化对边坡稳定性的影响。对每一种情况，分别用本文方法，郑颖人等(2002)中的有限元方法和边坡设计中常用而且我国《公路路基设计规范》推荐的简化Bishop法确定临界滑动面并计算最小稳定安全系数，计算结果见表 1。

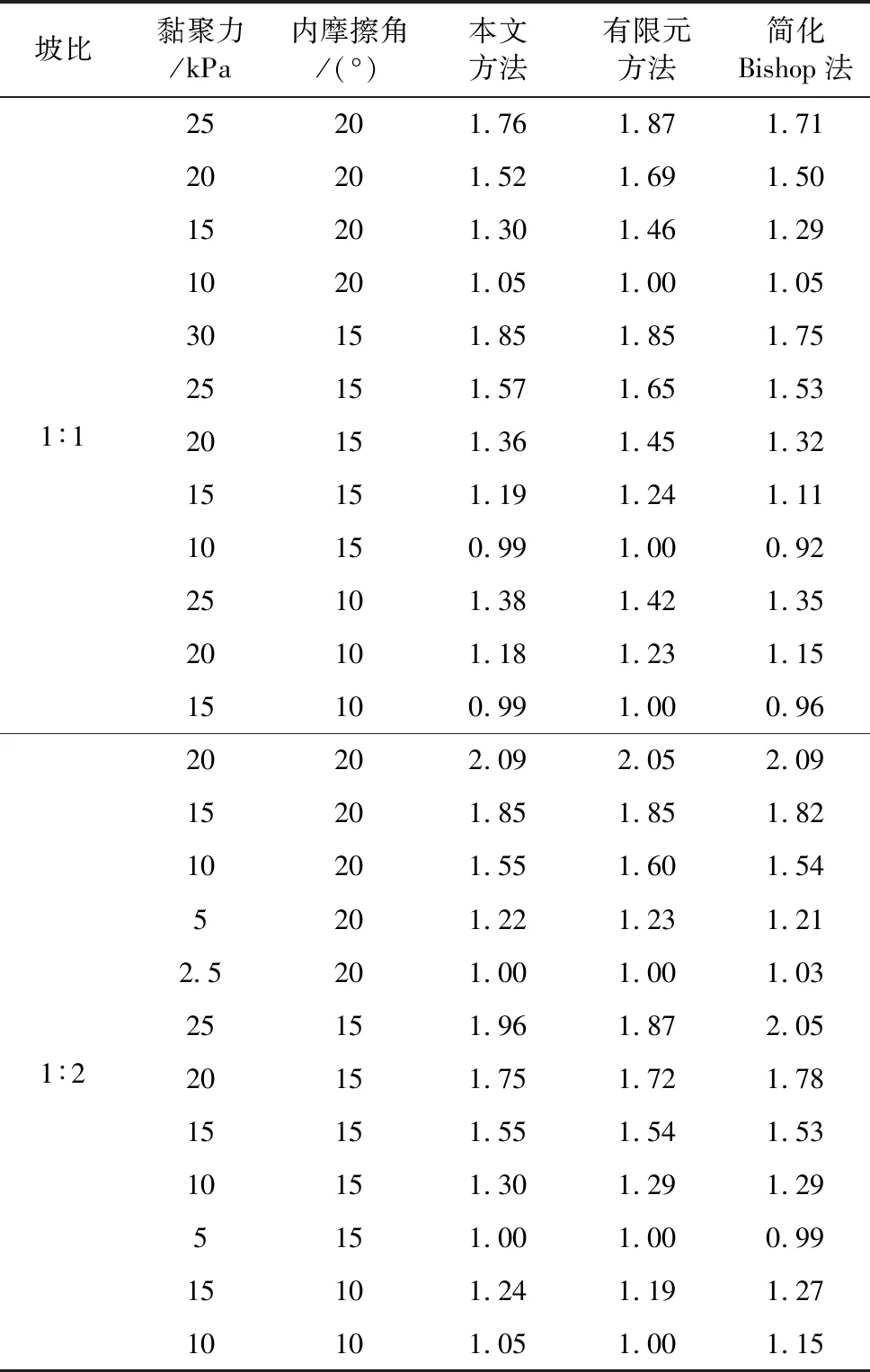
表 1 不同分析方法所获得的稳定安全系数Table 1 Factor of safety obtained by different methods

表中，本文方法取m=100，n=10计算。简化Bishop法对应的整体最小稳定安全系数由文献《土坡稳定分析》(黄仰贤，1988)的稳定图表给出，这种方法假设滑动面为圆弧面，认为条块间竖直方向的剪力为零，条块间只存在水平方向的作用力，通过不同圆弧面的圆心和半径组合试算寻找最危险滑动面。有限元法对应的整体最小稳定安全系数使用局部最小安全系数法(Huang et al.,1993)得到，该法使用基于准则的有限元方法求解边坡体的有效应力状态， 然后使用莫尔-库仑准则估算坡体内一点处的剪切强度s，根据莫尔圆计算剪应力τ，并定义局部安全系数为FSL=s/τ，通过强度折减，认为局部稳定安全系数小于或等于1的点为破坏点，将这些破坏点连接起来，就得到临界滑动面，而强度折减系数就是所要求的最小稳定安全系数。

从表 1可见，边坡的稳定安全系数随着坡体材料内摩擦角φ和黏聚力c的增大而增大。3种方法获得的稳定系数相差很小。当坡比为1︰1时，在12个算例中，基本上有这样的规律：有限元法获得的稳定安全系数最大，简化Bishop法获得的稳定安全系数最小，而本文方法介于两者之间； 而当坡比为1︰2时，获得的规律与坡比为1︰1时获得的规律完全不同，在12个算例中，除了相等的稳定安全系数之外，简化Bishop法获得的稳定安全系数有5个为最大，有限元法和本文方法获得的稳定安全系数各有2个为最大。综上所述，本文方法获得的稳定安全系数基本介于有限元法和简化Bishop法之间。

图 3和图 4给出了1︰1的边坡，两种内摩擦角和黏聚力情形下，3种方法确定的最可能滑动面形状。

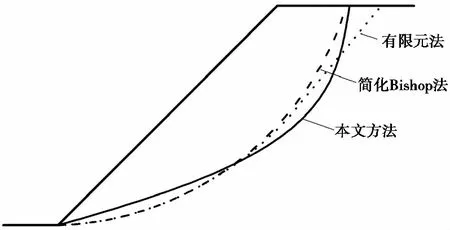
图 3 1︰1边坡的最可能滑动面(c=10kPa，φ=15°)Fig. 3 The most dangerous sliding surface in 1︰1 slope(c=10kPa，φ=15°)

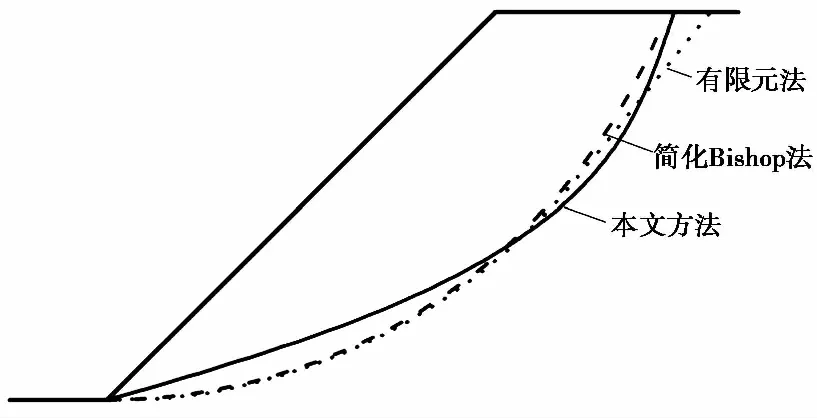
图 4 1︰1边坡的最可能滑动面(c=15kPa，φ=10°)Fig. 4 The most dangerous sliding surface in 1︰1 slope(c=15kPa，φ=10°)

5 结 论

对于岩质或土质边坡，只要其材料组成大致均匀，就可以简化成均质的楔形弹性体，若坡体只受到重力作用，则可利用弹性力学的逆解法，求出坡体的各个应力分量。本文基于坡体为库仑材料的假定，提出了一种任意滑动面的均质边坡滑动稳定分析的极限平衡方法，该方法具有以下特点：

(1)物理意义比较明确，假设条件较少，在求解过程中也不存在数值计算上的困难。

(2)通过算例分析表明，本文方法所得到的边坡稳定安全系数与简化的Bishop法和有限元强度折减法的结果非常接近，且基本介于有限元法和简化Bishop法之间。

(3)计算得到的最危险滑动面可以反映上陡下缓的特点，滑动面是向上凹的光滑曲线，且在坡顶的形状与实际情形更加接近，可以很好地解释坡顶所出现的陡峭裂缝。

当坡体的材料组成不均匀，甚至有多层土以及某些软弱土层时，难以求出应力的解析解，但可以利用有限元等数值方法求出坡体内的应力，再利用本文对滑动面形状的处理方式，便可解决这种复杂情形下的坡体稳定分析问题。